盾构切削混凝土刮刀受力和磨损的离散元数值模拟研究

刘浩 ，许宇 ，李兴高 ，杨益

（1.北京交通大学 交通运输学院，北京 100044；2.北京交通大学 土木建筑工程学院，北京 100044；3.中铁第一勘察设计院集团有限公司，陕西 西安 710043；4.济南轨道交通集团有限公司，山东 济南 250014）

随着城市人口的增加，城市中心区各种建（构）筑物越来越密集，使用盾构法修建地铁隧道时难以避免地会切削各种建（构）筑物的桩基［1］，如苏州轨道交通2号线切削广济桥桩基、广州地铁3号线切削居民楼桩基、上海轨道交通10 号线切削沙泾港桥桩基等，这些切削穿越对盾构机刀具性能提出了更高要求.混凝土桩基中的钢筋一般采用滚刀或专门设计的先行撕裂刀来切削［2］，而刮刀作为软土盾构机使用最为广泛的刀具，则不可避免地需要承担切削范围更大的混凝土的任务.一般而言，盾构刮刀主要适用于土和软岩的切削，用来切削强度较高的混凝土，存在切削能力不足、刀具破损严重导致使用寿命大大降低的问题.同时，刀具切削能力不足易引起螺旋输送机排渣不畅等问题［3］.因此，有必要研究盾构刮刀切削混凝土过程中的受力，为刮刀参数设计和磨损性能评价提供依据和理论支持.

数值模拟方法具有成本低廉、重复性强等优点，且易于实现复杂工作场景的再现，在刀具切削作用研究中得到了广泛的应用.其中，离散元法把研究对象看成颗粒集合体，颗粒运动满足牛顿第二定律，颗粒间的相互作用力通过接触模型来描述，材料的破坏理解为颗粒间相互作用力的丧失，有效规避了有限元法求解大变形时的网格畸变问题，尤其适用于模拟岩土材料在准静态或动态条件下的变形及破坏过程.起初，离散元法被用于农耕刀具的切削作业模拟，Su 等［4］利用PFC3D 软件模拟了刀具切削不同强度颗粒所需要的最大切削力.Ucgul 等［5］在离散元软件DEM 中采用滞回弹簧接触模型，探讨了旋耕刀在砂土中的拉力与刀具前角、刀具与地面之间夹角等多种因素的关系.Helmons 等［6］将离散元与环境流体渗透相耦合，论证了在DEM 中引入光滑颗粒空隙压力法来模拟饱和岩体切削的准确性.后来，离散元被广泛用于研究盾构滚刀破岩机理，Moon 等［7］采用离散元软件DEM 分析了滚刀切削完整岩体的过程，研究了刀具间贯比（间距与切削深度的比值）对其受力的影响.杨开新等［8］将考虑胶结尺寸的微观接触模型植入离散元软件PFC2D 中，模拟了4 种岩性下不同滚刀刃数的破岩过程，探究了岩性、滚刀刃数对破岩效率的影响.徐琛等［9］采用有限差分法和离散元法相耦合的数值模拟方法，对不同刀间距和贯入度条件下TBM 双滚刀破岩过程进行了三维动态仿真，分析研究了不同滚刀配置对岩石破碎效果的影响.近年来，盾构切刀的破岩过程越来越受到关注，Rojek 等［10］分别采用离散元二维和三维颗粒模型模拟了切刀的破岩过程.谭青等［11］采用离散元软件PFC2D 建立了岩石和刀具的二维数值模型，并利用自制的浆试件对刀具切削参数进行了研究.张旭辉等［12］利用离散元软件PFC2D进行了软岩与盾构切刀的二维数值模拟，并结合切削试验证明了离散元数值模拟结果的准确性.

总的看来，在岩土体刀具切削方面的研究，目前大多集中于滚刀破岩方面，刮刀切削的研究大多是以农耕刀具和金属切削的研究为出发点，针对混凝土切削的成果较少.现有的刮刀切削混凝土的研究多简化为二维模型，且轨迹均为直线，但考虑到真实的桩基弧面，二维的直线切削与实际情况存在明显差异.因此，本文在刀具弧形轨迹切削混凝土室内试验的基础上，利用离散元软件EDEM，研究了刀具在切削不同强度试件时其受力与刀具前角、刀具后角、切削速度和切削深度等参数的关系，并基于Archard模型探讨了刀具的磨损情况.

1 刮刀弧形切削混凝土数值模型

1.1 建模依据

本文以文献［13］详细介绍的刀具弧形切削混凝土的模型试验为依据建立数值模型.图1 为试验中采用的刀具弧形切削混凝土试验平台，依靠图1 中所示千斤顶的配合动作，实现刀具对混凝土试件的弧形切削，更加符合工程中刮刀切削桩基弧形面的实际情况.试验中用到了强度分别为M2.5、M5、M7.5和M15 的四组试件，试件尺寸统一为200 mm×200 mm×200 mm.对各组水泥砂浆试件单轴抗压强度进行了测试，测试结果见表1.试验共制作了7 把刀具，刀具材料为45 号钢，与实际工程中的刮刀主体材料强度基本一致，但简化了刀头的硬质合金.试验测试刀具前角、刀具后角和刀刃形状3 个因素对切削力的影响.刀具参数如表2和图2所示.利用图1所示试验平台，全面测试分析了刀具前角、刀具后角、刀具形状、试件强度、切削深度和切削速度等对刀具法向切削力和切向切削力的影响.试验结果为本文建立的离散元模型提供了充分的建模和验证依据.

图1 刀具切削混凝土试验平台Fig.1 Test device of concrete-cutting by scrappers

图2 试验切刀的几何参数Fig.2 Geometrical parameters of the test scrappers

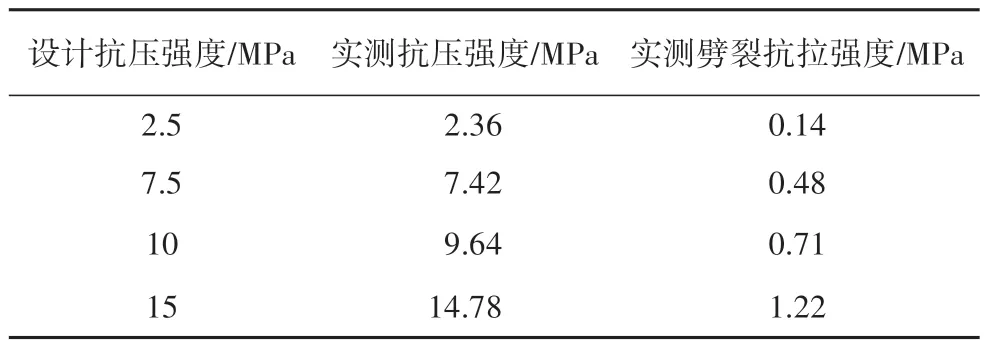
表1 采用的混凝土试件强度Tab.1 Strength of the used concrete samples

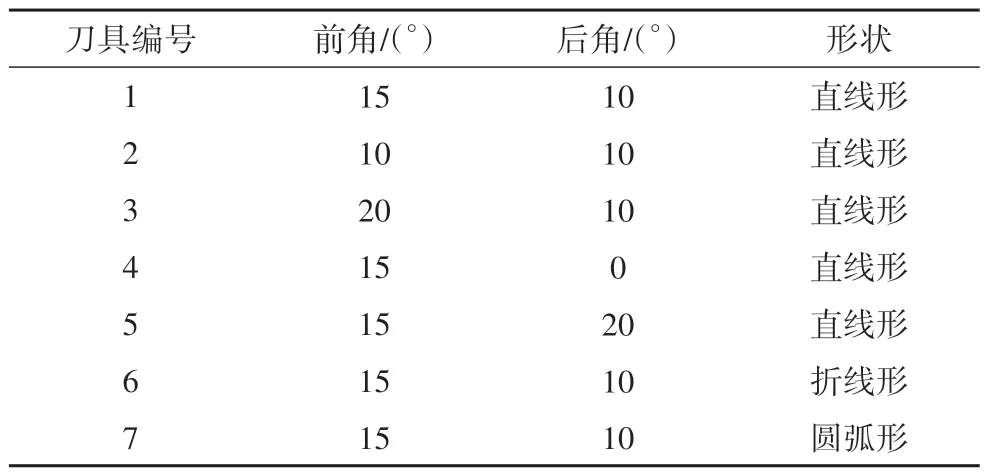
表2 试验切刀参数Tab.2 Parameters of the test scrappers

1.2 参数标定

混凝土试件在离散元中可看成由无数离散的颗粒互相黏结而成，刀具切削就是将颗粒剥离试件母体的过程.如图3 所示，本文采用离散元软件中的bonding模型，将77 824个直径为5 mm的颗粒黏结成200 mm×200 mm×200 mm 试件.通过两个虚拟标定试验（单轴压缩和劈裂抗拉）对试件中颗粒之间的黏结键参数进行了标定，反复尝试后，得到表3 所示颗粒参数值.将模拟所得的单轴压缩和劈裂抗拉强度值与室内试验所测的单轴压缩和劈裂抗拉强度值进行对比及误差分析，如表4 所示.可以看出，模拟的抗压强度和抗拉强度均与实际测试强度值误差保持在17%以内.

表3 不同强度试件的参数值Tab.3 Parameters for test samples of different strengths

图3 混凝土试件离散元模型Fig.3 Discrete element model of concrete sample

1.3 接触模型

在数值模拟单轴压缩试验、劈裂抗拉试验及刀具切削试验时，采用了EDEM 软件自带的三个计算模型［14］：Hertz-Mindlin（no slip）模型、Hertz-Mindlin with Bonding 模型和Archard Wear 模型，其中Hertz-Mindlin（no slip）模型是EDEM 中最常用的颗粒与颗粒或者颗粒与几何体的接触模型，其仅考虑了切向力和法向力，且无黏结作用；Hertz-Mindlin with Bonding 模型适用于模拟破碎、断裂等问题；Archard Wear 模型则是几何体的磨损模型.为节约计算成本，本文在模拟时设定一个时刻tBOND，tBOND代表混凝土试件的成型时刻，在tBOND时刻前对颗粒使用Hertz-Mindlin（no slip）模型以完成颗粒生成、试样成型等一系列工作.在tBOND时刻，将Hertz-Mindlin（no slip）模型替换为Hertz-Mindlin with Bonding 接触模型，同时开启Archard Wear 模型，此时颗粒之间便产生了黏结力，其可以模拟具有一定强度的混凝土试件，即可开始刮刀切削作业.

1.4 切削试验仿真

将SolidWorks 中的刀具三维模型导入EDEM中，并在固定试件的位置产生bonding 颗粒，颗粒参数按照标定试验结果进行设置.为在后处理中得到更直观的刀具受力云图，将SolidWorks 中建立的刀具三维图导入软件hypermesh 中进行网格划分，如图4 所示.将划分网格后的刀具调整至对应的切削深度，再以其支座为圆心，给下方千斤顶赋予旋转角速度（切削速度），使刀具对试件进行切削.

图4 网格化的刀具Fig.4 Meshed tools

在此说明，室内试验中刀具的真实切削速度是一个变量，如上部油缸在8 mm/s、16 mm/s 和32 mm/s速度下进行切削时，其真实刀具切削速度为油缸速度的1.60～1.71 倍，分 别为12.8～13.68 mm/s、25.6～27.36 mm/s 和51.2～54.72 mm/s.而在软件EDEM 中只能设定刀具以固定角速度进行切削，由于每次切削刀具线速度变化不大，因此认为在EDEM 刀具的切削速度恒定，取中间值为13.1 mm/s、26.2 mm/s 和53.0 mm/s，即设定刀具角速度近似为1°/s、2°/s 和4°/s.针对不同刀具前角和后角、不同切削速度和不同试件强度的刀具切削进行了模拟仿真.

1.5 模型验证

1.5.1 切削力验证

以刀具（前角15°、后角10°、直线形刀尖）在1°/s的角速度和10 mm 的初始切削深度条件下切削强度为7.5 MPa 的试件的模拟情况为例，将数值模拟结果与试验切削机得到的结果进行对比分析.由于刀具切削试验只能获得法向切削力和切向切削力两个数据，在此仅对比分析此两类数据，具体如图5 所示.可以看出，离散元数值模拟得到的切削力结果较切削试验得到的结果有更大的波动性，其原因是由于切削机采集数据频率有限，采样间隔为0.3 s，而数值模拟采样间隔设置为0.1 s，故而模拟数据波动较试验数据波动更大，但数值模拟和试验两者的刀具受力均值均维持在同一条水平线，其中法向力均在10 000 N 上下波动，切向切削力在5 000 N 上下波动，在不计数据波动的前提下，可认为离散元数值模拟在刀具切削混凝土方面具有较好的准确性.同时，在刀具刚刚接触试件时，由于刀具与试件的碰撞作用，受力较大，之后的切削力在一定范围内波动；13 s 往后的刀具受力突然降低到0 附近，这是由于在刀具即将完成切削时，会将试件最后部分从底部临空面整体剥落，致使切削力骤减，此效果在切削试验和数值模拟中均有表现，如图6 所示，表明离散元数值模型能真实反映盾构切刀的切削行为.

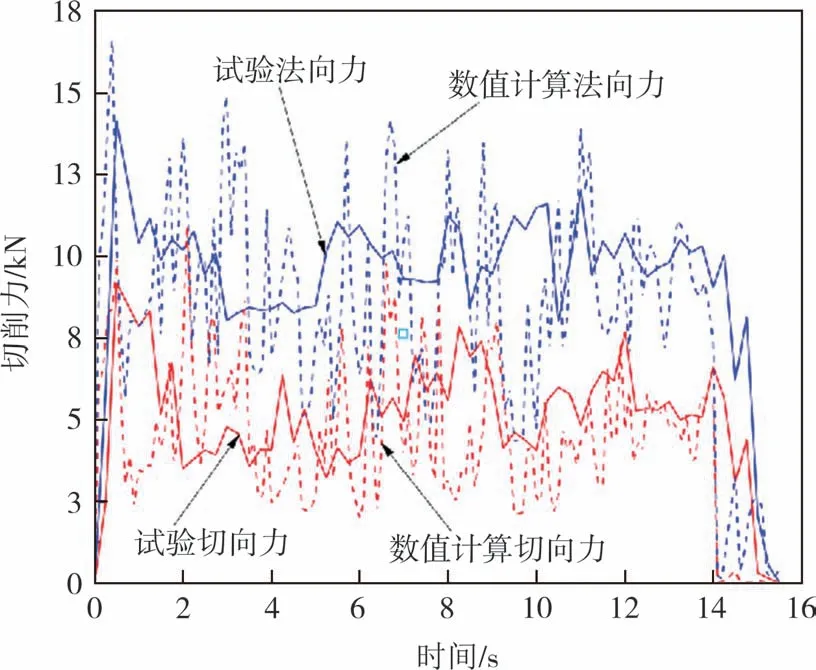
图5 数值模拟和试验所测切削力对比Fig.5 Comparison of the cutting force by numerical simulation and measured in tests

图6 试件底部的整块剥落现象Fig.6 Peeling phenomenon at the bottom of the test block

1.5.2 材料破坏及刀具损伤验证

根据上述算例结果，进一步验证切削过程中材料破坏和刀尖受力情况.在数值模型试件中部沿刀具切削方向取40 mm 厚的薄层，输出薄层中颗粒间的黏结键状态，如图7所示.由图7可知，在被切削过程中，只有与刀具接触处的试件颗粒在运动，且碎屑以块体为主，黏结键在刀尖的行程前方提前断裂，而其他未与刀具接触的颗粒基本未受影响.

图7 切削时颗粒黏结键变化Fig.7 Change of the particle bonding keys when cutting

图8 为切削前和切削时的颗粒速度图.可以看出，切削后的碎屑颗粒基本均沿着刀具的前角面移动，其余部分几乎不动.在EDEM 后处理中输出切削全程中刀具单元受力矢量的时间平均值，将其耦合到有限元软件ANSYS Workbench 中得到刀具受力云图，如图9（a）所示.由图可知刀具切削试件时其前后侧三面交汇的棱角点处受力最大，前后角面交汇的刀尖处受力次之，且刀尖直线部位受力不均匀，而刀具其他位置几乎不受力.

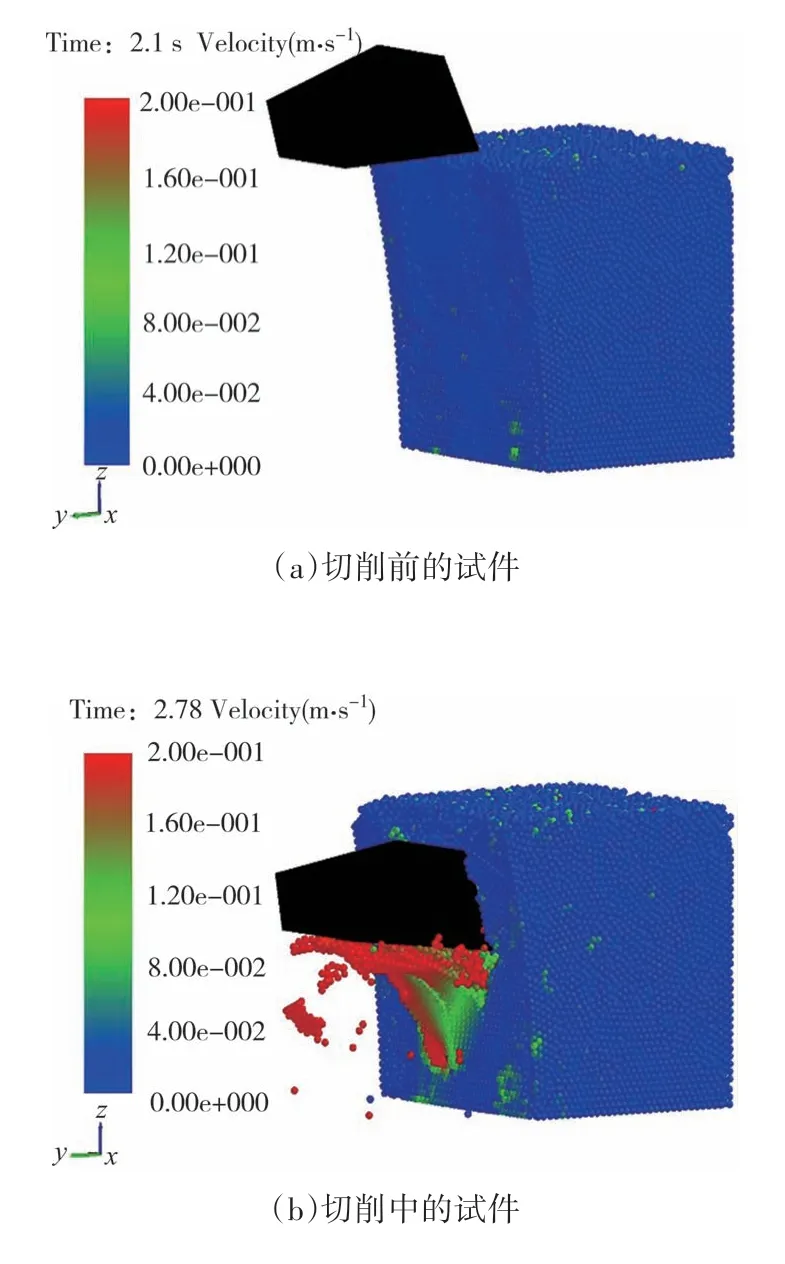
图8 切削的三维模拟图Fig.8 The cutting 3D simulation

在Workbench 中对刀具的4 个螺栓位置进行约束，并输入离散元中刀具的受力数据进行加载，得到的刀具变形如图9（b）所示，可以看到刀具前后侧三面交汇处变形最大，刀尖处次之.

周辰等［15］、熊文亮等［16］的研究表明，切削刀具的刀尖位置易发生崩刃.图9（c）为室内试验后的刀具崩刃图，可以发现刀尖位置磨损较大且在顶点位置发生崩刃行为.这与图9（a）和（b）所示刀具受力及变形结果十分吻合，说明数值计算结果与试验结果表现出良好的一致性.

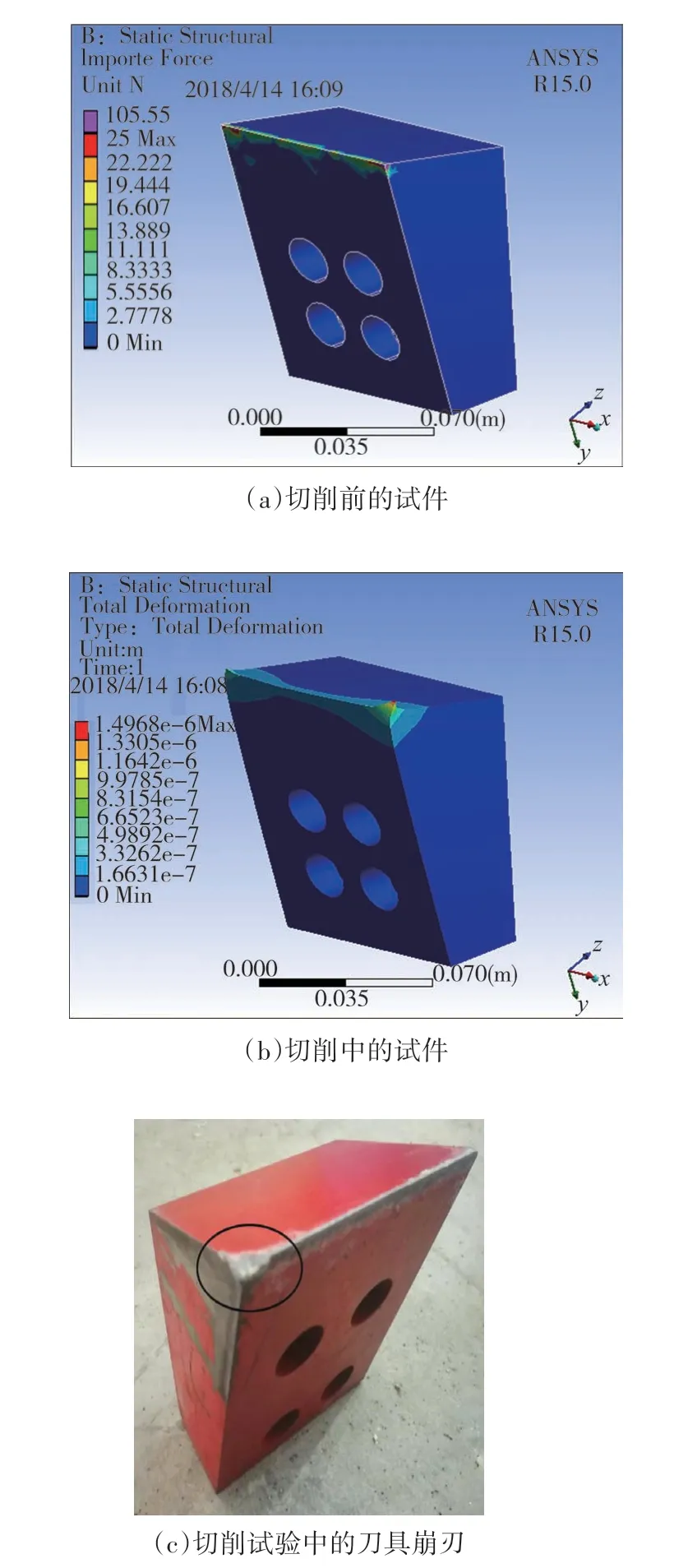
图9 刀具受力分析Fig.9 Force analysis of the scrappers

取离散元中4.1 s、4.3 s、4.5 s 和4.7 s 时的刀具瞬时受力数据，将其耦合到Workbench 中，查看刀具三维受力，如图10所示.由图10可知，切削过程中刀具受力不均匀且随时间来回波动，刀具的受力位置及大小变化极快，且每个瞬时刀尖仅个别单元承受绝大部分切削力，由此导致了刮刀崩刃.

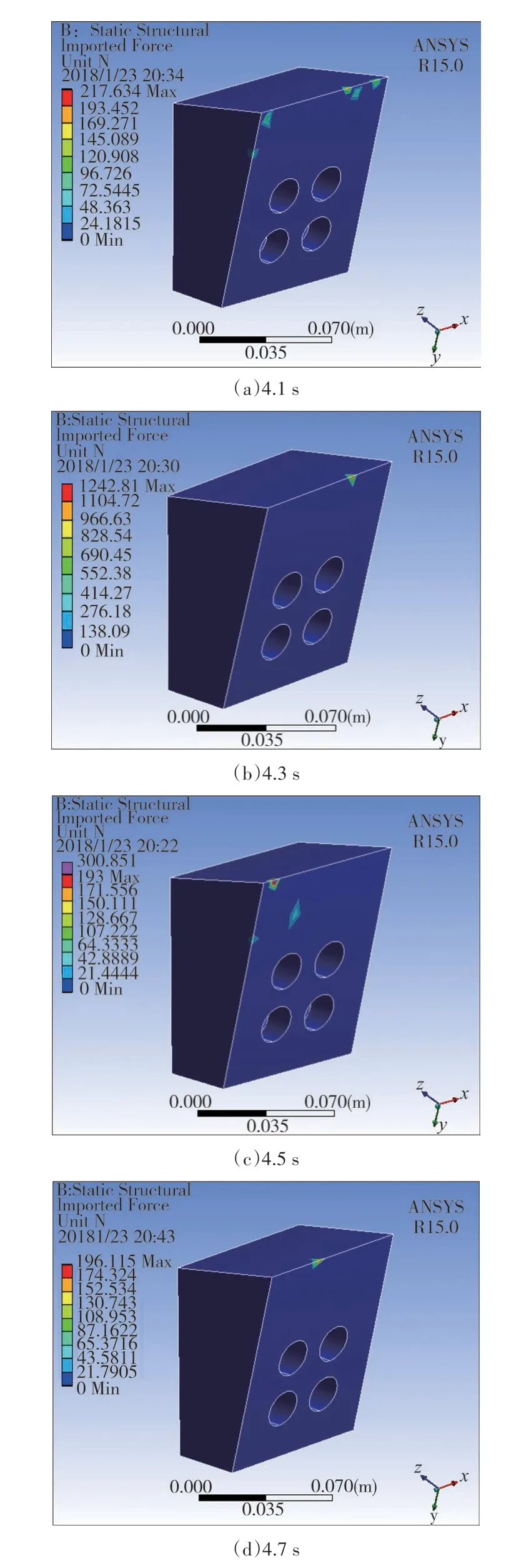
图10 刀具瞬时受力三维云图Fig.10 Three-dimensional nephogram of the forces on scrap-pers

2 不同计算方案下的刀具受力

表5列出了不同刀具参数（前角为10°、15°、20°，后角为0°、10°、20°，刀尖形状为直线形、折线形、圆弧形）、不同刀具切削速度（1°/s、2°/s、4°/s）、不同初始切削深度（5 mm、10 mm、15 mm、20 mm）条件下切削不同强度（2.58 MPa、7.51 MPa、9.80 MPa、14.16 MPa）试件时的计算方案，其中初始切削深度是指刮刀与试块初次接触时的切削深度.不同计算方案下切削力平均值、试验测试值以及刀具切向力和法向力误差如表6 所示.其中，法向力和切向力的误差定义为计算值与试验值的绝对差值与试验值的比值；力比值定义为计算法向力与计算切向力之比.可以看出，和试验结果相比，离散元模拟得到的切削力均值除了在切削速度为2°/s和4°/s时的误差大于10%外，其余误差均在10%以内.可能的原因为：一是由于试验中的刀具在切削速度较大时发生磨损较大，易造成刀尖变钝，切削力随之增大，而数值模拟中的刀具假定不发生损耗；二是由于当试验中的切削速度过大时，在侧向力的作用下，刀具会发生较大的侧向位移，而数值模拟中的刀具轨迹稳定，由此导致两者数据误差较大.表6 中力比值的计算结果为1.6～2.0，且以2.0 居多，说明刮刀切削过程中法向受力较大，约为切向力的2倍.

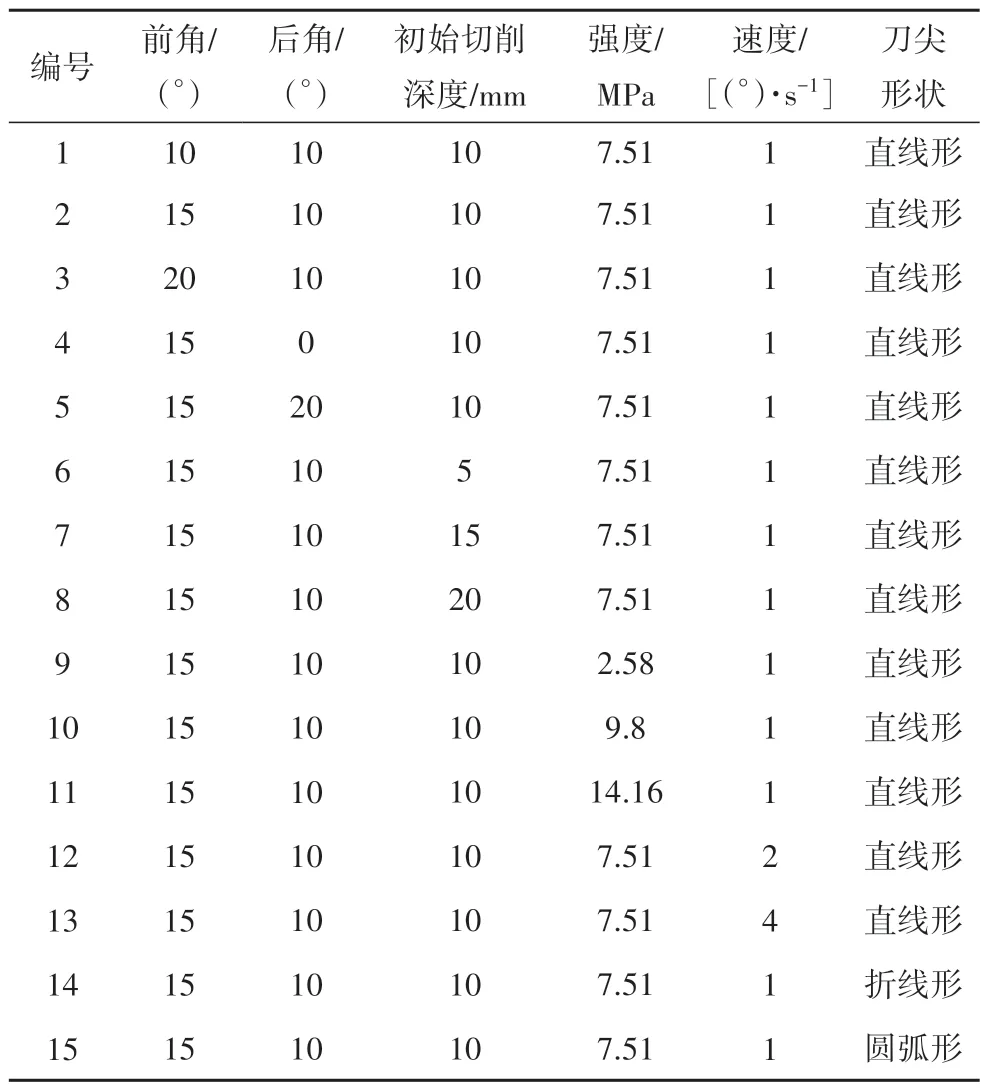
表5 计算方案Fig.5 Computation scheme

综合表5和表6，对比计算方案1、2、3可以看出，刀具前角越大，即刀尖越锋利，刀具受力越小；对比方案4、2、5 可以看出，后角增大时，刀具受力先增大再减少，后角改变对刀具受力的影响幅度较小；对比方案2、14、15 可以看出，不同刀尖形状下的刀具受力差值较小；对比方案9、2、10、11 可以看出，试件的强度越大，刀具受力越大；对比方案6、2、7、8 可以看出，刀具切削力随刀具的切削深度增大而增大；对比方案2、12、13可以看出，刀具切削速度越大，刀具受力越大.

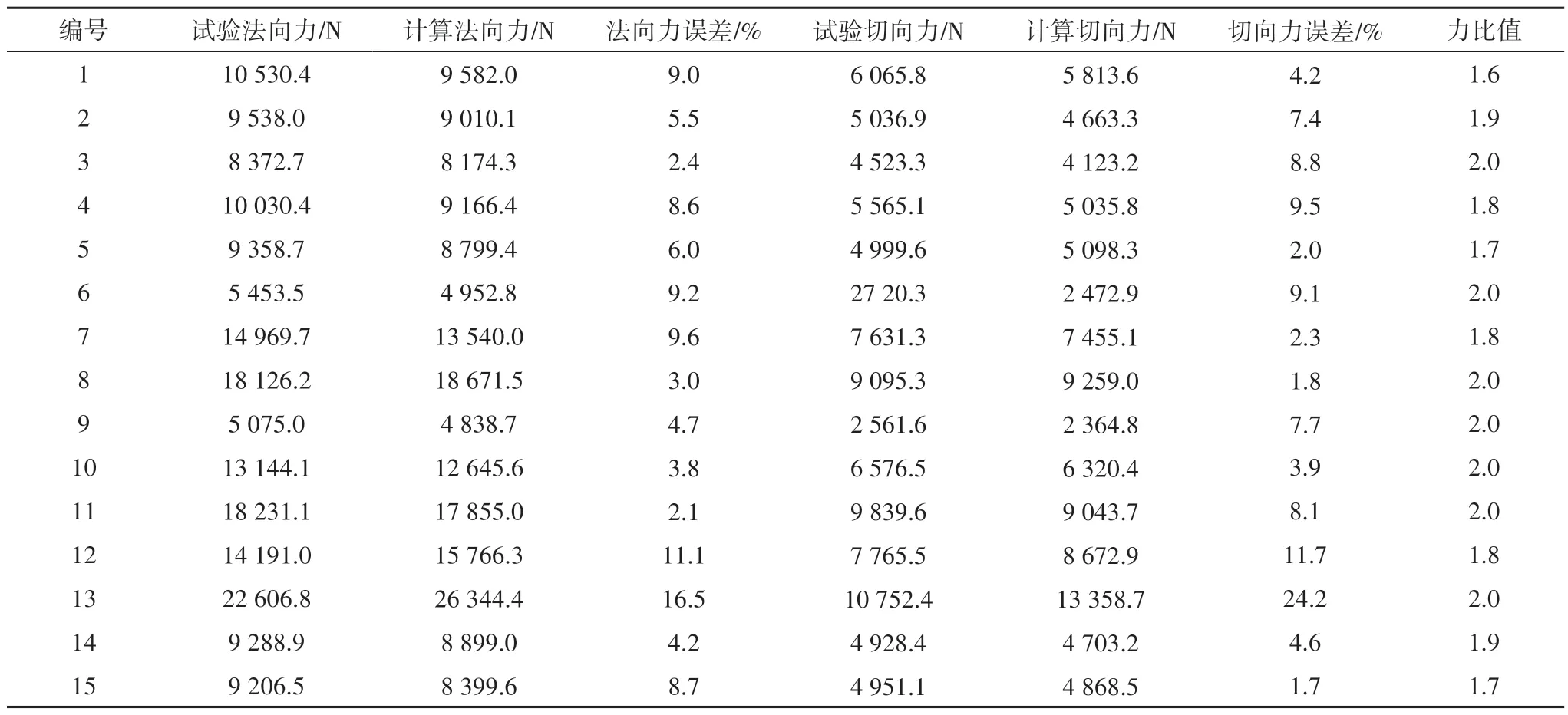
表6 计算结果与室内试验结果的对比Tab.6 Comparison between computation results and test results

3 不同计算方案下的刀具磨损

刀具磨损计算中颗粒与刀具接触采用Archard模型计算刀具所产生的磨损消耗量.根据Archard 黏着磨损定律，磨损体积与载荷和滑动距离成正比，而与磨损表面的硬度成反比，其中载荷和滑动距离可由数值模型精确计算，经验证模拟中刀具受力载荷与试验结果基本一致.但考虑到实际工程中采用刮刀的材质参差不齐，刀头通常采用合金材料，因此刮刀材料的表面硬度较难确定［17］.为简化分析，本文未对模型颗粒与刀具间的磨损系数K进行参数标定，仅是假定其为1×10-13/Pa，定性探讨刀具磨损量与刀具前后角、切削速度、试件强度等的关系及发展趋势.

3.1 刀具切削过程中的磨损量变化

对刀具1 在4°/s 的角速度和10 mm 的切削深度条件下切削7.5 MPa试件的模拟进行分析，截取计算模型切削过程中在3.5 s、7 s、10.5 s 和14 s 不同时刻的磨损云图，如图11所示.其中Archard Wear表示面网格的法向磨损深度，单位为mm，即磨损体积与网格面积之比.

如图11 所示，磨损最早发生在前后面交汇的棱角处，且该处磨损最为严重，同时刀具前角面磨损量要大于后角面，侧面磨损量最小.分析原因如下：

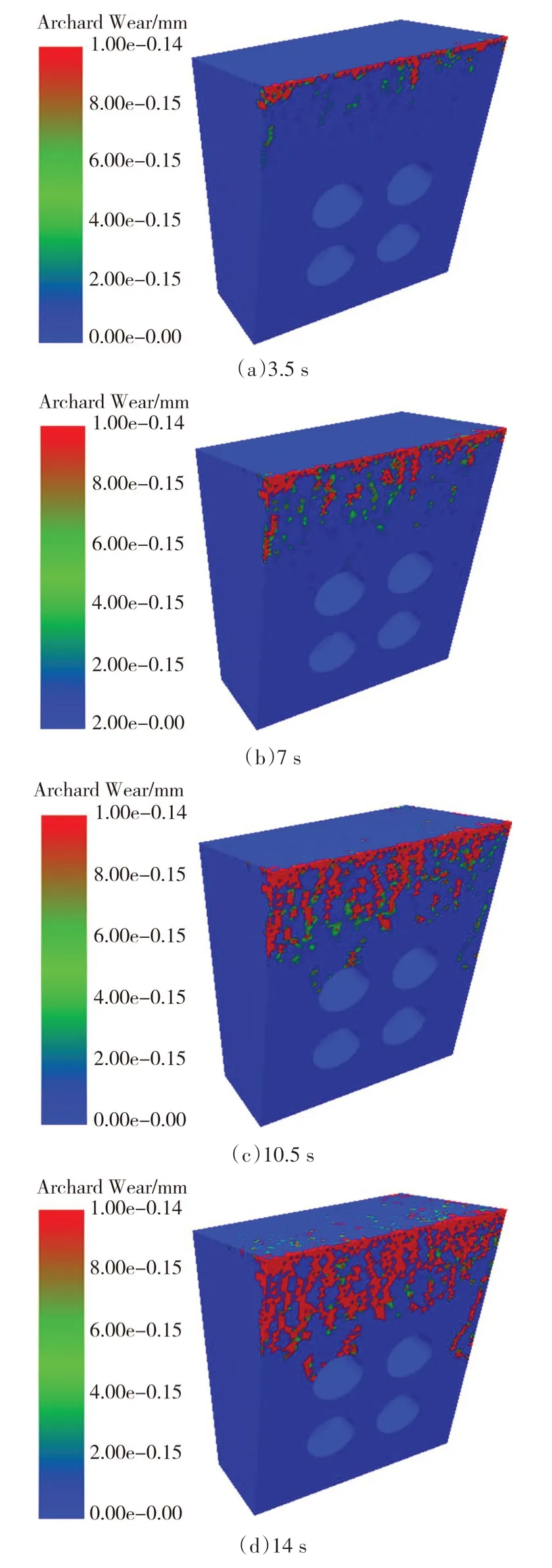
图11 刀具磨损云图Fig.11 Nephogram of the scrappers

1）切削主要靠刀尖处与试件进行接触，此处受力最大，从而磨损发生最早且最为严重；

2）切削后的碎屑从前角面滑动离开，二者接触仅仅是重力与摩擦力的作用，相对于刀尖处的碎屑所受外力较小，而后角面除离刀尖较近的部分外，其他部位基本与试件无接触，因此刀尖处磨损量大于前角面磨损量，前角面磨损量大于后角面磨损量；

3）由于刀具侧面与试件的接触面积主要取决于切削深度的大小，而切削深度与刀具长度相比较小，且侧面受力也最小，因此刀具侧面磨损量仅仅发生在刀尖处的一小部分，在三个接触面中最小.针对刀尖处较大磨损的实际，在工程中常常在刀尖处加入硬质合金来延长刀具使用寿命.

3.2 刀具形式对最大磨损量的影响

图12 给出了计算方案1、2、3（刀具前角10°、15°和20°）刀具最大磨损量随时间的变化.可以看出，刀具在刚接触试件的0.2 s内，发生了较大磨损，这是由于刀具与试件在初始接触阶段发生了碰撞作用，且碰撞力较大，从而引起磨损量较大增长；随后磨损速度随时间增长较为均衡，且前角越大，磨损速率越大.由图可知，总磨损量大致与前角度数成正比，比例系数在（2.0～2.4）×10-9mm/［（°）·s］范围内.从磨损控制的角度而言，刀具“钝”些较好.

图13 给出了计算方案4、2、5（刀具后角0°、10°和20°）刀具最大磨损量随时间的变化.可以看出，刀具后角为20°时其最终磨损量最大，10°次之，0°最小，这说明在刀具不发生损耗的假设前提下，刀具后角越大，刀尖越锋利，则其磨损量越大.与图12 中的计算结果相比可知，前角变化对最终磨损量的影响比后角大.

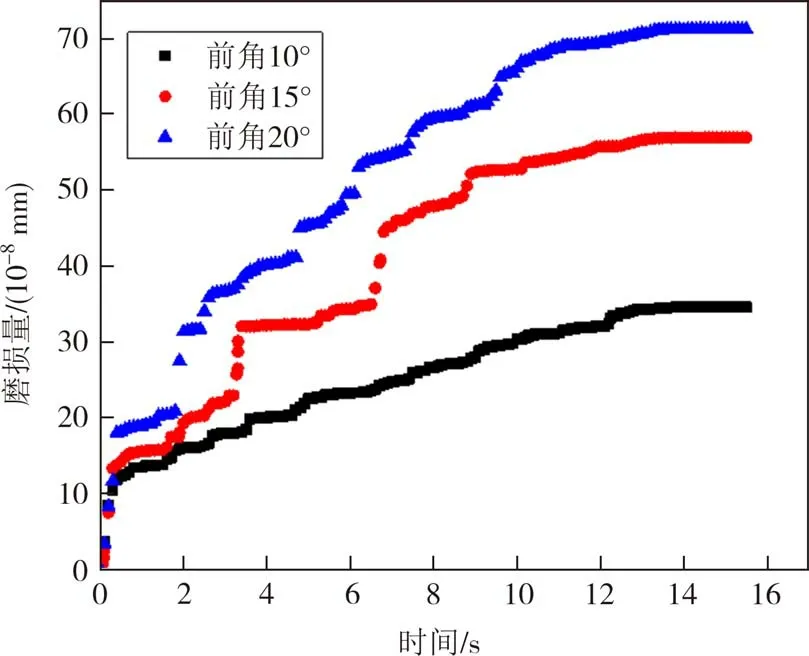
图12 刀具前角组磨损量变化Fig.12 Wear amount changes of the scrappers with different rake angles

图13 刀具后角组磨损量变化Fig.13 Wear amount changes of the scrapperswith different relief angles

图14 给出了计算方案2、14、15（刀尖形状为直线形、折线形和圆弧形）刀具最大磨损量随时间的变化.可以看出，折线形刀具的磨损最为严重，直线形次之，圆弧形最轻.原因为折线形刀具的刀尖棱位置有三个棱角，而直线形和圆弧形刀具仅有两个棱角，且直线形刀具的刀尖棱角较圆弧形刀具的棱角更尖锐.当刀尖棱角越多且尖锐时，磨损量越大.虽然圆弧形刀具磨损量最小，但由于加工相对困难，因此在实际工程中一般选取直线形刀具.

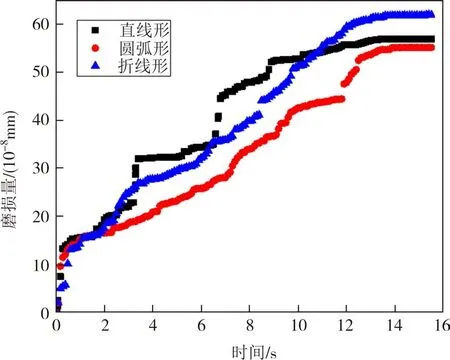
图14 刀具形状组磨损量变化Fig.14 Wear amount changes of the scrappers with different cutter tip shapes

图15 给出了计算方案9、2、10、11（试件强度为2.58 MPa、7.51 MPa、9.80 MPa和14.16 MPa）刀具最大磨损量随时间的变化.可以看出，试件强度越大，刀具磨损量增长越快.这是由于试件强度越大，刀具承受的切削力就越大，刀具磨损量也随之增加.

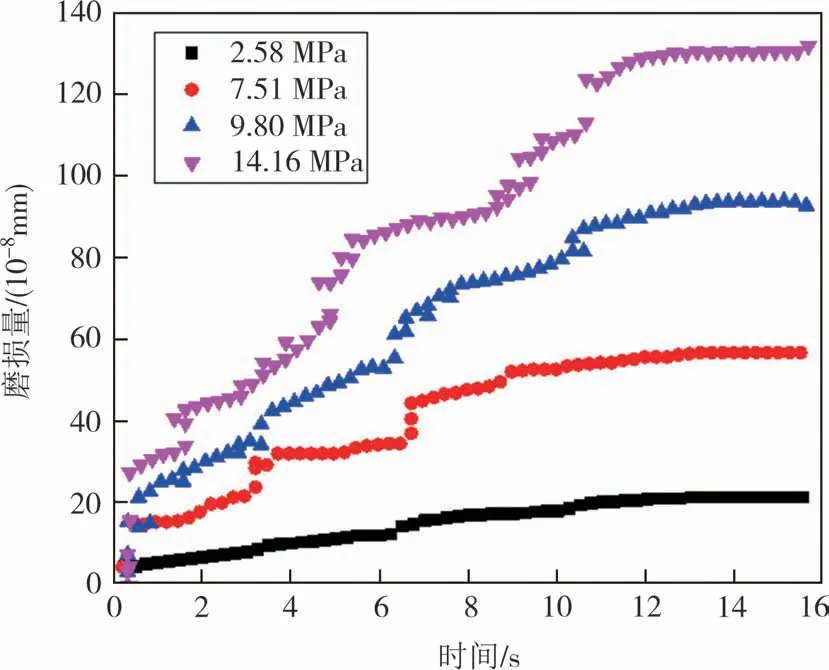
图15 刀具切削试件强度组磨损量变化Fig.15 Wear amount changes of the scrappers cutting samples with different strength

图16 给出了计算方案6、2、7、8（刀具初始切削深度5 mm、10 mm、15 mm 和20 mm）刀具最大磨损量随时间的变化.可以看出，刀具的切削深度越大，其对应的磨损量越大，且切削深度越大，在刀具与试件接触的初始阶段，磨损量增长越快.初始切削深度5 mm 时刀具总磨损量约为4×10-7mm，初始切削深度10 mm 时刀具总磨损量约为5.5×10-7mm，初始切削深度为15 mm 时刀具总磨损量约为6.8×10-7mm，初始切削深度为20 mm 时刀具总磨损量大约为7.8×10-7mm.可以看出，初始切削深度每增加一倍，刀具磨损量大致增加了50%左右.

图16 切削深度组刀具磨损量变化Fig.16 Wear amount changes of the scrappers under different cutting depth

图17 给出了计算方案2、12、13（刀具切削速度为1°/s、2°/s 和4°/s）刀具最大磨损量随时间的变化.可以看出，切削速度越快，刀具的磨损量越大，且在初始0.2 s 内磨损量增加最快.其原因为，刀具切削速度越快，与试件之间的碰撞作用越明显，两者之间的作用力则越大，因此在切削距离相同时，切削速度越快，刀具磨损则越多.

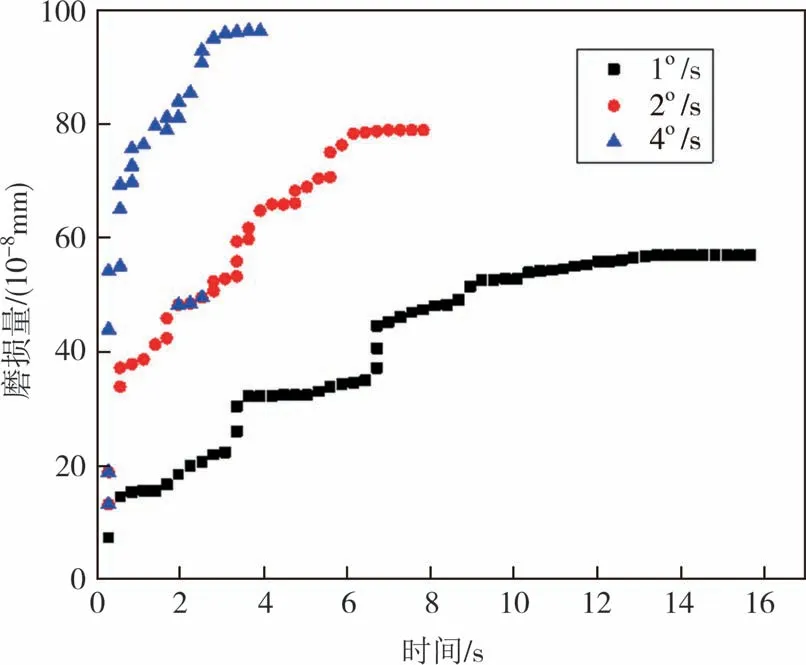
图17 切削速度组刀具磨损量变化Fig.17 Wear amount changes of the scrappers with different cutting speed

4 结 论

1）采用离散元软件EDEM 中bonding 模型模拟混凝土试件，利用单轴压缩和劈裂拉伸数值试验标定计算模型参数，数值计算得到的刀具受力和变化规律与室内试验测得的结果基本一致，其中单把刮刀的法向力在10 000 N左右，切向力在5 000 N左右，证明了离散元法在模拟刮刀切削混凝土方面的合理性和有效性.

2）数值计算表明，切削混凝土时刮刀受力是动态变化过程.在刀具与试件初始接触时，由于碰撞作用，刀具受力较大；随后刀具受力在某个固定值附近波动；在切削即将完成时，刀具往往会因试件整块剥落，受力骤降至0.刀具法向受力约为其切向受力的2 倍左右.刀具切削时的主要受力部位为刀尖，尤其是刀尖棱角位置，极易发生崩刃.

3）刀具前角改变对刀具受力的影响比后角改变更为显著，刀具前角增大，刀尖变得锋利，刀具切削受力减小，刀具后角增大，虽然刀尖也变得锋利，但切削力未有明显变化；刀具切削深度和速度越大，刀具受力越大；对于研究选用的直线形、圆弧形和折线形三种形状的刀具，切削力几乎相等.

4）在假定刀具不发生损耗的前提下，刀尖位置磨损情况最为严重，前角面次之，后角面最小，并且刀具前、后角越大，刀具磨损越严重，其中前角变化对磨损的影响大于后角，总磨损量与前角度数大致成正比，比例系数在（2.0～2.4）×10-9mm/［（°）·s］范围内；刀具磨损量也随着其切削深度、试件强度、切削速度的增大而增大，其中试件强度对磨损影响较大，而切削深度每增加一倍时，其刀具磨损量大致增加50%左右；刀尖棱角越多且棱角越尖锐，刀具磨损越严重.