散体介质复杂力链网络演化持续同调拓扑研究

王金安，杨 柳，李 飞✉

1) 北京科技大学土木与资源工程学院，北京 100083 2) 金属矿山高校开采与安全教育部重点实验室，北京 100083

散体介质是指由大量性质相似的、黏结性较弱或无粘结的固体颗粒组成的集合体，普遍存在于自然界中，尤其在矿山和岩土工程领域涉及甚广[1-2].例如，爆破后的矿岩、放顶煤开采顶煤、排土场砂土和滑坡堆积体等.因此，在矿山和岩土工程中，散体介质的力学行为和宏-细观作用机制的研究显得尤为重要[3-5].

散体介质的力学研究理论和技术方法有很多，诸多学者的研究表明：散体介质中由不均匀的链状结构（即力链）承担大部分荷载传递[6-8].这些力链之间相互交错，形成复杂、错乱的力链网络.如何定量化描述力链网络并发现合适的力链网络特征量是当前散体介质理论研究的重点[9-10].孙其诚等[1,11]从多尺度力学出发，以力链为桥梁，建立颗粒物质宏-细-微观多尺度结构，将力链网络视为半柔性网络，采用力链网络大小、力链长度、力链交点间距和力链半径等四个指标描述力链网络与土体力学性能的关联.杜克大学Behringer采用统计力学方法，对静态颗粒体系的局部力、矢量力、力的分布等特征参数进行了统计分析，取得了丰硕的成果[10,12-13].Vallejo等[14]采用箱形法确定了试样中力链的分形分布，证明力链强度的分形特性及其分布是导致颗粒材料在压缩过程中形成分形碎片的主要原因.以上研究主要聚焦于散体介质中的力链网络理论分析，对于将工程材料的力链网络特征量与演化过程相关联，特别是宏细观力学行为研究相对较少.

放顶煤开采是一种厚煤层开采工艺.开采过程中，顶煤经历了既有破坏—局部破坏—贯穿性破坏—破裂性破坏—运动性破坏五个阶段，在回采工作面附近，顶煤处于破碎运动状态，在宏观上表现出应变软化特征和散体流动规律[15-16].顶煤介质状态由连续向非连续和散体介质转换，内部应力场也呈现出由均匀向非均匀分布和离散接触力链网络分布形态发展.针对煤岩体非连续变形和复杂应力场特征，本文基于持续同调理论，从力学和几何的角度出发，建立了散体介质从接触网络到力链网络，再到拓扑空间模型的分析方法，定量分析放顶煤开采中力链网络的拓扑特征随工作面推进的变化规律，并探寻拓扑特征与矿压强度之间的关系.

1 持续同调理论

1.1 基本概念

持续同调（Persistent homology）是一种拓扑数据分析方法，它对点集进行多尺度分析，并识别其中的簇团、孔洞和空腔等拓扑结构，用于计算几何或者函数的拓扑空间特征[17-20].

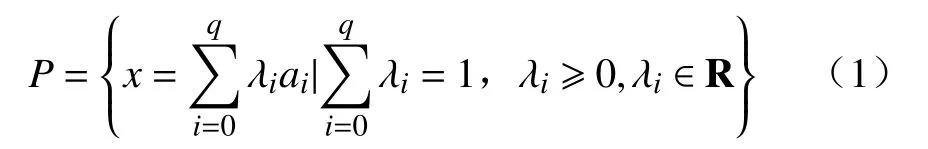
构成了q维单纯形，简称q维单形（q-dimensional simplex），记为 [s].其中序数组{λ0,λ1,…,λq}是q维单形的重心坐标.根据定义，当q=0时，0维单形即为一个点；当q=1时，1维单形构成一条线段；当q=2时，2维单形构成一个三角形面；当q=3时，3维单形即为一个四面体，如图1所示.更高维度的单形也存在，但对于平面网络分析，2维单形已经足够了.由的子集构成的单形称为[s]的面，例如对于2维单形，其任意一个边均为其1维面，任意一个顶点均为其0维面.

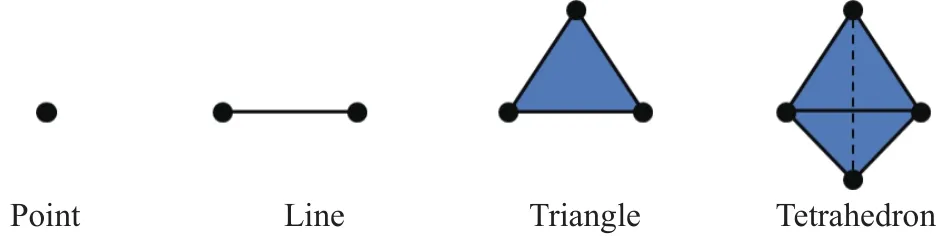
图1 不同维度的单纯形Fig.1 Simplexes in different dimensions

单纯复形K是有限个单形按照一定规则组成的集合，简称复形（Complex），以最高单纯形维度表示该复形的维度.复形满足以下条件：

（1）若 [s]∈K，则 [s]的任意一个面t∈K；

（2）K中任意两个单纯形的交集为空集或是它们的一个公共面.

如果在q-维欧式空间中存在一个点集P，由所有顶点距离不大于ε的单形构成的集合称为阈值ε的 Vietoris-Rips（VR）复形，即

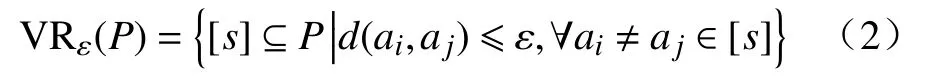
式中，d(ai,aj)表示顶点ai和aj的欧几里得空间距离，也是VR复形的权重函数，即

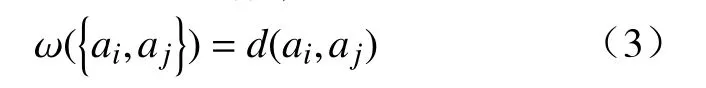
1.2 基于力链结构的 VR 复形

力链结构不仅需要包含散体介质的几何位置关系，还需要包含散体介质中颗粒的应力.因此，本文将（2）式VR复形的权重函数修改为如下所示：

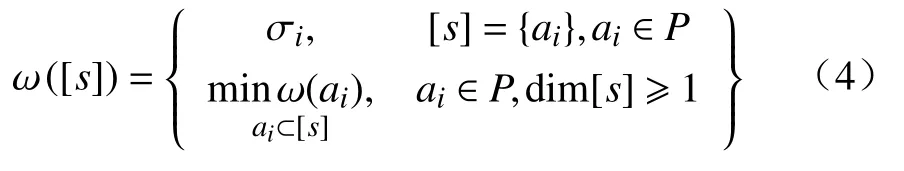
上式中 σi表示第i个颗粒内部的平均应力.

（4）式用该颗粒的平均应力表示为该点的权重，两个颗粒连线的权重用这两个颗粒平均应力的最小值表示，三个颗粒构成的三角形权重用这三个颗粒平均应力的最小值表示，以此类推.考虑力链网络中颗粒的接触关系，并以颗粒的平均应力作为阈值ε，重新定义的VR复形如下：

式中，ri和rj为相应颗粒的半径，dim[s]表示单形[s]的维度，阈值ε取值范围为[0, max(σi)].

根据公式（5），VR复形建立方法如下：

（1）剔除平均应力小于阈值ε的颗粒，剩余的每一个颗粒的圆心点即为一个0维单纯形，并将颗粒平均应力作为该0维单纯形的权重.

（2）判断 0 维单纯形中任意两个颗粒（a，b）的接触关系，如果接触，即(xa-xb)2+(ya-yb)2≤(ra+rb)2，连接这两个颗粒圆心点的边构成一个1维单纯形，并将两个颗粒平均应力的较小值作为该1维单纯形的权重.

（3）如果有三个1维单纯形首尾相连形成一个封闭的三角形，则该三角形即为一个2维单纯形，其权重为三个颗粒权重的最小值.

以上所有单纯形组合形成2维复形，这对于2维平面模型已经足够了.当然，如果是三维模型，即颗粒圆心位置为（xi，yi，zi），还需要继续向上建立3维复形.

图2（a）是一个由24个颗粒组成的颗粒体系，构成点集P1，在外部荷载作用下形成力链网络.图中顶点、边和三角形的颜色表示权重.σ¯为所有颗粒平均应力的均值，其中n表示颗粒数目，即：

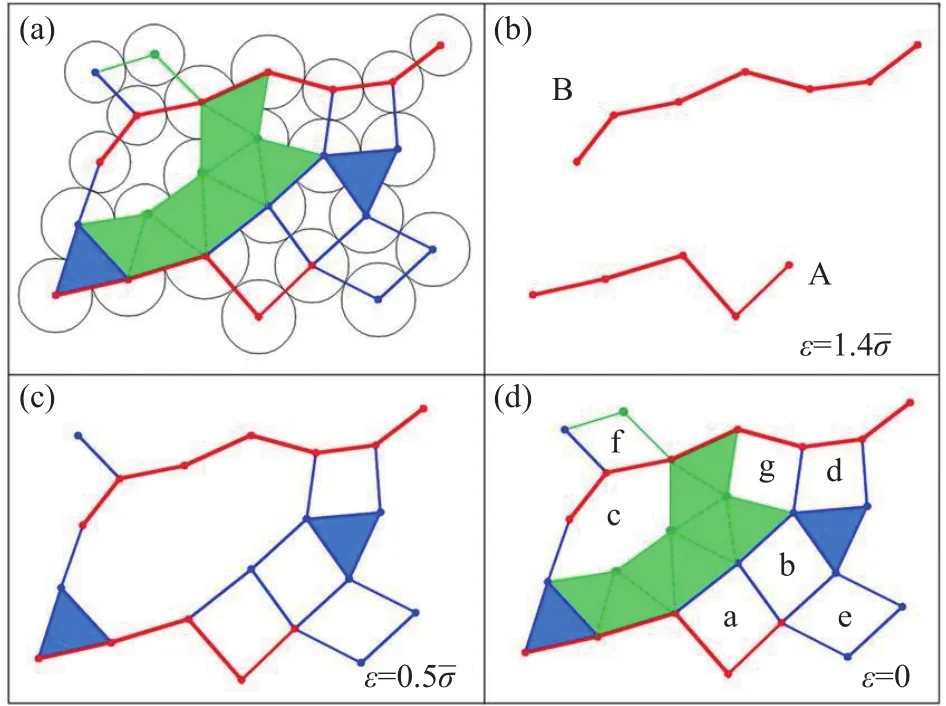
图2 力链网络.(a) 颗粒体系；（b）阈值为1.4倍平均应力时的力链网络；（c）阈值为0.5倍平均应力时的力链网络；（d）阈值为0时的力链网络Fig.2 Force chain network: (a) particle system; (b) force chain network with the threshold value of 1.4 times the average stress; (c) force chain network with the threshold value of 0.5 times the average stress; (d) force chain network with the threshold value of 0

当阈值 ε =1.4σ¯时，有12个0维单纯形和10个 1维单纯形，0个 2维单纯形（图2（b））；当阈值ε=0.5σ¯时，有20个0维单纯形，26个1维单纯形，2个 2维单纯形（图2（c））；当阈值 ε =0时，有 24个0维单纯形，40个1维单纯形，10个2维单纯形（图2（d）），图中连片的绿色区域表征其内部的力链网处于相同强度级别.显然有：

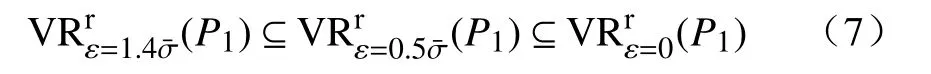
由此可见，在不同的应力阈值下，将呈现差异化的力链网络形态.当研究阈值持续变化时，所有的力链网络形态也将不断演进之中.这为建立颗粒集合体的宏观力学行为与细观力学演化机制关系提供了定量化的数学表征.

1.3 Betti数

拓扑数据分析中，用Betti数（βn）的概念表示复形的连通性.0维Betti数（β0）表示连通元素个数，1维Betti数（β1）表示闭合回路个数（组成回路的颗粒数量大于 3），2 维 Betti数（β2）表示三维空腔个数，以此类推.显然，在二维模型中，高维Betti数（n大于等于 2）均不存在.图2（b）～（d）复形的Betti数分别为：

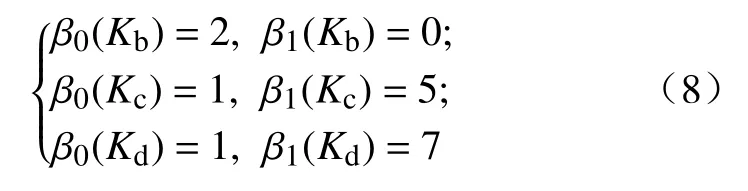
式中，Kb,Kc,Kd分别对应图2(b)、图2(c)和图2(d)中的单纯复形.

持续同调的优势在于，可以观测到当阈值ε连续地从颗粒最大平均应力（max（σi））→0时的一系列复形集合的连通数，并可观察到复形中的拓扑特性在何时生成（Birth），又在何时消失（Death）.

将图2（a）中的力链网络采用上述拓扑数据分析方法处理，可获得不同阈值ε下的拓扑特性（如图3所示）.从图3（a）中可以看出力链网络K中有两条生命周期较长的拓扑特征A和B，对应图2（b）中的两条红色强力链，并且这两条力链在ε=1.3时融合为一条.在大多数拓扑数据分析中，通常会认为出生点和死亡点相同或者生命周期较短的拓扑特征是噪点，但本文保留了出生点和死亡点相同的拓扑特征，并在图中以点的形式画出，因为这些拓扑特征也具有实际物理含义，并不能忽视它们.图3（a）中的每一个点表示在该阈值下有一个新的连通元素生成，但是在生成的一瞬间即被其他连通元素归并.图3（b）中有七条生命周期较长的拓扑特征（a～g），每个长条表示一个闭合回路，当然每个闭合回路的生命周期并不同.图3（b）中的每个点表示一个2维单纯形，这些单纯形在形成时也是一个闭合回路，但同时又立即被其他回路归并了.

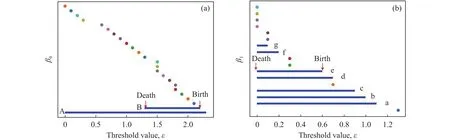
图3 持续同调条码图.(a) β0; (b) β1Fig.3 Persistent homology barcode: (a) β0; (b) β1

2 放顶煤开采光弹实验

以甘肃省某煤矿放顶煤工作面为例，该煤层埋深约400 m，煤层厚度约16.2 m，煤层倾角约平均6.6°.其上部基本顶为砂岩，厚度约7.9 m，岩性坚硬，呈厚层状结构.工作面采用倾斜分层走向长壁综采低位放顶煤采煤方法，全部垮落法管理顶板.根据现场对顶煤超声波波速测试[15]，工作面前方约12 m处顶煤发生超声波波速出现大幅跌落的现象，表明顶煤的宏观介质状态由连续介质状态向非连续介质和散体介质状态转化.在工作面支架上方至放煤口范围，顶煤由整体逐渐碎裂成块体，煤体基本丧失了黏聚力，呈现出散体特征，碎裂煤体通过接触摩擦承受和传递覆岩载荷，直至局部失稳产生运动性破坏.因此，本文将工作面前后方顶煤视为散体介质，采用光弹颗粒介质模拟放顶煤开采处于散体状态的顶煤介质，研究工作面附近散体顶煤的力链的形成机制和演化规律.

2.1 实验模型及方法

采用散体介质双轴加载双向流动光弹试验装置模拟工作面顶煤放出过程[6,21-24].根据工程地质条件和实验模型参数确定实验相似比.实验的几何相似比Cl=1∶79，容重相似比Cγ=1∶2.47，应力相似比Cσ=Cγ×Cl=1∶195.13，时间相似比Ct=Cl1/2=1∶8.88，满足欧拉准则Cσ×Ct2/(Cγ×Cl2)=1.

实验模型长度为1415 mm，相当于原型长度111.8 m，如图4所示.图中L1～L11表示模型左侧有11个颗粒释放口；B1～B26表示模型下部有26个颗粒释放口.为防止颗粒晶格化，实验使用直径分别为ϕ8 mm、ϕ10 mm和ϕ12 mm三种不同尺寸的圆形光弹颗粒，按照2∶9∶5的颗粒数量比例混合，模拟煤层和上部覆岩.考虑到基本顶比其他岩层较坚硬，抗拉强度更大，且随着煤层开挖发生周期性断裂，因此每3～5个弱粘结的方形颗粒密实排列，更能真实地模拟基本顶的弯曲、分离和周期性破坏等行为.

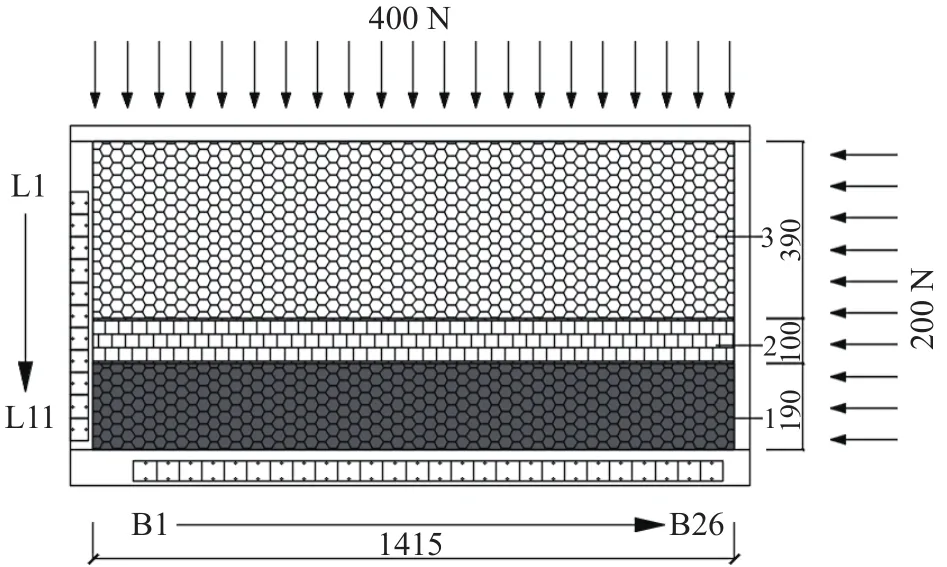
图4 光弹实验模型(单位：mm): 1—煤层; 2—基本顶; 3—上部覆岩Fig.4 Photoelastic experiment model (unit: mm): 1—coal seam;2—main roof; 3—overlying strata

在实验过程中，对水平和垂直载荷进行伺服控制.根据应力相似比，模型顶部施加荷载400 N荷载模拟上覆岩层荷载，侧向施加200 N荷载，模拟水平方向地应力作用.实验从B4放出口开始，B12放出口结束.每个开采步骤只有一个放出口打开，每次释放约100个颗粒.经统计[23]，试验框内单位面积内的颗粒数为1.154 cm-2，根据几何相似比，100个颗粒换算成实际开采面积为54.1 m2.释放口宽度为5 cm，每一次开采相当于在实际开采长度3.95 m范围内，放出54.1 m2的顶煤.

实验中，每放出一次颗粒拍摄一组光弹照片，并对光弹图片进行图像处理，获取颗粒的位置、半径和平均应力[23-24].

2.2 力链演化

通过光弹实验，用相机拍摄到不同工作面推进距离时的光弹图像（图（5））.从图中可以直观的看出力链强弱及力链演化过程.

初始状态下（图5（a）），围岩应力未受到煤层开挖的影响，采场中的力链交错分布，排布均匀.基本顶内部应力较强且连续.上覆岩层与基本顶交接处并非笔直的链状结构，而是诸多倒“Y”型力链，与基本顶形成一个三角形的稳定结构，将上部荷载传递至基本顶中.类似的，基本顶中的荷载向煤层中传递时，力链结构呈“Y”型.

在B6口释放了99个颗粒后（图5（b），图中绿色圆点之间区域表示放出口，下同），基本顶发生轻微弯曲，内部力链不再连续.采场周围由于顶煤的释放，内部应力减小，力链强度减弱甚至消失.工作面前方煤岩和重新压实的采空区中形成力链集束，力链集束的底部向外侧倾斜.此时顶煤释放形成的力链集束尚未贯穿基本顶，但是基本顶上方的力链结构形态已经发生变化，原先的环状力链结构扩张，形成更大的环状力链结构，内部包含的未受力颗粒数量更多，表明煤层开采后，上部覆岩中有更多散体岩块处于低应力或无应力状态，不承担支撑和传递荷载的作用.

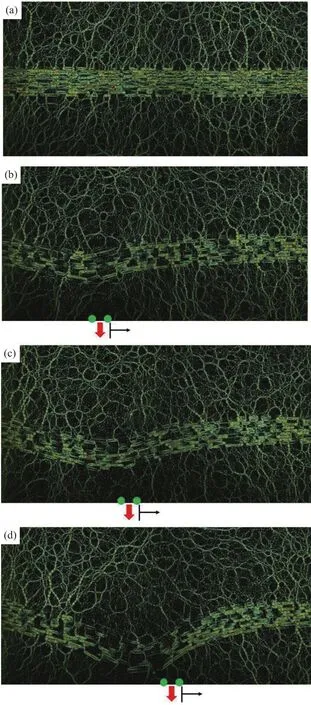
图5 放顶煤开采光弹力链网络.（a）工况 0（初始状态）；（b）工况 3；（c）工况 5；（d）工况 8Fig.5 Photoelastic images of force chains in top coal caving mining:(a) initial state; (b) mining step 3; (c) mining step 5; (d) mining step 8

随着工作面的推进，在B8口释放了105个颗粒后（图5（c）），基本顶进一步弯曲，工作面围岩力链发生偏转，工作面前方煤岩和采空区中的力链集束向上延伸，穿透基本顶，并在基本顶上方闭合，同时覆岩中部分环状力链破断，形成完整的拱形应力壳结构.应力壳外侧应力较强，而内侧应力较弱.该拱形应力壳的前拱脚位于工作面前方，后拱脚位于重新压实的采空区.

当 B11口释放了 108个颗粒后（图5（d）），基本顶彻底破裂，破断面无水平传递的力链.应力壳结构随着工作面的推进而迁移，采空区中冒落的矸石经过充分压实，力链强度逐渐恢复.

采用G2法[25]，计算光弹照片中颗粒内部平均应力，继而计算出整体的力链平均强度，如图6所示.图中，工作面前方是指图5中以箭头处为起点，沿工作面推进方向位于基本顶下方未开采顶煤；顶部覆岩是指相同区域基本顶上部覆岩.当煤层初次开采后，顶部覆岩和工作面前方煤岩中的力链强度迅速下降，根据长度相似比，在工作面实际掘进11.85 m处出现初次来压现象，之后又出现了两次老顶周期来压，来压步距分别为7.9 m和11.85 m，模拟结果略小于现场监测结果.动压系数分别为1.27和1.50.整个过程中顶部覆岩和工作面前方煤岩力链强度增减趋势一致.

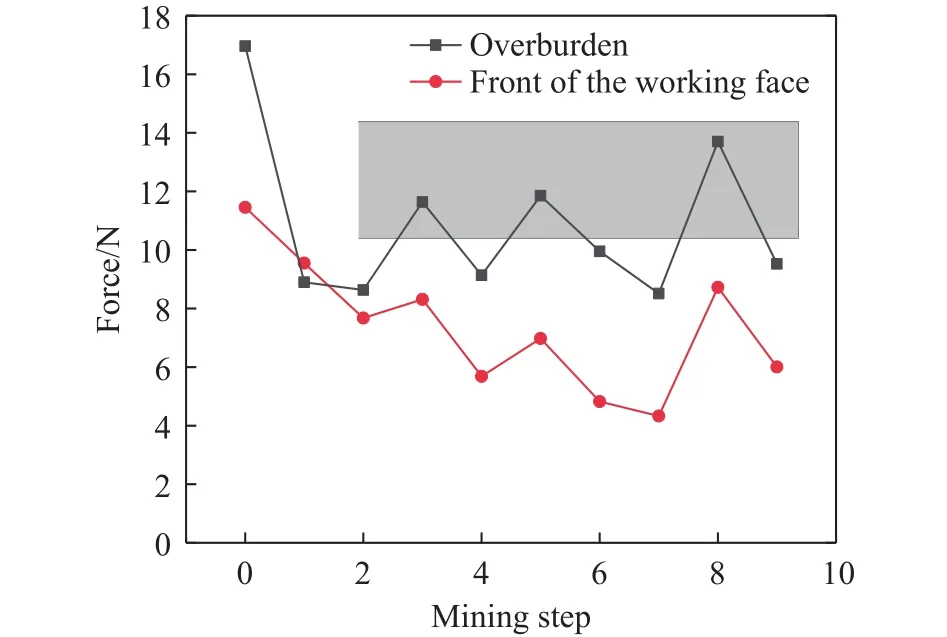
图6 不同工况下的力链平均强度Fig.6 Average strength of force chains under different mining steps

试验表明：放顶煤开采过程中，由于顶煤的释放，工作面附近的力链强度始终处于较低水平，力链网络发育不明显，大部分散体岩块处于低应力状态，不承担支撑上部荷载的作用.在基本顶弯曲带和工作面前后方产生力链束集中区，并向上延伸在基本顶弯曲带上方闭合，宏观上形成拱形力链结构.力链拱内外力链强度和力链网络截然不同，力链拱内应力强度普遍低于平均强度，且强力链拱脚位置随着工作面的推进而变化，基本上位于工作面前后方支承压力峰值区.光弹实验测量到的力链强度周而复始的波动现象，与实际放顶煤开采过程中老顶的周期来压过程基本吻合.

3 放顶煤开采力链网络持续同调分析

同调是一个静态的概念，而持续同调是连续、动态的过程.为了进一步分析放顶煤开采中的力链网络在开采过程中的演化过程，分别对工作面（即放出口）上方的覆岩区域和工作面前方区域进行力链提取，截取的区域高和宽均为三倍放出口宽度.对提取后的力链网络用第一节中的TDA方法进行持续同调分析.为了方便数据处理，定义：

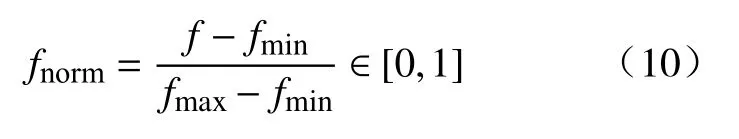
式中，fmin和fmax分别表示f的最小值和最大值.因此阈值ε取值范围为[0,1].

将f=1带入（10）得fnorm≈0.3，即力链网络平均强度归一化后约等于0.3.将力链强度划分为以下三个等级：

3.1 顶部覆岩力链分析

图7为顶部覆岩初始状态下的β0条码图.条码图中的表示的拓扑特征可以分为两类，第一类用蓝色的条码表示，每一根条码代表一个力链连通体，条码两端对应的x轴代表该连通体的生成阈值和死亡阈值.第二类用彩色点表示，它表示在该阈值下有一条力链生成，但又立即归并到其他力链结构中.大部分连通体的拓扑特征结构属于第一类.

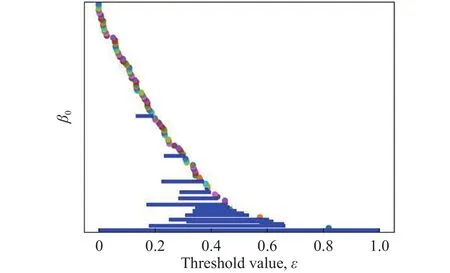
图7 顶部覆岩初始状态下的β0条码图Fig.7 β0 barcode of the initial state in the overburden

从图7中可以看出在阈值ε=1时，第一条力链连通体出现，并且在ε→0的过程中，不断有连通体出现，这些连通体有些作为独立力链存在一段时间，有些立即消失，但最终都归并入第一条力链连通体，即当ε=0时，密实颗粒体系中的所有颗粒通过接触关系相互连接，形成一个连通的整体，如图8所示.

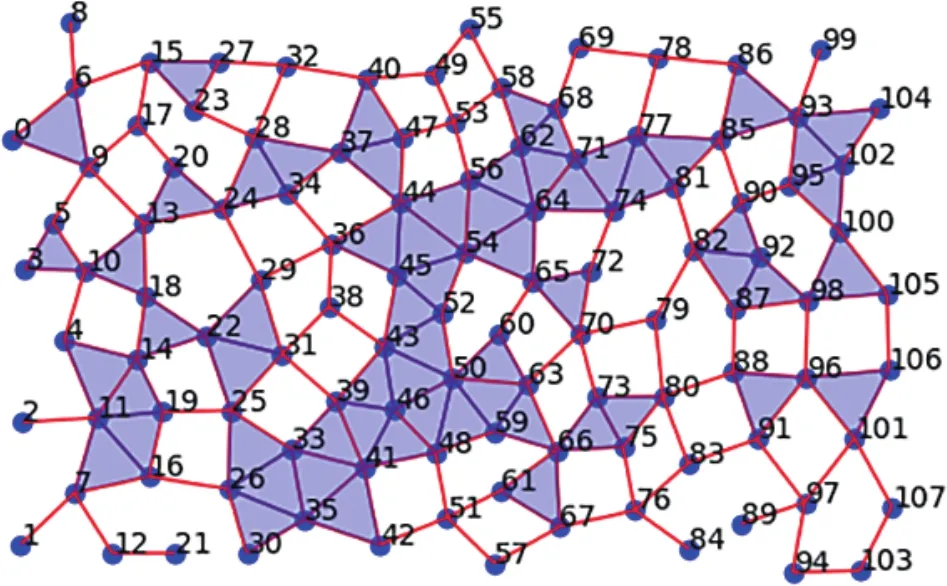
图8 接触网络（初始状态，ε=0）Fig.8 Contact network (initial state, ε = 0)

对于β1条码图（图9），条码图中的表示的拓扑特征也可以分为两类：第一类用蓝色条码表示，它代表一个力链闭合回路（组成回路的颗粒数大于等于4），条码两端对应的x轴代表该连通体的生成阈值和死亡阈值.第二类用彩色点表示，它表示一个3颗粒稳定闭合回路的生成，同时由于它形成了2维单形，它作为一个整体被并入其他回路中.大部分环状力链的拓扑特征属于第一类.由于大于等于4个颗粒组成的回路不稳定，因此由四个及四个以上的颗粒组成的闭合回路称为“缺陷”回路.

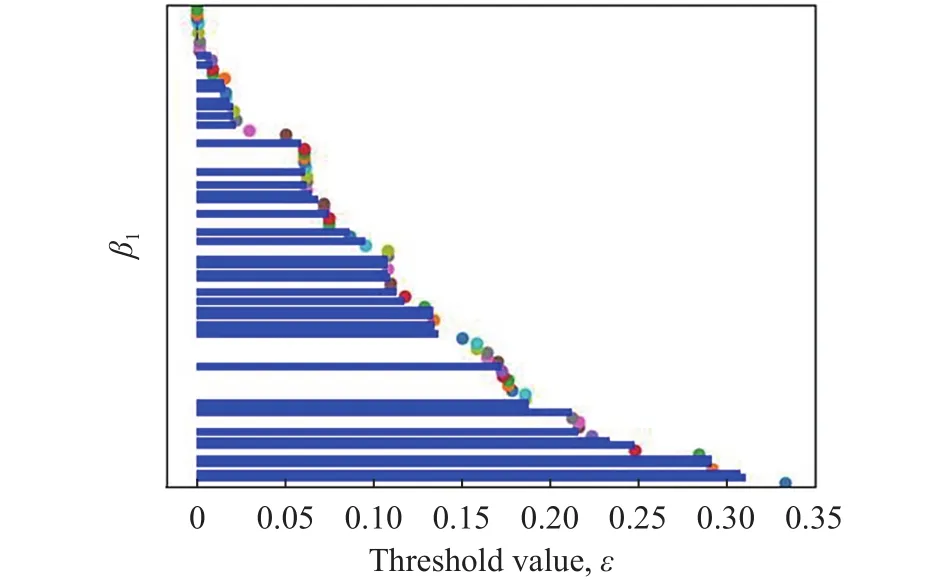
图9 上部覆岩初始状态下的β1条码图Fig.9 β1 barcode of the initial state in the overburden

根据条码图，获得顶部覆岩不同工况下Betti值随阈值变化曲线（图10（a））.曲线整体呈抛物形，其中工况3,5,8的β0的峰值在ε∈[0.3, 0.4]左右，属于强力链范围.且工况3,5,8的峰值均不小于初始状态下的峰值，尤其是初次来压时（工况3），峰值远远高于其他工况.说明在老顶来压时，顶部覆岩强力链多且分布较为离散.工况2,4,7的β0的峰值低于初始状态，且峰值来的更早些，ε∈[0.2, 0.3]，属于次强力链范围.工作面来压前，顶部覆岩主要是次强力链，且分布集中.煤层开采造成老顶一定程度上的回转，从而导致顶部覆岩的力链重新分布，原先的次强力链演化为强力链.

曲线整体呈 L 形分布（图10（b））.β1在 [0, 0.2]区间内与ε近似呈反比，在[0.3, 1]区间内趋于0，顶部覆岩中强力链网络几乎不存在环状力链，即“缺陷”回路.说明顶部覆岩中的强力链网络无论是强度上还是构型上都较为稳定.将ε∈[0, 0.2]区间的数据进行线性拟合，β1～kε，k是比例系数，衡量β1随ε变化的快慢程度.不同工况下的k值如图10（b）中所示，可以看出来压时的k值更小，意味着β1随着阈值ε增加而下降的更快，当k小于-220时的工况3、5、8均为周期来压时的工况.同时当ε=0时，来压时的β1更大.这是由于老顶来压虽然使顶煤覆岩内部形成更多强力链，但这些强力链和次强力链，弱力链形成结构上更为脆弱的“缺陷”回路，因而在结构上更不稳定.

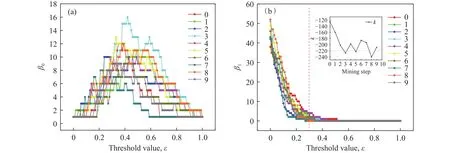
图10 顶部覆岩不同工况下的Betti数随阈值ε变化曲线.(a) β0; (b) β1Fig.10 Curves of Betti values vs ε under different mining steps in overburden: (a) β0; (b) β1

3.2 工作面前方煤岩力链分析

工作面前方煤岩Betti数随阈值变化曲线如图11所示.来压时的β0的峰值位于ε∈[0.2, 0.3]区间内，属于次强力链范围.说明工作面前方煤岩的力链强度低于顶部覆岩，结果与图6一致.工况2,4,7的β0的峰值位于ε∈[0.3, 0.4]区间内，这一现象恰好与顶部覆岩相反.但其峰值依然低于初始状态峰值.来压前，工作面前方煤岩力链发育稀少但相互之间连通性较好，来压后产生较多次强力链，从侧向支撑强力链的发展，但力链之间连通性较差.

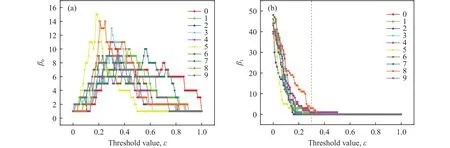
图11 工作面前方煤岩不同工况下的Betti数随阈值ε变化曲线.(a) β0; (b) β1Fig.11 Curves of Betti values vs ε under different mining steps in front of working face: (a) β0; (b) β1.

工作面前方煤岩力链网络的β1在[0, 0.2]区间内与ε近似呈反比，在[0.3, 1]区间内趋于0，与顶部覆岩规律相同.但来压时，3、5和8工况并无统一特征.

4 结论

针对散体介质复杂力链网络数学描述和定量分析难题，持续同调拓扑分析力能克服传统连续介质模型的力学假设，更真实的反映散体内部力的传递机制.本文以放顶煤开采为背景，建立了从接触网络到力链网络，再到拓扑空间数学模型的理论，提供了一种新的散体介质力链网络分析方法，构建起散体介质细观力学机制与宏观力学行为的桥梁.

（1）散体介质中的大量颗粒可以抽象成一个数据库，持续同调的意义便是在于能持续性的观测数据随着阈值连续变化时的特征变化，观察到数据的同源特征，避免了忽略或者消除大数据中的细小特征.将散体颗粒应力作为阈值，可观察力链网络在不同强度阈值下的力链演化过程.

（3）Betti数可以作为一种预测来压的力链网络参数.顶部覆岩和工作面前方煤岩力链网络β0曲线呈抛物线形，且来压时抛物线峰值高于初始状态下的峰值.不同之处在于顶部覆岩β0峰值位于强力链范围，而工作面前方煤岩β0峰值位于次强力链范围.

（3）放顶煤开采过程中，顶煤覆岩β1曲线近似呈L形，在[0, 0.2]区间内与ε近似呈反比，在[0.3,1]区间内趋于0.通过对比顶部覆岩β1与阈值ε在[0, 0.2]区间内的反比系数k，得出来压时β1随着阈值ε增加而下降的更快，结合ε=0时的β1值，表明来压时，顶部覆岩虽然产生较多强力链，但这些强力链与次强力链、弱力链相结合，形成“缺陷”闭合回路，因而在结构上更不稳定.

（4）持续同调理论提供一种全新的散体介质力链网络分析思路，该理论用于放顶煤开采覆岩与顶煤力链演化研究中，从力链角度揭示了放顶煤开采过程中的矿压演变规律.

持续同调拓扑方法可以推广至研究其他散体介质中.将持续同调拓扑特征与散体介质细-宏观力学行为相结合，将深刻揭示力链网络结构的变化和散体介质力学响应之间的关联机制.