多相混合渗流理论研究

朱维耀

1) 北京科技大学土木与资源工程学院，北京 100083 2) 北京科技大学应用力学研究所，北京 100083

多相流体在多孔介质中的流动是一个复杂的力学、物理过程，多相流体混合渗流伴随着质量、动量、能量、热的变化，当有相间掺混作用特别是化学剂存在下相混合掺混现象更为明显.对于反映该过程的讨论特别是动力学本质的研究还不多见，人们只是把研究单相渗流的经典方法，将各相均作为独立的相推演到多相渗流中.1936年Wyckoff和Botset以相对渗透率来描述两相流体渗流[1]，但没有考虑两种流体之间的相互（耦合）作用，且认为流体-流体界面和流体-固体界面处的边界条件是相同的，事实上这并不正确.许多学者通过体积平均（Volume averaging）法[2]来获得耦合渗流控制方程，这种模型根据达西定律直接推广而来.对于两种互不相溶的流体耦合渗流过程，1988年以来Walter Rose对单相流推广到多相流的渗流关系进行了修正，突出了两相间的相互作用关系，给出了广义的达西关系式[3-5]，方程中有四个待定系数来表征两相间相互作用[6]，其中相对渗透率是饱和度的函数.许多研究通过渗透率和毛细压力之于饱和度的关系改进模型[7-8]，或者建立渗透率与毛管数[9]、黏度比[10-11]和润湿性[12]之间的联系.一些研究从流体界面的拖曳现象和动量交换出发，提出了附加耦合项[13-15]，说明了渗透率对相分布的作用.热力学过程也被用于构建多相流模型[16-19]，尽管一些参数的定义略有差别[20]，其与体积平均法具有类似的形式，系数中有两个非对角项表征界面黏性耦合[21]，黏性耦合也逐渐应用到渗吸流的研究中[22-24].对于多相流动问题，仍多使用经典多相流理论来解决[25-27].对于相对渗透率实验曲线端点附近出现了其他相为非连续相流动问题，均还未见对其掺混机制及相对渗透率多参数函数关系的考虑.

为此，鉴于目前的研究局限，我们从反向思维的角度出发来分析多相流体在多孔介质中的流动状态，突破原有多相渗流理论基于流体力学各相均为连续相假设的局限，把多相流体作为一个整体考虑，引入多相体系渗流平衡热力学定律，基于总的守恒方程，研究多相流体在多孔介质中传输，含不相溶、相界面变化、质量传输的混合流体，搞清混合流体在多孔介质中的各相间转换作用关系和流动机制，建立多相混合渗流理论和模型，揭示多相流体在多孔介质中的混合流动规律，期待解决渗流中多相混合渗流问题并发展渗流力学的新理论.

1 渗流过程中多相体系平衡热力学

多相流体混合渗流存在质量、动量、能量、热的变化等.用传统的方法处理渗流的物理化学规律和机理显然不能得到正确的认识.要想更好地研究多相流体的传输变化规律，必须考虑力学、物理、化学复合过程的热力学行为.为此，我们将从多相流体在多孔介质中混合渗流过程的热力学入手，阐明渗流平衡热力学规律，提出对渗流的热力学新认识.

1.1 渗流热力学第一定律

考虑为稳流过程，多相流体渗流传输发生能量交换，还存在着物质交换.因此，这种物系为敞开物系.该物系的热力学规律为：

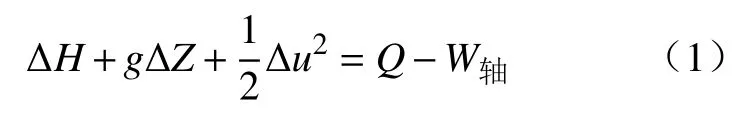
其中

式中：H为焓；U为内能；P为总压力；V为体积；g为重力；Z为高度；u为截面平均流动速度；Q为热；W轴为轴功.其中，当W轴为正即物系对环境做功，W轴为负即环境对物系做功.

由式（1）可知，渗流热力学第一定律公式型式有别于封闭物系的第一热力学定律的型式.由此阐明了渗流过程的热力学推演规律.

1.2 渗流热力学第二定律

根据热力学原理，对于孤立体系，体系、环境为可逆过程，则体系为孤立体系，有

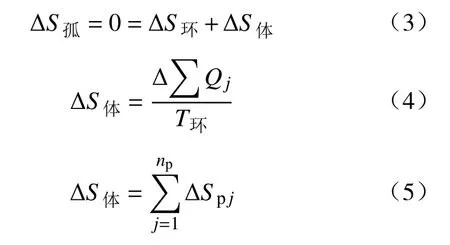
式中：S孤为孤立体系的熵；S环为环境的熵；Qj为j相的热；；np为相的数量；Spj为j相的熵；T环为系统环境的绝对温度.

可得：

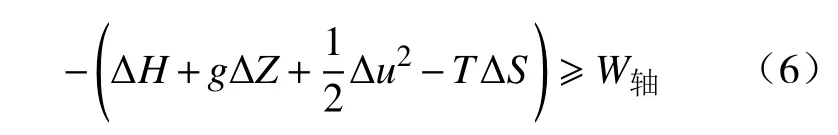
因为，G=H-TS，式（6）又可改写为：

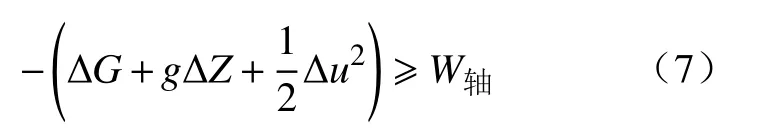
式中，G为自由能（Gibbs）.式（6）或（7）即为渗流热力学第二定律公式型式.

1.3 渗流过程中的多相体系平衡条件和热力学关系

多相体系的平衡条件是：①热平衡条件；②力学平衡条件；③相平衡条件；④化学平衡条件.如果各相间热平衡，则温度Tj=Tj′（j≠j′），j′=1,2,3,…,np；力学平衡，压力Pj=Pj′；相平衡，化学势 µj= µj′；化学平衡条件为：各物性参数不随时间而改变fi(t)=const （fi(t)为时间函数关系）.

对于渗流过程，如果T体系=T环境，则平衡时：

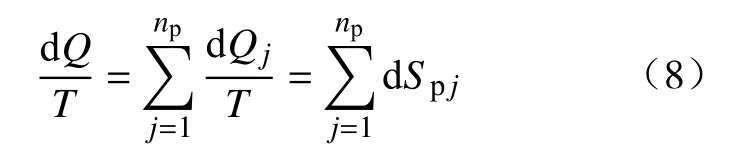
力学平衡相间压力为：

式中，Pc为毛管力.

相平衡化学势为：

式中，j代表相为相数量，i代表组分 (i=1,2,3,···,nk)，nk为组分数量.

对于各相写为

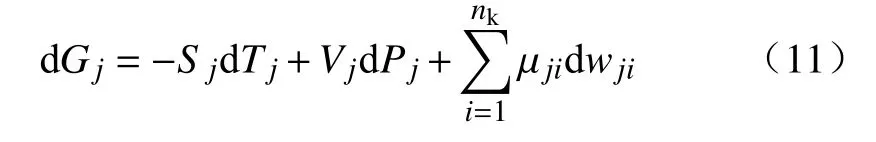
式中，w为物质的量.且流体自由能（Go）为

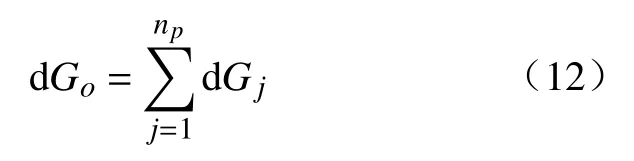
对于多相渗流流体体系，视自由能Ga为

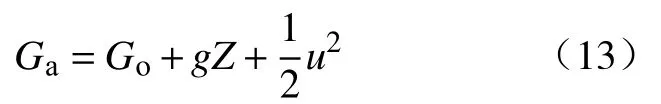
对于渗流过程ua

式 中：ua为 渗流 流体 的 流速 ； ϕeff为 多 孔介 质孔 隙度.则式（13）进一步写为

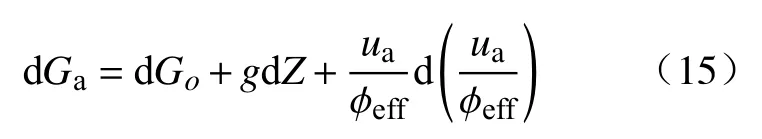
由此可见，多孔介质的非均质和渗流速度的变化将引起视自由能（Ga）的变化.

2 多相流体混合渗流理论模型

2.1 质量守恒规律

多相流体混合渗流时，各相的饱和度是变化的，流体的不断重新组合、分配，如有相态变化发相间质量传输，如有化学剂融合反应发生相间质量传输，多相混合反映为渗流过程的复杂性，但是作为总的客观体其守恒规律是不变的.因而，总的质量守恒方程为：

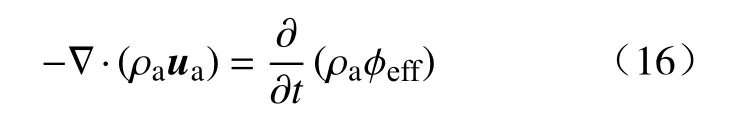
式中： ρa为流体的混合密度；ua为ua的向量式；t为时间.

流体的混合密度(ρa)定义为：

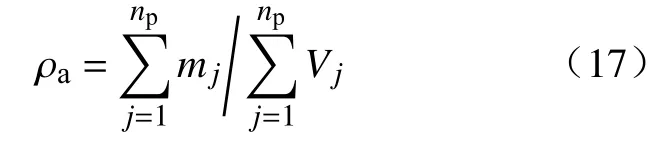
由ρj=mj/Vj， 得：

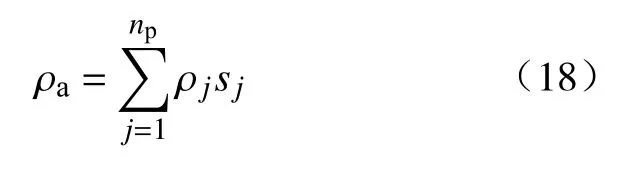
式中：m为相的质量；s为相饱和度.

式（16）即为多相混合渗流的质量守恒规律.

2.2 混合渗流运动规律

首先，我们根据前面的结果，假设混合渗流速度与总压力梯度成正比关系的存在是可能，来分析混合渗流机制，揭示多相渗流规律.由式（7）知道，对可逆过程：

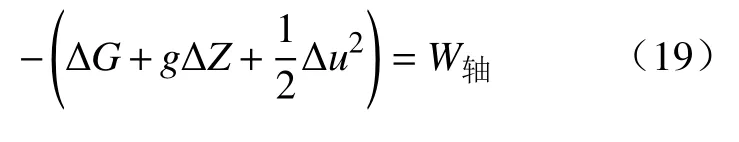
因为流体渗流时，产生界面.因此，自由能分为两部分，一部分是体相自由能，另一部分是界面自由能.写为：

式中：Gb为 体相自由能；Gf为界面自由能.

自由能又可表示为各相之和，即

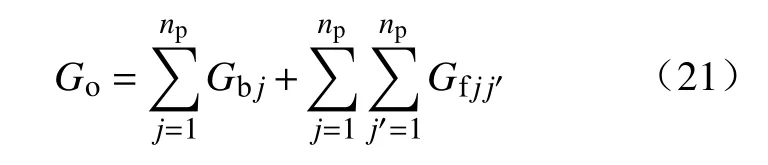
界面自由能可以表示界面张力与界面积之积：

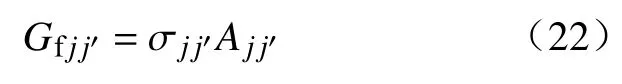
式中：Ajj′为相间界面积，j=j′时为j相与固相的界面积； σjj′为j相与j′相间的界面张力.因而

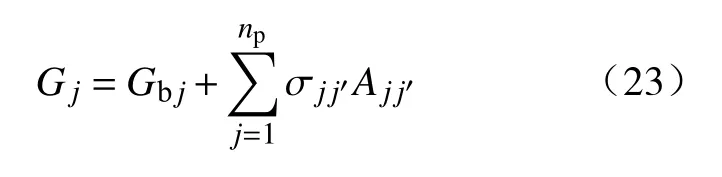
因此流体自由能Go表示为：

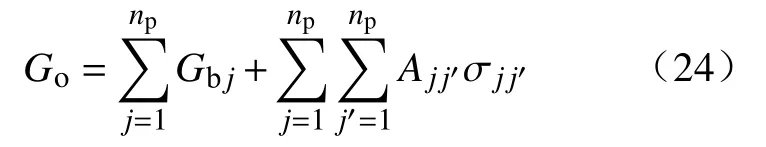
将式（24）代入式（19）得：

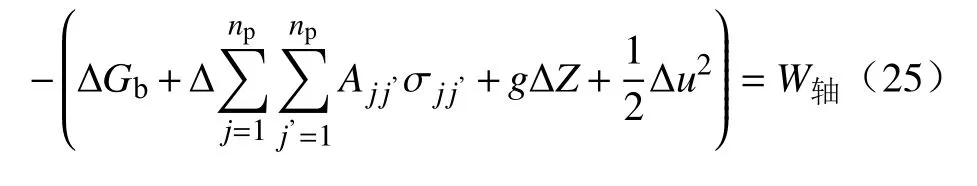
因为界面上流体所占体积很少，忽略其对体积变化的影响，所以有：

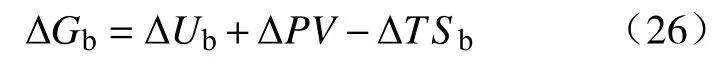
式中：Ub为体相内能；Sb为体相熵.

于是式（25）变为

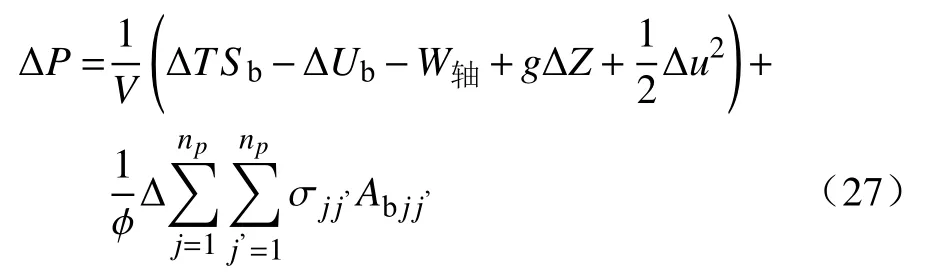
其中

式中：Abjj′为单位岩石和流体体积中的相界面积大小；ϕ为孔隙度；Vtotal为介质和流体体积之和.

因此，由式（27）可以看出，渗流流体混合渗流时，由于内能、热能、动能、势能、界面能和做功的变化引起压力差的变化.

如果体系无热量、内能、势能和动能的变化，且环境对体系无做功，则

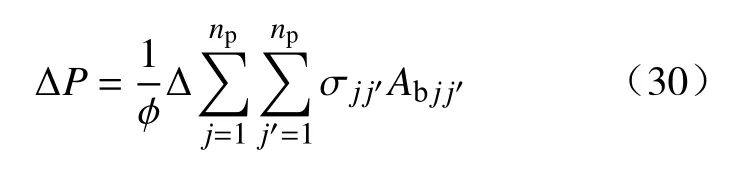
此时界面大小发生变化，必引起压力大小的变化.

对于无相变，无化学反应，无热交换的多相混合体系，其渗流的机制是属力学、物理的范畴，其作用结果如式（30）所示.由式可以看出，若使多相流体混合程度增大，必须加大压差，产生相界面，反映为相饱和度的接近，渗流阻力增大，各相渗透率之和降低.若使流体从定流量流出，压力差的一部分必须用于产生界面的消耗，写为

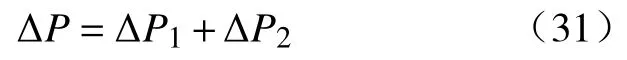
式中， ΔP1为流体流动消耗的压差； ΔP2为产生界面消耗的压差.

依据渗流实验和理论所知：

式中，M为流动度，L为流道长度.

那么对于多相混合渗流流体，ua～ΔP1，有：

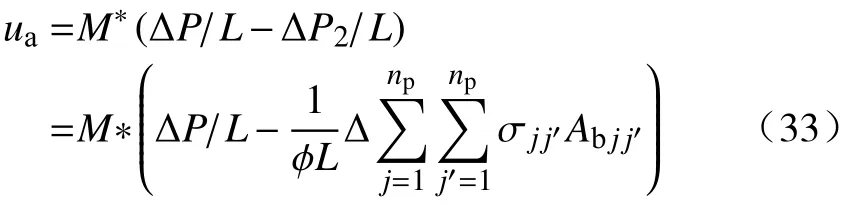
式中，M*为基准流度.式（33）又可写成下列形式：

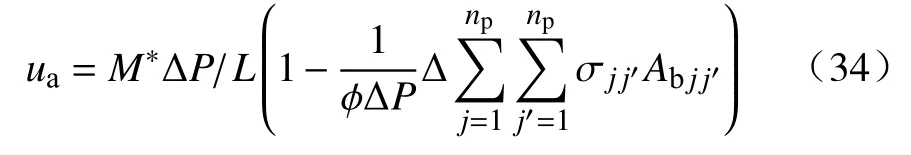
即

令

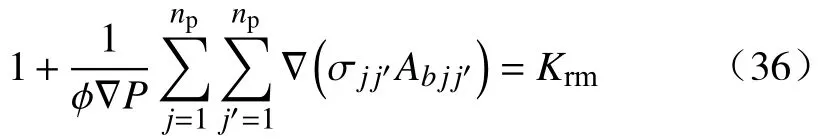
式中，Krm混合渗流系数.则式（35）变为：

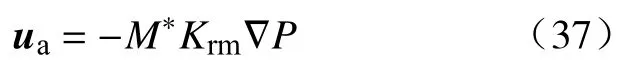
由此可见，Krm是界面、界面张力、压力梯度和孔隙度的函数.

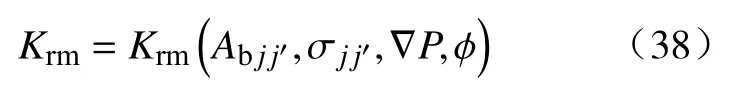
令

式（37）又为：

这里我们称Mm为混合渗流流动度，其与Krm是反映多相流体性质、多相混合渗流性质、孔隙介质物性的函数.式（34）又可写成下列形式：

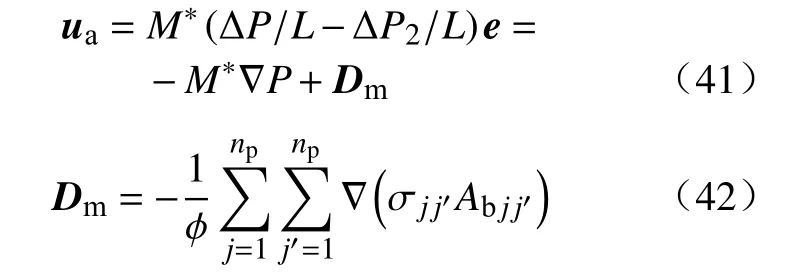
式中，e为基矢量.由此混合渗流运动规律得出，即式（37）或式（40）的结果.

3 多 相混合 渗流理 论与传 统多相 渗流理论的关系

由上面研究可知，多相混合渗流理论揭示了多相流体混合渗流的规律，阐明了渗流的总体效果，而多相渗流理论把达西定律推广到了多相渗流中，它的局限性在于仅假设为连续相，忽略了相间的交换，相对渗透率仅视为是饱和度的函数，计算相渗透率时又忽略了毛管力.但实际的相流动在一定情况下是非连续的，相间存在交换，而实验时所测得的压力是总体压力，测量结果在理论上和应用上有一定的差异，可见多相渗流理论存在局限和不足.下面进行等价分析，确定多相混合渗流理论与传统多相渗流理论的关系的内在联系.

由多相渗流理论可知，多相渗流总的速度是：

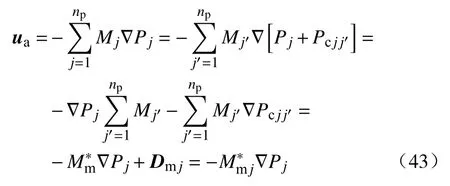
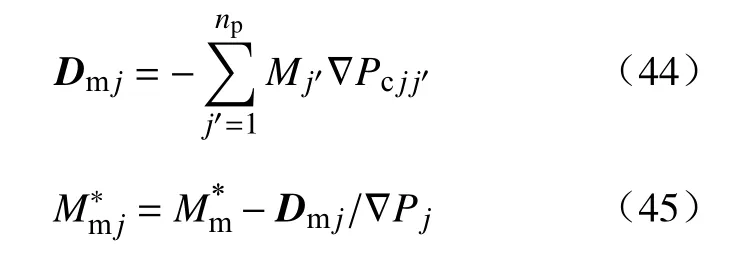
由此可以看出式（43）与多相混合渗流运动方程式（40）类似.这种结果并非偶然，式（43）中是饱和度、毛管力、相压力梯度的函数.而式（40）中Mm混合渗流程度是界面、界面张力、压力梯度的函数.根据已知的关系，如渗流的物理、力学特性及饱和度、毛管力的关系：

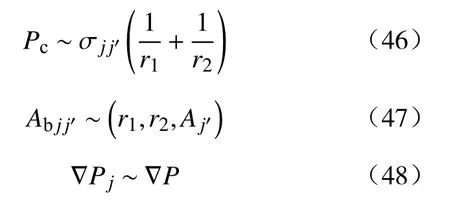
式中，r1和r2为界面的两个主曲率半径.

如果式（46）和（47）关系已知，就可以确定混合渗流理论与多相渗流理论的一切参数关系，从而对多相渗流理论进行修正.两个理论的不同和差异性对比见表1.

表1 两种理论的差异性对比Table 1 Contrast between the two theories

4 多相混合渗流理论的应用

根据上面的研究结果，多相流体混合渗流时质量守恒方程应遵循式（16），运动方程应遵循式（37）或（40）的形式，即-Mm∇P，ua=-M*∇P+Dm.

如果相界面梯度不发生变化，则

此种情况最明显的例子是单相流动的情形，基准流度的意义由单相流给出.

式中，K*为绝对渗透率； µ*为基准相黏度.

下面我们来考虑压力方程.如果将式（37）代入式（16）中，有

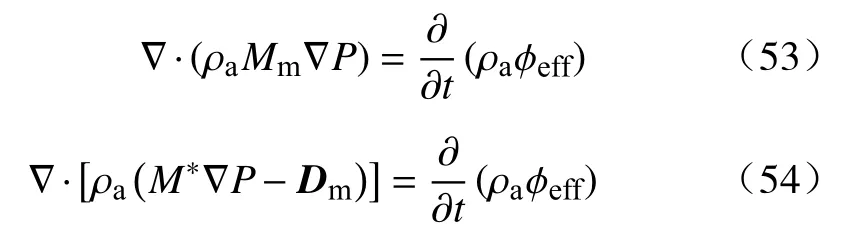
式（53）或（54）即为混合渗流的压力特征方程，如果Mm和Dm已知，即可求其解.该方程比多相渗流的压力方程求解方便得多.在多相渗流计算时，因为无法指明总压力P与j相压力Pj的关系，所以一般处理为忽略毛管力，让相压力等于总压力（Pj=Pj′=P）.因此，可以看出多相渗流理论的不足和混合渗流理论的优越性.混合渗流理论有着深刻的物理含义，与实验现象、规律相符，具有广阔的应用前景.

5 实例分析

例如水、油两相一维渗流体系：

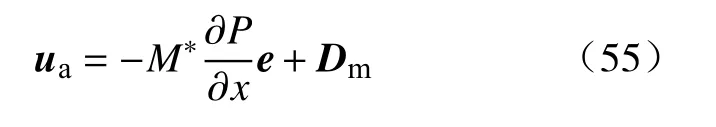
式中，x为维度坐标.

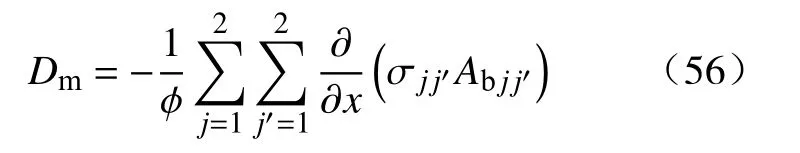
式中，Dm为Dm的标量式.当油水润湿性为中性，接触角为 90°，所以式（56）可写为：

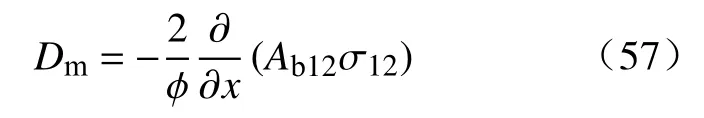
一般 σ12为常数，又令：

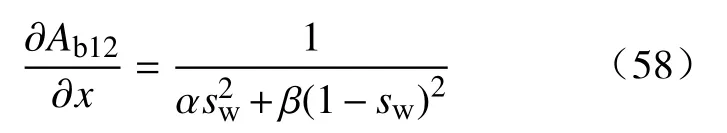
式中：sw为水饱和度；α和 β为常系数.

则

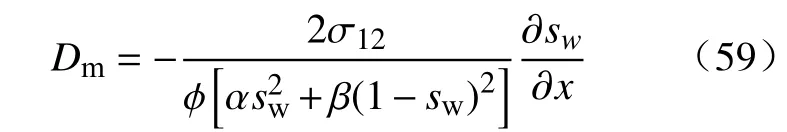
取 α =1， β =1，有：

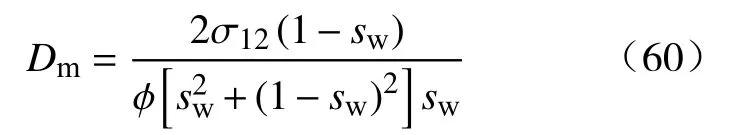
所以运动方程写为

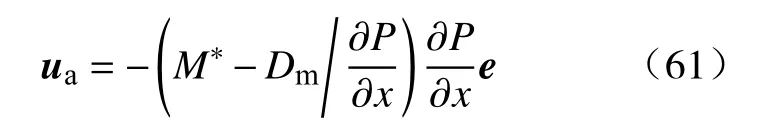
如果不考虑压力梯度对混合渗流速度的影响，

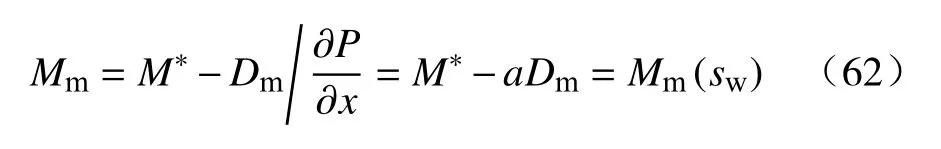
式中，a为常系数.由此退化结果与多相渗流理论公式完全一致，这时多相渗透率之和仅是饱和度的函数，即相对渗透率仅是饱和度的函数.由此可以看出：这种情况仅是多相混合渗流理论中混合渗流程度的最简化形式，多相混合渗流理论包含了多相渗流理论的内容.

6 结论

(1) 多相体系流体总的渗流速度与压力梯度成正比，与多相体系混合渗流程度有密切关系，混合渗流程度是饱和度、界面张力、压力梯度的函数.多相流体混合渗流运动方程式是：ua=-Mm∇P，

混合渗流程度Mm是反映多相流体性质、混合渗流性质、孔隙介质物性的函数.混合渗流系数Krm是界面、界面张力、压力梯度和孔隙度的函数.

(2) 通过多相体系平衡热力学条件下热力学第一、第二定律的推演，给出了渗流热力学第二定律公式型式.分析指出了多孔介质的非均质和渗流速度的变化将引起视自由能（Ga）的变化，且多相流体混合渗流过程中，由于内能、热能、动能、势能、界面能和做功的变化引起压力差的变化.若使多相流体混合程度增大，必须加大压差，产生相界面，反映为相饱和度的接近，渗流阻力增大，各相渗透率之和降低.

(3) 多相混合渗流理论弥补了传统多相渗流达西理论的不足，揭示了多相流体混合渗流的规律，阐明了渗流的总体效果，而多相渗流理论把达西定律推广到了多相渗流中，它的局限性在于把各相假设为连续相，但实际在一定情况下分相流动是非连续的，实验时所测得的压力是总体压力，用推广的达西定律计算相渗透率有时又忽略了毛管力.因此，相对渗透率的测量结果在理论上和应用上存在一定的差异.根据混合渗流理论与多相渗流理论的参数关系，可以对多相渗流理论进行修正.

（4）理论分析结果表明，多相混合渗流理论模型退化结果与多相渗流理论公式完全一致，此时混合渗流系数与相对渗透率完全相同并仅是饱和度的函数.当包含不相溶、相界面变化、相间传质传输、混合相、非连续相时，混合渗流程度是饱和度、界面张力、压力梯度和孔隙度的函数.说明现有的多相渗流理论其相对渗透率仅是饱和度的函数，是非常理想的流动情况.多相混合渗流理论包含了多相渗流理论的内容.

致 谢

马启鹏、卜文港同学参加了本文的文字图表和公式编排工作，在此表示感谢.