基于分布参数模型的多高层建筑楼面加速度研究

2023-01-31卢文胜

振动与冲击 2023年2期

樊圆，卢文胜

(同济大学土木工程学院，上海 200092)

对非结构构件进行合理抗震设计的关键在于确定合适的非结构构件地震作用。在实践中，对非结构构件进行抗震设计时，设计荷载均采用等效静力法来计算[1]。各规范[2-4]中的主要参数包括设计地震动加速度峰值、楼面加速度放大(floor acceleration amplification，FAA，楼面加速度峰值/地面加速度峰值)系数、非结构部件反应加速度放大系数、部件状态系数(刚性/柔性)和部件重要性系数等。其中， FAA的取值最大程度地影响非结构构件的抗震设计载荷， FAA进一步乘以构件放大系数即可确定非结构构件加速度相对地面加速度的放大值，是最为关键的参数之一[5]。中国GB 50011—2016规范中FAA最大值取2.0；美国ASCE 7-16规范和欧洲Eurocode 8中FAA最大值取3.0。整体而言，在各国规范中，FAA在结构顶层的取值均在2.0～3.0，楼面最大加速度随所在楼层高度的增大而增大，能够体现结构对地震作用的放大效应[6]。

楼面FAA主要研究方法是通过实测记录进行概率统计，或对某一特定建筑结构进行精细有限元分析。Drake等[7]系统分析了加州150栋房屋在1971年—1994年间的楼面加速度记录并得到了FAA沿结构高度线性分布后，这一公式迅速成为NEHRP及后续各国规范中的非结构构件地震作用分布形式[8]。随着结构强震记录的增加，越来越多的结构响应和规律被记录和分析[9]。一些学者也因此按照不同的结构形式、高度等参数，分别拟合了FAA分布曲线[10-11]在某些高幅值记录下，结构可能的非线性程度、主体结构周期的变化等会显著改变FAA的分布规律[12]。此外，针对某些缺乏地震记录的特定结构形式的单一建筑的模拟研究，也会为FAA取值提供参考依据，例如具备一定耗能能力的摇摆结构的FAA为2.0[13]，也发现一些其他参数对于FAA的贡献，如地震动的扭转分量对FAA的影响可能高达34%[14]，受鞭梢效应影响的结构顶部FAA可达10以上[15]。这些针对特定结构进行的研究为确定FAA的合理范围提供了数据积累，但对FAA受参数影响的规律仍有必要进行进一步的研究。

为研究楼面FAA影响因素和分布规律，本文采用分布参数模型对主体结构进行简化，研究了弯剪刚度比对结构动力特性、模态振型的影响；通过真实结构案例的各阶频率比识别简化模型对应的弯剪刚度比，验证了简化模型的适用性；选用合适的强震动记录数据集，预测了楼面加速度放大系数，回归拟合了可用于楼面加速度预测的公式。

1 分布参数模型

1.1 动力方程

简化的分布参数模型可用于分析结构的动力特性，深入理解体系的机理，因此具有较为广泛的应用[16]。本文选用弯剪梁组合的分布参数模型对主体结构进行简化分析，分布参数模型如图1所示。这一模型及其发展在多层框架、框架-摇摆墙、框架-剪力墙、复合自复位结构等结构的简化中都具有良好的效果[17]。

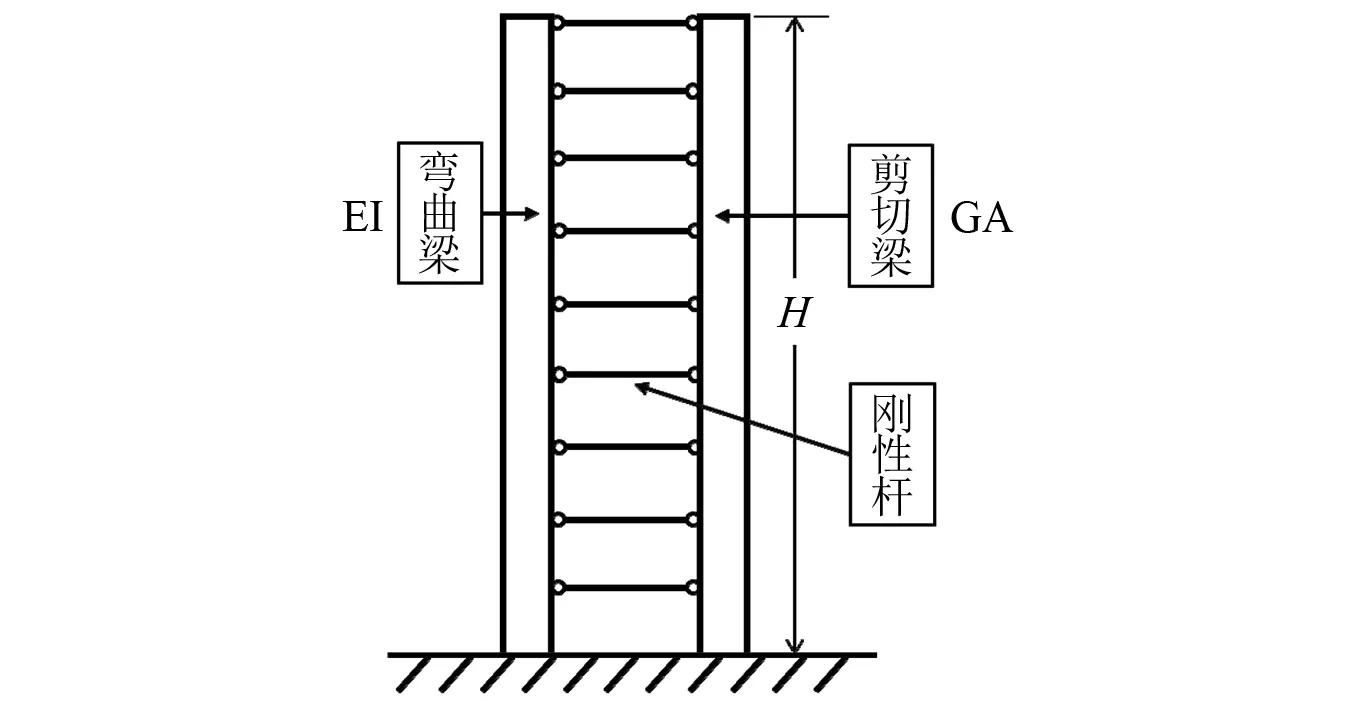
图1 多高层结构的分布参数简化模型Fig.1 Simplified distributed parameter model for multi-story buildings

当遭遇从结构底部的加速度激励输入时，其运动微分方程可以写为[18]

(1)

式中：ρ(x)为模型在任一归一化结构高度x(所在位置高度/结构总高度)处的单位长度质量；u(x,t)为结构在高度x处、时间t时与输入点处的相对位移；ug(t)为从底部输入的地面运动位移时程。若引入结构参数特性随结构变换的函数S(x)，使得EI(x)=EI0S(x)及GA(x)=GA0S(x)，则有

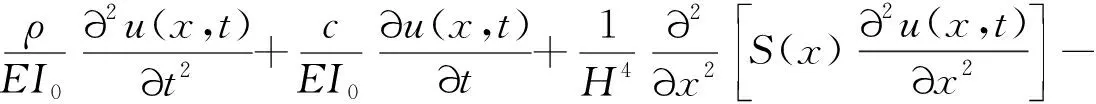
(2)

式中，α0为模型的弯剪刚度比。当α0=0时模型退化为一欧拉梁，当α0→∞时模型可近似看作纯剪切梁。

(3)

对于弹性体系，根据振型叠加法，位移可以由各模态下的位移响应叠加得到

(4)

式中，ui(x,t)为第i阶模态的响应对结构总响应u(x,t)的贡献，其计算方法为

ui(x,t)=Γiφi(x)Di(t)

(5)

式中，Γi为第i阶模态的振型参与系数。对于质量均匀的分布参数模型，其第i阶的振型参与系数为

(6)

(7)

1.2 方程的求解

为计算分布参数系统的动力特性，对于式(2)，考虑在自由振动下公式右侧输入为0。此时，若系统不考虑阻尼，则有对应于无阻尼自由振动的齐次方程

(8)

将式(5)代入式(8)，并进一步考虑结构参数沿结构高度一致的情况，即S(x)在任意高度处取1，通过分离变量法可得两个常微分方程

(9)

(10)

考虑在模型底端位移、转角为0、在顶端弯矩、剪力为0四个边界条件，解得

(11)

(12)

其中，

(13)

且γi和α0满足关系

(14)

1.3 参数影响

由式(11)可知，在结构高度、质量分布确定的情况下，结构频率主要受到α0和γ的影响。而γ和α0满足关系式(14)，因此α0是影响结构频率和振型的主要参数之一。令式(14)左侧为F(γ,α0)，则F(γ,α0)与x轴的第i个交点即为γi的值。图2展示了不同梁柱刚度比α0对γ的影响。图2(b)中可见，γ1的值在1.6～2.0，γ1随α0的增大先增大后减小，其他各解的分布特征与γ1类似。

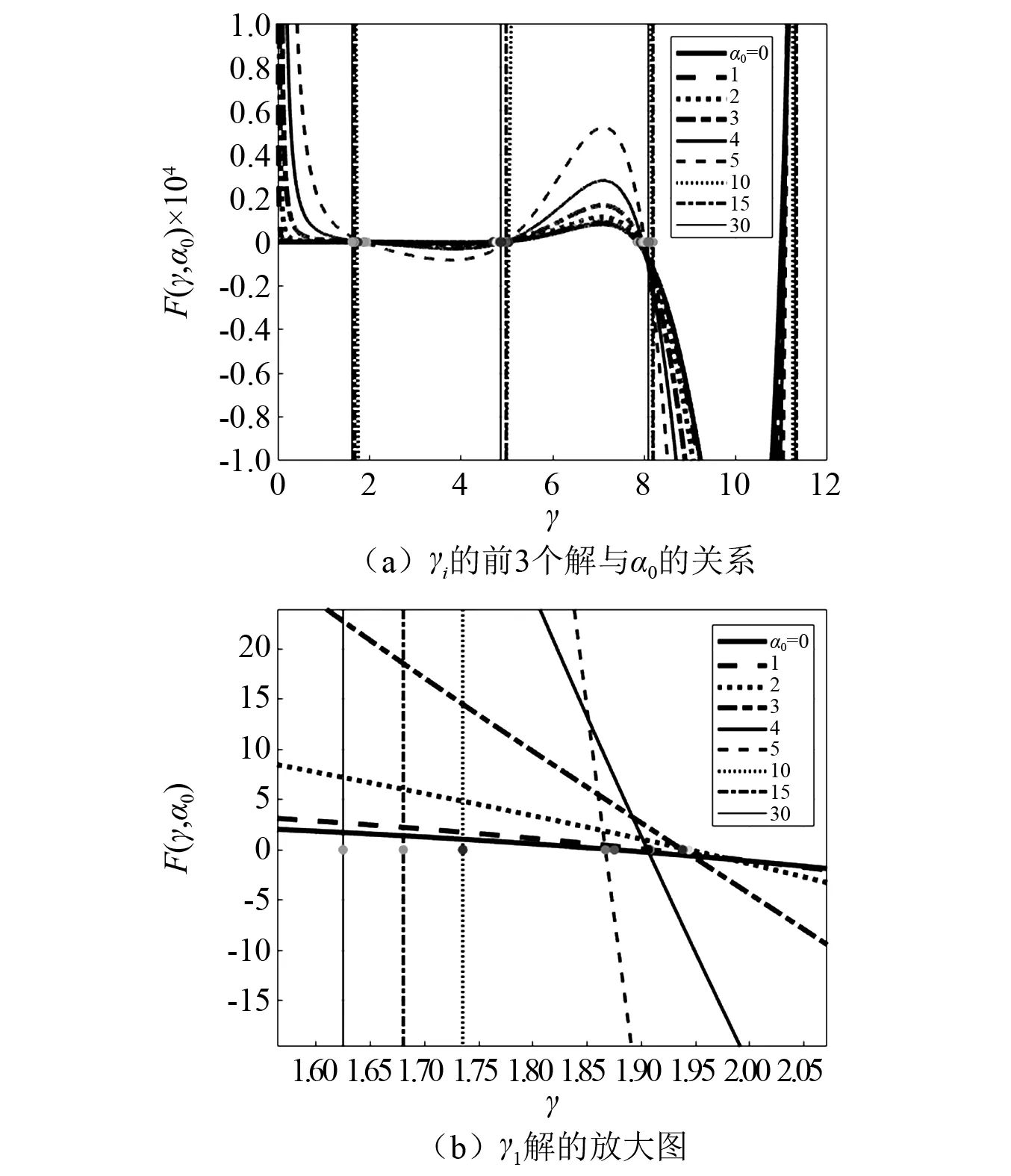
图2 弯剪刚度比α0对γi的影响Fig.2 Influence of α0 on γi

将求解得到的γi和α0代入式(12)，即可得到对应不同α0下的结构模态。图3是不同α0对结构前3阶振型的影响。从图3(a)中可以看到，随着α0的增加，在结构中间高度位置加速度响应逐渐提高，整体曲线形态从上凸转变为下凹，体现了结构从纯弯曲型到弯曲-剪切混合最后到剪切型的响应特征。由图3(b)和图3(c)中可知，随着α0的增加，在结构中间高度处出现振型峰值的结构高度逐渐降低，峰值逐渐提高。整体而言，α0对结构振型的影响较为明显。

图3 α0对结构前3阶振型的影响Fig.3 Influence of α0 on the first three modes

2 模型验证

为验证分布参数模型的可行性，本文选取一栋布设有结构强震观测系统且在历史地震中获取结构响应记录的高层结构，并将模型计算的动力特性和动力响应结果与实测值进行对比。该结构为一栋位于美国洛杉矶的54层钢中心支撑框架结构，强震仪布设在结构的B5、14层、22层、35层、49层和顶层，结构立面和布设位置如图4所示。实测记录来自美国CESMD(Center of Engineering Strong Motion)数据库中数据，为该结构在M6.4 Northridge地震中记录到的结构响应，PGA为0.15g，测得的结构最大楼面响应为0.41g。

图4 台站24602及其记录的响应Fig.4 Station 24602 and its recorded responses

为识别结构的动力特性，对实测数据使用随机子空间算法提取结构的动力特性。随机子空间算法作为一种基于状态空间方程的结构模态识别方法，通过求解系统矩阵特征值与特征向量的方式求解动力特性参数。且由于特征值应呈共轭对的形式存在，可以初步剔除一些错误的识别结果，提升识别准确性。

为将分布参数模型基本动力特性与识别得到的结构特性对比，提出一种基于频率比关系的结构弯剪刚度比识别方法。响应对于某一特定结构，可以通过对结构各阶频率比的识别得到结构的弯剪刚度比α0的近似值。由式(11)可知，对于同一结构，结构高度、等效弯曲刚度、密度等参数相同，则各阶频率与一阶频率的比值可写为式(15)，频率比与α0和γi相关。又因γi由α0根据式(14)求解而来，因此频率比仅由α0决定。因此可采用式(16)中对各阶频率比与实际识别得到的频率比的误差平方和(sum of the squared errors,SSE)并提取使得SSE最小的α0作为结构真实α0的合理近似值。

(15)

(16)

表1展示了结构通过SSI算法识别得到的前三阶频率、阻尼比的实测识别结果和分布参数模型预测结果。图5(a)展示了不同α0下，SSE的变化，并提取得到SSE最小时，α0的值为12.69，该值也处在该结构类型α0值5～20的推测范围中，体现了使用SSE方法对结构α0取值的合理性，图5(b)展示了当α0取12.69时，各阶频率与一阶频率比的情况，可以看出模型的预测结果与真实记录识别结果的匹配较好。图5(c)展示了当α0取12.69时(图6和图7中取值相同)，结构前3阶模态的振型(图中散点)与模型预测振型(图中曲线)的对比，可以观察到而顶部位置存在一定差异。在顶部位置的差异可能是由于实测值中存在顶部鞭梢效应的影响，而模型中无法准确体现这一效应。但整体而言，实测值与预测值在较低结构高度的拟合程度较好，体现出模型能够较好地模拟实际结构的动力特性。

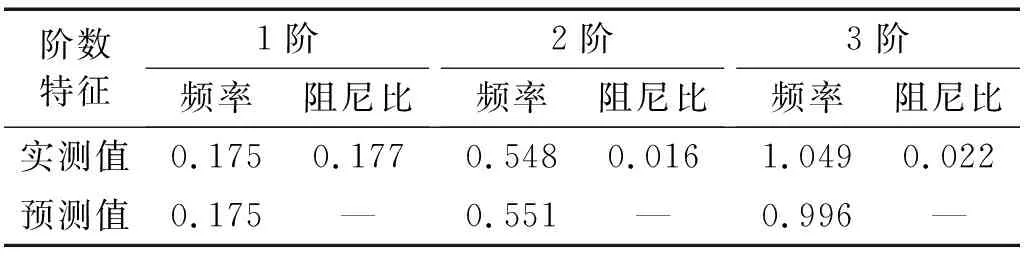
表1 结构前3阶频率、阻尼比识别结果Tab.1 Identification results of the first three modes

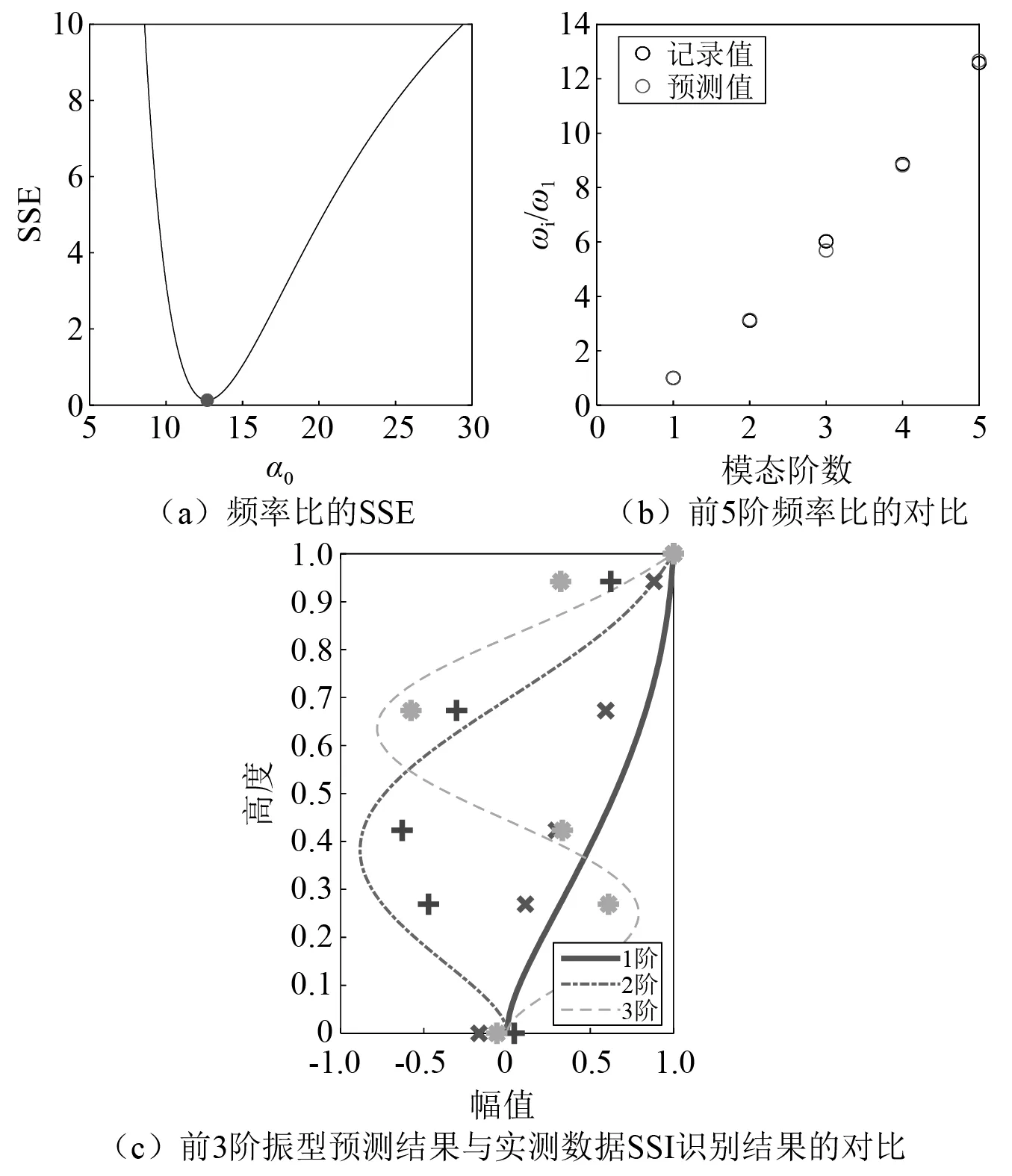
图5 结构弯剪刚度比的识别和频率、振型对比Fig.5 Identification of α0 and comparison of frequencies and modes

进一步将地震记录输入到模型中，计算结构顶层的响应时程。在计算中，阻尼比取2%。可得到结构顶层的响应时程及各阶模态的贡献(见图6(a))，计算得到顶层最大加速度为0.197g。在加速度峰值时刻，各阶的贡献见图6(b)，对全时长而言，加速度响应和各阶加速度贡献的相关系数如表2所示，结果表明1阶对加速度响应的贡献较小，对加速度响应贡献最大的是结构的第2和第3阶，体现了高层结构动力响应受更高阶周期成分的结构动力特征。

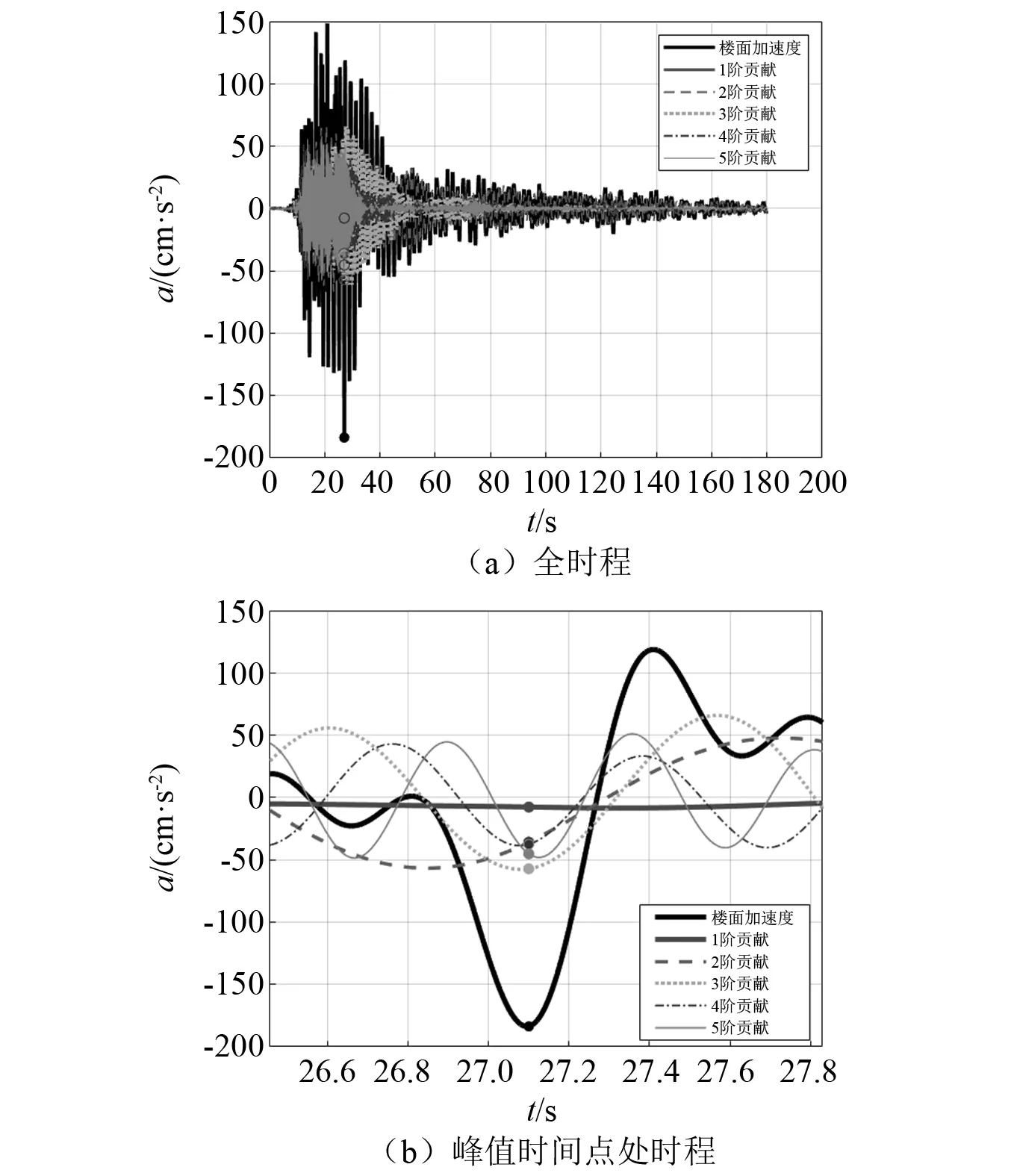
图6 Northridge下顶层加速度时程预测和各阶贡献Fig.6 Estimated roof response and contribution of single modes under Northridge

表2 Northridge顶层时程与各阶时程的相关系数Tab.2 Correlation coefficient between roof response and SDOF responses under Northridge

将顶层加速度实测时程与通过分布参数模型计算得到的预测值进行对比(见图7(a))，实测值的峰值为0.222g，预测值峰值为0.197g，误差为11.26%，且在强震段与实测值的峰值、相位等时程主要特性相符。图7(b)是结构FAA的模型预测值与实测值的对比，虽然实测值的测点较少，但可以观察到实测值在分布上与预测值在各高度处的分布较为一致，对于顶部加速度放大也有较为准确的预测。综合而言，分布参数模型对于楼面响应预测具有可行性和有效性。

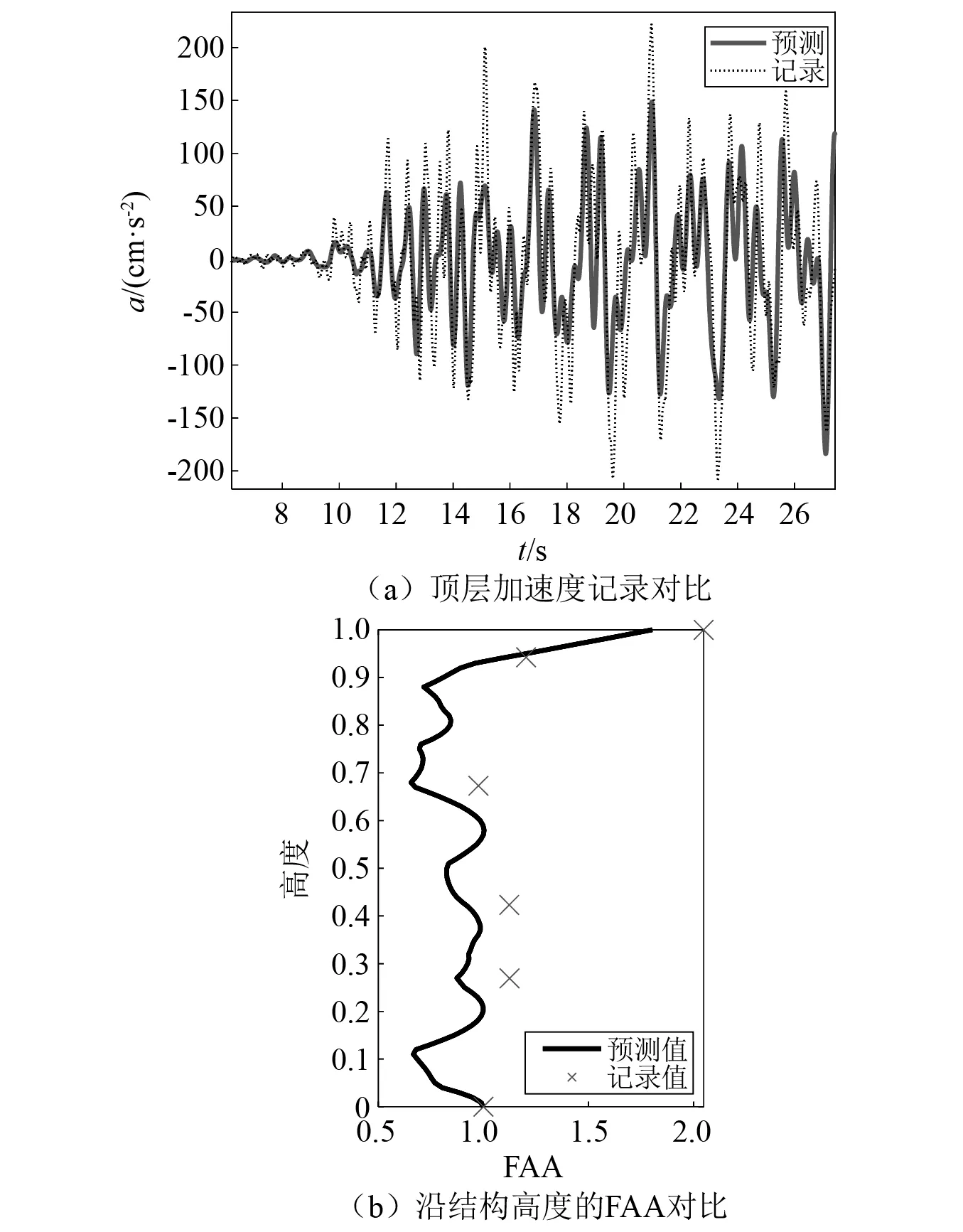
图7 预测值与实际记录的对比Fig.7 Response comparison between estimated and recorded

3 顶层FAA的影响因素

结构周期和结构形式是影响顶层FAA的重要影响因素。基于记录的FAA研究表明，不同结构形式对FAA的影响较大，砌体结构的FAA一般高于钢结构建筑，再高于RC框架建筑。这些建筑形式的差异在结构力学特征上主要体现在刚度、质量、阻尼的分布，而刚度、质量的分布能够被结构的周期、模态所体现。在简化模型中，结构的模态主要取决于α0弯剪刚度比这一参数的贡献。因此研究α0的变化即可体现不同结构侧向抗力体系的FAA变化。常规弯曲型、弯剪混合型、剪切型建筑的α0分别在0～1.5，1.5～5.0及5.0～20.0，且α0在高于30.0时，对结构动力特性的影响较小[20]。因此研究结构形式对FAA影响时，α0取0～30.0为参数范围。

基于典型记录El Centro地震动，研究了顶层FAA的影响因素。图8是基于El Centro记录的顶层FAA与结构周期、α0关系。图8中结果表明，顶层FAA随结构周期的提高整体呈先增大后减小的趋势，在α0=3.2，结构周期T=0.6 s时取得最大顶层FAA为4.86，在α0和T取最大值时取得最小顶层FAA为0.439。FAA随结构周期变化的趋势与输入地震动的反应谱具有很强的相关性，且在多个地震动卓越周期或卓越周期的倍数附近有明显的放大现象。此外，FAA与α0关系密切，在结构的各个周期上FAA随α0的增大而整体减小，减小的速率随结构周期的增加而增加。当结构周期T=1 s时，FAA在α0取30时(顶层FAA为2.74)的值约为在α0取0时(顶层FAA为3.61)的76%。当结构周期T=10 s时，FAA在α0取30时的值仅约为在α0取0时(顶层FAA为1.97)的22%。

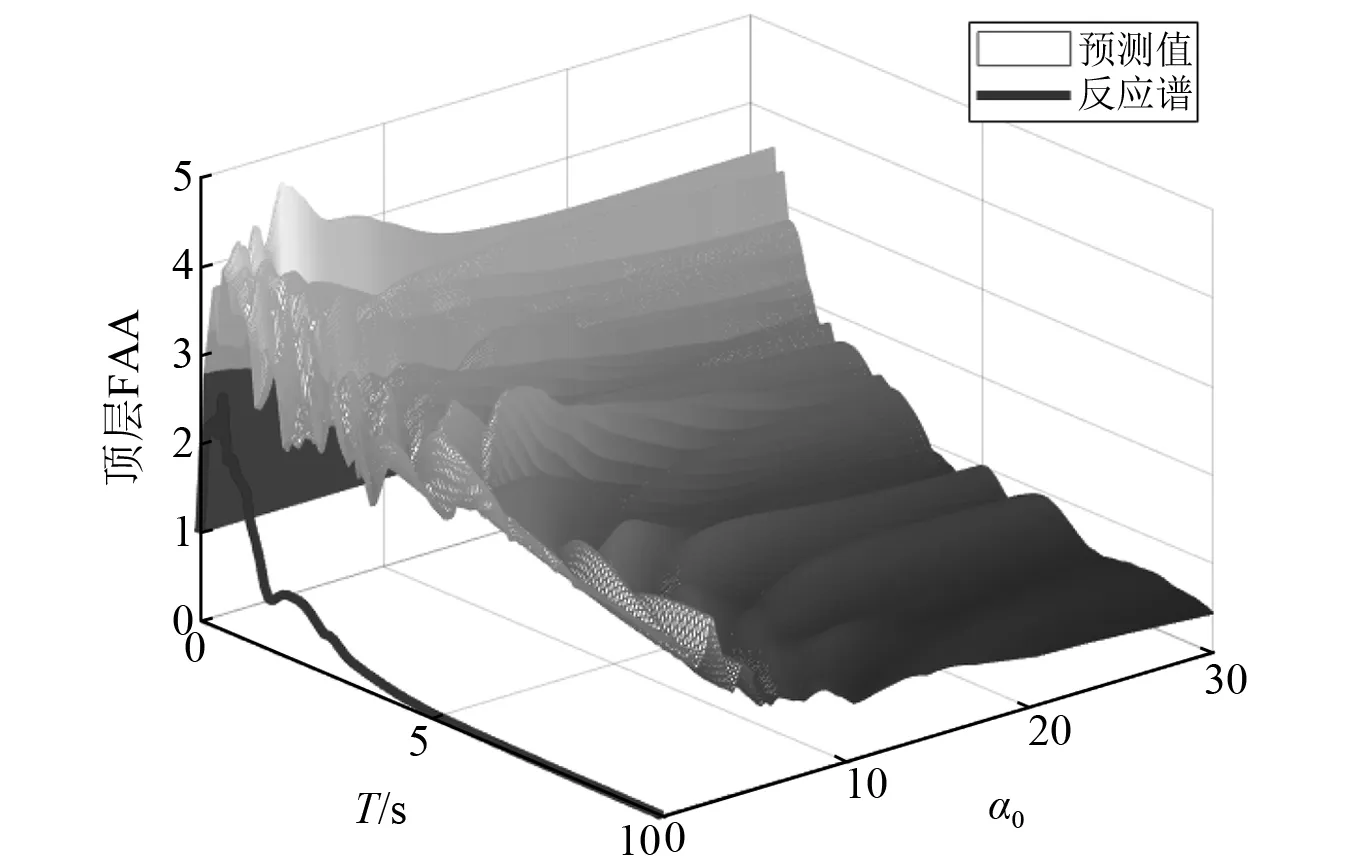
图8 El Centro下的顶层FAA均值与周期、α0的关系Fig.8 Relationship of roof FAA with period and α0 under El Centro

4 数据集和预测结果

4.1 顶层FAA

为研究多条地震记录输入下的结构加速度响应情况，需选用一个包含较多记录的数据集。因此，选用了ATC-63建议的数据集，共包含22组远场和28组近场地震动(共100条单向地震记录)。该数据集在选择时考虑了以下规则：①地震震级在6.5级以上；②震源机制为走滑或逆冲断层；③场地为硬土或岩石，主要选取C类型、D类型的场地记录；④震中距大于10 km。近场地震和远场地震具有不同的破坏特性，需要区别对待；⑤来自同一地震事件的地震动不超过2条；⑥地震动 PGA>0.2g，PGV>15 cm/s；⑦地震动有效周期大于4 s；⑧强震仪安装在自由场地或小建筑的地面。基于上述条件，ATC-63报告中给出 22条远场和28条近场地震动可有效体现地震动的不确定性，对于研究地震作用下楼面加速度的地震动输入提供了合适的数据集。图9为数据集中各记录的归一化加速度反应谱及均值反应谱，对比近场记录，远场记录整体体现出在频率成分更加丰富，以及在反应谱上的更大峰值。

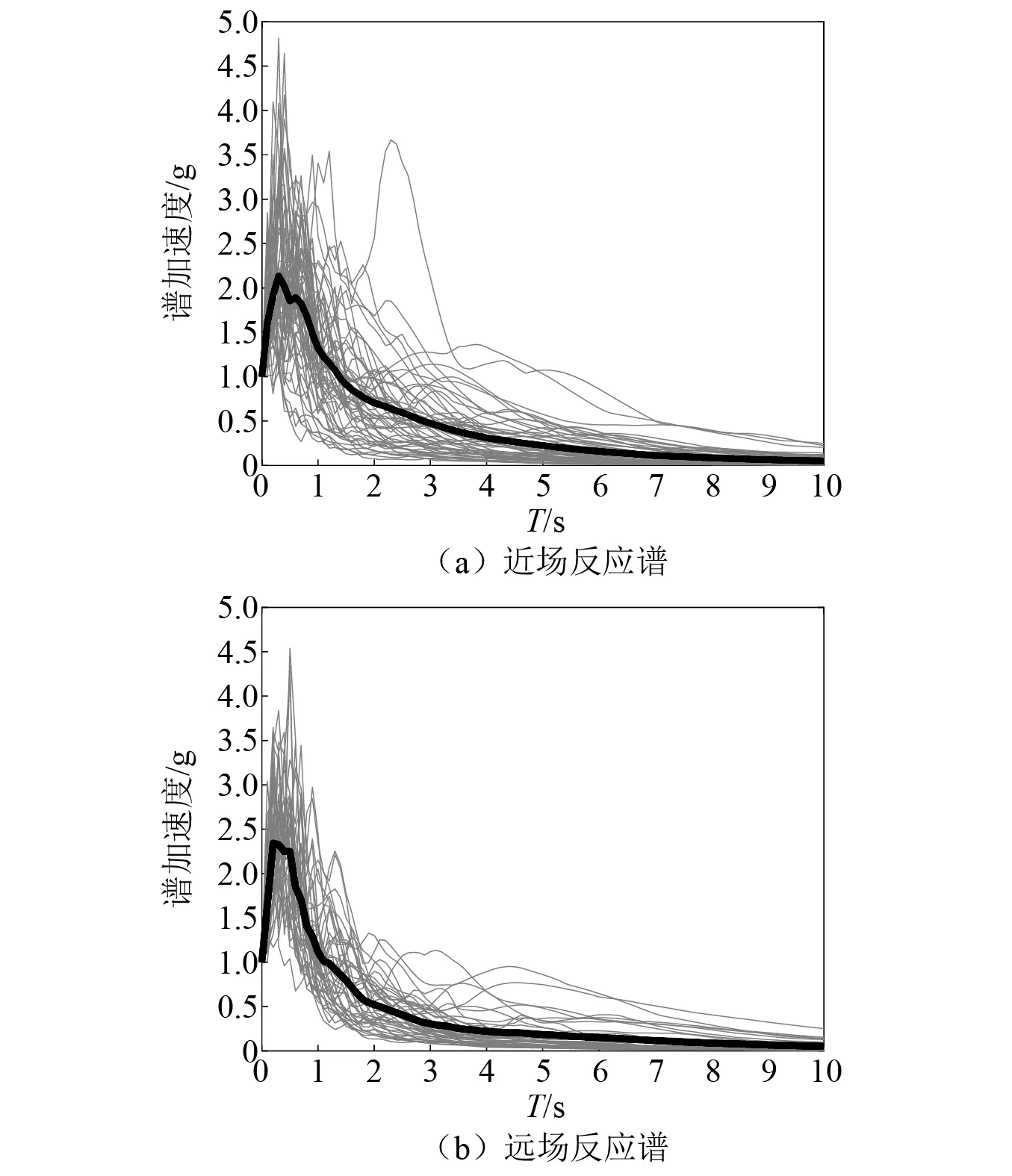
图9 ATC-63数据集加速度反应谱及均值Fig.9 Acceleration spectrum of ATC-63 dataset

图10是基于ATC-63数据集的顶层FAA与结构周期、α0关系，图10中的顶层FAA为各条记录的顶层FAA的平均值。近场和远场数据集的计算结果在顶层FAA随结构周期和α0变化的规律上相似，也与图8的规律一致。近场记录作用下的最大顶层FAA为3.40，最小值为0.51。远场记录作用下的最大顶层FAA为3.80，最小值为0.41。对比图8单一地震作用下的结果，发现顶层FAA的曲面更加平滑，在多个地震动卓越周期或卓越周期的倍数附近的放大现象减弱，仅在α0较小时存在一定的不均匀放大。此外，在结构的各个周期上FAA随α0的增大而较好地线性减小。

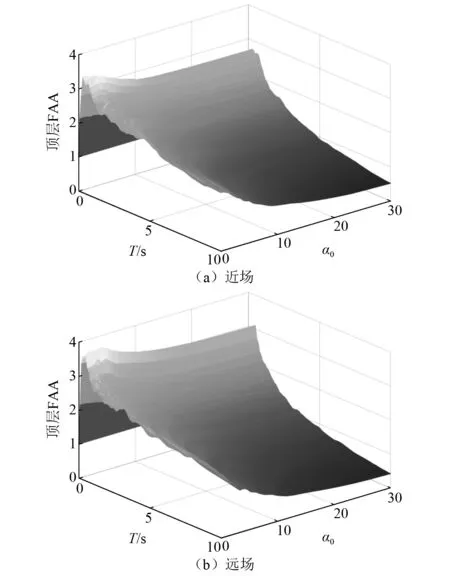
图10 结构顶层FAA均值与周期、α0的关系Fig.10 Relationship of roof FAA with period and α0

对近场记录结果进行拟合，考虑FAA主要受三个物理量的影响：阻尼比ξ、刚度比α0和结构周期T。拟合得到顶层加速度的公式，C(α0)为α0的调整系数，C(ξ)为阻尼调整系数，C(T)为周期调整系数

FAAroof=C(ξ)×C(α0)×C(T)

(17)

式中：C(ξ)主要考虑不同阻尼比下各阶模态对应单自由度体系时程的峰值不同，式(18)与抗规中最大水平影响系数的阻尼调整系数一致，且当C(ξ)<0.55时，取为0.55。

(18)

式(17)中，C(α0)主要考虑不同刚度比α0对FAA的影响。图11(a)中的实际值和拟合结果显示在近场地震作用下，FAA与α0的斜率与结构周期T呈较好的线性关系，可以用结构周期T来描述FAA与α0的斜率，即

(19)

式(17)中，C(T)主要考虑不同结构周期T对FAA的影响。图11(b)中在近场地震作用下，FAA随结构周期的变化大致可分为3段，即在短周期的上升段和平台段，以及在长周期的下降段。分别对各段进行直线或指数拟合，得到FAA与T的经验关系

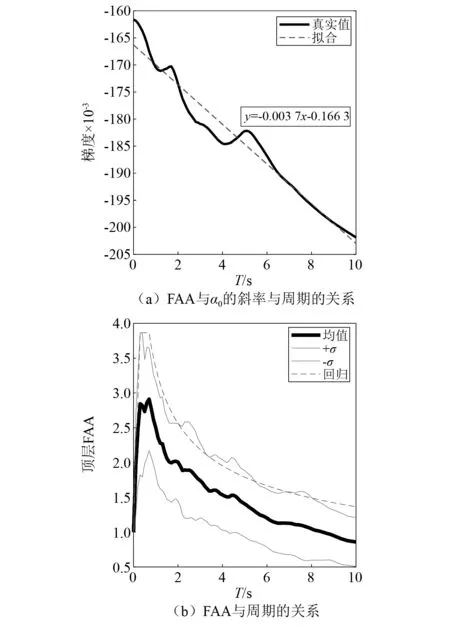
图11 近场记录作用下FAA的影响因素(α0=10)Fig.11 Influencing factors of FAA under near field records(α0=10)

(20)

远场地震动作用下，当α0=10时的结构顶层FAA与周期T的关系如图12(a)所示；FAA与α0的斜率与周期T的关系如图12(b)所示。顶层FAA的峰值较近场地震动作用下的顶层FAA值更高，且峰值对应的结构周期更长，这一结果也与近远场记录的反应谱一致，体现出远场记录具有更大的地震动潜在破坏势。

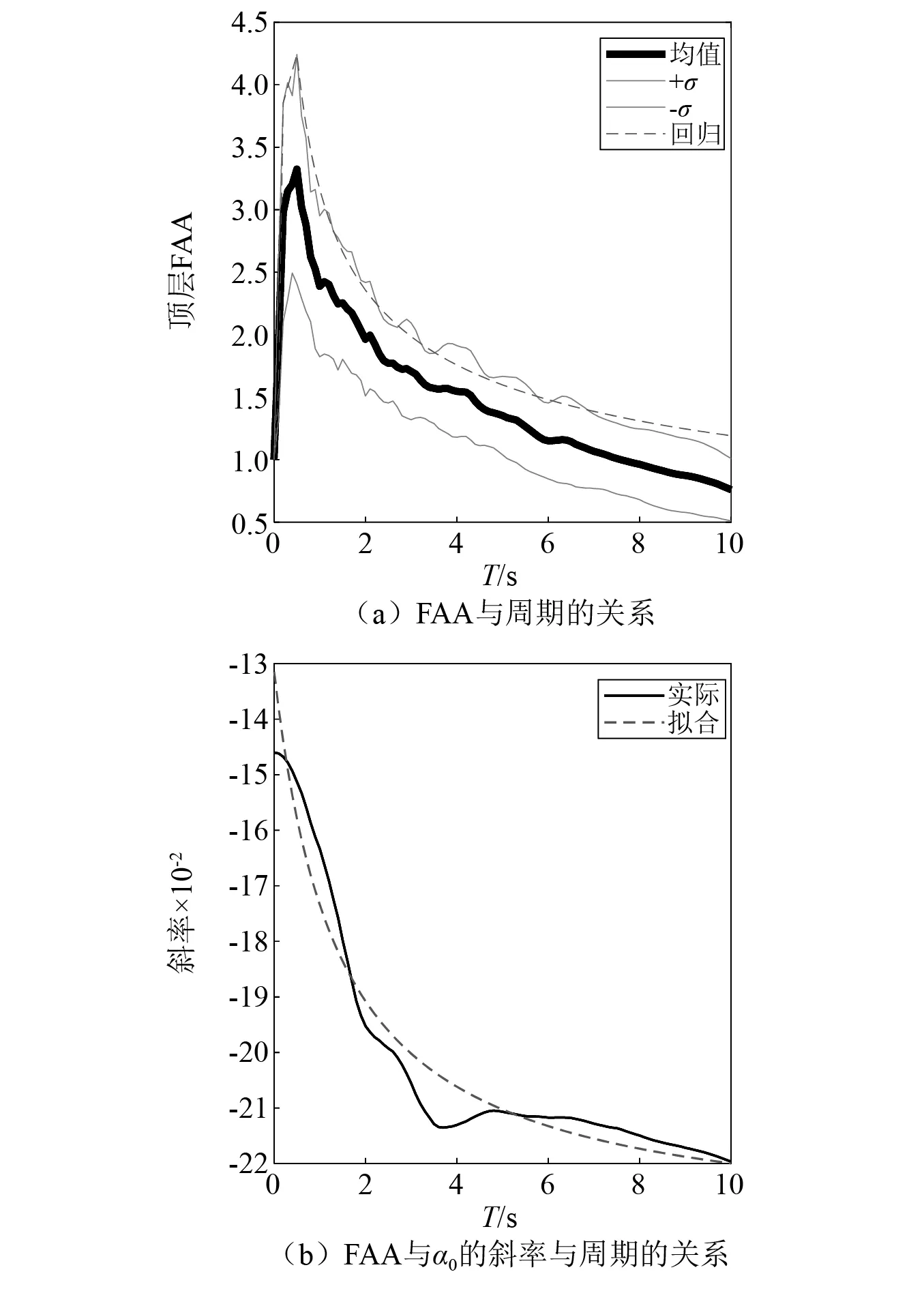
图12 远场记录作用下FAA的影响因素(α0=10)Fig.12 Influencing factors of FAA under far field records(α0=10)

在远场地震作用下，FAA与α0的斜率与结构周期T呈较好的反比例关系，可以用结构周期T来描述FAA与α0的斜率，即

(21)

同时，在远场地震作用下，FAA随结构周期的变化大致可分为3段，即在短周期的上升段，以及在长周期的下降段。分别对各段进行直线或指数拟合，得到FAA与T的经验关系

(22)

4.2 沿楼层高度FAA的分布

受到刚度分布、质量、材料等的影响，建筑结构在受到水平作用力时会表现出不同的变形特征：砌体结构、剪力墙结构等主要表现为弯曲型；多高层钢筋混凝土(RC)框架、钢框架等结构主要表现为剪切型；钢筋混凝土框剪、钢框架-中心支撑、钢框架-偏心支撑等主要表现为弯剪型。结构沿楼层高度的FAA形态受到结构主要参数的显著影响，因此分别研究结构弯剪刚度比α0和结构周期T对沿楼层高度FAA分布的影响。

图13(a)～图13(d)是不同α0下FAA沿楼层高度分布与结构周期T的关系。当α0较小时，以图13(a)为例，FAA随楼层高度呈现先增大后减小，最后再顶部0.8～0.9倍结构高度以上显著增大的趋势。随着周期T的增大，结构中部FAA减小，且增大的幅度有所减少，顶部放大的逐渐减少；当α0较大时，结构0.8～0.9倍结构高度以上部分加速度放大的趋势与α0较小时相似，但结构中低楼层由于受到高阶振型的影响呈现一定的波动，但楼层FAA整体仍呈与结构高度的较好线性特征。随着周期T的增大，结构中部FAA不断减小，特征与α0较小时相一致。

图13 不同α0下FAA沿楼层高度的分布与T的关系Fig.13 Relationship of FAA along height with T under different α0

对同一α0下同一结构高度处不同周期T的FAA取均值，得到FAA在各楼层高度处的均值与α0的关系(如图14(a)所示)。由图14(a)可知，当α0增加时，结构中下部分的FAA降低，而顶部的FAA提高。为定量表达结构弯剪刚度比α0对FAA分布的影响，依据FAA随结构高度先增大后减小的趋势，使用分段线性方法进行拟合。将FAA分布曲线(如图14(b)所示)分为三段直线，直线的四个端点从上至下分别为(FAAroof，1)，(FAAh1,h1)，(FAAh2,h2)，(1,0)。点(FAAh1,h1)为FAA从顶层向下首次增大的点，点(FAAh2,h2)为FAA从底层向上(不包括0高度位置)首次减小的点。为表达中间两个端点在放大系数和高度上的影响，引入点(FAAs1,h1)和点(FAAs2,h2)分别为连接点(FAAroof，1)和点(1,0)的直线上对应h1和h2高度的点，并定义

(23)

Cα0,21=h1,Cα0,22=h2

(24)

则Cα0,11，Cα0,12可分别表达两端点的放大系数，Cα0,21，Cα0,22可分别表达两端点的高度。图14(c)可观察到Cα0,11与周期T近似服从线性关系，因此用一次关系拟合Cα0,11。图14(d)可观察到Cα0,12与周期T的关系为先增大，后震荡减小，因此在较短周期用平台段包络，在衰减段用一次关系拟合，再用平台段对长周期进行拟合。图14(e)可观察到Cα0,21在全周期中的偏差较小，最小值0.84，最大值0.88，因此用全周期的平均值常数体现Cα0,21。图14(f)可观察到Cα0,22随周期先减小后保持恒定，因此使用三段一次关系拟合Cα0,22。四个描述FAA形态的参数的拟合见式(25)～式(28)。

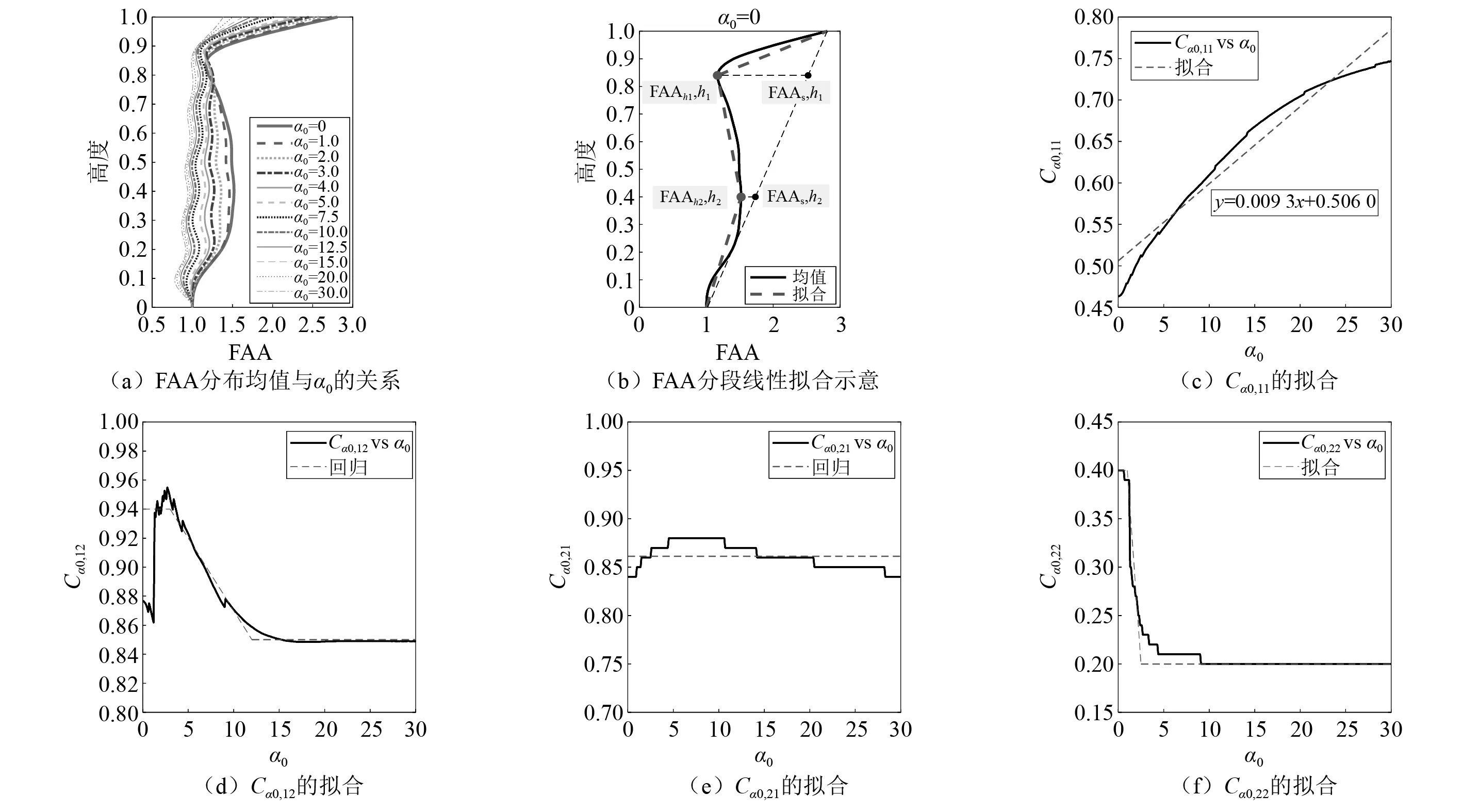
图14 FAA与α0的关系拟合Fig.14 Regression of FAA with α0

Cα0,11=-0.009 3α0+0.506 0

(25)

(26)

Cα0,21=0.861 3

(27)

(28)

图15(a)～图15(d)各分图是不同周期T下FAA沿楼层高度分布与结构周期α0的关系。当T较小时，以图15(a)为例，FAA随楼层高度变化的规律与结构一阶振型相似，随α0的增大曲线形态由上凸变为下凹。图15中同样可以清晰看到在结构顶部的放大效应，同一T下，出现拐点的高度相对稳定，但随着T的变化拐点高度逐步增大。当T较大时，FAA的分布形态与图13中α0较大时相似，均为在顶部位置有显著放大，在中低层位置近似保持线性关系。

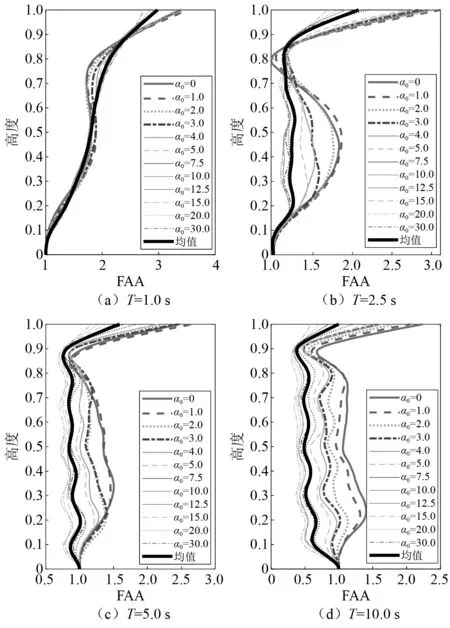
图15 不同T下FAA沿楼层高度的分布与α0的关系Fig.15 Relationship of FAA along height with α0under different T

对同一周期T下同一结构高度处不同α0的FAA取均值，得到FAA在各楼层高度处的均值与T的关系(如图16(a)所示)。由图16(a)可知，当T增加时，结构的FAA先增大后减小，且在不同T下，FAA均能保持沿结构高度增加而线性增加的趋势。相似的，为定量表达周期T对FAA分布的影响，依据FAA随结构高度先增大后减小的趋势，使用分段线性方法进行拟合。将FAA分布曲线(如图16(b)所示)分为两段直线，直线的三个端点从上至下分别为(FAAroof，1)，(FAAh,h)，(1,0)。点(FAAh,h)为FAA从顶层向下首次增大的点。为表达中间两个端点在放大系数和高度上的影响，同样引入点(FAAs,h)为连接点(FAAroof，1)和点(1,0)的直线上对应h高度的点，并定义