颗粒阻尼吸振器对轧机辊系减振特性的研究
2023-01-31徐慧东和东平王义平任超然
王 明, 徐慧东, 和东平, 王 涛, 王义平, 任超然
(1. 太原理工大学 机械与运载工程学院,太原 030024; 2. 先进金属复合材料成形技术与装备教育部工程研究中心,太原 030024)
随着综合国力的提升,我国对高质量钢材的需求量逐渐增加,板带轧制生产作为目前主要的钢铁成材工艺,面临着诸多关键性的技术难题。其中,板带轧制过程中设备发生的多种形式的非线性振动制约着轧制生产高速化、高效化和连续化,成为亟需解决的关键性问题,越来越受到国内外学者的重视[1-3]。钟掘等[4]分别对轧机振动中的界面耦合机理与机电耦合机理进行了分析,对轧机的稳定性控制具有一定的指导意义;王桥医等[5]研究了连轧机多机架耦合振动系统的动力学特性,结果表明厚度不均匀的带材会引起轧辊振动,通过降低拾取卷筒速度可以使连轧机更稳定;王鑫鑫等[6]提出利用扩张状态观测器抑制轧机振动的方法,该方法可以有效抑制多种情况下的轧机振动;孙韵韵等[7]研究了轧制界面的粗糙形貌对轧辊动力学特性的影响,为轧机抑振提供了有效的理论参考;Zheng等[8]采用Riccati传递矩阵法及有限元法分析了不同稳定性的四辊轧机的振动特性,认为稳定的四辊轧机中多种形式的振动能够得到有效控制;米凯夫等[9]验证了小波变换和分形技术都能有效识别轧机的振纹振动,为实现轧机振动的预测提供了理论保证;闫晓强[10]通过应用二阶扭振抑制器并对自动辊缝控制(automatic gage control, AGC)参数进行优化,有效地抑制了轧机机电液耦合振动现象。
对于轧机振动的控制,目前主要有主动控制和被动控制两种。主动控制是通过寻找振动原因,并提出相应的对策来控制轧机的振动;被动控制方法是通过改变某些构件的参数来增加系统的阻尼或在适当部位附加子系统以消耗主系统的振动能量[11]。动力吸振器则属于被动控制的一种,它主要由质量、弹簧和阻尼元件组成。Hermann[12]最早提出了动力吸振器,为了抑制船体的摇摆,Frahm设计了一个能够抑制主系统共振的水箱。经过百余年的发展,动力吸振装置衍生出了多种形式,从单纯的机械式动力吸振器(dynamic vibration absorber,DVA)发展为机、电、磁、液等耦合式吸振器[13],整体上可分为主动式、半主动式、被动式三大类,并成功地应用于航空航天、机械、土木工程等领域。而由于被动式吸振器结构简单、且成本较低,同时具有不错的结构振动抑制效果,因此在实际工程中应用最为广泛[14]。
传统的单质量块被动式动力吸振器只有在吸振器本身的固有频率、外界激励频率以及受控对象的振动频率三者相同时才能发挥较好的减振效果,且吸振器的各个参数一经设定就无法改变,然而在工程实际中,外界激振频率大多都在一定范围内往复变化,当三者频率不同时,吸振器的减振效果就会严重降低[15],因此,为了增加传统的被动式动力吸振器的减振带宽,一种新型的被动振动控制技术——颗粒阻尼(particle damping,PD)技术逐渐受到研究者们的关注。Meyer等[16]通过研究颗粒阻尼器在不同基本结构特征频率下的阻尼特性,提出对于高本征频率的系统,使用粒径小的颗粒抑振效果比较好,且不同的特征频率的最佳填充率也不同;Zhang等[17]采用离散单元法(discrete element method,DEM)模拟了封闭容器中颗粒在垂直振动作用下的阻尼行为,首次提出一种颗粒阻尼效果的可视化评价方法;Xiao等[18]将颗粒阻尼器应用于矿用自卸车驾驶座椅的减振,通过仿真分析以及试验得出了最优的颗粒阻尼方案。
本文在目前专家学者对PD的研究基础上,根据轧机的结构以及工作特点,提出一种应用于轧机辊系的新型多自由度颗粒阻尼吸振器,并对其减振性能展开研究。
1 振动控制目标与颗粒阻尼吸振器设计
1.1 振动控制对象及可行性分析
本文以图1所示的二辊静定轧机的上工作辊为振动控制对象,研究颗粒阻尼吸振器各参数对工作辊振动控制效果的影响。

图1 二辊静定轧机Fig.1 Two-high statically determinate rolling mill
PD技术一般也称为非阻塞性颗粒阻尼技术(non-obstructive particle damping, NOPD),是在振动控制目标结构上加工出孔洞或者外附封闭空间的颗粒容器,并填充一定数量、尺寸的颗粒阻尼材料,当主结构在外界激励下发生振动时,致使颗粒与颗粒、颗粒与容器壁之间产生碰撞与摩擦,从而转移与耗散振动能量,达到抑制主振系统振动的目的[19]。
PD技术可在高温、低温、辐射等恶劣的环境中发挥作用,并且具有较宽的减振频带[20-21],在0~5 000 Hz的频率范围内都有一定的减振效果[22]。而轧机辊系主要会出现两种垂直振动现象:一类是三倍频振动,其振动频率主要集中在150~250 Hz[23];另一类是五倍频振动,其振动频率主要集中在500~700 Hz[24]。因此将颗粒阻尼技术应用于轧机辊系振动的控制具有可行性。
1.2 颗粒阻尼吸振器设计
由于轧机上工作辊为轴类零件,因此吸振器主体定为环形结构,同时考虑到结构尺寸、空间位置、方便安装、拆卸及调试等方面,设计了一种颗粒阻尼吸振器,其三维结构如图2所示。在轧机上的安装位置如图3所示。

图2 颗粒阻尼吸振器三维结构Fig.2 Three-dimensional structure of particle damping vibration absorber

图3 吸振器在轧机上的安装位置Fig.3 Installation position of vibration absorber
图2中质量外环与内环均为可拆分结构,质量外环与内环通过刚柔耦合吸振组件连接,内环通过轴承安装在上工作辊上。其中刚柔耦合吸振组件共有10组,每组包括4个完全相同的弹簧、4个完全相同的橡胶以及一个颗粒容器。通过改变颗粒容器内颗粒数量或刚柔耦合吸振组件的数量便可以调整颗粒阻尼的大小。
2 带有颗粒阻尼吸振器的轧机辊系主共振特性分析
2.1 带有颗粒阻尼吸振器的轧机上工作辊动力学建模
为了明确颗粒阻尼的抑振效果,建立如图4所示的带有颗粒阻尼吸振器的轧机上工作辊四自由度模型。图4中:m1为轧机上工作辊、轴承及吸振器内环的等效质量;x1为等效质量m1的振动位移;m2为十组刚柔耦合元件中颗粒容器的等效总质量;ma为颗粒容器内颗粒群的等效总质量;mb为颗粒群中发生跳动并产生阻尼作用颗粒的等效总质量;mc为颗粒容器及颗粒群中未发生跳动颗粒的等效总质量;x2为等效总质量mc的等效振动位移(当系统发生颤振时,可能只有部分颗粒之间、颗粒与容器壁之间发生相对运动,从而形成颗粒阻尼);x4为等效总质量mb的等效振动位移;m3为吸振器外环的质量;x3为质量m3的振动位移;c1为上工作辊与轧件之间的等效阻尼;k1和k′1为上工作辊与轧件之间的等效线性刚度和非线性刚度;k2为颗粒容器与内环之间所有弹簧的等效刚度;k3为颗粒容器与吸振器外环之间所有弹簧的等效刚度;c2为颗粒容器与内环之间所有橡胶的等效阻尼;c3为颗粒容器与吸振器外环之间所有橡胶的等效阻尼;k为十组刚柔耦合元件中所有发生跳动的颗粒所产生的等效刚度;c为所有发生跳动的颗粒所产生的等效阻尼;近似认为轧辊受到周期性的外部激励Fcos(ωt)。建立系统的动力学方程为

图4 装颗粒阻尼吸振器的系统四自由度模型Fig.4 Four-degree-of-freedom model of the system with particle damping vibration absorbers
(1)
2.2 带有吸振器的轧机上工作辊主共振响应分析
2.2.1 系统主共振响应求解
对于非线性振动方程,只有极少数的方程可以求得精确解,大多数情况下只能通过近似方法进行求解。常用的近似解法包括谐波平衡法、正规摄动法、林滋泰德-庞加莱法、平均法、多尺度法、渐进法等[25-26]。本文采用多尺度法对振动系统进行求解。
将式(1)进行化简,得到
(2)
其中,
将式(2)右边各项冠以小参数ε得
(3)
其中,
δ1=εδ10,δ2=εδ20,δ3=εδ30,δ4=εδ40,δ5=εδ50,
δ6=εδ60,γ1=εγ10,γ2=εγ20,γ3=εγ30,γ4=εγ40,
γ5=εγ50,γ6=εγ60,γ7=εγ70,k″1=εk10,F0=εF10
引入不同尺度的时间变量
T0=t,T1=εt
对时间t进行微分并忽略ε的高阶小量有
(4)
式中,Dn=∂/∂Tn,(n=0,1),令
(5)
将式(5)代入式(3),分别令方程两端小参数ε的0次幂及1次幂系数相等,得到各阶近似的线性偏微分方程组
(6)
(7)
将零次近似方程式(6)的解表示为复指数形式
(8)
代入一次近似方程式(7)的右边得到
(9)
考虑到系统主共振情况,ω10接近ω,ω10远离ω20,假设ω=ω10+εσ,其中σ表示轧机上工作辊的频率调谐因子。代入式(9)中,并消除系统中的永年项,得到
(10)
为了方便求解式(10),将复函数A1,A2,A3,A4写为指数形式
A1=0.5aeiφ1,A2=0.5beiφ2,
A3=0.5ceiφ3,A4=0.5deiφ4
式中,a,b,c,d,φ1,φ2,φ3,φ4为时间T1的函数,同时令θ=σT1-φ1。
将A1,A2,A3,A4,θ代入式(10)得
(11)
将式(11)的实部与虚部分离得到
(12)
(13)
2.2.2 仿真分析
将式(13)转化为
z3+λz2+μz+ρ=0
(14)
式中:μ为分岔参数;λ,ρ为开折参数;z=a2。
其中,

(15)
根据奇异性理论[27],式(15)为GS范式z3+μz的普适开折表达式,奇异点为余维2的叉形点,此时:
系统的分岔点集
B={ρ=0}
系统的滞后点集
系统的双极限点集
D=∅
系统的转迁集
∑=B∪H∪D
在MATLAB环境下进行仿真分析,得到如图5所示的转迁集区域。图5中,曲线将系统的开折平面分割成4个区域(Ⅰ,Ⅱ,Ⅲ,Ⅳ),仿真得到不同区域和临界点的拓扑结构图如图6所示。

图5 系统的转迁集Fig.5 System transition set
通过分析图6中的局部分岔性态,可以得到系统全局分岔性态,控制开折参数落在较稳定的区域,从而提高轧制过程的稳定性。当开折参数落在原点O及分岔集B+和B-时,系统不稳定区域较大(即一个分岔参数μ对应多个z的多值区域较大);当开折参数落在滞后集H+和H-时,分岔参数处于1.2左右时系统将发生滞后现象;当开折参数落在区域Ⅰ和区域Ⅲ时,系统的稳定区域较大;当开折参数分别由区域Ⅰ和区域Ⅲ越过滞后集H+和H-进入区域Ⅱ和区域Ⅳ时,分岔参数处于1.3~1.9时系统将发生跳跃现象,导致系统产生明显的振动。因此,在实际工程中需要尽量控制轧机各个参数使开折参数λ和ρ处于区域Ⅰ和区域Ⅲ内,进而提高轧制过程的稳定性。
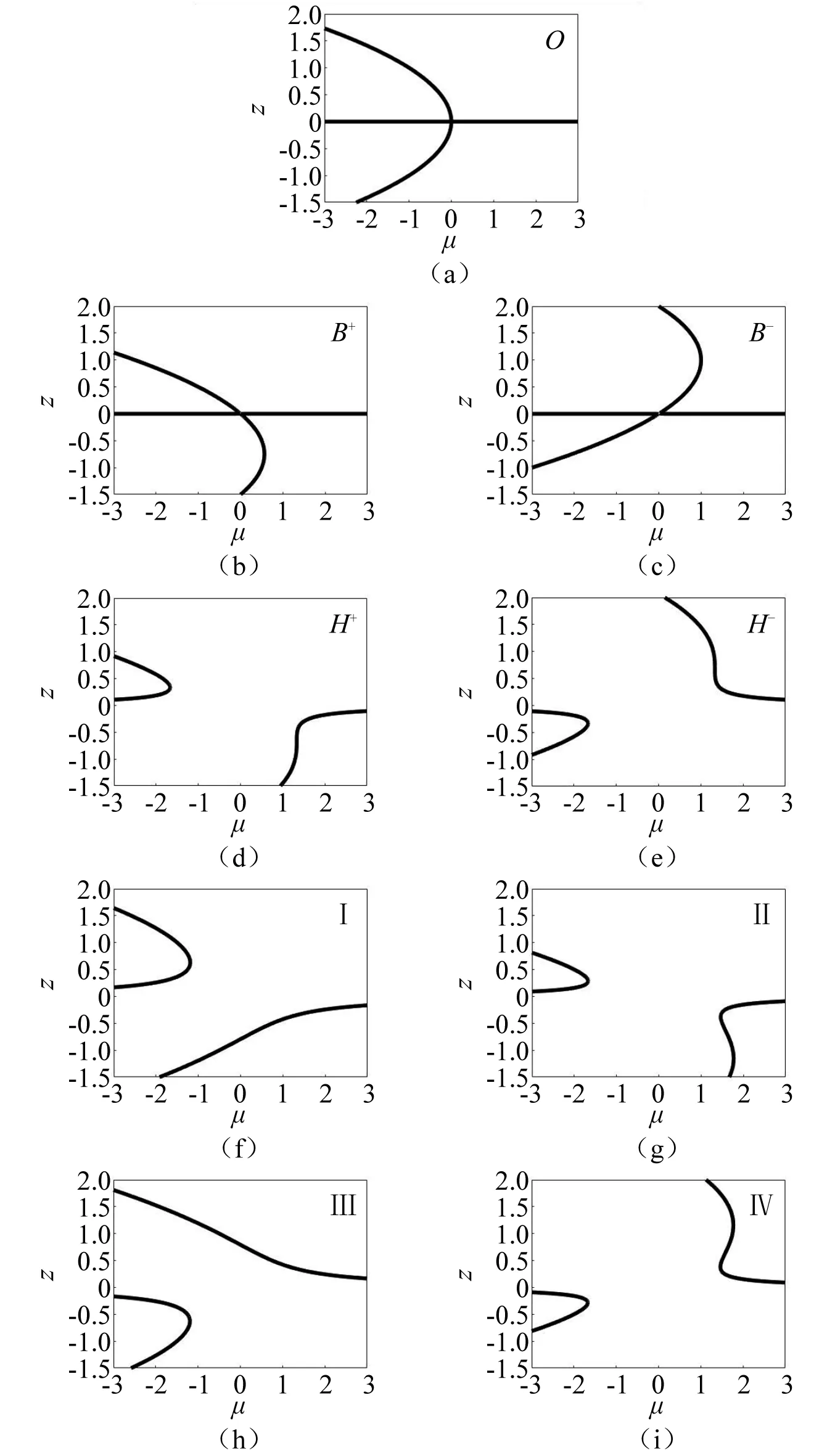
图6 系统拓扑结构图Fig.6 System topology diagram
为了明确多自由度颗粒阻尼吸振器抑振效果,对未装吸振器及装了吸振器之后的轧机上工作辊振动的时域曲线、相图以及频谱曲线进行仿真分析。为了便于相互验证,本文仿真与试验中每个颗粒容器均填充500颗钢珠,填充率约为30%。钢珠各参数如表1所示。

表1 钢珠参数Tab.1 Steel ball parameters
假设50%的颗粒产生阻尼作用,要对该部分颗粒群的整体等效刚度及等效阻尼进行精确分析是相当困难的,因此将跳动的多颗粒等效为单颗粒进行研究。本文根据文献[28]中的等效简化原则进行计算。等效后的单钢珠颗粒半径为13.59 mm。
颗粒碰撞(法向)和摩擦(切向)的等效刚度和阻尼系数计算公式如下:
法向刚度系数
切向刚度系数
法向阻尼系数
切向阻尼系数
式中:α为碰撞颗粒的法向叠合量,本文取1×10-7m;e为钢珠的碰撞恢复系数,文献[29]中通过试验测得两钢珠的碰撞恢复系数值约为0.544。计算可得:
法向刚度系数
kn=1.5×107N/m
切向刚度系数
kt=2.3×107N/m
法向阻尼系数
cn=415.9 N·s/m
切向阻尼系数
ct=515.0 N·s/m
在颗粒群的实际工作过程中,碰撞和摩擦一般是同时存在的,取综合刚度系数k=3.8×107N/m,综合阻尼系数c=930.9 N·s/m。
则系统各参数的仿真取值如表2所示。

表2 带有吸振器的振动系统仿真参数表Tab.2 Simulation parameter table of vibration system with vibration absorber
图7为振动系统时域曲线,可以看到未装颗粒阻尼吸振器时,系统在8 s左右达到稳定状态,安装颗粒阻尼吸振器后系统在5 s左右就达到了稳定状态,且稳定后的振幅降低了23%左右。图8为振动系统相图响应曲线,可以看出,装阻尼器之前系统的稳定状态区域较宽,安装了阻尼器之后系统的稳定状态区域更为收敛,且振动位移及振动速度都相对减小。因此颗粒阻尼吸振器能够抑制轧机上工作辊的垂直振动,提高轧制过程的稳定性。

图7 安装吸振器前后系统时域曲线Fig.7 System time domain curve before and after installation of vibration absorber
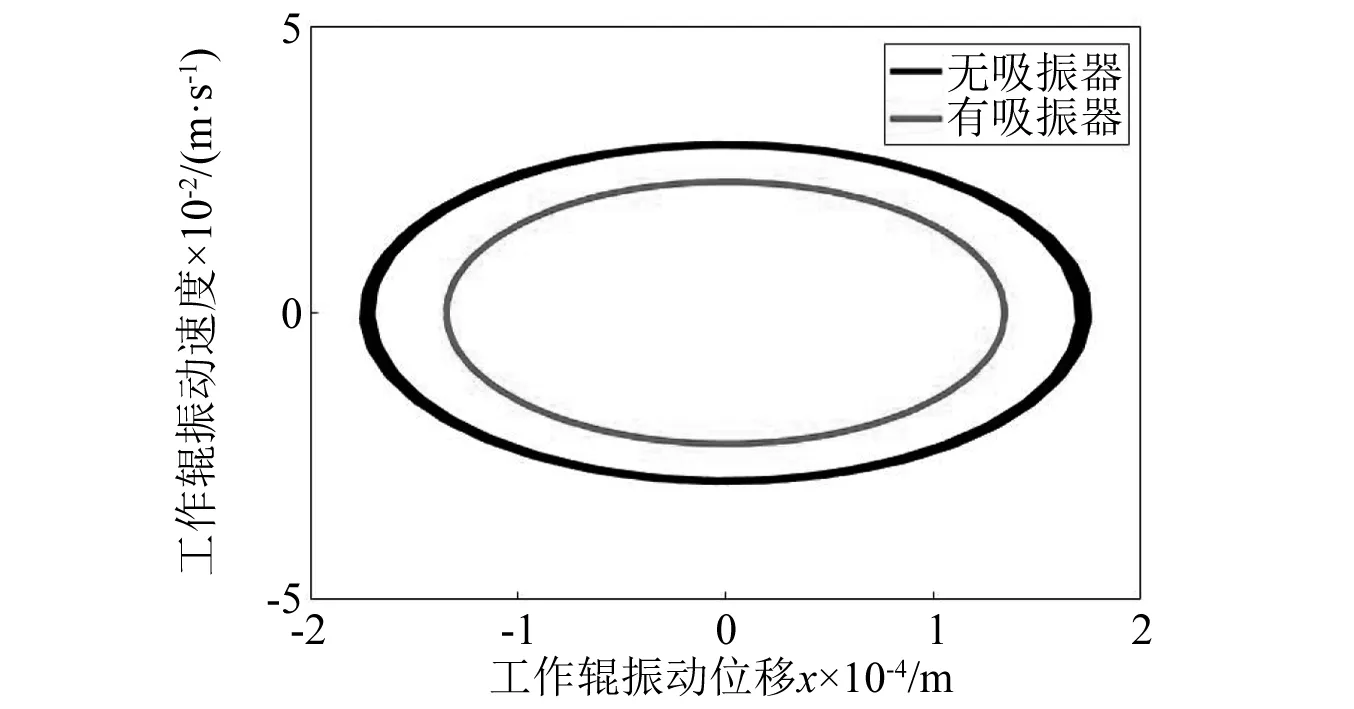
图8 安装吸振器前后系统相图Fig.8 System phase diagram before and after installation of vibration absorber
图9为振动系统的频谱响应曲线,通过对比可以发现,振动系统包含两个共振频率,分别为280 Hz左右的主共振频率及75 Hz左右的谐振频率,安装颗粒阻尼吸振器之后系统的主共振峰值及谐振峰值都有明显降低。进一步证明了颗粒阻尼吸振器对轧机上工作辊具有良好的抑振效果。

图9 安装吸振器前后系统频谱曲线Fig.9 System spectrum curve before and after installation of vibration absorber
通过改变轧机上工作辊非线性刚度参数k10、激励力F、颗粒阻尼吸振器等效刚度系数k2、等效阻尼系数c2可以得到各参数对主共振幅频响应的影响,如图10所示。

图10 各参数的主共振幅频响应曲线Fig.10 Main common amplitude frequency response curve of each parameter
由图10(a)可知,由于轧机非线性刚度的存在,会引起主共振峰偏移,随着非线性刚度系数的增加,偏移量也逐渐增加;由图10(b)可知,随着激励力的增加,系统的主共振峰峰值迅速增加,且共振域也明显增加;由图10(c)可知,当颗粒阻尼吸振器的等效刚度系数k2增加时,轧机上工作辊的振幅逐渐减小,共振域也随之减小,共振峰也逐渐回偏;由图10(d)可知,当颗粒阻尼吸振器的等效阻尼系数c2增加时,共振峰及共振域都迅速减小。因此,在实际轧制过程中应尽量避免产生过大的轧制力,设计颗粒阻尼吸振器时,应在合理范围内选择较大的等效刚度系数k2及等效阻尼系数c2,从而降低主共振的振动幅值。
3 带有颗粒阻尼吸振器的轧机上工作辊内共振特性分析
3.1 系统内共振响应求解
考虑到带有颗粒阻尼吸振器的轧机上工作辊系统的内共振情况,假设
ω=ω10+εσ,ω20=ω10+εσ1,
ω30=ω20+εσ2=ω10+ε(σ1+σ2),
ω40=ω20+εσ3=ω10+ε(σ1+σ3)
式中:σ为轧机上工作辊的频率调谐因子;σ1,σ2,σ3为多自由度颗粒阻尼吸振器各个部分的频率调谐因子。代入式(9),为避免出现永年项,要求函数A1,A2,A3,A4满足
(16)
将复函数A1,A2,A3,A4写为指数形式
A1=0.5aeiφ1,A2=0.5beiφ2,
A3=0.5ceiφ3,A4=0.5deiφ4
式中,a,b,c,d,φ1,φ2,φ3,φ4为时间T1的函数,令
θ=σT1-φ1,θ1=σ1T1+φ2-φ1,
θ2=σ2T1+φ3-φ2,θ3=σ3T1+φ4-φ2
将A1,A2,A3,A4,θ,θ1,θ2,θ3代入式(16),令等式两边的虚部和实部相等,得
(17)
考虑静定轧机上工作辊处于稳态周期运动时

(18)
式(19)中,量的表达式见附录A。
3.2 带有吸振器的轧机上工作辊内共振响应分析
内共振过程是系统各运动部分之间的能量交换过程,根据系统的内共振幅频响应方程,仿真分析了颗粒阻尼吸振器各个参数对系统内共振的影响曲线。之后所有图中曲线a,b,c,d分别代表等效质量m1的量纲幅值、等效质量mc的量纲幅值、等效质量m3的量纲幅值以及等效质量mb的量纲幅值。
图11给出了不同等效刚度k2对应的系统内共振幅频响应曲线。由图11可知,随着k2的增加,曲线a的峰值以及共振域减小,同时吸振器各部分对轧机上工作辊的振动响应加快,即能量耗散加快,有助于轧机上工作辊更快达到稳定状态。因此在设计颗粒阻尼吸振器时,应尽量选择较大的等效刚度系数k2。
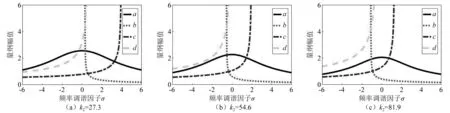
图11 等效刚度k2影响曲线Fig.11 Equivalent stiffness k2 influence curve
图12给出了不同等效阻尼系数c2对应的系统内共振幅频响应曲线。由图12可知,随着c2的增加,曲线a的峰值以及共振域减小,但是吸振器各部分对轧机上工作辊的振动响应逐渐滞后,考虑是阻尼c2增大使其本身耗能增加,当c2的能量耗散负荷达到饱和之后,吸振器的其他部分才成为耗能主体,所以随着c2增大会出现响应滞后现象。因此在设计颗粒阻尼吸振器时,要尽量选择较大的等效阻尼系数c2。

图12 等效阻尼c2影响曲线Fig.12 Equivalent damping c2 influence curve
图13给出了不同等效刚度系数k3对应的系统内共振幅频响应曲线。由图13可知,k3的增加对曲线c影响较大,对其余曲线影响不大,随着k3增加,质量外环m3对上工作辊的振动响应逐渐滞后,因此在设计颗粒阻尼吸振器时,要尽量选择较小的等效刚度系数k3。

图13 等效刚度k3影响曲线Fig.13 Equivalent stiffness k3 influence curve
图14给出了不同等效阻尼系数c3对应的系统内共振幅频响应曲线。由图14可知,c3的变化对曲线a,b,d影响不大。当c3较小时,质量外环m3对上工作辊的振动响应非常快,但是当曲线a达到峰值时,其响应迅速降低,之后吸振器中仅有颗粒部分有较大的耗能效果。随着c3的增加,m3又重新成为耗能主体,当c3继续增大时,m3响应加快。因此在设计颗粒阻尼吸振器时,应尽量选择较大的等效阻尼系数c3。
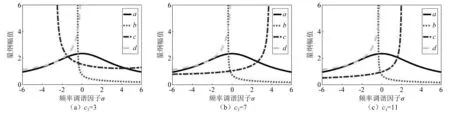
图14 等效阻尼c3影响曲线Fig.14 Equivalent damping c3 influence curve
图15为不同等效质量m2对应的系统内共振幅频响应曲线。由图15可知,m2的变化对系统的影响非常小。随着m2的增加,mc及mb对上工作辊的振动响应稍有加快。因此在设计颗粒阻尼吸振器时,可以在合理范围内选择较大的等效质量m2。

图15 颗粒容器质量m2影响曲线Fig.15 Particle container mass m2 influence curve
图16为不同外环质量m3对应的系统内共振幅频响应曲线。由图16可知,随着m3的增加,质量m3及mb在曲线a达到峰值前对上工作辊的振动响应逐渐增加,且当m3=2.55时,外环在曲线a的振动峰值前后都有很大响应,因此,在设计颗粒阻尼吸振器时,应尽量选择较大的外环质量m3。

图16 外环质量m3影响曲线Fig.16 Outer ring mass m3 influence curve
图17为不同颗粒群质量ma对应的系统内共振幅频响应曲线。由图17可知,随着ma的增加,曲线d对上工作辊的振动响应逐渐增加。因此较大的颗粒群质量对于耗散主振系统的能量是有利的。但是要考虑实际情况,颗粒群要有足够的空间来进行跳动,因此不能一味的增加颗粒的数量。
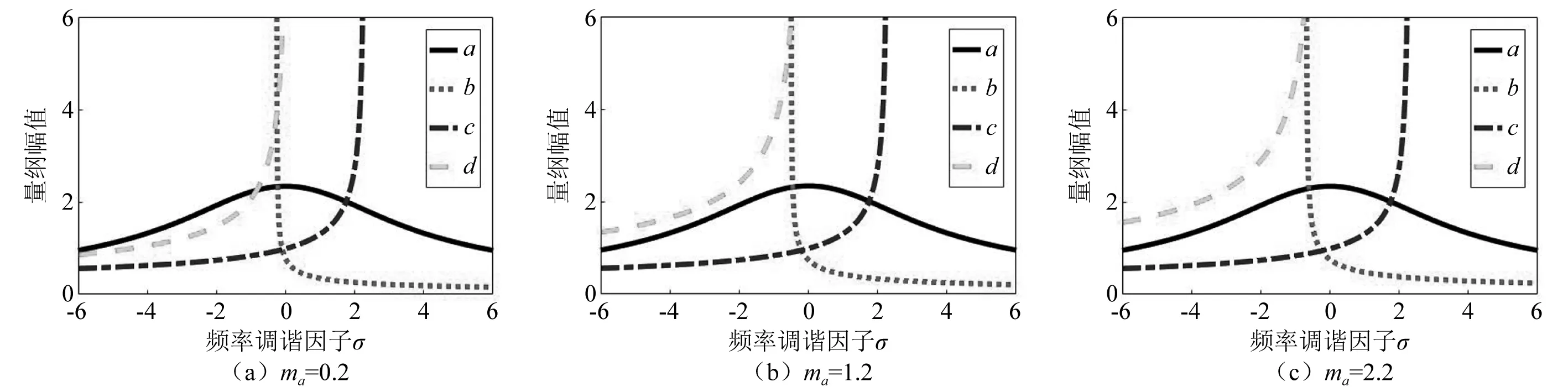
图17 颗粒质量ma影响曲线Fig.17 Particle quality ma influence curve
由于颗粒阻尼具有高度非线性的阻尼机理,当发生跳动的颗粒总质量mb增加时,其等效阻尼c与等效刚度k也会呈现实时非线性变化。即随着跳动颗粒数量的增加,颗粒间的碰撞与摩擦耗能必然增加,从而耗散主系统的振动能量,达到降低轧机上工作辊振幅的目的。
综合以上分析可以发现,上工作辊的振动能量最后主要是由等效质量mb以及m3来进行耗散的,即本文设计的颗粒阻尼吸振器中,颗粒群及质量外环是主要耗能部件。
4 颗粒阻尼吸振器的试验研究
4.1 试验装置
根据3.2节中分析的各参数对系统的影响,同时考虑振动控制目标结构、安装位置、安装空间等因素,加工颗粒阻尼吸振器如图18所示。

图18 颗粒阻尼吸振器Fig.18 Particle damping absorber
利用磁吸式三向加速度传感器、东华DH5922D动态信号测试分析系统、东华DHDAS软件平台、静定轧机、颗粒阻尼吸振器搭建试验平台,试验平台示意图如图19所示。
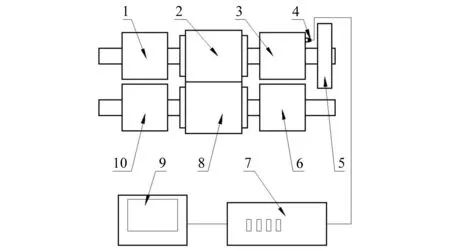
1.传动侧上轴承座;2.上工作辊;3.操作侧上轴承座;4.磁吸式三向加速度传感器;5.颗粒阻尼吸振器;6.操作侧下轴承座;7.东华DH5922D动态信号测试分析系统;8.下工作辊;9.东华DHDAS软件平台;10.传动侧下轴承座。图19 试验平台装置示意图Fig.19 Experimental platform device schematic diagram
4.2 试验结果及分析
为了与仿真结果相互验证,在每个颗粒容器中放500颗直径2 mm的铁珠进行试验。图20、图21分别为安装颗粒阻尼吸振器前后轧机上工作辊的时域曲线以及频谱曲线。

图20 安装吸振器前后系统时域曲线Fig.20 System time domain curve before and after installation of vibration absorber

图21 安装吸振器前后系统频谱曲线Fig.21 System spectrum curve before and after installation of vibration absorber
由图20可以看出,安装了吸振器之后,轧机上工作辊振幅降低25%左右,理论分析值为23%左右,结果基本吻合。存在的较小误差考虑是颗粒阻尼的耗能机理比较复杂,其实际耗能比理论分析值更多。由图21可以看出,上工作辊的振动信号主要由280 Hz左右的主共振频率以及75 Hz左右的谐振频率组成,与理论分析结果基本吻合。
综上所述,本文设计的颗粒阻尼吸振器能有效降低轧机上工作辊的振动幅值,并使振动系统更加稳定。
5 结 论
本文设计了一种应用于轧机上工作辊的多自由度颗粒阻尼吸振器,通过模拟仿真及试验研究了装有吸振器的轧机上工作辊的动力学行为,结论如下:
(1) 考虑了轧机轧制界面的非线性刚度,建立了安装颗粒阻尼吸振器的轧机上工作辊四自由度模型。采用多尺度法求解得到了系统主共振与内共振幅频响应方程,根据奇异性理论得到了系统的转迁集与相应临界点和各区域的分岔拓扑结构,控制开折参数落入区域Ⅰ和区域Ⅲ有助于提高系统的稳定性。
(2) 通过MATLAB仿真分析得到系统的时域曲线、相图以及频谱曲线,找到了振动系统主共振频率以及谐振频率。通过搭建试验平台,对颗粒阻尼吸振器的减振效果进行试验,结果与理论分析结果基本吻合。振幅抑制效果存在较小的误差,考虑是颗粒复杂的耗能机理所导致的。
(3) 综合主共振分析以及内共振分析,可以发现,本文设计的颗粒阻尼吸振器中质量外环及颗粒群是耗能主体部分。在设计颗粒阻尼吸振器时,应在合理范围内选择较大的等效刚度系数k2、较大的等效阻尼系数c2、较小的等效刚度系数k3、较大的等效阻尼系数c3、较大的等效质量m2、较大的外环质量m3以及较大的颗粒群质量ma。
由于颗粒阻尼具有强非线性特征,并且影响因素众多,因此,建立起一个更合理、更全面的等效理论模型以及对其耗能机理进行深入分析是下一步的工作重点。
附录A
式(18)中:
其中,
l=ac(ω30δ20γ40-ω10δ30γ30),
m=ac(δ20δ30+ω10ω30γ30γ40),
n=ad(ω40δ20γ50-ω10δ40γ30),
s=ad(δ20δ40+ω10ω40γ30γ50),
p=abω10ω20γ30(γ30+γ40+γ50),
q=2abω20δ20(σ-σ1),
w=2abω10ω20γ30(σ-σ1),
h=abδ20ω20(γ30+γ40+γ50),

