集群风场系统链式SVG高频谐振分析与抑制

陈继开，祝世启，王瑞全，李浩茹，边 竞，李国庆

集群风场系统链式SVG高频谐振分析与抑制

陈继开，祝世启，王瑞全，李浩茹，边 竞，李国庆

(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012)

针对含链式静止无功发生器(static var generator, SVG)的风场区域系统高频谐振问题，首先采用谐波线性化的方法建立包含锁相环、功率外环以及电流内环在内的SVG谐波阻抗模型。利用阻抗分析法对风场区域空载线路投入对SVG稳定性的影响进行分析，揭示风场区域系统高频谐振的发生机理。然后，为抑制系统高频谐振，提出一种基于电压前馈附加带阻滤波器的SVG高频谐振抑制策略。对SVG侧中高频段等效阻抗进行重塑，以保证在该频段系统呈正阻尼状态。并讨论带阻滤波器中心频率和阻尼系数对系统相位裕度的影响。最后利用搭建的含链式SVG风场区域系统仿真模型，验证了理论分析的正确性和所提抑制策略的有效性。

链式SVG；高频谐振；抑制策略；带阻滤波器；阻抗重塑

0 引言

近些年，风力发电作为技术最成熟、最具规模化开发潜力的可再生能源发电技术得到广泛运用[1-2]。截至2021年10月，我国风电装机容量约为3.0亿kW，同比增长30.4%，并提出到2030年风电、太阳能总装机容量达到12亿kW及以上[3]。伴随着风电的大规模开发，链式SVG因具有响应速度快、动态补偿能力强等优点被广泛应用于风场区域系统的无功补偿中[4-5]，但是随着SVG等无功补偿装置并网数量的增加，风场区域系统宽频带谐振问题也开始显现。有研究表明，风场区域系统易发生谐振频段为500～2000 Hz[6]，2013年广东某风场以及新疆某风场就分别出现了频率为650 Hz和1000 Hz的高频谐振现象[7]，而电力电子无功补偿装置的大量接入无疑进一步增加了集群风场区域系统高频谐振问题分析的难度。

目前，电力电子化电力系统的高频谐振问题已在柔性高压直流输电工程中有所显现，研究人员从工况切换条件下的换流站系统阻抗入手，对高频带系统的稳定性和失稳条件进行了探索。文献[8]以鲁西背靠背直流工程为例，建立了MMC-HVDC系统内换流站的精确模型，并结合阻抗稳定性理论从有源谐振和无源谐振两个层面揭示柔性直流系统高频谐振的发生机理。文献[9-11]基于谐波线性化的方法建立了MMC交直流侧系统等效模型，并通过附加有源阻尼、控制器参数优化以及电压前馈串联滤波器等方法，实现对系统高频谐振的抑制。由于MMC换流站和SVG功率电路均采用模块化级联拓扑，所以上述文献的研究方法对分析风场区域系统高频谐振问题也具有借鉴意义。对于风场区域系统高频谐振问题，业内研究重点主要集中在风场风机与电网间高频带等效阻抗关系的分析，从风机和电网整体系统鲁棒性的角度解释系统高频谐振发生原因。文献[12]以直驱风电系统为研究对象，建立了基于风机变流器控制的阻抗模型，利用阻抗分析法分析系统高频谐振的发生机理。在此基础上，文献[13]提出了基于DFIG的风力发电机综合阻抗模型，分析了网络拓扑、控制器参数以及镜像频率耦合对系统高频谐振的影响。文献[14]针对双馈风场与电压源型高压直流输电系统(VSC-HVDC)的高频稳定性问题，揭示了基于无锁相环直接功率控制的双馈风电互联系统高频谐振发生机理，并提出一种基于延时消除的高频谐振抑制策略。文献[15]分析了双馈风机输出功率、转子速度以及输电线路长度等对双馈风场区域系统谐波稳定性的影响，指出长输电线路的对地电容是影响系统高频谐振的主要因素。文献[16]充分考虑机侧变流器和网侧变流器的影响，建立不同补偿方式下双馈风电系统阻抗模型，揭示双馈风场高频谐振发生机理，并提出了附加阻尼的高频谐振抑制策略。

通过对现有文献分析可知，风场区域系统高频谐振的研究目前主要还是围绕风机变流器本体控制变化(或电网阻抗)导致的高频带系统稳定性下降问题进行分析，并没有考虑集群风场汇流站中大容量链式SVG在系统高频谐振中的作用。鉴于上述问题，本文以含链式SVG风场区域系统为研究对象，分析空载线路投入后SVG发生高频谐振的根本原因，首先建立包含锁相环、功率外环以及电流内环的正负序谐波阻抗模型，通过阻抗分析解释风场区域系统高频谐振的发生机理，并进一步讨论电流内环和功率外环参数对含链式SVG风场区域系统谐波稳定性的影响，继而提出一种基于电压前馈附加带阻滤波器的高频谐振抑制策略，最后通过仿真验证理论分析的正确性和所提抑制策略的有效性。

1 含链式SVG风场区域系统

1.1 风场区域系统结构与谐振问题

我国北部风电风场分布较为集中，距离较近的多个风电场通过220 kV(或110 kV)馈线集中接入汇流站，经汇流站升压后将电能送入输电网。某集群风场系统结构如图1所示，在风场汇流站内35 kV低压侧配置H桥级联的链式SVG，并通过35 kV/66 kV两绕组变压器与三绕组升压变压器相连，用以满足风场区域系统的无功需求。经过长期的现场运行监控发现，集群风场区域存在宽频带系统谐振问题。文献[17]以永磁同步型风场为研究背景，分析了变流器控制器参数、负载条件以及电网强弱与风场并网系统高频谐振的关系，指出风机网侧变流器电流内环控制与高频带宽锁相环相互作用是引发系统高频谐振的重要原因。文献[18]针对弱电网下双馈型风场高频谐振现象进行研究，利用阻抗分析方法研究了双馈风机与VSC-HVDC组成的复杂系统高频谐振发生机理，指出VSC控制延时是导致高频谐振出现的重要诱因，证明并网变流器控制延时与风场区域系统高频谐振存在密切关联。文献[19]研究了集群风场汇流站内静止无功发生器(SVG)机间交互对集群风场稳定性的影响，指出机间高频谐波环流不但可能导致SVG链内子模块直流电压失衡，当谐波超标触发高频分量保护装置动作切除一台SVG时，另一台SVG输出的高次谐波还可能污染区域电网，继而引发系统高频谐振。基于上述发现，围绕集群风场并网变流器高频谐振问题，本文以汇流站内并网链式SVG为研究对象，对风场区域空载线路投入导致系统内变流器高频谐振发生的机理和抑制方法展开研究。

图1 集群风场系统结构图

1.2 链式SVG控制原理

图2 链式SVG控制框图

2 基于谐波线性化的风场区域系统阻抗建模

针对风场区域系统在投入空载线路过程中出现的高频谐振现象，建立SVG侧等效阻抗模型。考虑到变流器直流侧电容电压对系统高频谐振特性影响较小[20]，为简化分析过程，在变流器阻抗建模时忽略直流侧电压总体控和相内控环节，主要考虑锁相环、功率外环以及电流内环控等环节。由于锁相环和Park变换环节将非线性因素引入到控制系统中，导致无法通过频域变换直接得到控制系统的线性模型，鉴于谐波线性化的方法克服了传统相量模型在频域范围上的局限性以及电磁暂态模型不可线性化的问题，并且由该方法获得的正负序阻抗具有明确的物理意义，故本文采用谐波线性化的方法对控制系统进行建模。假设并网点存在正、负序电压扰动，此时并网点以及SVG输出电流的A相时域表达式为

对式(1)、式(2)进行傅里叶变换，可以得到其频域表达式为

2.1 锁相环建模

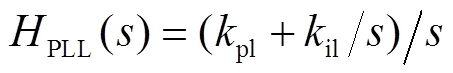
图3 同步参考坐标系锁相环控制框图

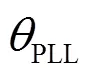
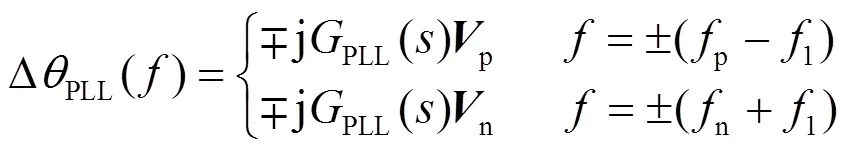
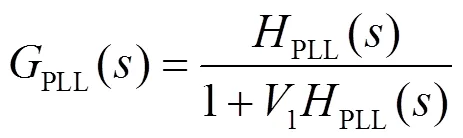
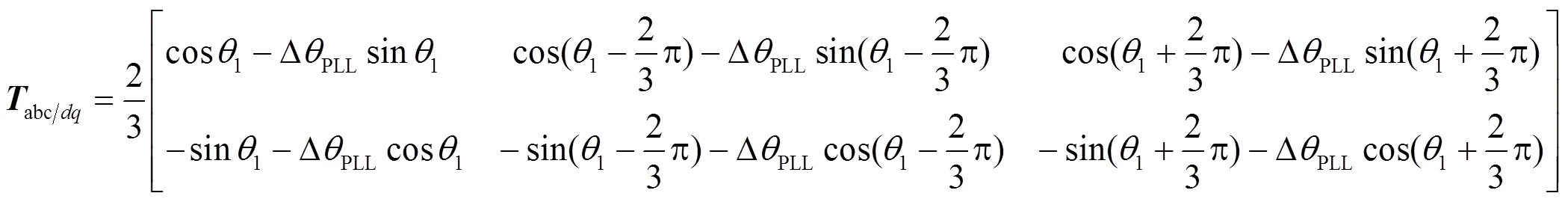
通过坐标变换可以得到链式SVG输出电流轴和轴分量的频域表达式为

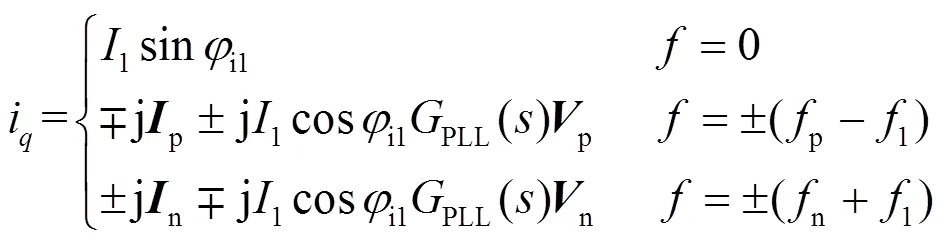
2.2 功率外环建模

集群风场汇流站链式SVG多采用定功率因数控制模式，功率外环需根据并网点有功功率和设定的功率因数来计算SVG无功补偿参考值，功率外环控制结构如图4所示。

图4 功率外环控制框图

由图4可以得到链式SVG指令电流表示为

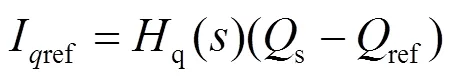
定义网侧电流的A相时域表示为

根据SVG补偿瞬时无功功率理论可知：

将并网点电压以及网侧电流的时域表达式代入式(12)并进行傅里叶变换，可以得到无功功率在频域下的表达式为

由式(10)和式(13)可以得到链式SVG指令电流的频域表达式为

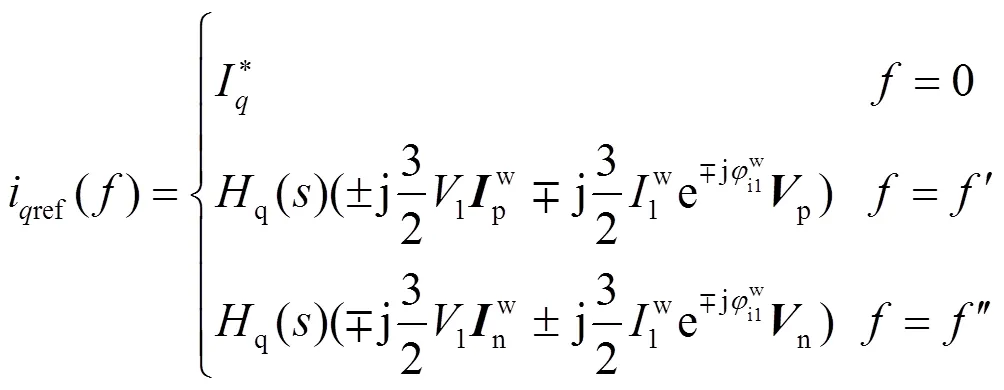
2.3 电流内环建模

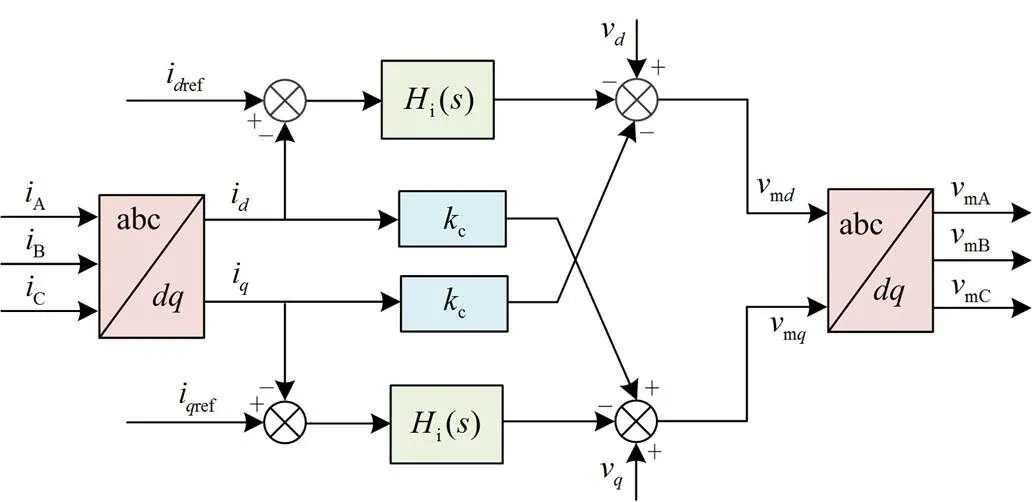
图5 链式SVG电流内环的控制框图

由图5得到电流内环的输出表达式为

对式(16)进行反park变换可以得到链式SVG三相调制波的时域表达式，如式(17)所示。

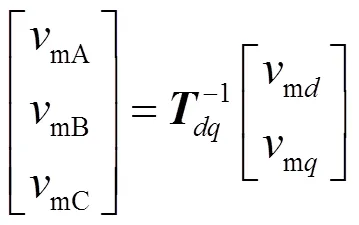
根据频域卷积定理，由式(16)和式(17)可得到链式SVG调制波的频域表达式，以A相为例：

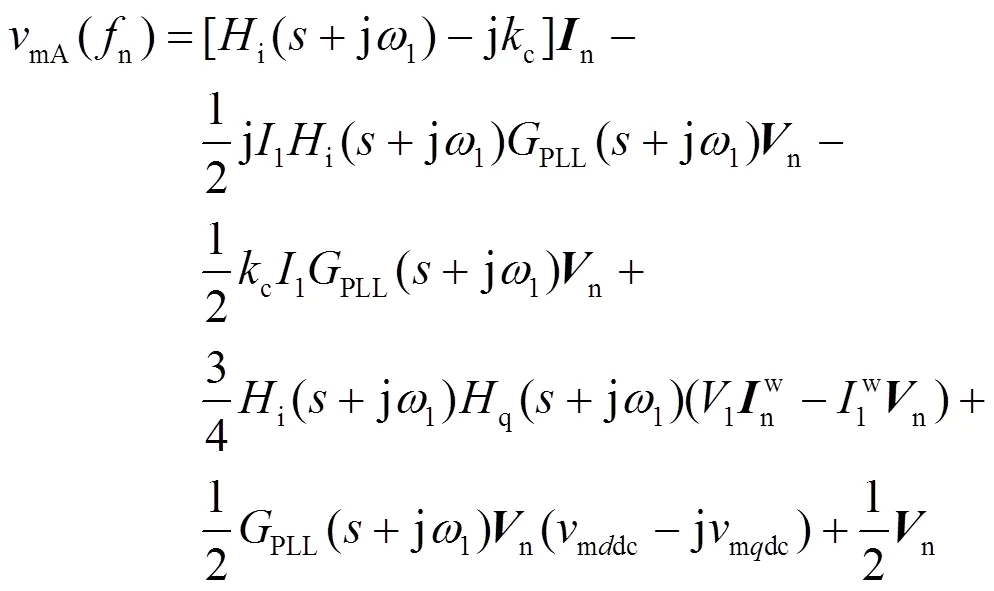
由于风电机组等效阻抗在中高频段主要表现为正阻感性[16]，为了简化分析过程，本文将集群风场等效为阻感性负载，最后根据小信号电压扰动与输出响应电流的关系可以得到SVG 侧正、负序谐波阻抗，如式(21)、式(22)所示。

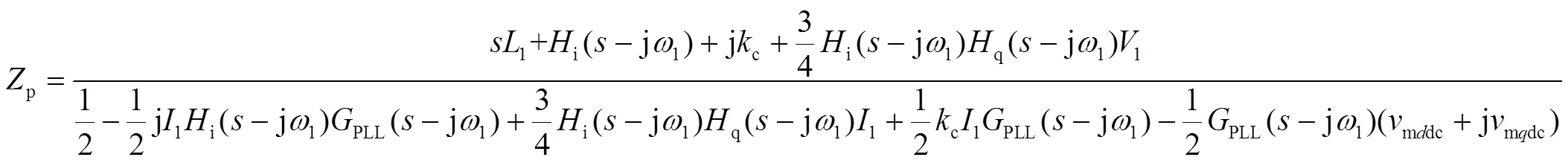
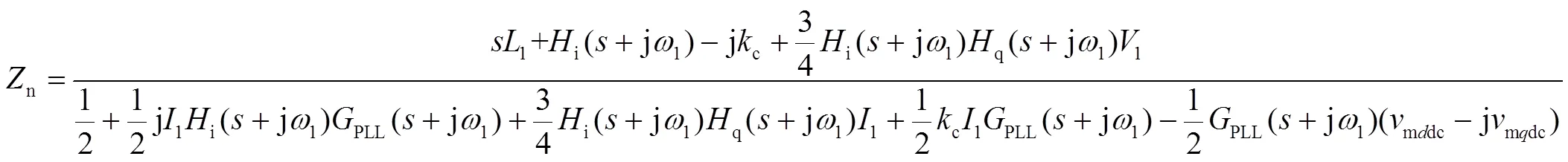
根据式(21)可以得到SVG侧正序阻抗的理论值，为了验证阻抗模型的正确性，本文通过频率扫描法对仿真系统阻抗进行测量，SVG侧正序阻抗的理论值与测量值对比如图6所示。观察图6可知，阻抗模型理论曲线与测量值基本吻合，验证了本文阻抗建模的正确性。

3 风场区域系统高频谐振机理分析及抑制

3.1 风场区域系统高频谐振机理分析

图6 SVG侧等效阻抗理论值与测量值对比

图7 风场区域系统等值电路图

图8 风场区域系统阻抗特性图

由式(21)和式(23)可知，电流内环以及功率外环PI控制器参数会对SVG侧的阻抗特性产生影响，但是在中高频段，PI控制器的积分项很小，因此可忽略PI控制器中积分项的影响。针对电流内环和功率外环比例系数对SVG侧阻抗特性的影响进行分析，阻抗特性曲线如图9所示。由图9(a)可知，随着电流内环比例系数的增加，系统的谐振峰值增大，频率向高频偏移，但是SVG侧等效阻抗与电网侧等效阻抗幅值交点处的相位差始终大于180º，系统仍处于不稳定状态。由图9(b)可知，随着功率外环比例系数的增加，系统的谐振峰值增大，频率向高频偏移，SVG侧等效阻抗的负阻尼区减少，系统的相位裕度得到小幅提升，相较于电流内环比例系数而言，功率外环比例系数对SVG侧阻抗特性的影响较大，但是幅值交点处的相位裕度仍小于零，系统处于不稳定状态。

通过上述分析可知，SVG侧等效阻抗出现负阻尼是系统发生高频谐振的必要条件，SVG侧等效阻抗与电网侧等效阻抗幅值交点处的频率即为系统的谐振频率，在系统稳定运行的前提下，通过优化系统控制器参数可以在一定程度上改善SVG侧阻抗特性，但无法保证对系统高频谐振的抑制效果，故要从减少SVG侧等效阻抗的负阻尼区间和增加风场区域系统相位裕度两方面入手，构建一种新的风场区域系统高频谐振抑制策略。

图9 控制器参数对SVG侧阻抗特性的影响

3.2 风场区域系统高频谐振抑制策略

由上节分析可知，系统发生高频谐振的必要条件是SVG侧等效阻抗出现负阻尼，文献[16]指出在控制环中附加滤波器可以阻断谐波的传递路径，重塑系统等效阻抗。针对风场区域系统中的高频谐振问题，本文提出了一种基于电压前馈附加带阻滤波器的高频谐振抑制策略，对SVG侧等效阻抗进行重塑，进而抑制系统可能出现的高频谐振，提高系统的谐波稳定性。电压前馈附加带阻滤波器控制框图如图10所示。

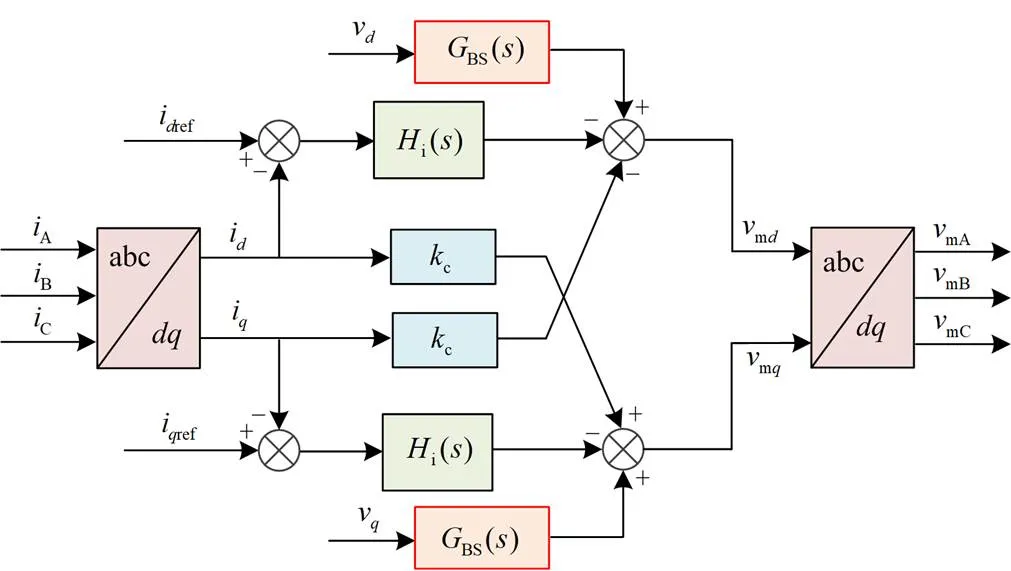
图10 电压前馈附加带阻滤波器控制框图

在电压前馈中引入带阻滤波器后，式(21)可以改写为

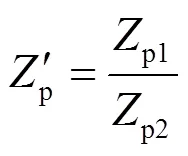
其中：

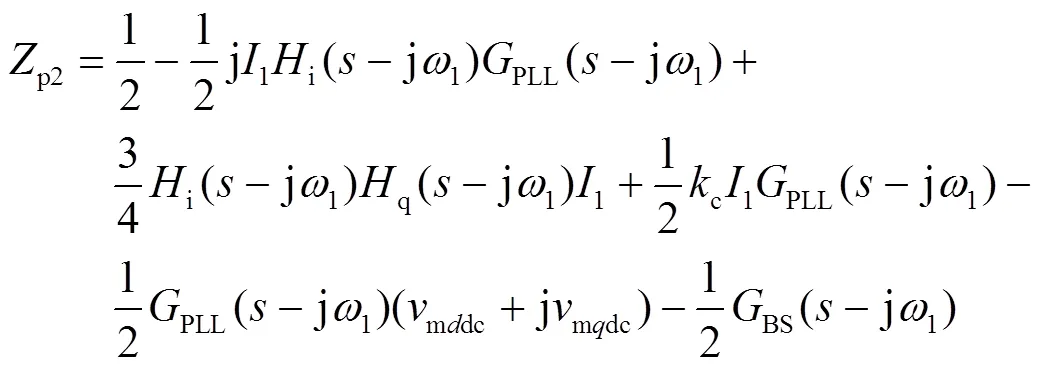
图11 带阻滤波器对风场区域系统阻抗特性的影响

对比图8和图12可以发现，电压前馈中附加带阻滤波器后，SVG侧等效阻抗的低频特性未受其影响，由于电压前馈中串联带阻滤波器增加了系统的阻尼，SVG侧等效阻抗与电网侧等效阻抗的幅值交点向右偏移，由原先的1535 Hz变为1690 Hz，SVG侧等效阻抗的负阻尼频段由原先的470～1615 Hz减小为956～1158 Hz，大大降低了系统发生高频谐振的可能性，实现了对SVG侧中高频段阻抗的重塑。SVG侧等效阻抗与电网等效阻抗幅值交点处的相位裕度由原先的-9.5º增加到40.8º，相位裕度大于30º，满足系统稳定性的要求，具有较强的抗谐波干扰能力，可以有效抑制风场区域系统的高频谐振。

图12 阻抗重塑后风场区域系统阻抗特性图

4 仿真验证及分析

为验证风场区域系统高频谐振机理分析的正确性以及所提高频谐振抑制策略的有效性，本文基于RTLAB5600仿真平台搭建了含链式SVG的风场区域系统仿真模型，SVG参数如表1所示。

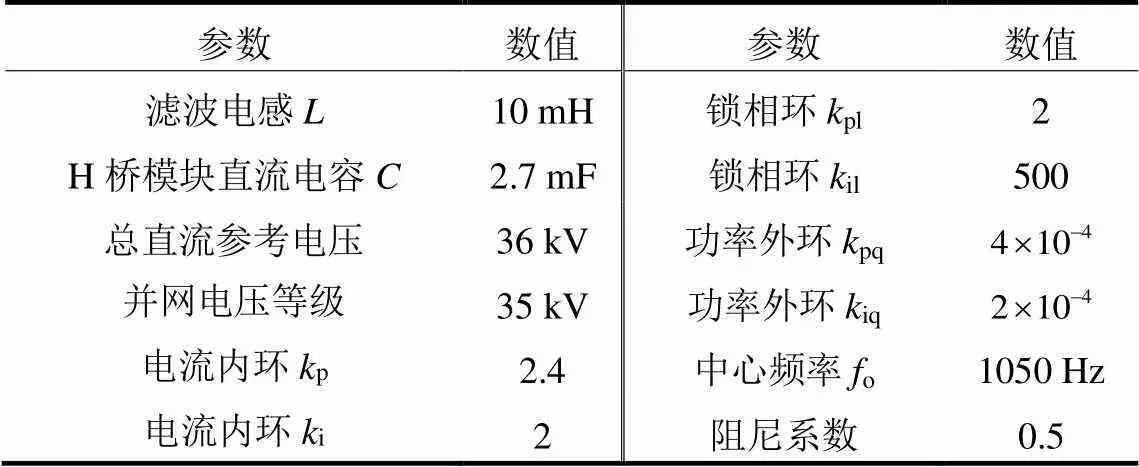
表1 链式SVG参数

风场区域系统最初稳定运行，1 s时投入空载线路，1.2 s引入高频谐振抑制策略对SVG侧高频等效阻抗进行重塑，并网点电压的整体仿真波形如图13所示。由图13可知，在1 s投入空载线路后，风场区域系统由于相位裕度不足而发生高频谐振，在1.2 s引入本文提出的高频谐振抑制策略，系统高频谐振得到了有效抑制，SVG恢复正常运行。

图13 并网点电压波形图

图14 投入空载线路前后仿真图

引入高频谐振抑制策略前后系统仿真波形以及傅里叶分析结果如图15所示。对比图14和图15可知，引入高频谐振抑制策略后系统交互频率向高频方向偏移，由原来的1550 Hz 和1650 Hz变为1750 Hz和1850 Hz，与3.1节理论分析基本一致；并网点电压的THD由62.16%减少为0.76%，网侧电流THD由原先的49.92%减少为1.65%，SVG输出电流的THD由原先的121.54%减少为4.54%，谐振现象消失，系统高频谐振得到有效抑制。

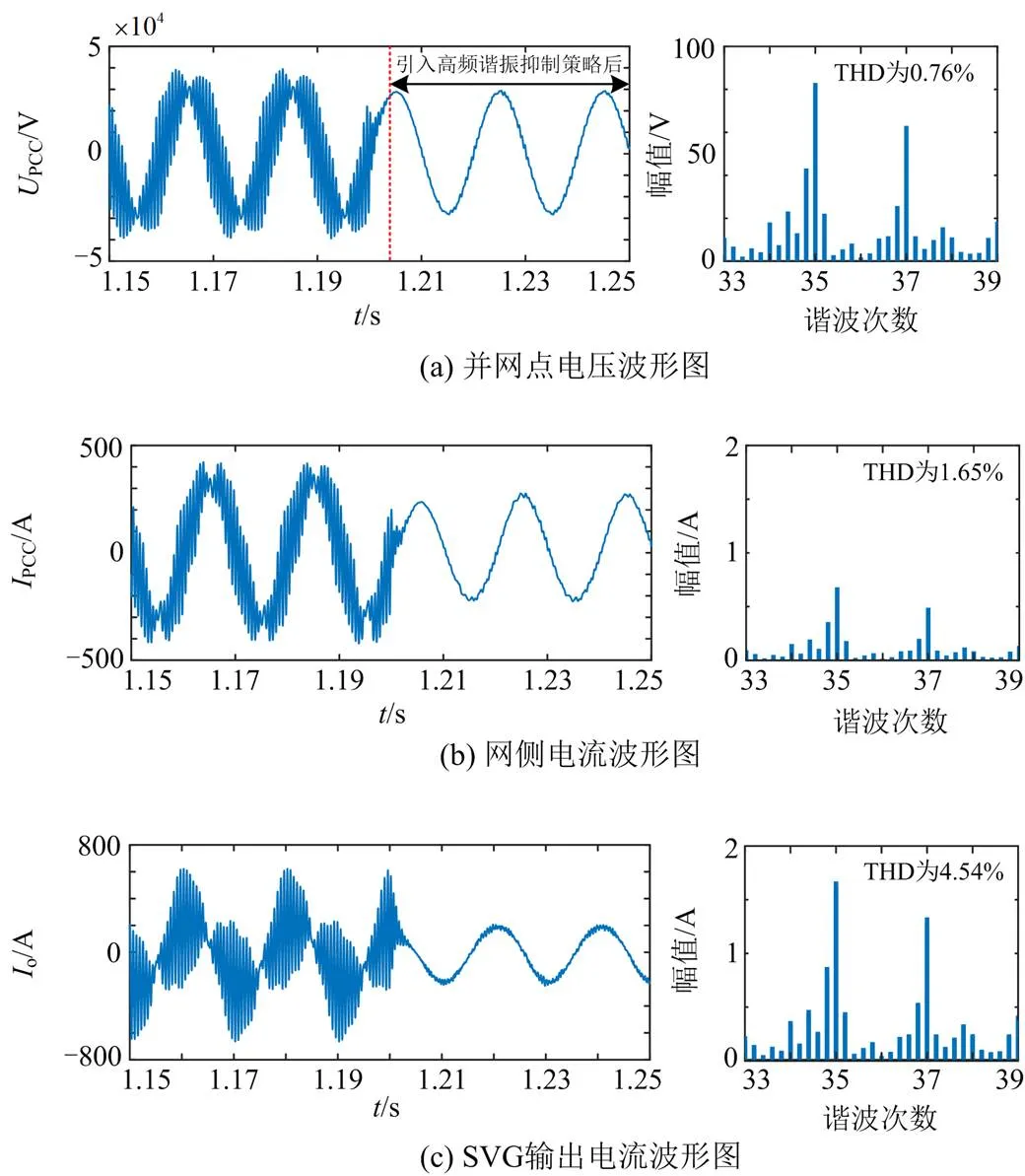
图15 引入高频谐振抑制策略前后仿真图

5 结论

本文基于阻抗分析理论分析了风场区域系统高频谐振发生机理，归纳出导致风场区域系统发生高频谐振的根本原因，并提出一种基于电压前馈附加带阻滤波器的高频谐振抑制策略，通过理论分析和仿真验证得到以下结论：

1) 含有链式SVG的风场区域系统在低频段相位裕度较大，但空载线路投入将导致其在中高频段存在相位裕度小于零的情况，呈现负阻尼特性，增加了风场区域系统发生高频谐振的风险。

2) 在保证系统稳定运行的前提下，优化链式SVG控制器参数对SVG侧阻抗特性的改善效果有限，仅依靠优化链式SVG控制器参数无法从根本上消除系统高频谐振。

3) 本文所提的基于电压前馈附加带阻滤波器的高频谐振抑制策略能够对风场区域系统中高频段阻抗进行重塑，提高系统的相位裕度，减少SVG侧等效阻抗的负阻尼区间，有效抑制系统高频谐振的发生，其调节范围和抑制效果由中心频率和阻尼系数共同决定。

[1] 郑黎明, 贾科, 毕天姝, 等. 海上风电接入柔直系统交流侧故障特征及对保护的影响分析[J]. 电力系统保护与控制, 2021, 49(20): 20-32.

ZHENG Liming, JIA Ke, BI Tianshu, et al. AC-side fault analysis of a VSC-HVDC transmission system connected to offshore wind farms and the impact on protection[J]. Power System Protection and Control, 2021, 49(20): 20-32.

[2] TUMMALA A S L V. A robust composite wide area control of a DFIG wind energy system for damping inter-area oscillations[J]. Protection and Control of Modern Power Systems, 2020, 5(3): 260-269.

[3] 文劲宇, 周博, 魏利屾. 中国未来电力系统储电网初探[J]. 电力系统保护与控制, 2022, 50(7): 1-10.

WEN Jinyu, ZHOU Bo, WEI Lishen. Preliminary study on an energy storage grid for future power system in China[J]. Power System Protection and Control, 2022, 50(7): 1-10.

[4] 刘伟. 电网严重故障下的电压稳定应对措施分析[J]. 电力系统保护与控制, 2020, 48(16): 163-170.

LIU Wei. Analysis of voltage stability countermeasures under a severe fault in a power grid[J]. Power System Protection and Control, 2020, 48(16): 163-170.

[5] 陈继开, 王鹏, 徐永海, 等. SVG机间谐波交互对子模块直流电压的影响分析与抑制方法[J]. 电网技术, 2020, 44(2): 637-645.

CHEN Jikai, WANG Peng, XU Yonghai, et al. Analysis of influence of harmonic interaction between SVGs on sub-module DC voltage and suppression method[J]. Power System Technology, 2020, 44(2): 637-645.

[6] EBRAHIMZADEH E, BLAABJERG F, WANG X, et al. Harmonic stability and resonance analysis in large PMSG-based wind power plants[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 12-23.

[7] 秦世耀, 李少林, 王瑞明, 等. 大容量永磁同步风电机组系统谐振与抑制策略[J]. 电力系统自动化, 2014, 38(22): 11-16.

QIN Shiyao, LI Shaolin, WANG Ruiming, et al. Resonance and suppression strategy of large-capacitypermanentmagnetsynchronous generator wind turbine system[J]. Automation of Electric Power Systems, 2014, 38(22): 11-16.

[8] 代锋, 王钢, 曾德辉, 等. MMC-HVDC输电系统中高频阻抗建模及谐振机理分析[J/OL]. 电网技术: 1-18 [2021-12-24]. DOI:10.13335/j.1000-3673.pst.2021.1124.

DAI Feng, WANG Gang, ZENG Zhihui, et al. Medium- and high-frequency impedance modeling and resonance mechanism analysis of MMC-HVDC transmission system[J/OL]. Power System Technology: 1-18[2021-12- 24]. DOI: 10.13335/j.1000-3673.pst.2021.1124.

[9] 陈威, 汪娟娟, 叶运铭, 等. 柔性直流输电系统交流侧中高频谐振附加阻尼抑制措施[J]. 电力系统自动化, 2021, 45(18): 151-161.

CHEN Wei, WANG Juanjuan, YE Yunming, et al. Additional damping suppression measures for medium- and high-frequency resonance on AC side of MMC- HVDC transmission system[J]. Automation of Electric Power Systems, 2021, 45(18): 151-161.

[10] 郭贤珊, 刘泽洪, 李云丰, 等. 柔性直流输电系统高频振荡特性分析及抑制策略研究[J]. 中国电机工程学报, 2020, 40(1): 19-29, 370.

GUO Xianshan, LIU Hongze, LI Yunfeng, et al. Characteristic analysis of high-frequency resonance of flexible high voltage direct current and research on its damping control strategy[J]. Proceedings of the CSEE, 2020, 40(1): 19-29, 370.

[11] SUN Jian, LIU Hanchao. Sequence impedance modeling of modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in power Electronics, 2017, 5(4): 1427-1443.

[12] EBRAHIMZADEH E, BLAABJERG F, WANG X, et al. Reducing harmonic instability and resonance problems in PMSG-based wind farms[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 77-83.

[13] ZHANG Yonggang, KLABUNDE C, WOLTER M. Frequency-coupled impedance modeling and resonance analysis of DFIG-based offshore wind farm with HVDC connection[J]. IEEE Access, 2020, 8: 147880-147894.

[14] 年珩, 童豪, 胡彬, 等. 无锁相环直接功率控制下双馈风电与VSC-HVDC互联系统高频振荡抑制技术[J]. 电网技术, 2020, 44(2): 637-645.

NIAN Heng, TONG Hao, HU Bin, et al. High frequency resonance suppression of doubly fed induction generator based on direct power control without phase-locked loopconnected to VSC-HVDC system[J]. Power System Technology, 2020, 44(2): 637-645.

[15] SONG Y, EBRAHIMZADEH E, BLAABJERG F. Analysis of high-frequency resonance in DFIG-based offshore wind farm via long transmission cable[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1036-1046.

[16] 刘其辉, 董楚然, 于一鸣. 双馈风电并网系统高频谐振机理及抑制策略[J]. 电力自动化设备, 2020, 40(9): 163-172.

LIU Qihui, DONG Churan, YU Yiming. High frequency resonance mechanism and suppression strategy of doubly-fed wind power grid-connected system[J]. Electric Power Automation Equipment, 2020, 40(9): 163-172.

[17] DU Wenjuan, WANG Yijun, WANG Yang, et al. Analytical examination of oscillatory stability of a grid-connected PMSG wind farm based on the block diagram model[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5683-5670.

[18] PANG Bo, NIAN Heng, XU Yunyang. Mechanism analysis and damping method for high frequency resonance between VSC-HVDC and the wind farm[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 984-994.

[19] CHEN Jikai, HU Yang, WANG Yongquan, et al. Study on harmonic interaction between paralleled STATCOMs with cascaded H-bridge topology in wind farm clusters[J]. IET Renewable Power Generation, 2021, 15(11): 2515-2525.

[20] 李云丰, 贺之渊, 孔明, 等. 柔性直流输电系统高频稳定性分析及抑制策略(二): 阻尼控制抑制策略[J]. 中国电机工程学报, 2021, 41(19): 6601-6616.

LI Yunfeng, HE Zhiyuan, KONG Ming, et al. High frequency stability analysis and suppression strategy of MMC-HVDC systems (part II): damping control suppression strategy[J]. Proceedings of the CSEE, 2021, 41(19): 6601-6616.

[21] 刘人志, 陈卓, 唐文博, 等. 弱电网下计及锁相环影响的 LCL 型并网逆变器控制策略[J]. 电力系统保护与控制, 2022, 50(5): 178-187.

LIU Renzhi, CHEN Zhuo, TANG Wenbo, et al. Control strategy of an LCL type grid-connected inverter with the influence of a phase-locked loop under a weak power grid[J]. Power System Protection and Control, 2022, 50(5): 178-187.

[22] MAN Jiufang, XIE Xiaorong, XU Shukai, et al. Frequency-coupling impedance model based analysis of a high-frequency resonance incident in an actual MMC-HVDC system[J]. IEEE Transactions on Power Delivery, 2020, 35(20): 2963-2971.

[23] AMIN M, MOLINAS M. Small-signal stability assessment of power electronics based power systems: a discussion of impedance- and eigenvalue-based methods[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 5014-5030.

[24] RYGG A, MOLINAS M, ZHANG C, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1391.

Analysis and suppression of chained SVG high-frequency resonance in a cluster wind farm system

CHEN Jikai, ZHU Shiqi, WANG Ruiquan, LI Haoru, BIAN Jing, LI Guoqing

(Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology (Northeast Electric Power University), Ministry of Education, Jilin 132012, China)

To solve the high frequency resonance problem of a wind field regional system with a chained static var generator (SVG), an SVG harmonic impedance model including phase-locked, power outer and current inner loops is first established by the harmonic linearization method.An impedance analysis method is applied to the unloaded line in the wind field area to analyze the effect on the stability of the SVG. This reveals a high frequency resonance mechanism of the wind field regional system. Then, to suppress the high frequency resonance of the system, an SVG-BASED high frequency resonance suppression strategy based on additional band stop filter is proposed in the voltage feedforward compensator. The equivalent impedance of the SVG side in the middle and high frequency band is reconstructed to ensure that the positive damping state of the system is in the band. The influence of the center frequency and damping coefficient of the band stop filter on the phase margin of the system is discussed.Finally, a simulation model of the wind field area system containing chained SVG is used to verify the correctness of the theoretical analysis and the effectiveness of the proposed suppression strategy.

chained staticvar generator; high frequency resonance; suppression strategy; band stop filter; impedance remodeling

10.19783/j.cnki.pspc.220273

国家自然科学基金面上项目资助(52077030)

This work is supported by the National Natural Science Foundation of China (No. 52077030).

2022-03-04；

2022-06-09

陈继开(1977—)，男，博士，教授，研究方向为电能质量分析与控制、柔性直流输电技术等；E-mail: chenjikai1977@163.com

李浩茹(1978—)，女，通信作者，硕士，讲师，研究方向为电能质量分析与控制。E-mail: lihaoru@neepu.edu.cn

(编辑 魏小丽)