含可控光伏的主动配电网多时间尺度鲁棒优化调度

茹秋实，米雪峰，宋志刚，刘金涛，雷霞

(1.国网甘肃省电力公司陇南供电公司，甘肃 陇南 742500；2. 西华大学 电气与电子信息学院，四川 成都 610039)

2021年9月14日，国家能源局正式印发《关于公布整县(市、区)屋顶分布式光伏开发试点名单的通知》，预示我国将大力提高分布式光伏(photovoltaic，PV)发电的渗透率，配电网系统的形态正发生根本变化[1-3]，主动配电网的架构搭建初具规模。并且对于低压配电网来说，线路中电抗与电阻值相差不大，随着配电网分布式电源及储能系统(energy storage system，ESS)等有功系统在配电网中的配置，配电网运行特点也逐步向有功、无功协调调度转变[4-8]。相较于配电网无功优化，配电网有功、无功协调优化调度的研究，主要体现在对配电网有功电源(例如分布式电源和ESS)的控制建模，以及对配电网中各类有功无功设备在多时间尺度上的联合调度建模[9-10]。

近年来，在配电网优化中考虑光储技术与无功设备在多时间尺度上协调调度已有相关研究：文献[11-13]实现了考虑PV逆变器可控性的配电网分布式优化；文献[14]则从PV系统的概率模型出发，建立起含可控PV的主动配电网优化调度模型；文献[15-16]将PV逆变器的可控性描述为逆变器的下垂控制特性，以此来解决配电网电压问题。然而这些研究对于PV逆变器可控性描述都仅限于文献[11]所提及的逆变器优化调度(optimal inverter dispatch，OID)模式，缺少对PV逆变器运行模式切换功能的建模分析。为此，文献[17]在配电网优化中计及了PV逆变器处于运行或者不运行状态之间进行切换。文献[18-19]则进一步考虑了PV逆变器的多种运行模式切换能力，并利用仿生算法进行配电网优化调度求解；然而并未对“源-荷”的不确定影响进行建模，导致整体优化模型仍然处于确定性优化模型。对于配电网多时间尺度优化调度来说，在日前调度阶段不考虑“源-荷”不确定性所带来的影响是纰谬的，因此文献[20]通过轮盘机制随机生成风电出力和太阳辐照的场景来表征新能源出力的不确定性，分析其产生的不良影响；但是随机产生的场景并不能满足鲁棒性要求。为了在数学规划法中体现不确定性，文献[21]提出了基于列和约束生成(column and constraint generation，C&CG)算法的两阶段鲁棒优化方法，以求得最坏场景下的最优化解。文献[22-23]提出PV逆变器可根据配电网需要进行调节，同时将2种不同控制模式的PV逆变器引入配电网优化中，并利用两阶段鲁棒优化方法对配电网模型进行求解；但是其模型中仅只有对来自荷不确定性的表述，没有实现PV波动出力与PV控制模式切换的耦合计算。文献[24-27]利用历史数据进行聚类得到负荷的不确定性场景，同时利用正态分布模拟PV出力误差，然后再通过场景缩减法来得到PV的不确定性场景；但是对大量的历史数据进行处理将会增大系统计算量，与此同时场景缩减法并不能满足配电网优化的鲁棒性需求。文献[28]从仿射运算的角度出发，通过不断添加新的噪声元模拟“源-荷”的不确定性；但是该类运算新添加的噪声元缺乏物理意义，难以表征“源-荷”的实际波动性，究其本质依旧类似于随机规划。更进一步地，配电网“源-荷”在短时间尺度上的波动性相较于长时间尺度更大，若配电网各类设备依旧按照长时间尺度优化调度结果投入运行，那么“源-荷”不确定性所造成的功率实时不平衡只能由电源点进行补偿，从而使线路上流动的有功、无功功率波动增大，这将不利于配电网安全稳定运行。上述研究绝大多数是在日前预测曲线所做出的优化策略[11-17,22-27]，在优化过程中既缺乏日内调节策略，又缺少对离散调节元件〔投切电容组(shunt capacitor，SC)和调节有载调压器(on-load tap changer，OLTC)〕与连续调节元件的调度分配分析[18]，所以基于日前预测曲线的优化策略往往难以满足配电网运行的要求；因此，在考虑“源-荷”不确定性的同时，实现一种既考虑配电网多时间尺度调度优化，又计及PV逆变器功能切换的配电网优化方法具有重要意义。

鉴于此，为了保证配电网系统的安全稳定运行，本研究基于二阶锥规划的配电网潮流模型、两阶段鲁棒优化和滚动优化理论建立含可控PV逆变器的主动配电网多时间尺度鲁棒优化调度模型。首先，利用大M法等方法对PV逆变器运行策略切换进行建模，将PV逆变器运行策略切换模型配置到两阶段鲁棒优化之中，以体现“源-荷”的不确定性对配电网带来的影响，构建协调“源-储-无功设备”配电网小时级调度模型；其次，将小时级调度所得到的SC、OLTC、ESS和静止无功补偿(static var compensation，SVC)等无功-电压控制(var-voltage control，VVC)设备的有功、无功功率调度量保留至分钟级调度中，建立分钟级优化调度模型，得到最优的PV逆变器模式切换策略及PV无功补偿量；最后，本文在改进的IEEE 33节点测试系统进行仿真计算，以验证本文模型及算法的有效性与合理性。

1 考虑PV逆变器控制模式的配电网优化调度模型

1.1 配电网的优化运行约束

本研究将不同运行模式下的PV出力作为不确定集，体现于辐射状配电网的Distflow支路潮流模型中，并建立配电网的优化运行约束模型。

1.1.1 功率平衡约束

针对辐射状配电网，通常用图1所示的Distflow支路潮流模型表示。

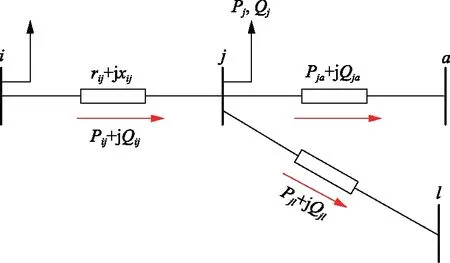
图1 Distflow潮流模型Fig.1 Distflow model

对于配电网中的节点j，有：

Ppv，out,j,t+Pdch,j,t-Pch,j,t；

(1)

Qpv，out,j,t+Qsc,j,t+Qsvc,j,t；

(2)

Vj,t=Vi,t-2(Pij,trij+Qij,txij)+

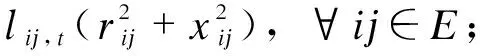
(3)

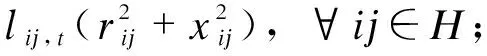
(4)

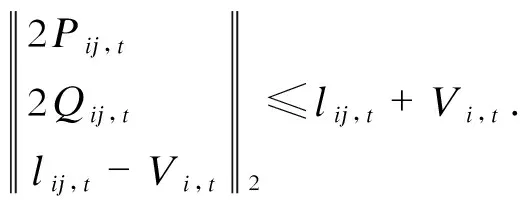
(5)

式(1)—(5)中：π(j)为以节点j为首节点的支路集合；lij,t、Pij,t、Qij,t分别为在时刻t支路ij流过的电流平方值、有功功率、无功功率，用下标t表示时刻t的参数，用下标ij表示支路ij的参数，下同；Pj,t、Qj,t分别为节点j在时刻t注入的有功、无功功率；Vj,t、Vi,t分别为节点j、i在时刻t的电压幅值平方值，用下标j、i表示节点j、i的参数，下同；r、x分别为支路的电阻、电抗；Ppv，out、Qpv，out分别为节点所连接的PV发出的有功、无功功率；Pch、Pdch分别为节点所连接的储能元件的充、放电功率；Qsc、Qsvc分别为节点所连接的无功补偿电容组、SVC的出力；E为没有安装OLTC的支路集合；H为安装OLTC的支路集合；Hij,t为支路ij上OLTC的变比。

1.1.2 节点电压约束

节点电压约束为

(6)

式中Ui为节点i的电压，用下标min、max表示参数的最小、最大值，下同。

1.1.3 支路电流约束

支路电流约束为

(7)

式中Iij,max为支路ij电流最大值。

1.1.4 并联电容组约束

并联电容器属于离散型的无功补偿设备。

Qsc,j,t=Ksc,j,tΔQsc，

(8)

Qsc,j,min≤Qsc,j,t≤Qsc,j,max.

(9)

式(8)、(9)中：Ksc为SC的组数；ΔQsc为单台电容器的无功补偿量。

并联电容组只能分组投切，所以式(8)是离散的优化模型，可以通过以下方法转化为0-1整型规划的模型[29]：

0≤Ksc,j,t=20δ0+21δ1+…+2bδb≤Ksc,j,max，

δ0,δ1,…,δb∈{0,1}.

(10)

式中：b根据SC具体安装组数进行确定；δ0,δ1,…,δb为二进制辅助变量。

为了延长SC的使用寿命，在1个周期内SC的投切次数是有一定限制的。

(11)

式中：ε1j(t)、ε2j(t)均为二进制变量，只有当Ksc,j,t+1-Ksc,j,t≠0时，ε1j(t)、ε2j(t)有且仅有1位数字为1，说明SC已动作；Nsc,max为SC的最大投切次数；T为调度周期内的时刻点数，1个调度周期被各时刻点分隔成4个时段，在小时级调度周期每个时段长为1 h，在分钟级调度周期每个时段长为15 min。

1.1.5 储能装置运行约束

储能装置运行约束为

(12)

0≤Pch,j,t≤Pch,j,maxDch,j,t.

(13)

0≤Pdch,j,t≤Pdch,j,maxDdch,j,t.

(14)

Dch,j,t+Ddch,j,t≤1.

(15)

Wj,max×20%≤Wj,t≤Wj,max.

(16)

式(12)—(16)中：W为节点所连接的ESS电量；ηch、ηdch分别为充、放电效率；式(12)表示为保证在新的调度周期内ESS具有相同的调节能力，每个调度周期的初始储能设置为相同；由于ESS的充放电不能同时进行，引入Dch、Ddch2个0-1变量以表示ESS在某时刻只能处于充电、放电和不充不放3种状态其中之一；式(16)表示ESS的电量约束，考虑储能装置的使用寿命，将其实际充放电范围设定为20%～100%。

1.1.6 SVC出力约束

SVC出力约束为

Qsvc,j,min≤Qsvc,j≤Qsvc,j,max.

(17)

1.1.7 OLTC约束

(18)

(19)

(20)

式(18)—(20)中：mij,g,t、hj,g,t均为转化中的辅助变量；M为任意大的实数；式(19)中的约束是2个互补条件，取令目标函数最优的条件。

在1个调度周期内，OLTC的档位调节次数会受到一定的限制，即

|mij,g,t+1-mij,g,t|)≤2NT,max.

(21)

式中NT,max为1个调度周期内变压器投切的最大次数。

1.2 PV逆变器运行模式切换模型

文献[24]中提出PV逆变器可根据电网需要来提供辅助服务以提高配电网的安全性，因此在配电网运行时需要对PV逆变器的运行模式进行切换[21]。PV逆变器的4种控制模式如图2所示，分别为：模式a，不采用辅助模式；模式b，无功功率控制(reactive power control，RPC)模式；模式c，有功功率限制(active power curtailment，APC)模式；模式d，OID模式。由于模式c不具有无功调节能力，所以本文主要讨论PV逆变器的模式a与模式b之间(a-b)和模式a与模式d之间(a-d)切换能力。图2中PPV为该环境下PV的最大有功出力，SG为PV逆变器的视在功率，QPV为PV无功出力上限。

图2 PV逆变器的4种控制模式Fig.2 Four control modes of PV inverter

4种控制模式中，Ppv，out、Qpv，out具体表达如式(22)—(25)所示：

(22)

(23)

(24)

(25)

以上模型仅为PV逆变器的各种运行模式，可通过如下变换实现各运行模式之间的转化：

a)a-b转化模型：

Ppv,out=PPV，

(26)

(27)

-Qpv,out,maxzg≤Qpv,out≤Qpv,out,minzg.

(28)

式(28)中zg为PV逆变器a-b模式切换变量。

Qpv，out，maxzg是连续变量和二进制变量所构成的非凸双线性项，于是可以用大M法重新表述式(28)，即

(29)

b)a-d转化模型：

PPV(1-zf)≤Ppv,out≤PPV，

(30)

(31)

-Ppv,outzf≤Qpv,out≤Ppv,outzf.

(32)

式(30)中zf为PV逆变器a-d模式切换变量。为使Ppv，outzf也可以用大M法重新表述，需先引入替换变量Gpv，out来代替Ppv，outzf，再进行式(33)—(35)变换。

(33)

-Gpv,out≤Qpv,out≤Gpv,out，

(34)

(35)

安装到某一节点的PV逆变器可以自主选择控制模式，其有功无功调节能力在模式a与模式d或模式a与模式b之间切换。对于具有a-b切换能力的逆变器来说，zg=0时表示逆变器选择模式a运行，zg=1表示逆变器选择模式b运行；对于具有a-d切换能力的逆变器来说，zf=0时表示逆变器选择模式a运行，zf=1表示逆变器选择模式d运行。

2 主动配电网的多时间尺度优化调度模型

本文提出了一种多时间尺度多设备协调的优化调度模型，旨在应对PV出力和负荷突发波动的同时保持电网的安全电压且最大限度地减少网损。该优化调度模型框架如图3所示。

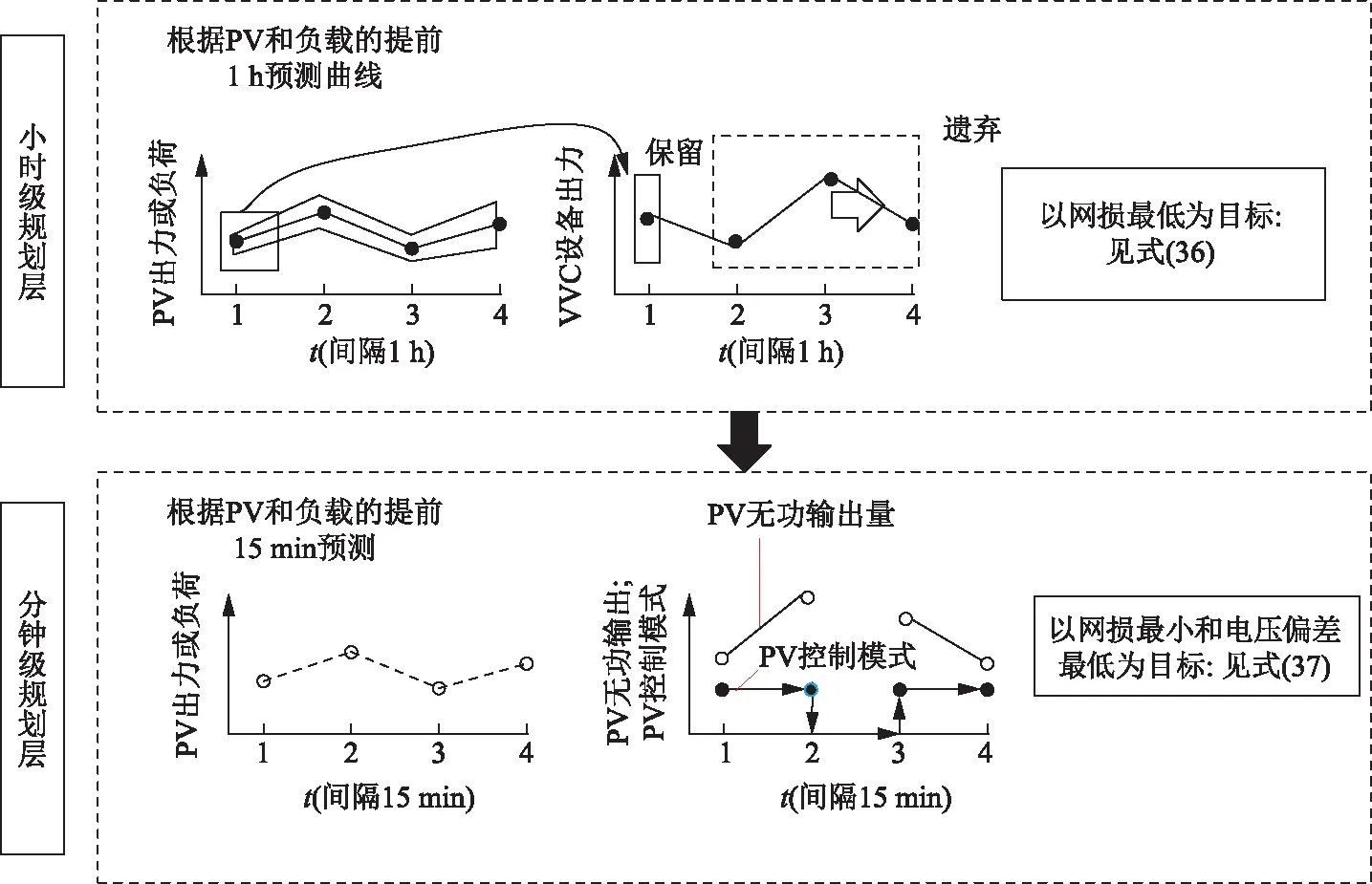
图3 多时间尺度无功优化调度模型框架Fig.3 Multi-time scaled reactive power optimization scheduling model framework

2.1 小时级优化调度阶段

在小时级优化调度阶段，预测时间尺度较长，预测精度差，如果仅按照“源-荷”预测曲线进行配电网优化调度，是难以满足配电网实际运行需求的。由此本研究选择两阶段鲁棒优化以表征“源-荷”的不确定性，从而保证小时级调度策略的有效性。

由于SC、OLTC和ESS的频繁调度会损耗其使用寿命，为避免该类设备频繁调度，本研究选择将小时级调度所求解得到的SC、OLTC和ESS策略保留下来[30]。尽管SVC属于可连续调度的电力电子设备，是可置于分钟级调度的可控设备之一，但本研究为了验证PV逆变器切换的有效性，选择将SVC作为小时级调度策略保留下来，与SC、OLTC和ESS一并为分钟级调度做支撑，让PV逆变器模式切换作为分钟级调度中的唯一可控设备。滚动优化是选择每4 h为调度周期的滚动优化，但是只有第1个小时的调度策略被保留，剩下3 h的策略均被丢弃；第2个小时的调度策略由新一轮以4 h为周期的优化计算获得。

小时级调度的目标函数为网损最小，即

(36)

式中：j与i是相关联节点；f1为配电网网损；N为配电网的节点数；Δt为调度间隔时长。

该阶段约束为式(1)—(21)、式(23)、(24)、式(26)—(30)、式(33)—(35)。

本研究采用C&CG方法进行鲁棒优化计算，详细计算步骤见第3章。

2.2 分钟级优化调度阶段

分钟级优化调度阶段预测时间尺度短，精度高，所以在分钟级调度时间尺度下，选择传统确定性优化方法进行配电网无功调度求解。根据对15 min后的PV出力和负荷的预测，调整PV逆变器的控制方式和无功出力以稳定系统电压水平和减少网损。该分钟级优化调度阶段的目标函数为

(37)

式中：ω1、ω2均为权重系数；Uref为参考电压值，本文中取1.0(标幺值)。

分钟级调度约束为式式(1)—(7)、(23)、(24)、式(26)—(30)、式(33)—(35)。

3 含可控PV的两阶段鲁棒优化求解方法

小时级调度是含有不确定性量的鲁棒优化问题。将原数学问题分解成min主问题和max-min子问题，并采用C&CG算法进行求解。其基本原理是：min主问题是基于max-min问题所产生的恶劣场景进行决策为模型提供下界，max-min子问题是根据min主问题的决策为模型提供上界。因此，两阶段鲁棒优化是针对极端场景进行优化，具有极强的鲁棒性。

本研究将用于选择PV逆变器的二元变量集合Z加入到鲁棒优化的第1阶段变量之中，并令其在鲁棒优化求解过程中总是受到新加入的列约束限制。用矩阵Z表征PV切换变量集合{zf∈{0,1},zg∈{0,1}}，用矩阵z表征zf和zg，用矩阵Λ表征光伏及负荷不确定性集合{Pj,min≤Pj≤Pj,max,Ppv,out,min≤Ppv,out≤Ppv,out,max}，则两阶段鲁棒优化模型为

(38)

鲁棒优化第1阶段为min问题；鲁棒优化第2阶段为max-min问题，本研究利用强对偶定理和外逼近法(outer approximation method，OA)[30-31]将max-min问题转化为可求解的线性规划问题，以此得到第2阶段的最优解。

本文的两阶段鲁棒优化算法流程如图4所示。

图4 两阶段鲁棒优化的C&CG及OA法求解流程Fig.4 Solution flowchart of C&CG and OA algorithms

第1阶段不等式约束Ax≤b对应式(6)—(7)、式(9)—(11)、式(13)—(16)、式(21)、式(34)，其中用变量x表征Qsvc、Qsc、Pdch、Pch、Qpv，out和Ppv，out；第1阶段PV切换约束zx≤Z对应式(29)、式(30)、式(35)。第1阶段等式约束Bx+Iyk*+Juk*=j对应式(1)—(6)、式(8)、式(12)、式(18)—(20)、式(26)，对偶变量为π1。

第2阶段不等式约束Fy≤f对应式(17)，对偶变量为π2，其中用变量y表征Qsvc。二阶锥约束‖Ax‖2≤hy对应式(5)、式(27)、式(33)，对偶变量分别为π3和π4。

4 算例分析

4.1 算例介绍

本研究选择在如图5所示的改进IEEE 33节点系统中进行仿真计算。负荷和PV出力预测曲线如图6所示，负荷和PV出力的波动范围均设置为[0.85，1.15]。将根节点的电压设为1.0(标幺值，下同)，其余节点电压为0.9～1.1；每条支路最大电流500 A；在10号节点和33号节点分别安装7组电容器，每组无功容量为75 kvar或80 kvar；在18号节点安装1组储能电池，容量为600 kWh，充放电功率为120 kW，充放电效率为90%；在9号节点安装可在模式a和模式b之间切换的PV逆变器，在18号节点安装可在模式a和模式d之间切换的PV逆变器，分别在25、33号节点安装控制模式a、模式c的PV逆变器。假设PV的最大装机容量为200 kW，逆变器视在功率为装机容量的105%，则它可以输出的最大无功功率为96 kvar。14号节点和33号节点安装SVC，补偿容量为-300～300 kvar；OLTC设置5档，每档变比为0.1。

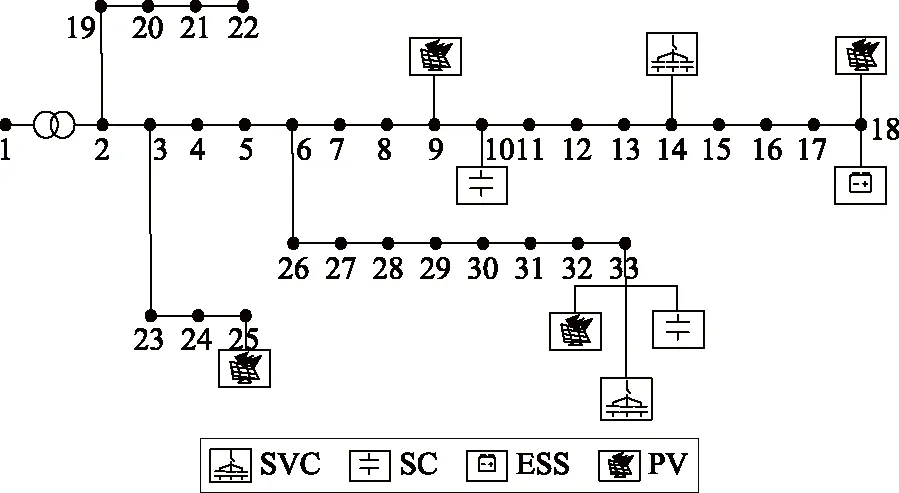
图5 改进的IEEE 33节点系统Fig.5 Improved IEEE 33 buses system

图6 PV出力与负荷的预测曲线Fig.6 PV power and load forecast curves

在配置为CPU 2.30 GHz、内存16.0 GB、工作环境为Windows10系统的电脑上，基于MATLAB平台编码，通过Yalmip调用Gurobi求解器对该算例进行求解。

4.2 小时级调度结果

小时级调度阶段首先是基于PV有功功率以及负荷需求的不确定区间，并同时考虑PV逆变器的控制模式，进行两阶段鲁棒优化，获取在该阶段PV逆变器控制模式下OLTC、SC的档位以及ESS、SVC的调度策略，调度结果如图7、8所示。

图7 SC和OLTC的小时级调度策略Fig.7 Hourly scheduling strategies of SC and OLTC decision

图8 SVC和ESS的小时级调度策略Fig.8 Hourly scheduling strategies of SVC and ESS decision

4.3 分钟级调度结果

在分钟级调度阶段，将保留基于小时级调度的SVC、ESS、OLTC和SC的策略，并在给定PV输出和负载需求的短期预测(时间间隔为15 min)基础上，对PV逆变器的模式和无功输出进行调度。4个PV逆变器中，25号和33号节点的PV逆变器分别设置为模式a和模式c，其输出无功为0，9号和18号节点的PV逆变器分钟级调度无功输出如图9所示。

图9 PV逆变器的分钟级调度结果Fig.9 Minute level scheduling of PV inverter

为验证PV逆变器分钟级调度控制的优势，现将PV逆变器完全不参与无功控制、PV逆变器仅参与小时级调度无功控制与本文所提方法进行比较，网损及电压曲线如图10、11所示，网损、电压平均值及电压偏差对比结果见表1。

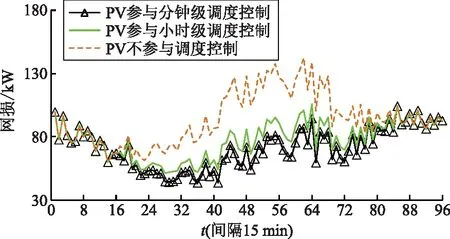
图10 3种调度策略的网损曲线Fig.10 Network losses of three strategies

图11 3种调度策略的电压曲线Fig.11 Voltage curves of three strategies

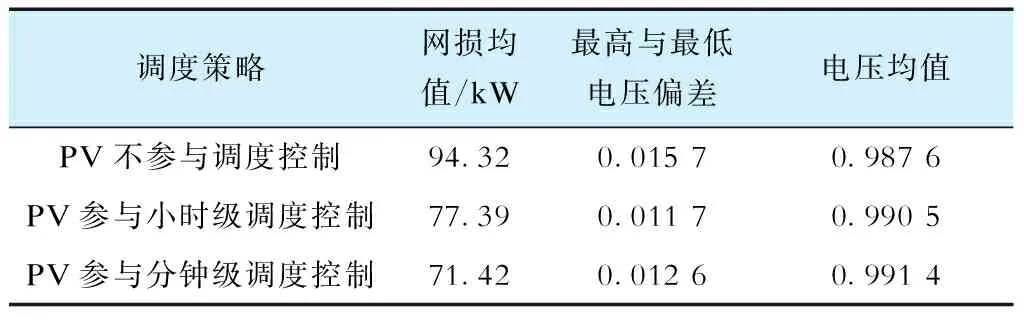
表1 3种调度策略的对比Tab.1 Comparisons of three scheduling strategies

由表1调度结果对比可知，在分钟级调度中考虑PV逆变器的控制，系统网损降低明显，相较于PV不参与调度控制，网损降低了24.27%，相较于PV仅参与小时级调度控制，网损降低了7.71%，说明了本文模型的经济性。同时，系统平均电压偏移明显降低，进一步说明本文模型能有效保证配电网系统安全性与稳定性。

4.4 鲁棒性分析

将本文方法与随机优化方法做对比分析，以说明本文方法的鲁棒性。其中随机优化过程为：首先采用正态分布随机生成200个日常场景以模拟“源-荷”的不确定性，在场景生成中，负荷和PV出力的标准差均为5%；再从其中抽取无优化网损最大的场景进行小时级调度，保留其SVC、SC、ESS及OLTC结果，并加入分钟级调度得到场景法调度结果。将场景法调度结果与本文优化调度结果做对比，网损及电压曲线如图12、13所示，网损、电压平均值及电压偏差对比结果见表2。

图12 2种优化方法的网损曲线Fig.12 Network losses of two optimization methods

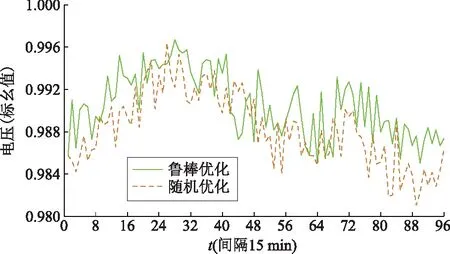
图13 2种优化方法的电压曲线Fig.13 Voltage curves of two optimization methods

由表2的优化方法结果对比可知，采用多时间尺度鲁棒优化策略时，系统具有更低的平均网损和偏移更小的电压值，说明了多时间尺度鲁棒优化策略具有更好的经济性、安全性和鲁棒性。

表2 2种优化方法的对比Tab.2 Comparisons of two comparison methods

5 结束语

为了应对“源-荷”的不确定性，本研究建立了含可控PV逆变器的主动配电网多时间尺度鲁棒优化调度模型，以实现主动配电网“源-储-无功设备”的协调优化调度。在小时级调度阶段，建立以网损最小为目标的调度优化模型；在分钟级调度阶段充分发挥PV逆变器的控制功能，用以最大化地消除配电网欠压或过电压风险，实现配电网安全运行。本研究主要贡献如下：

a)实现可控PV逆变器加入主动配电网多时间优化，并通过无功-电压控制设备和PV协调控制实现最小化网损和稳定系统电压的目的。

b)相比于随机性优化，提出了多时间尺度优化模型能够有效应对PV和负荷的不确定性，保持系统电压稳定性。

c)从设备控制、多时间尺度、“源-荷”不确定性和仿真分析等4个角度来看，本文模型有效增强了主动配电网的调控能力。