软件成本度量方法研究*

张帆 姜月 林志超 齐鑫 李宁柠

辽宁邮电规划设计院有限公司 辽宁 沈阳 110179

1 常用软件成本度量方法研究现状

目前较为流行的软件成本度量技术有：利用专家经验进行的判定法、类比相似项目数据的估算法、采用回归函数的分析法、基于数学算法的模型估算法及PERT法等[1]。

专家判定法是根据估算专家的历史经验和主观意识，结合新项目的自身特征给出估算结果，这样的估算结果往往过分依赖于专家的判断，缺乏客观性和标准性。

类比估算法将新的软件项目与以往类似项目在使用环境、应用场景等方面的实际数据进行类比，得出一个估算值，类比结果的准确性往往依赖于以往相似项目历史数据的完整性和代表性。

回归分析法利用软件产品的历史数据来预测和估算新软件项目的估算成本，常用的有OLS、OSR、CART等回归方法，其方法简单、易用，但是回归模型需要对软件项目进行严格的假设条件，一旦出现偏差较大的参数值，就会对回归算法的估算结果造成巨大的影响。

算法模型估算法给出了一种或多种的数学方法,由这种数学方法所引起的软件成本度量，可以看作是主要成本与控制因素之间变化的函数。算法模型具体分类如下表：

虽然算法模型的发展趋势十分乐观，但其度量结果的准确性仍受制于软件项目的规模、模型因子及软件环境等因素，且目前还没有任何一个适用性及通用性很强的模型可以满足各类软件项目的成本度量。

在实际项目管理中，对于实现复杂、采用前沿技术且无相似项目可以作为经验参考的软件项目，可以采用PERT技术。PERT实现原理是假设工作的时间和完成时间都是随机的，并遵循着一定的概率分布，PERT就能够预测该工作在特定日期内可实现的可能性[2]。PERT在综合考虑项目各种可能存在风险的前提下，采用三点估计法来估算活动的持续时间，根据不同项目活动所需要的完成时间划分成3种情况进行估算：

最可能持续时间（mostlikely time）：是在已知该项目所具备的资源、资源的产出率及能够支持给该活动所需的实际可能性和依赖其余活动参与的条件下，需要的连续的时间[3]。

乐观持续时间（optimistic time）：是在最可能持续时间所有的前提条件都是最有利的时候所预估出来的持续时间。

悲观持续时间（pessimistic time）：是在最可能持续时间所有的前提条件都是最恶劣的时候所预估出来的持续时间。

根据以上公式还可以进一步计算出任一项工作的时间方差，公式为：通过平均值及方差计算得到的活动持续时间相对于单点计算获得的值要更加准确。

2 结合方差和PERT的软件成本动态调整度量方法

为解决目前常用成本度量算法及模型存在的不足，得到客观准确的度量结果，本文采用结合方差和PERTF的动态调整度量方法，其原理就是通过方差分析动态的调整度量值，然后再将PERT法融入成本度量的一种新型的成本估算。基本流程图如下图1所示。

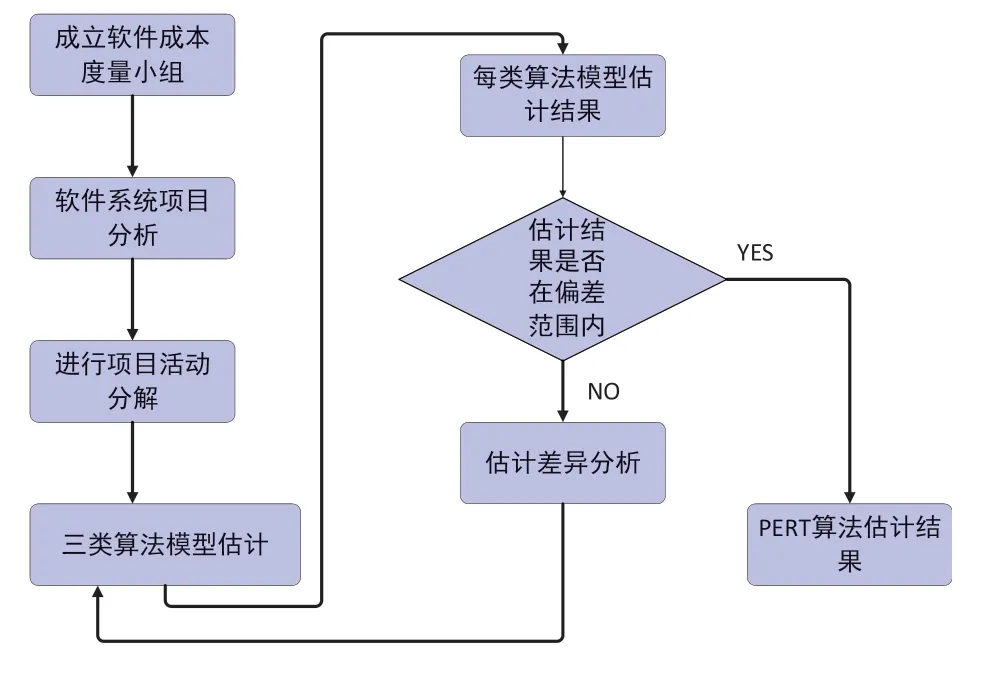
图1 结合方差和PERT的软件成本动态调整度量模型

此方法适用性广、运用方便具体实现步骤如下：

步骤1：

步骤2：

分析估计结果：项目经理对每个活动负责人的估计结果进行汇总，并对每个活动不同的成本估算算法模型计算出的成本进行分析。分析方法如下：

（1）分析每个活动中不同算法模型的估计值M与活动计算出的三点估计值之间的误差，若存在S>30%，即有一个偏差值大于所设定的偏差值标准,此时跳转执行步骤 1；

（2）此次执行步骤1时需要由所有专家参与，分析并动态的调整算法模型涉及的影响因素，重新计算该活动的成本，否则 为该活动成本的最终成本估计值；

（3）计算项目整体工期的成本值=（各活动成本的最终估计值）。

步骤3：

活动负责人将上述估计结果进行统一汇总，计算出项目成本的总估计值，确定出最终的项目成本估计值。

3 结合方差和PERT算法模型应用案例

3.1 算法模型度量成本应用案例

本文应用上述方法来完成一个软件开发项目的成本度量，将软件项目的生命周期大概分为3个主要活动：需求分析、需求设计和系统开发。各项活动通过3种不同类型的算法模型进行成本的估计，然后根据PERT方法的三点估算计算出每个活动成本的估计值。如下图所示：

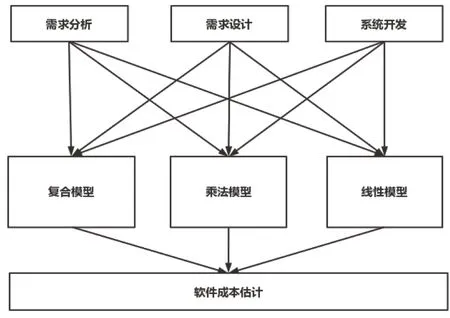
图2 软件项目活动图

设定项目的偏差标准为30%，本例在估算过程中参考了三种不同类型算法模型的成本估算数据。本例中选择不同类型的算法模型分别是：复合模型中的COCOMOⅡ模型、乘法模型中的Bailey Basili模型和线性模型中的SDC模型[3]。活动成本估算结果如表2所示：

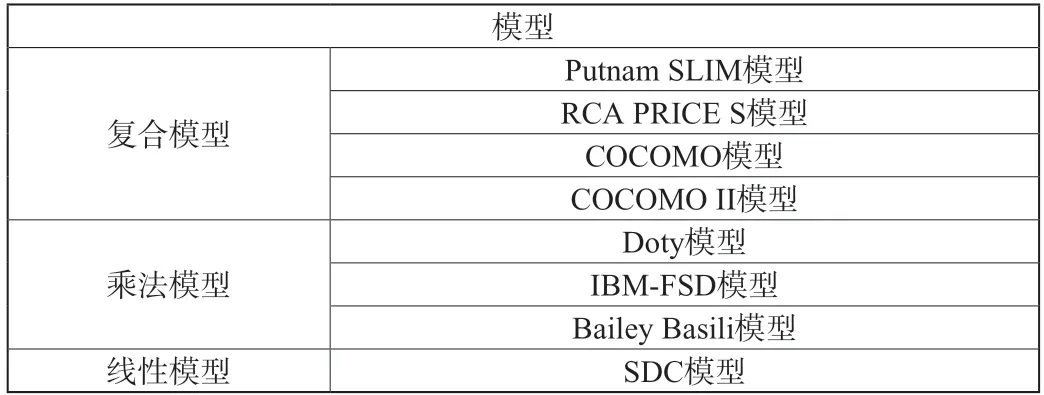
表1 算法模型分类表

表2 活动成本估算表

以表中1中 “需求分析”的数据为例，对其最终的估计结果进行计算。

对于需求分析活动而言，每个估算模型的估计值与三点估计值之间的偏差的绝对值分别为：2，2，0。因为所以需求分析活动的其他两个算法模型的S分别为：15%，0，均在偏差标准30%之内。所以该为该活动的最终成本估计值，即该活动的最终估计成本估计为13。以此类推，其他活动的每个算法模型的S也都在偏差标准30%之内，因此需求设计和系统开发的最终成本估计值分别为：68，99。因此，可得项目的总工期为t=t1+t2+t3=13+68+99=180人天。

3.2 算法模型度量成本的准确度分析

计算得到以上3个活动的期望成本和标准差为：

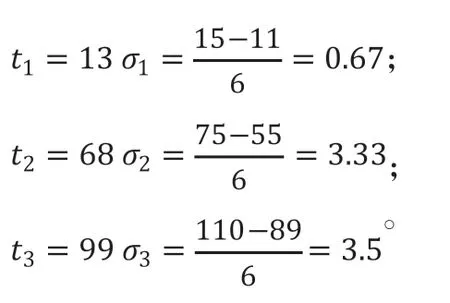
根据概率理论，每个活动消耗的成本服从正态概率分布；举例说明：系统开发活动的期望成本为=99，其方差为=3.5；则根据上面的数据，可以得出成本在范围内即95.5与102.5之间，完成项目的概率为68%；成本在范围内即在92与106之间，完成项目的概率95%；成本在范围内即在88.5与109.5之间，完成项目的概率为99%。系统开发的三个算法中Bailey Basili模型估计成本110大于=109.5，说明Bailey Basili模型算法计算出的成本对于系统分析而言估算准确度比较高；需求分析活动中COCOMOⅡ模型算法计算出的成本值准确度比较高；需求设计活动中三个算法中Bailey Basili模型估计成本55小于=58.1，在此成本下完成的概率几乎为0，因此Bailey Basili模型不适用于需求设计活动，估算成本值的准确度比较低；通过算法模型的准确度的判断，可以分析出每个算法模型适用的活动类型，具有项目成本度量估算的参考价值；例如本文中所举案例的估算出得的成本是180，而项目最终实际成本为185，其误差在5%之内，因此估算方法是切实可行的。

4 结束语

本文研究的方差分析和PERT方法结合的动态调整技术，将不同类型的度量算法模型一起计算得到估算的成本，从而提高了度量成本的准确性及灵活性，而且还可以得出每个算法估算模型最为适用的活动。最后本文按照算法的理论原理，以一个实际项目为例子进行了验证，通过实验结果可以看出，在软件成本度量的准确性上本文介绍的方法明显优于其他算法模型，通过算法计算得到的成本度量结果与实际成本之间的偏差最小，用数据结果证实了该算法的准确性。