基于泊松多伯努利混合滤波器的新生目标跟踪

鑑美玉 柳晓鸣

(大连海事大学信息科学技术学院 辽宁 大连 116026)

0 引 言

多目标跟踪(Multiple Target Tracking，MTT)包括处理从多个目标获得的量测集以及估计目标的当前状态[1-3]。解决MTT的难点在于目标和量测之间未知的对应关系。已有的MTT方法有联合概率数据关联(Joint Probabilistic Data Association，JPDA)滤波器、多假设跟踪器(Multiple Hypothesis Tracker，MHT)和基于随机有限集(Random Finite Sets，RFS)的算法[4]。Mahler基于RFS理论提出了概率假设密度(Probability Hypothesis Density，PHD)滤波器，PHD在现阶段依旧被应用在目标跟踪研究中[5]，接着Vo等提出了基数概率假设密度(Cardinalised Probability Hypothesis Density，CPHD)滤波器，如文献[6]应用和高斯概率假设密度(Gaussian Mixture Probability Hypothesis Density，GM-PHD)滤波器[7-8]。

研究发现，PHD滤波器可以处理目标的新生、存活和死亡。但是对于新生目标的处理必须要求新生目标强度已知，在处理问题时往往假设其已从量测中获得并已知。PHD滤波器缺少在本质上检测新生目标的功能，而新生目标的检测是多目标跟踪中重要部分。针对新生目标跟踪问题，García-Fernández等[9]提出泊松多伯努利混合(Poisson Multi-Bernoulli Mixture，PMBM)滤波器，并利用文献[10]中的概率生成函数(Probability Generating Functionals，PGFS)和函数导数推导出了基于共轭先验性质的PMBM滤波器。本文将其应用于新生目标跟踪研究中。

在MTT滤波中，考虑共轭先验是有优势的，在共轭先验中，后验分布可以明确地写成单目标贝叶斯更新的形式。PMBM滤波器的共轭先验由泊松过程和多伯努利混合(Multi-Bernoulli Mixture，MBM)的并集构成。泊松部分表示在无杂波下从未检测到的目标(新生目标)，MBM部分表示至少检测过一次的目标(生存目标)。全局数据关联就是单目标的数据关联，每一个目标量测都只对应于一个目标，并且指定了目标基数上的分布而不是唯一基数。

本文提出一种基于PMBM滤波器的新生目标跟踪方法。针对多目标无虚警研究，不需要假设新生目标先验信息已知，仅根据量测信息来构建新生目标的强度信息。跟踪的简要流程为根据量测信息将泊松过程的量测构建为新生目标，将符合MBM的量测建立存活目标，并将两者分别进行预测、更新和修剪。并将本文算法与传统GM-PHD算法进行对比。

1 泊松多伯努利混合模型

1.1 泊松多伯努利RFS模型

基于RFS的方法中，目标状态和观测值以有限集的形式表示。系统在k时刻的状态被建模为一个集合Xk，在k时刻得到的一组测量值记作Zk，包括杂波、目标产生的量测和未知的量测来源。到时刻为止接收到的所有测量集的序列记作[4]。

强度函数为λ(x)的非齐次泊松点过程(Poisson Point Process，PPP)的RFS密度函数为[12]:

(1)

式中：x为单个目标的状态；X为多个目标的状态；|X|为集基数表示泊松分布；x∈X为独立同分布。泊松过程常用于未标记的RFS滤波器中的杂波和新生目标建模。

存在概率r和存在概率密度函数f(x)的伯努利过程的RFS密度函数为：

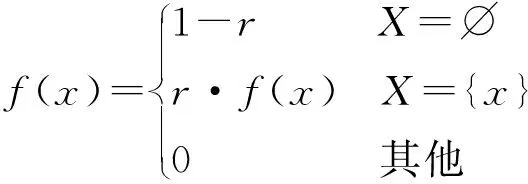
(2)

式中：|X|为集基数服从参数为r的伯努利分布。标记的伯努利随机有限集X是一个伯努利随机有限集X和标签l的增广组成对应于非空的伯努利分量x，X={(x,l)}或X=∅。伯努利过程可以获得目标存在和状态的不确定性，它也被用于标记RFS滤波器来模拟新生目标。

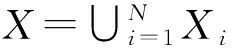
(3)

1.2 贝叶斯滤波器递归

根据文献[6]，可以用基数分布c(n)和联合条件状态分布fn(x1,x2,…,xn|n)表示为:

(4)

式中：xi是x的第i个分量。并且带标签的RFS和不带标签的RFS具有一样的基数分布。

在式(4)所示的k时刻的多目标分布，在给定k′时刻的所有量测条件下，k时刻的状态集合的似然函数为fk|k′(Xk|Zk′)，fk(Zk|XK)为k时刻量测的似然函数。根据文献[4]，贝叶斯滤波器的状态更新似然函数为:

fk|k(Xk|Zk)∝fk(Zk|Xk)fk|k-1(Xk|Zk-1)

(5)

式中：∝表示约等于。

贝叶斯滤波器状态预测似然函数表示为：

(6)

贝叶斯滤波器的积分集合为：

xn})d(x1,x2,…,xn)

(7)

1.3 标准化点目标转换和量测模型

解决基于RFS的MTT问题的动态点目标转换模型有以下假设[12]：

新生目标根据PPP过程建立，独立于生存目标。在每个时间步长目标保持生存概率Ps(x)。目标下一时刻的状态只取决于当前时刻的状态。目标运动遵循独立同分布马尔可夫过程，其状态转换密度为fk|k-1(xk|xk-1)。

多目标模型的转移概率

(8)

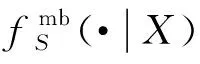
建立量测模型有以下假设：

每个目标生成的量测只对应于相应的目标，单目标量测似然函数为fk(zk|xk)。在每个时间步长中可能检测到目标也可能检测不到，目标检测概率为Pd(x)。该传感器可以接收非目标(杂波)的测量(虚警)。在每个时间步长，杂波服从PPP强度为λc(z)，独立于目标和目标生成的量测。

多目标量测模型的似然函数可以用卷积形式表示[12]：

(9)

式中：Tk是k时刻目标生成量测；Ck是k时刻杂波量测。

1.4 泊松多伯努利混合滤波器

根据文献[10]，MTT的PMBM过程的RFS密度函数是独立PPP和MBM分量的线性组合，其形式可表示为：

(10)

(11)

每个数据关联假设都是由单个目标假设{h1,h2,…,hN}对应每个目标。假设存在但从未被检测到的目标被视为未知目标，用PPP分布表示。

在预测步骤中，描述已有轨迹的MBM和描述未知目标的PPP分别被单独预测。通过建立泊松出生模型，可以将新生目标的PPP合并到预测的PPP中。在更新步骤中，PPP和MBM是独立更新的。为每一次量测建立两个单目标假设，然后通过漏检概率更新PPP强度。

2 线性高斯PMBM滤波算法

2.1 背景假设研究

在文献[9]的共轭先验概率中，MBM有一个指标j。j对应一个全局假设，表示测量值与潜在目标之间可能存在的关联。全局假设可以用单目标假设来表示。单目标假设对应于每个可能探测到目标相关的一系列测量。给定一个单目标假设，这个可能被探测到的目标遵循伯努利分布。因此，每次测量都开始于一个新的单目标假设[13]。在接下来的时间步长中通过将以前的单目标假设与当前的测量值或误检值联系起来去创建新的单目标假设。在没有不相关的量测并且一个量测只能分配给一个单一的目标假设下即全局假设是这些单目标的集合。

目标状态估计选择式(11)的MBM全局假设中最大的权重，则获得的指标为：

(12)

式中：j*的伯努利分量均值的存在概率大于阈值Γ。

2.2 预 测

假设在前一个时间步长的后验中，泊松分量强度的后验高斯混合密度为：

(13)

(14)

(15)

式中：FT为F的转置。

2.3 更 新

(16)

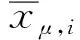
从共轭先验更新中得到三种不同类型的更新：未检测到目标的更新(泊松分量)，第一次检测到的潜在目标更新和已检测到的目标更新。泊松部分的更新比较容易。将未检测目标的更新强度式(16)乘以1-pd。

(1) 第一次检测到的潜在目标更新(新生目标)。首先遍历所有的泊松先验，并对量测值上执行椭球形门控如文献[9]选择，以降低计算复杂度。对于那些可以根据门控输出新轨迹的量测，我们执行贝叶斯更新。z为量测，并给出了rp(z)存在的伯努利分量和目标状态密度函数pp(x|z)如：

rp(z)=e(z)/ρp(z)

(17)

pp(x|z)=p(z|x)μ(x)/e(z)

(18)

其中：

(19)

ρp(z)=e(z)+c(z)

(20)

式中：c(·)为杂波量测；e(z)为存在量测。为了降低计算复杂度，将式(19)中的高斯混合函数近似为高斯函数，并进行矩阵匹配。确定新创建的MBM的假设权值，ρp(z)是假设权值wj,i首次在全局假设j下检测到潜在目标测量z。如果全局假设j不考虑这个可能被探测到的目标wj,i=1，则将其存在概率设为0。

(2) 已检测到的目标更新(生存目标)。通过式(11)的遍历创建单一目标的假设，rj,i为全局假设为j的第i个目标的生存概率，wj,i为全局假设为j的第i个目标的权重。可得已检测到的目标的高斯概率假设密度为：

(21)

2.4 基于k-Best方法全局假设的选择

对于每一个全局假设j在前一个时间步长中，必须通过所有可能的数据关联假设，从而产生更新的全局假设。这种全局假设的大量增加是共轭先验计算的瓶颈。然而，基于标记RFS和MHT的文献，通过使用Murty算法[15]修剪假设的数量来近似这一更新。通过该算法，可以在不评估所有新生成的全局假设的情况下，为给定的全局假设j选择权值最高的k个新的全局假设。对于全局假设j，所有的量测(不包括门限滤除量测)必须与全局假设j中的现有轨迹相关联或与一个新轨迹相关联，并且没有未分配的测量。然后利用共轭先验的更新权值构造相应的代价矩阵。假设通过门限后在全局假设j中有n0个旧轨迹，m个量测z1,z2,…,zm。代价矩阵为：

C=-[ln(Wot,Wnt)]

(22)

式中：Wnt=diag(ρp(z1),ρp(z2),…,ρp(zm))，Wnt表示潜在检测目标的权值矩阵；Wot∈Rm×nj表示生存目标的权值矩阵，nj为全局假设j中前一时刻潜在检测到的目标个数。Wot中的p、i表示第i个目标相关联的第p个量测。Wot为:

(23)

2.5 线性高斯PMBM算法流程

步骤1根据当前时刻量测集Z和前一时刻PMBM后验参数得到当前时刻PMBM后验参数。

步骤2进行多目标预测。

步骤3进行多目标运动状态更新。

步骤4修剪。剪去权值低于阈值的成分来修剪泊松部分。保持Nh最大的全局假设来修剪全局假设。删除存在概率低于阈值或不出现在修剪后的全局假设中的伯努利分量。

3 仿真实验

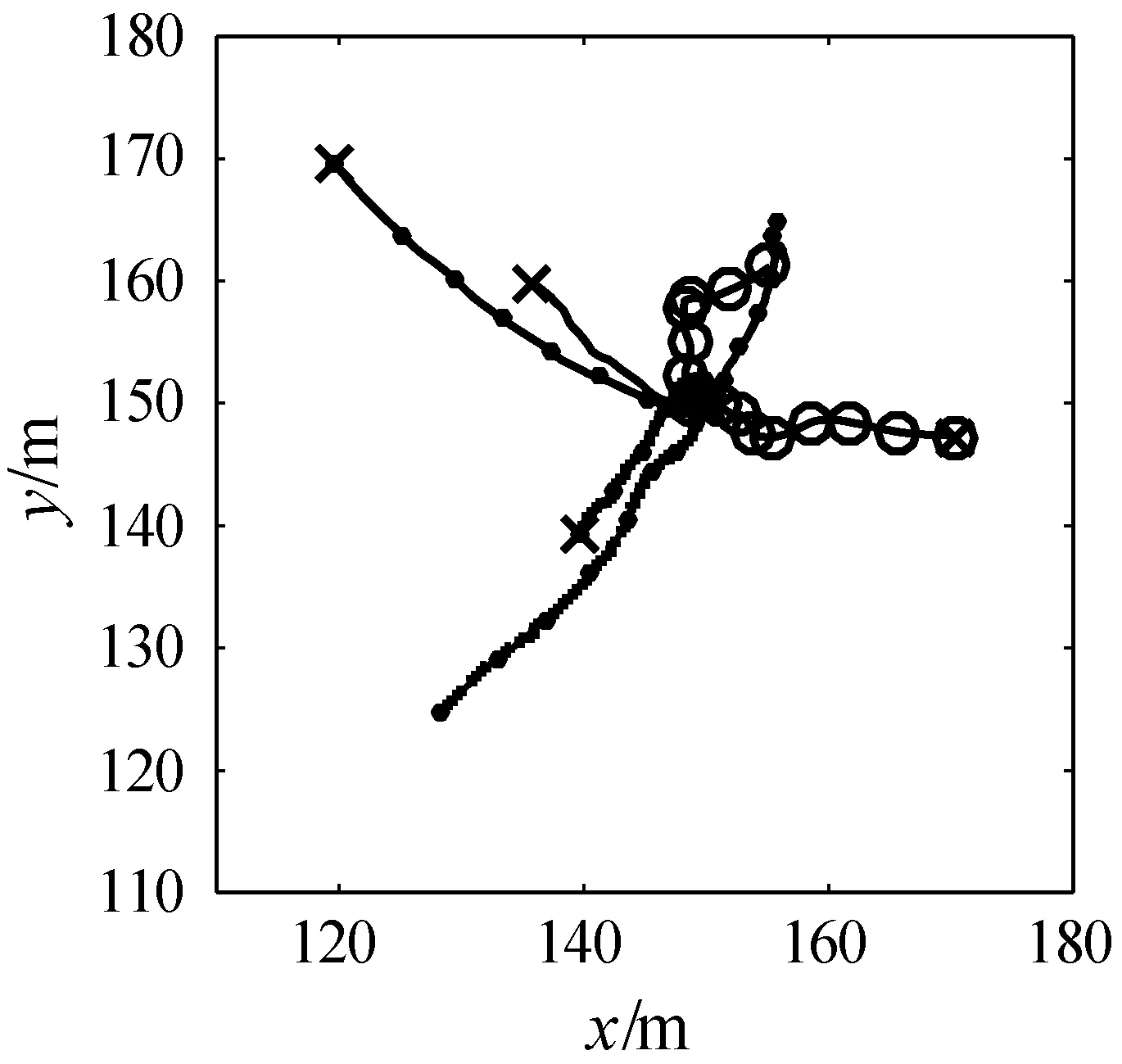
图1 目标真实轨迹

(a) RMS GOSPA误差

(b) RMS GOSPA 位置误差

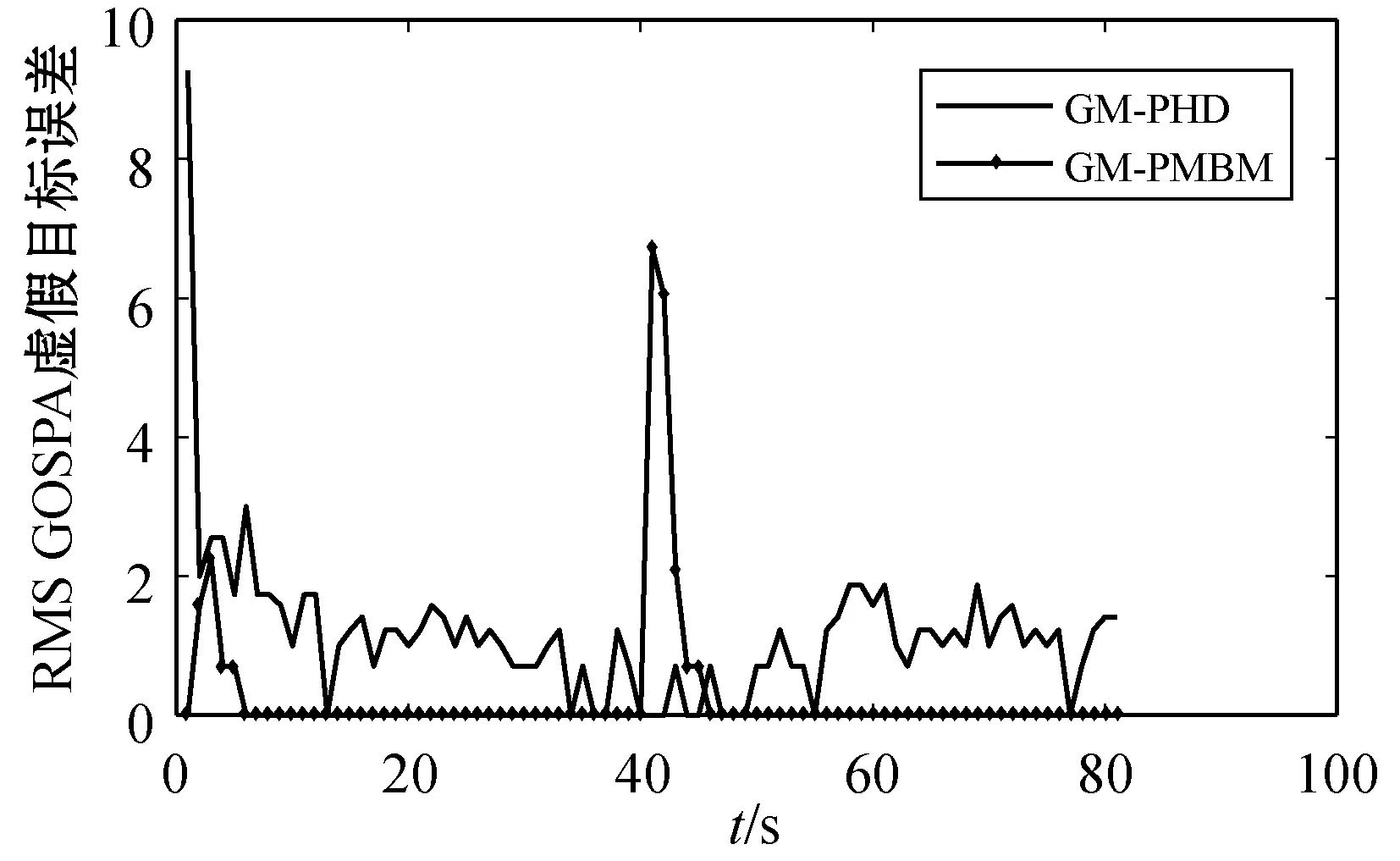
(c) RMS GOSPA 虚假目标误差

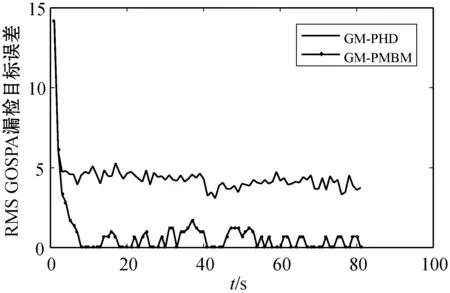
(d) RMS GOSPA 漏检目标误差图2 GOSPA均方根四种误差算法对比

表1给出了两种算法GOSPA四种参数的对比。在本文算法GOSPA的误差均方根减少47%，位置误差均方根减少24%，错检目标误差均方根减少32%和漏检误差均方根减少57%。仿真结果显示，本文算法不仅跟踪精度有所提高，而且还分别针对不同误差进行对比，可以进一步研究更好改进途径。

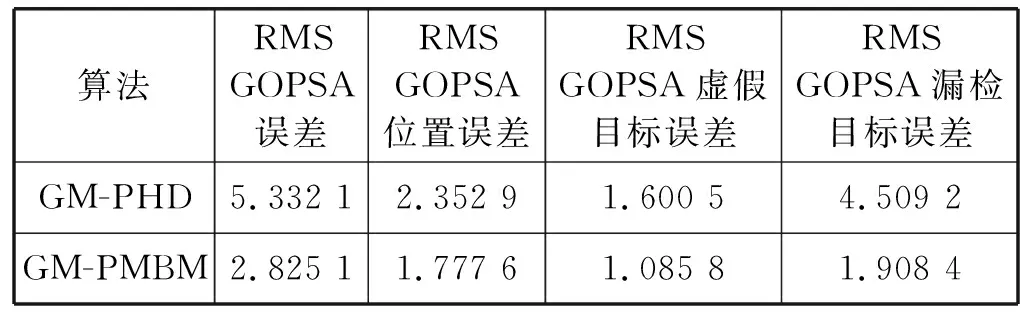
表1 GOSPA均方根误差算法对比

表2给出了两种算法时间上的对比。从平均每次运行时间可看出，本文算法时间消耗为传统GM-PHD的4.55倍。GM-PHD需要新生目标的先验信息，不需要重新去构造出新生目标的强度，从而在时间上应用减少。但是需要先验信息的假设是不合理的，严重依赖先验信息，容易产生较大误差，从而限制了其应用。本文算法以时间消耗为代价提高了目标的跟踪性能。本文应用MATLAB仿真没有进行算法优化，下一步以计算机的并行处理此方面进行时间改进途径。

表2 两种算法运行时间对比 单位:s

4 结 语

针对传统GM-PHD滤波算法需要先验的新生目标强度，提出基于PMBM滤波算法。该算法由泊松过程和多伯努利混合形式的并集组成，将当前时刻量测划分为新生目标量测和存活目标量测，并且分别进行线性高斯形式的泊松强度的新生目标和多伯努利混合分布的生存目标预测、更新和修剪。从实验仿真效果来看，本文算法可以在新生目标未知的情况下有效地进行跟踪，其跟踪精度、误差优于传统的GM-PHD滤波算法。接下来可以用该算法去解决航迹初始建立问题和形成问题。