基于离散元法的磨机径向和轴向级配钢球运动与偏析模拟

周钰锦 庄故章

1(南京邮电大学物联网学院 江苏 南京 210023) 2(昆明理工大学国土资源工程学院 云南 昆明 650093)

0 引 言

离散单元法(Discrete Element Method，DEM)是20世纪70年代初由Cundall等[1]提出来的一种针对复杂非连续系统动力学问题的新型数值分析方法。20世纪90年代，国外的研究者将离散元法移植到研究球磨机的工作过程[2-4]。国内大约在2007年前后，昆明理工大学的迟毅林、董为民为本校培养了第一批该方向上的研究生[5-6]。之后，国内涉及到该研究方向的各高校、各设备制造企业和公司，纷纷开展了离散元法用于球磨机工作过程的研究，并取得了不少的成绩[7-10]。

毋庸置疑，球磨机工作过程的好坏，取决于磨机内钢球的运动状态，钢球的运动状态又受转速率、充填率、衬板形状、钢球尺寸、钢球配比、矿浆浓度等因素的影响[11]。自采用离散元法作为研究工具以来，研究者除对上述宏观因素深入研究外，还涉及到了以前因缺乏有效工具不可能开展研究，而今成为了可能的研究，比如，任一钢球在任意时刻的运动轨迹、钢球与钢球之间和钢球与周边环境之间的受力、碰撞、能量转变、球磨机功率大小等机理层次的研究，一步一步在探索球磨过程的本质[12-15]。

球磨机由圆筒和两个端盖组成，圆筒内装有钢球介质。上述研究，就圆筒方向而言，无论是采用传统研究方法，或者是采用现代研究手段，研究者主要从事在筒体直径断面上进行钢球运动状态研究，符合主体需求。就使用钢球来看，基于离散元法的研究者采用单一直径钢球研究运动状态居多，采用不同直径和配比的级配钢球少，但级配钢球更符合实际工作状况。从球磨机筒体径向断面来看，早期的研究把钢球的运动分为泻落、抛落、离心三种典型运动状态。泻落以研磨物料为主，抛落以冲击物料为主，离心没有磨碎物料的作用。以抛落为主实际运行的球磨机中装有不同尺寸的级配钢球和粒度不同的物料，钢球的直径愈大，质量愈大，冲击力就越大；钢球的直径愈小，比表面积增加，研磨作用提高。按此，理想的磨碎功能就应该是大球冲击大块，小球研磨小粒。近年来，对球磨机中钢球和物料的分布规律做的研究表明，在筒体径向，钢球和物料分布规律类似，即小球和小块物料处于最外层，越靠近磨机轴心，钢球直径和物料粒度越大，最大球和大块物料集中在“肾形区”，从而形成了钢球的分层和径向偏析。根据外层球以冲击作用为主，事实是球和物料都小；内层球以研磨作用为主，但球和物料都大。这样的分布规律对钢球粉碎物料非常不利。这种不利是由于球磨机自身工作原理缺陷所致，但如何减轻钢球的分层和径向偏析，尽管国内外学者在筒体径向也提出了钢球分布的一些计算方法和公式，但还不成熟[11]，因此，充分研究符合实际的级配钢球在筒体径向的运动状态，还有工作可做。

在筒体轴向，大小钢球与粗细物料的分布规律刚好相反，若排料端的钢球大而物料细，给料端的钢球小而物料粗，大小钢球的粉碎功能与粗细物料的粉碎需求相反，称之为钢球的轴向偏析。轻微的轴向偏析不至于影响生产，往往被人们所忽略；严重的轴向偏析会恶化生产，由于偶见，企业生产人员常常束手无策。关于钢球在筒体轴向分布的研究，文献报道极少[14]，仅限于球磨机处于连续或非连续运转时，采用高速相机拍摄钢球运动状态，停机后观察钢球和物料的分布，然后对其现象再作宏观解释和分析。至于任一时刻，级配钢球中任意一球或整体钢球在筒体轴向的运动变化规律，由于经典的数理分析推导求解复杂，又缺乏有效的研究工具，长期以来一直停滞不前，几乎没有研究。虽然钢球的轴向偏析偶见，但一旦发生又无求解举措，会影响生产，为防患于未然，故有必要研究。

综上所述，为解决前述问题，本文拟采用离散单元法作为研究工具，以符合实际工况的级配钢球作为研究介质，通过模拟，进一步研究钢球在筒体径向的运动状态，探索并开启钢球在筒体轴向运动规律趋势性研究，完善球磨机的工作过程。

1 球磨机和钢球的离散元模型建立

1.1 离散元模拟参数的确定

球磨机和钢球的离散元模型建立是以黄鹏、何亮前期研究为基础的[5-6]。目前国际上应用比较广泛的离散元软件有多个版本，其中PFC是首个离散元商业软件，适于研究大量颗粒的总体流动、颗粒的破裂和动态破坏等问题，本文采用PFC3D软件进行球磨机中钢球介质的运动模拟。为便于分析，假定钢球颗粒为刚性体，颗粒本身不能产生变形，由此PFC3D软件将静力分析和动力分析两者均用牛顿第二定律来表达。采用试参法，通过改变阻尼系数使模拟值更接近理论值。在仿真模拟之前，还需设置一些参数，见表1。

表1 PFC3D模拟计算相关参数

参数设定需要说明两点：(1) 实际工作中，球磨机的充填率大约在30%～50%，摩擦系数约为0.35～0.60。本文模拟的球磨机充填率在正常范围内，但未加入物料和水，模型中也没有使用提升块，为了使磨矿介质有足够的提升力，并保持介质不滑动，使模拟结果更接近实际，通过适当增大摩擦系数来减小滑动量。(2) 采用与实验研究相同的条件，磨机直径为450 mm，筒长450 mm，钢球尺寸和钢球配比方案见表2。

表2 钢球尺寸和配比

1.2 球磨机和钢球的离散元模型

适合离散元模型的磨机可以简化为由一个圆筒和两个端面组成，如图1(a)所示。筒体两端有两个看不见的向量平面，构成一个封闭的边界模型，球磨机的筒体模型即为数值模拟的边界条件。随后生成的颗粒(钢球)集合被限定在筒体模型内运动，刚生成的钢球充满了整个筒体，各钢球之间没有接触，还处于非平衡状态，如图1(b)所示。当对钢球施加重力加速度后，钢球在重力作用下以自由落体运动下落到筒底，最终达到初始平衡状态，见图1(c)。

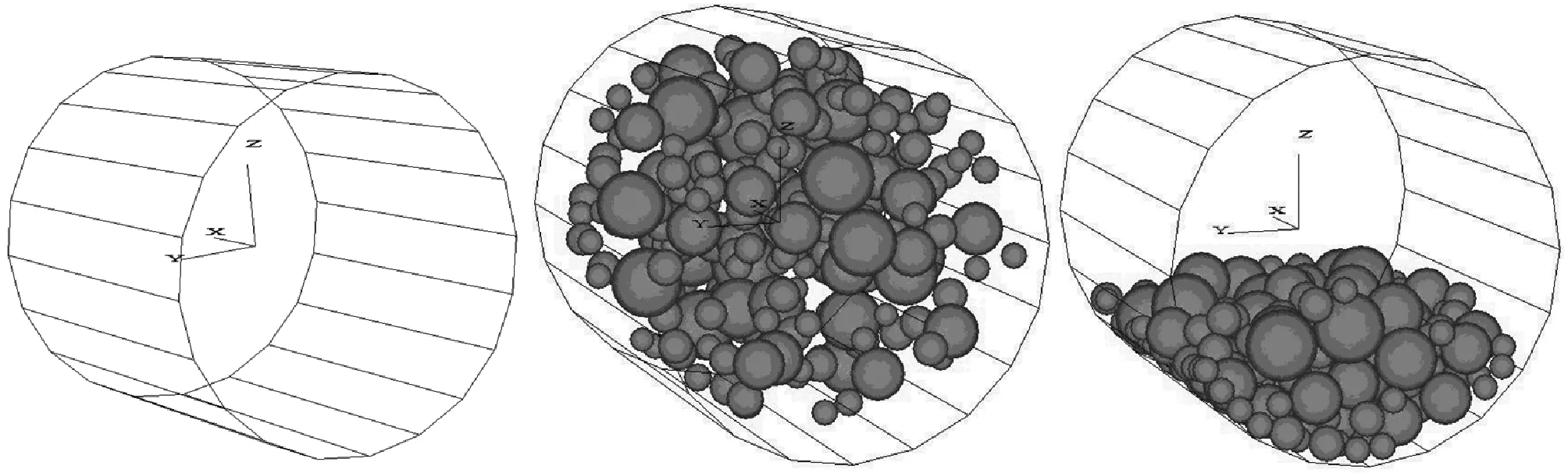
(a) 球磨机筒体模型 (b) 非平衡状态钢球模型 (c) 初始平衡状态钢球模型图1 球磨机筒体和钢球模型

图1中的坐标按如下方式定义：X轴平行于筒体中心线，Y和Z均与筒体中心线垂直。

2 钢球径向运动模拟结果与分析

球磨机正常工作时，充填率φ为磨机容积的30%～50%，转速率ψ变化范围一般为76%～88%，采用不同充填率和转速率组合方案时，钢球运动轨迹基本类似。表3是充填率φ为40%时，不同转速率下级配钢球某一瞬间的运动截图，D为钢球直径。ψ=0%时，空隙率为0.436 5；ψ=76%时，空隙率为0.635 1；ψ=100%时，空隙率为0.483 2。

表3 不同转速时级配钢球和单一钢球运动模拟(φ=40%)

续表3

由表3可以看出：(1) 转速率ψ=0%时，钢球处于静止状态，此时钢球为密堆积，空隙率最小，大钢球有靠近磨机中心的趋势，而小钢球有远离磨机中心靠近筒体的趋势，钢球属自然分层和偏析。(2) 转速率ψ增加到76%时，空隙率增加，钢球的偏析和分层趋势越加明显，大钢球主要靠近磨机中心，小钢球主要分布于筒壁，此时钢球处于典型的抛落运动状态。(3) 当磨机的转速为临界转速，即转速率ψ=100%时，钢球进行离心运动，空隙率降低。(4) 钢球作抛落运动时，模拟结果为小钢球和小颗粒物料在外层，大钢球和大颗粒物料在内层。根据外层球以冲击作用为主，内层球以研磨作用为主的粉碎特性，又根据理想的磨碎功能是大球冲击大块，小球研磨小粒。但此时钢球的行为是小球冲击小粒，大球研磨大块物料。所以级配钢球的运动分层和径向偏析导致了大小钢球的粉碎功能与被磨碎物料粒度特性相矛盾。要减轻这种矛盾，可以用几种不同规格的钢球，经计算各钢球直径能确保各级物料所需的破碎力后[11]，尽量减少大钢球与小钢球的直径差，并按一定比例搭配使用，从而可改善物料的磨碎效果。(5) 由钢球作抛落运动的模拟还观察到，尽管大钢球运动轨迹更靠近磨机中心，抛落高度低，但作抛落的概率和次数比小钢球要多得多，这对大颗粒物料的破碎具有直接促进作用；虽然小钢球抛落几率和次数均小于大钢球，但其轨迹更靠近筒体壁，小钢球与筒体和小钢球之间由于公转和自转对物料也有研磨作用。

3 钢球轴向运动模拟结果与分析

传统理论基本上没有论述钢球在球磨机筒体轴向偏析的，在轴向偏析主要表现为钢球X轴方向的位置发生改变。图2是不同充填率和不同转速率下，级配钢球中某一钢球的运动位置曲线，以58号最大钢球D120 mm的运动为例，图中实线、点线、虚线三种曲线分别表示X、Y、Z轴的位置曲线。

(a) φ=30%，ψ=76%

(b) φ=30%，ψ=82%

(c) φ=30%，ψ=90%

(d) φ=30%，ψ=100%

(e) φ=40%，ψ=76%

(f) φ=40%，ψ=82%

(g) φ=40%，ψ=90%

(h) φ=40%，ψ=100%

(i) φ=45%，ψ=76%

(j) φ=45%，ψ=82%

(k) φ=45%，ψ=90%

(l) φ=45%，ψ=100%图2 不同充填率和转速率下球径D120钢球的运动位置

可以看出：(1) 当充填率φ=30%，φ=40%，φ=45%，转速率ψ从76%到100%整个区间，钢球在X轴方向的偏析几乎都是存在的，只不过偏析的程度有所不同。(2) 当充填率较低φ=30%时，随着转速率从76%增加到100%时，钢球在X轴的偏析起伏大，基本没有明显的规律性。比如ψ=76%时，钢球在X轴方向偏析不是很明显；当转速率增加到ψ=82%时，钢球在短时间内就偏析得非常明显，直到过程结束，此间钢球从X=-0.18 m偏析到X=0.18 m，偏析总长达0.36 m，几乎跨越整个磨机的长度，钢球长时间和长距离偏析，大小钢球的粉碎功能与粗细物料的粉碎需求相反，会导致磨矿过程恶化；当转速率ψ增加到90%时，钢球的位置基本没有变化，几乎没有偏析产生，磨机处于理想的工作状态；而ψ=100%时，钢球在轴向的偏析又比较明显，与ψ=82%相比，偏析开始的时间延后，偏析的距离略短，从X=-0.18 m偏析到X=0.10 m，偏析总长0.28 m。因此，在充填率较低φ=30%，转速率从76%增加到100%时，钢球在X轴的偏析起伏大，基本没有明显的规律性，操控磨机困难。(3) 当充填率适中φ=40%和φ=45%时，在转速率ψ从76%到100%整个区间，钢球的轴向偏析距离与φ=30%相比，偏析程度明显减少，偏析的轴向距离大都在X=-0.18 m到X=0.00 m内，偏析总长0.18 m，并且在偏析距离达到最大值后，又呈现缩小偏析趋势，钢球短距离偏析对生产影响不大。(4) 钢球轴向偏析是由于钢球在运动过程中，受到钢球与钢球、钢球与筒体的相互作用的综合表现。当钢球较少充填率较低φ=30%时，钢球自由行程较大，受转速率影响也大，容易产生无规律偏析；而当钢球较多充填率较高φ为40%～45%时，钢球自由行程较小，受转速率影响也小，偏析程度轻。在本文模拟条件下，合适的充填率φ应该在40%～45%范围，同时也能减少转速率的变化对偏析造成的影响。(5) 钢球在轴向的偏析，在上述充填率和转速率区间是客观存在的。另外，钢球尺寸和配比会影响整体钢球的空隙率，进而影响钢球的自由行程，通过合理的级配能减少或抑制钢球的轴向偏析；矿浆流从给矿端向排矿端流动造成的压力差、球磨机安装坡度的精准、筒体衬板形状、端盖衬板形状[16]等因素也值得研究。

4 结 语

球磨机内钢球无论是在筒体径向还是轴向都存在偏析现象，导致钢球粉碎物料效果不理想，影响球磨机工作效率，而目前工业试验和工业生产要研究钢球径向和轴向偏析，摸索时间长，工作量大，很难调节操控。本文采用三维离散元PFC3D软件模拟了级配钢球在球磨机筒体径向和轴向的运动，既能跟踪计算每一个钢球的运动轨迹，又能跟踪级配钢球运动的整个过程，为有效解决钢球介质在筒体径向和轴向偏析的问题提供了便利，节省了大量的成本与时间，并对进一步要研究的问题提出了初步建议。