尾墩体型优化对消减南水北调典型渡槽水位波动的效果研究
2023-01-30李立群陈晓楠王松涛许新勇
李立群,陈晓楠,蒋 莉,王松涛,许新勇,4,5
(1.南水北调集团中线有限公司,北京 100038;2.华北水利水电大学水利学院,河南 郑州 450046;3.咸阳市水利水电规划勘测设计研究院,陕西 咸阳 712000;4.水资源高效利用与保障工程河南省协同创新中心,河南 郑州 450046;5.河南省水工结构安全工程技术研究中心,河南 郑州 450046)
0 引言
南水北调中线工程是优化我国水资源配置、促进经济社会可持续发展的重大战略性工程,截至目前,工程已平稳运行7年有余,随着调水工况及环境的日益复杂,工程运行期间出现了一些新的现象,如渡槽尾墩末端出现了呈对称分布的漩涡带,槽身段形成了周期性水位波动现象,现场观测最大波高可达1.2 m,对南水北调中线工程平稳输水存在一定的影响和隐患。因此,对渡槽过流的水力特性和尾墩体型优化对消减槽身水位波动的效果开展研究,可为中线工程平稳调度和安全运行提供借鉴,具有一定的实际工程意义。
近年来,在水工水力学的研究方面,基于计算流体力学理论的水流动力学数值模拟逐步成为重要的研究手段并取得了较好的研究成果。颜天佑[1]等针对湍河渡槽基础冲刷问题,建立计算流体力学数值模型,运用浅水方程、大涡模拟湍流模型和干湿交界面处理方法,对渡槽进行基础水力特性的流体力学数值模拟并对渡槽槽墩周围流态特征与流速及水深分布规律进行了分析,为河床防护设计提供了理论依据。吴正厚[2]等对不同形式渡槽渐变段水力特性进行CFD 数值模拟计算。针对实际工程中常见的渡槽形式,用流体动力学计算软件Fluent 进行CFD 数值模拟。通过分析,比对出更为适宜的渡槽渐变形式,为实际工程中渡槽的设计、施工、选材及后期维护提供技术支撑。何照青[3]等采用标准k-ε紊流模型,利用追踪自由水面的VOF法,对新疆北部小洼槽倒虹吸在不同流量下的三维流场进行了数值模拟,将模型与原型观测数据进行对比,模拟结果高度吻合;张曙光[4]为预测圆柱形桥墩周围的局部冲刷坑形态和最大冲坑深度,运用Flow-3D 软件的水动力学模块和泥沙输运模块对桥墩附近局部冲刷进行了三维数值模拟,验证了数值模拟冲刷形态及冲坑深度的可行性。吴佩峰等人[5]对采用戽流消能方式的下游河道水面波动情况进行研究,研究成果可以为大型工程防波设计提供参考依据。蔡芳[6]对于三维CFD 方法模拟调压室水位波动的准确性进行了计算,推动三维CFD 方法在计算漩涡和水位纵向振荡等问题的深入研究,获得了与实验数据高度吻合的结果。李大鸣[7]等人对于出山店水利枢纽工程齿坎式宽尾墩进行模拟,用Flow-3D 软件选取RNGk-ε湍流模型模拟水流形态取得和模型试验相近的效果。阿不都赛依迪·赛麦提[8]在对水库水位波动对土坝渗流的影响中发现,水位快速上升过程中,水位上升速率越大,对坡面破坏高度越高。
以往的研究中,主要是探究水位波动对建筑物的影响,在消除水位波动方面的研究相对较少,因此本文以南水北调中线某渡槽为研究对象,采用基于RNGk-ε模型和VOF 的计算流体力学方法,通过研究不同参数尾墩体型方案的水力特性,分析其水深、波幅等水力要素变化规律,探讨对波动消除的效果,以期为中线工程平稳输水和调度安全提供科学依据和工程参考。
1 计算流体力学方法与理论
1.1 水力控制方程
本次数值模拟的研究对象为水体的宏观流动,因此控制方程采用不可压缩黏性流体的连续性方程、动量方程、k-ε方程。其中,连续方程的表达式:
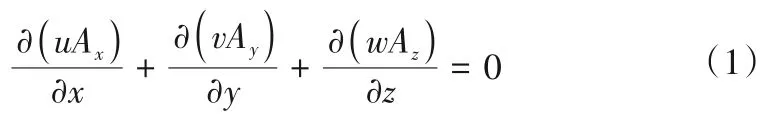
式中:u、v、w分别为x、y、z方向的流速分量;Ax、Ay、Az分别为x、y、z方向上可流动的面积分数。
动量方程的表达式:
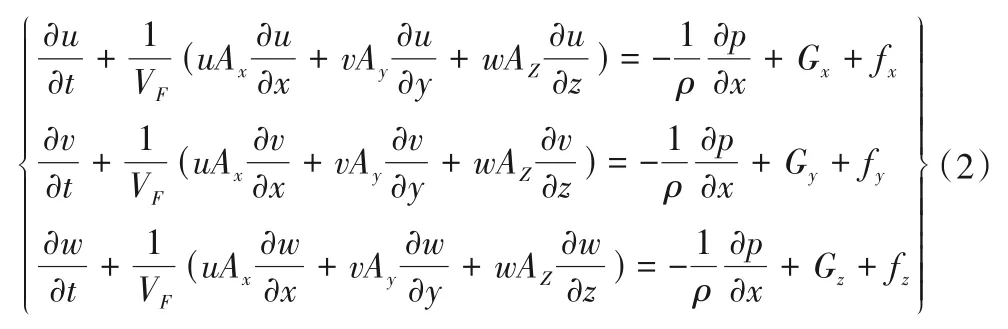
式中:Gx、Gy、Gz分别为x、y、z方向的重力加速度,m/s2;fx、fy、fz分别为x、y、z方向的黏滞力;VF为可流动的体积分数;ρ为流体密度,kg/m3;P为作用在流体微元上的压力。
湍动能k方程:
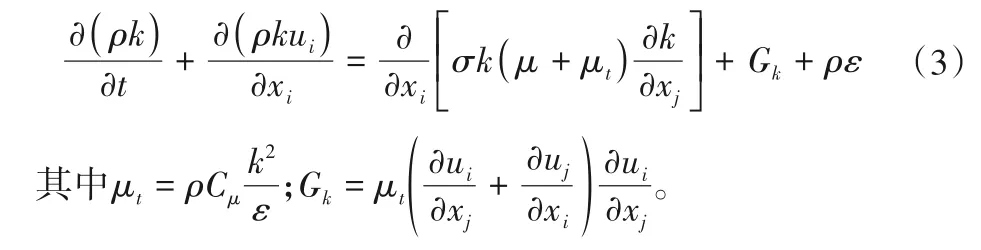
湍动能耗散率ε方程:
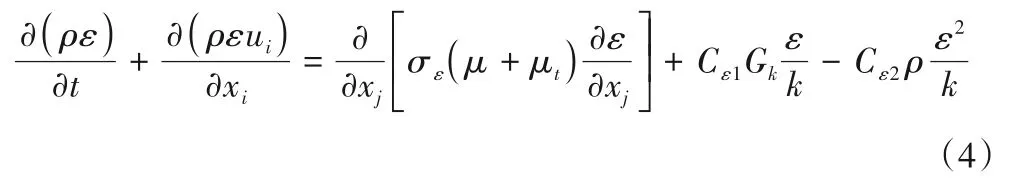
式中:μ为分子黏性系数;μt为紊流黏性系数;Cμ为经验系数;σk和σε为紊流普朗特数;Cε1和Cε2为方程常数;Gk为紊动能的产生项。
1.2 自由液面追踪的VOF方法
本次研究的重点是明渠流动及其自由液面的波动情况,因此,为更好地捕捉上述运动过程,采用VOF 法追踪模拟自由液面,其计算原理通过构造网格单元中流体体积和网格体积比的函数来追踪每个单元内流体的变化,并确定自由面[1]。在同一个单元中,水、气体或者两者的混合体具有相同的速度,即服从同一组动量方程,但它们的体积分数在整个流场中都作为单独变量。如果αω表示水的体积分数,αa表示气的体积分数,两者应满足以下关系:

在一个控制单元中,当:αω=1时,则说明该单元全部充满流体;αω=0 时,则说明该网格为空网格;0<αa<1 时,则说明该单元存在自由水面。
2 数值模型及现场实测数据
2.1 数值模型
以南水北调中线工程某典型渡槽为例,建立数值仿真模型,包括干渠与渡槽的连接段、闸室段、渡槽槽身,总长度261 m,宽度62 m,高度8 m。坐标X轴正方向为顺水流水平向,Y轴为与顺水流垂直向左,Z轴为与顺水流垂直向上。计算区域使用正六面体结构化网格进行划分,网格尺寸设置为0.5 m,对水力计算敏感的出口尾墩及下游渐变段加密处理,加密区网格尺寸设置为0.2 m,网格总数约94万单元,计算区域网格划分如图1所示。
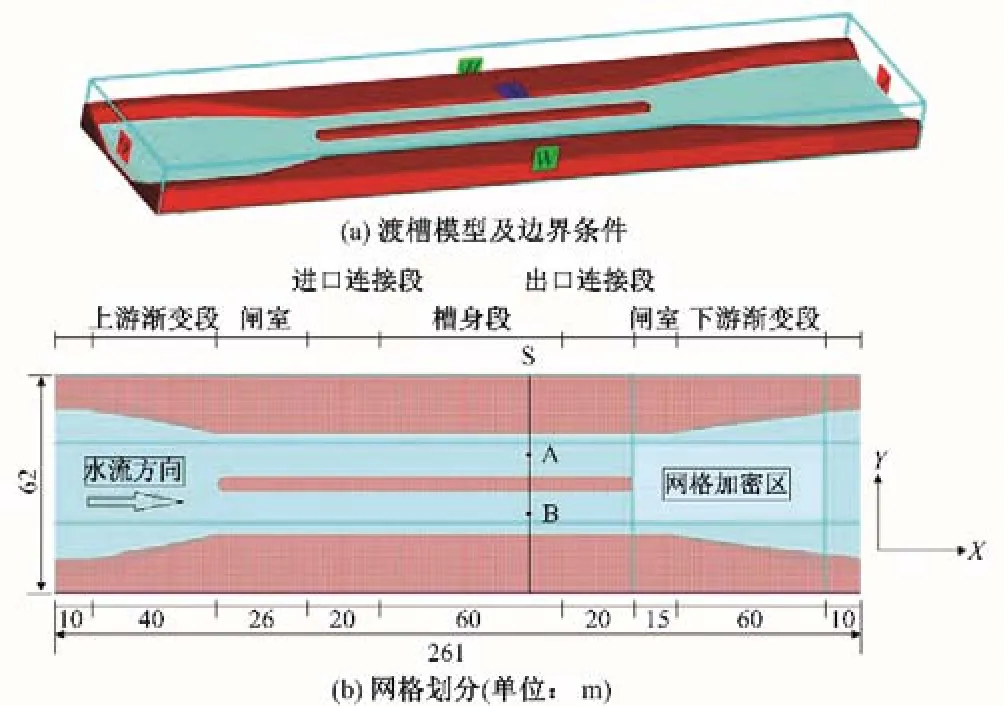
图1 网格划分示意图Fig.1 Grid division diagram
2.2 实时水情数据
瞬时流量为310.74 m³/s,进口水位141.70 m,水深6.45 m;出口水位141.59 m,水深6.34 m;上下游水位差为0.11 m。
2.3 实测水位波动数据
现场对S断面[距离下游连接段15 m 处,如图1(b)所示]进行多点测量,本次采用方形钢管连接旋桨流速仪进行水深、流速测量,现场作业如图2 所示。其中每个测点测量10 组数据,经过后期处理可得出左右断面中心点水位波动幅值最大,断面及测点分布如图1(b)所示。取顺水流为正方向,其中左断面中心A 点平均水深6.22 m,波动最大值0.56 m;右断面中心点B 平均水深6.23 m,波动最大值0.58 m;左右断面平均流速均为2.15 m/s。断面中心点实测水深变化曲线如图3所示。

图2 现场作业Fig.2 Field operation
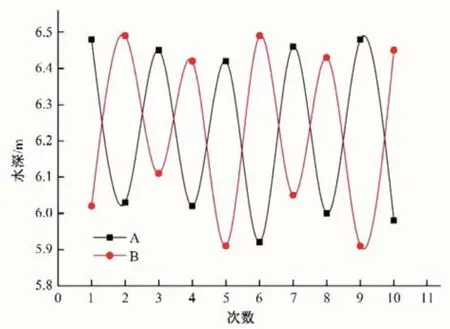
图3 左、右断面中心点实测水深变化曲线Fig.3 The measured water depth curve at the center of left and right section
2.4 计算参数及边界条件
数值计算选择边界条件为进口流量边界、出口流速边界(流量与水流断面面积比值可确定出口流速)、左右及底部为无滑固定边界。设置水体为不可压缩液体(One fluid,Free surface or sharp)。根据设计资料,水流黏滞系数设置为0.001 N·s/m2,渠道糙率设置为0.014,为消除初始条件影响,计算时间设置为1 800 s。
2.5 模型验证
将实测流量310.74 m3/s 作为本次模拟计算工况,根据现场实测结果选取断面波动最大点A、B进行计算验证。对S断面进行多点监测,发现同样为中点的B点比A点数据大,与实测结果保持一致,故选取B 点为研究对象进行模型验证。为了排除前期模型充水的影响,故选取400 s 之后的计算数据,B 点水深随计算时长变化曲线如图4所示,流速分布如图5所示。
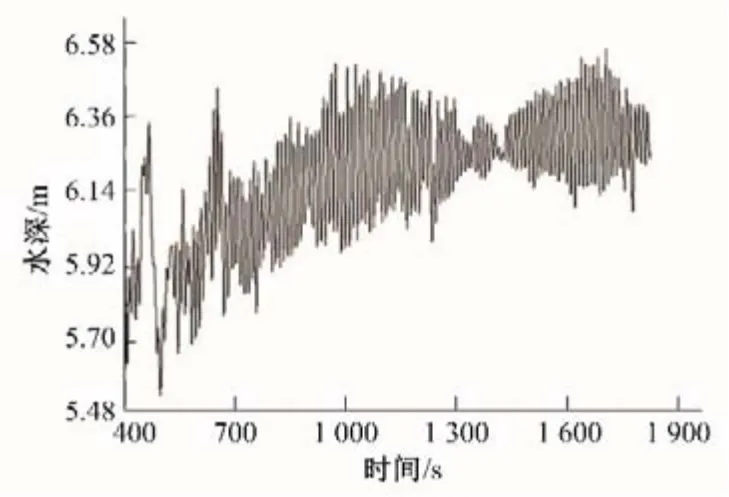
图4 水深随计算时长变化曲线Fig.4 Curve of water depth changing with calculation time

图5 流速分布图(单位:m/s)Fig.5 Velocity distribution contour
由图可知:前期水流较紊乱,随着计算时长的增加,波动逐渐趋于稳定,模拟计算波动最大值为0.54 m,与现场实测值0.58 m 相差7.4%;断面平均流速2.0 m/s,与现场实测值2.15 m/s相差7.5%;平均水深6.25 m,与现场实测6.23 m 相差3.17%,三者误差相对较小,表明数值模拟计算结果可信,方法可行。
3 计算方案及结果分析
3.1 计算参数及工况设定
计算模型、参数及边界条件设置见2.4 节,根据实测数据选取进口流量为340 m3/s,出口边界流速为1.255 m/s。对于渡槽出口出现的涡旋及槽身水位波动现象,较为常用的方法是在出口修建导流尾墩,但不同尾墩体型及结构尺寸效果差异较大,因此,本文将首先对常见尾墩体型进行研究,得到最适用于工程消波的体型后,再对该体型尾墩进行结构尺寸的详细探讨。所选尾墩体型见表1所示。

表1 不同尾墩体型工况Tab.1 Working conditions of different tail pier types
3.2 不同尾墩体型的消波措施效果对比
针对不同尾墩体型的消波措施效果研究,表2 给出了5 种工况随着不同墩体长度的波动控制效果,分别是在墩体长度在2.5、3、5、8、15 m 时渡槽内部水流的波动最大值。由表2(图6)可知,各工况波动幅值随尾墩长度变化的规律一致,波动幅值随着尾墩墩体长度增加逐步降低,渡槽内水流流态都得到了相应的改善,尤其以椭圆形尾墩的消波效果最佳。
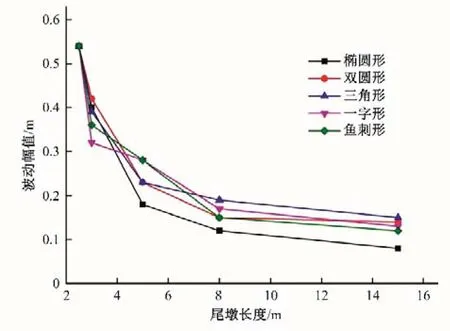
图6 不同尾墩型式长度与水位波动幅值比对曲线Fig.6 Comparison curves of different tail pier length and water level fluctuation amplitude
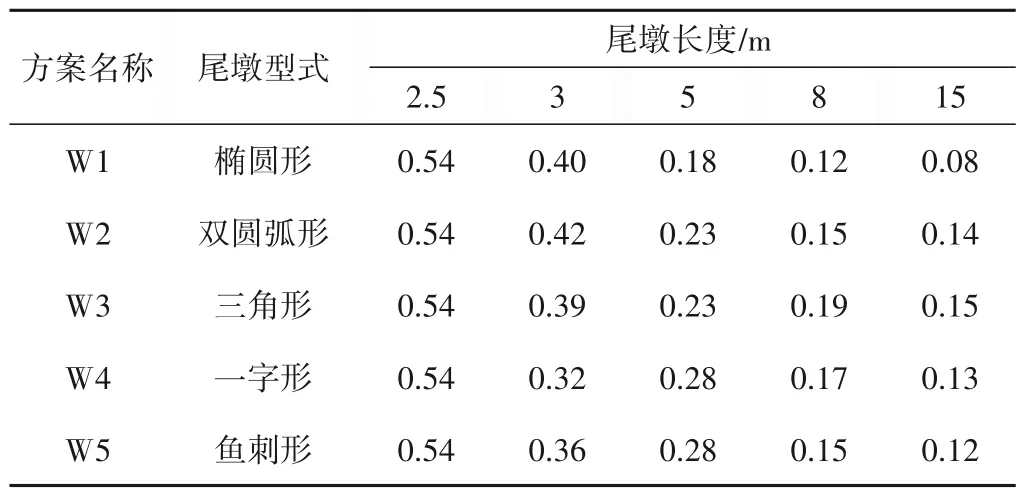
表2 尾墩长度与水位波动幅值比对Tab.2 Comparison of tail pier length and water level fluctuation amplitude
3.3 椭圆形尾墩消波效果分析
由3.2 节研究可知,诸多尾墩型式中,以椭圆形尾墩的消波控制效果最佳,对椭圆形尾墩消波的机理与效果进行深入研究,特按照上节椭圆形尾墩加长长度工况分别定为T0~T4,其中T0为工程现场原始尾墩。采用大流量输水时的水情数据,对椭圆形尾墩加长各个工况进行数值仿真计算,研究椭圆形尾墩长度对控制波动幅值的影响规律及效果。
3.3.1 槽身水深分布规律研究
图7 给出了渡槽水流1 800 s 稳定后,椭圆形尾墩各工况的渡槽槽身水深分布规律,由图7(a)可知,T0 工况(即原始尾墩)时,在渡槽左右两槽内,形成了波峰与波谷对称交替出现的水位波动现象,水位波幅较大,且周期性显著。随着尾墩墩体长度的增加,水位波动幅值逐渐下降,渡槽内水位逐渐趋于稳定,当加长长度超过8 m[图7(d)T3 工况]时,两槽内的波动现象基本消失,槽内水流流态逐渐平缓。
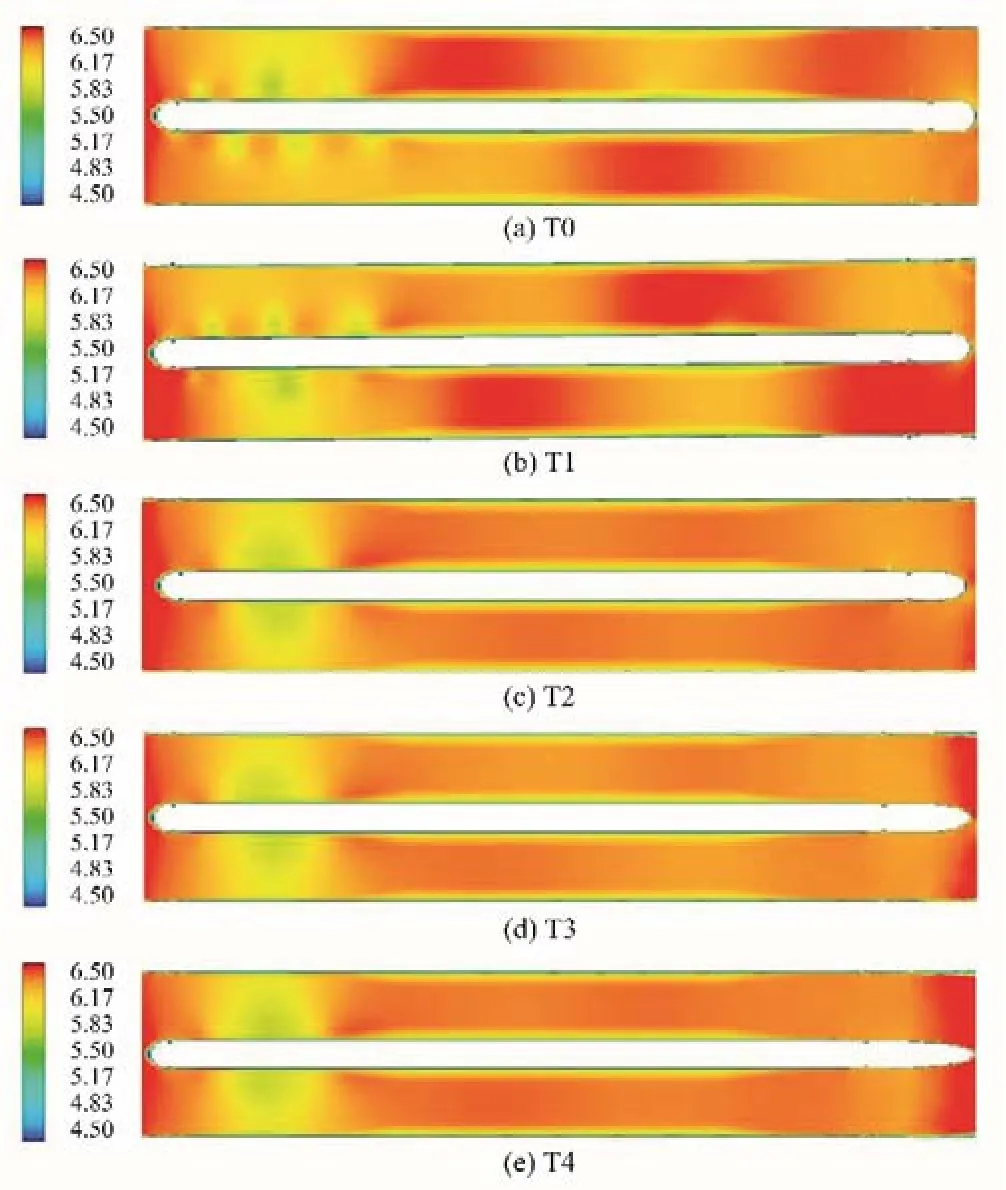
图7 椭圆形尾墩各工况水深分布规律(单位:m)Fig.7 Water depth distribution of elliptical tail pier under different conditions
3.3.2 椭圆尾墩波动幅值规律
对各工况波动幅值的变化规律详细分析,选取渡槽S 断面右侧槽身中间B点进行监测分析,因计算过程在400 s之前处于未稳定状态,故选取400~1 800 s 时间范围进行测点数据分析,监测结果见图8 所示。由图4 可知,在工况T0(即工程现状)情况下,测点波动幅值最大值达到了0.54 m,现场实测0.58 m。由图8(a)~(d)可见,随着墩体长度增加,波动幅值逐渐减小,T1、T2、T3、T4工况下波动幅值分别为0.40、0.18、0.12、0.08 m。
根据图8 各工况椭圆形尾墩的波动规律分析,图9 给出了模拟计算得到的墩体长度与其所达到的波动幅度控制效果之间的关系曲线。由图9可知,原始尾墩波动幅值达0.54 m,随着墩体加长,波动幅值迅速下降。当墩体长度达到8 m时,波动幅值降为0.12 m;在墩体长度进一步增加后,波动降幅趋于稳定,到墩体增长到20 m 时波动降幅也仅为0.08 m。可认为墩体长度加长能有效控制水位波动,但长度超过8 m 后,效果并不显著。
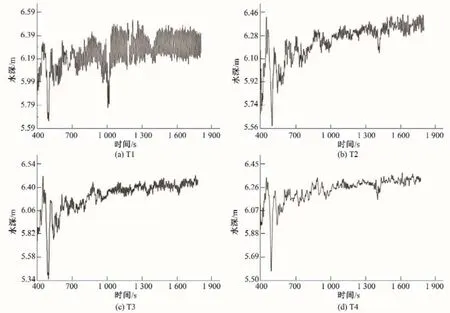
图8 椭圆形尾墩不同长度下的水位波动变化曲线Fig.8 Water level fluctuation curve of elliptic tail pier with different length

图9 随着墩体长度加长的波动取值曲线图Fig.9 Fluctuation value curve with length of pier
4 结论
通过计算流体力学对南水北调某渡槽的水位波动现象及控制措施进行了数值模拟,研究了不同尾墩体型及尾墩长度加长对波动的控制效果,可得以下结论。
(1)数值计算可模拟渡槽槽身内波峰与波谷对称交替出现的水位波动现象,工程常见的尾墩型式中,以椭圆形尾墩消波措施最佳;
(2)推荐椭圆形尾墩墩体加长工程措施时,随着尾墩墩体长度的加长,水位波动幅值逐渐下降,槽内水流流态逐渐平缓。但加长长度超过一定范围后,效果不再明显,推荐墩体长度采取8 m左右,可达到控制水位波动幅值和工程投资最优效果。
