考虑颗粒暴露角的宽级配泥沙起动流速公式研究

赵天龙，马廷森，付长静，3，岳 亮

（1.重庆交通大学 水工建筑物监测诊断技术重庆市高校工程研究中心，重庆 400074；2.青海省水利水电勘测规划设计研究院有限公司，青海 西宁 810001；3.南京水利科学研究院岩土工程研究所，江苏 南京 210029）

0 前言

堰塞坝溃决的细观过程是堰塞坝坝体颗粒在水流作用下的冲刷输移运动，本质上是非恒定漫坝水流与坝体非均匀土石料间的相互作用，属于泥沙运动的特殊形式。目前，对于泥沙运动，许多学者对不同情况下泥沙运动机理和影响因素进行了研究［1-7］，对不同条件下泥沙颗粒起动的数学表达式进行了推求［8-11］。对于水流作用下土石料的起动输移问题，多数集中于对河道泥沙颗粒运动规律的探索［12-15］，对于堰塞坝溃决时的土石料运动研究相对较少，堰塞坝土石料相较于河道泥沙颗粒具有更宽的级配，在堰塞坝溃决过程中，土石料起动和输移内在规律也有别于河道土石料泥沙颗粒的运动。

早期的非均匀沙起动规律研究方法是将均匀沙的起动规律运用到非均匀沙不同粒径中得到分组起动流速及输沙率等。如Gessler［16］、Engiazaroff［17］、Nece［18］等均依托均匀沙起动规律开展过非均匀沙不同粒径分组临界起动流速方面的研究工作。在分组粒径输沙率研究方面，Parker 等［19］考虑到表层泥沙直接在水流作用下与推移质进行交换，提出了无量纲参数泥沙起动判别条件，通过引入拣选系数计算不同粒径切应力，得到卵石推移质分组输沙率计算方法。近年来，在不连续非均匀泥沙起动输移研究方面，各国学者开始关注不同粒径泥沙之间的相互影响。Elhakeem 等［20］通过量纲分析、水槽试验及回归分析方法，引入考虑非均匀沙不同粒径相互影响的推移质挟沙密度函数，建立了可以考虑不同输沙强度阶段表层泥沙和底层泥沙相互作用的非均匀沙推移质输沙公式。孙志林等［21］建立了适用于河网的对数型非均匀沙挟沙能力公式，改进了一维河网输沙微分方程和离散计算模式。王洪虎等［22］通过水槽冲刷试验，分析了床沙和推移质的分形特征，并对不同床沙、不同流速条件下的泥沙粒度分维值进行了定量计算与对比。严军等［23］借助图像识别技术研究床面粗化对推移质输沙率和颗粒级配的影响。白玉川等［24］在精细模拟大颗粒泥沙间绕流作用的基础上，重点研究了非均匀大粒径泥沙随机排列所产生的垂向暴露度和纵向暴露度对起动的影响。

国内外学者从现场调查、理论分析和数理统计到模型试验，以及数学模型解析等不同角度，对泥沙颗粒输移运动规律进行深入的研究，取得许多宝贵的成果，而对于堰塞坝溃决过程中的土石料的运动输移规律仍鲜有学者开展专门研究，堰塞坝溃决从细观角度看，是堰塞坝土体在漫坝水流作用下的水沙相互作用及泥沙运动过程，这种水沙相互作用是在一定坡度宽级配土石堆积体上发生的。而直接将现有的河道泥沙运动理论套用到堰塞坝溃决计算中，所得结果与实际工况存在差别。因此，将泥沙运动力学与堰塞坝坝料及堰塞体特征相结合，对坝体溃决过程中的非均匀土石料颗粒起动流速进行分析具有实际工程意义。

1 颗粒暴露度分析

所谓的暴露度，指的是土石料的暴露度指土石料相对于河床表面的暴露程度。现有的暴露度理论在讨论土石料暴露程度的时候并不存在一个确定的基准面，多数学者在研究土石料的暴露程度时是以水平面作为基准面进行探讨，在具有一定坡度的河床上亦是如此。对于河床坡降较大或者粒径差别较大的堰塞坝溃决土石料的运动来说，这种假定过于粗糙。对于堰塞坝床底坡度较大的情况，其基准面应随河床坡度值的变化而发生变化。在本研究中假定颗粒暴露度的基准面为河床的平均床平面，暴露度是指土石料相较于该床平面的暴露程度。不同坡度的河床，其平均床平面坡度也不同，分析暴露度的基准面自然不同。鉴于此，提出土石料颗粒空间暴露度如图1所示。

图1 颗粒暴露角示意图Fig.1 Schematic diagram of particle exposure angle

如图1所示O1、O2、O3、O4为土石颗粒的重心，C、D、E为所研究颗粒O1与下层颗粒O2、O3、O4的接触点，B为所研究土石料颗粒的重心O1所在铅垂面和河床床平面的交线AB上的点，O1B垂直于AB。图1 中的横向暴露角和纵向暴露角在二维平面上的示意图如图2所示。

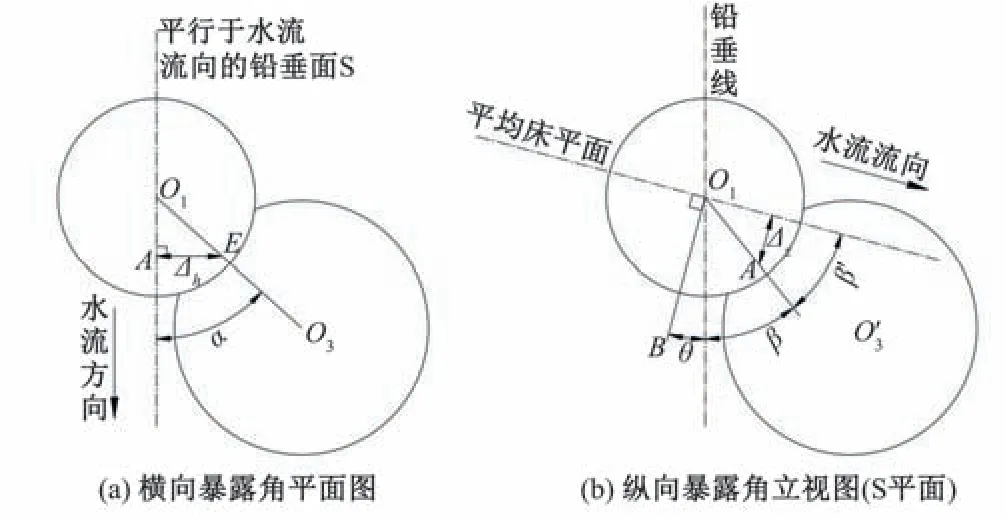
图2 泥沙颗粒横、纵暴露角示意图Fig.2 Schematic diagram of horizontal and vertical exposure angles of sediment particles

图2 中D、E为颗粒O1与下游两颗粒O2、O3的接触点，θ为河床平均床平面的坡度，α为过颗粒O1重心与DE垂直的线段O1A与颗粒O1、O3连线的夹角，称为土石料的横向暴露角，取值范围为［0°，90°］；β为O1A与铅垂方向的夹角，β+θ为纵向暴露角的余角，则纵向暴露角β'=90-β-θ，β'的取值范围为［0，90°］。当β'=90°时，从顺流向的铅垂面（S 平面）上分析泥沙颗粒处于完全暴露；当β'=0°时，泥沙颗粒处于完全隐蔽临界状态。

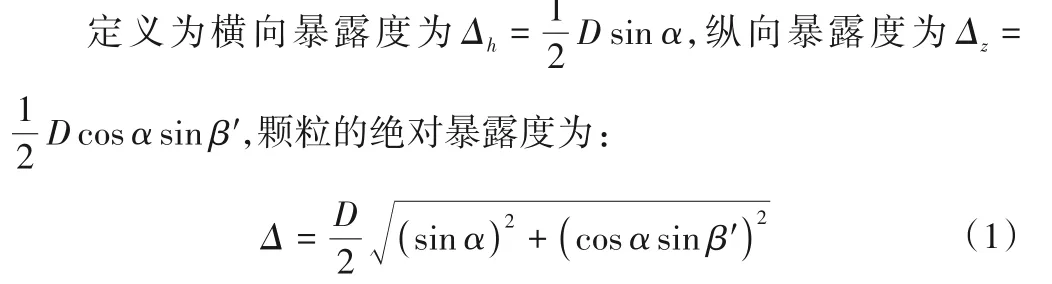
由式（1）可以看出，除了纵横向暴露角外，颗粒自身粒径对其绝对暴露度也有较大影响，暴露角相同时，绝对暴露度的值与颗粒粒径成正比，粒径越大，绝对暴露度的值也越大。韩其为［25］将颗粒的相对暴露度表示为颗粒绝对暴露度与颗粒自身粒径的比值，如式（2）所示，即：

这种表示方式侧重均匀沙的暴露度分析，在表现非均匀沙颗粒之间的遮蔽关系时略显不足。因此，本文将颗粒的相对暴露度定义为颗粒的绝对暴露度和与其紧邻接触的下游侧颗粒粒径D'的比值，用公式表示如下：

式（3）可表示不同粒径泥沙颗粒间的遮蔽作用。堰塞坝坝体颗粒为非均匀土石料，颗粒的粒径对暴露度有很大的影响。对于横、纵暴露角度数相同，但上下游颗粒粒径大小不一，相对暴露度也就不一样，相对暴露度与粒径成正比。取下游侧颗粒粒径D'=0.1 mm，横、纵暴露角度数为45°时，所研究颗粒粒径大小与下游颗粒粒径比值对暴露度的影响如图3。

图3 颗粒粒径比值与暴露度的关系图Fig.3 The relationship between particle size ratio and exposure

从图3 可以发现，颗粒粒径对其相对暴露度存在较为明显的尺寸效应影响。尤其对于堰塞体坝料等宽级配土石颗粒，颗粒之间的粒径差别将显著影响颗粒的暴露程度。当土石颗粒级配越窄时，影响暴露度的尺寸效应并不明显，而随着级配变宽，尺寸效应愈发明显。当颗粒的暴露角度不变时，上游颗粒粒径D较下游颗粒粒径D'小，相对暴露度值小，当下游侧土石料颗粒的粒径D'和所研究颗粒粒径D相等时，相对暴露度的值为1，上游颗粒粒径D较下游颗粒粒径D'大，相对暴露度值也随之变大。

取下游侧颗粒粒径D=0.1 mm，D'=0.1 mm，横、纵暴露角对暴露度的影响如图4。

从图4可以发现，随着颗粒的横纵向暴露角度数的增加，颗粒相对暴露度也呈现增大的趋势，但这种趋势随着暴露角度数的增加逐渐减缓。

图4 横、纵向暴露角与相对暴露度的关系图Fig.4 The relationship between horizontal and vertical exposure angles and relative exposure

图5 中D/D'取值最小为0.001，最大为1 000。该图表明，随着粒径的增加，颗粒的横纵向暴露角度数对相对暴露度的影响增大，对于同完全隐蔽临界状态下（α=0°，β'=0°）的颗粒，不管颗粒粒径怎么变化，颗粒的相对暴露度不变，值为零；对处于非完全隐蔽状态下的泥沙颗粒，随着颗粒粒径的变粗，颗粒的相对暴露度数值相应地增大。颗粒越暴露，粒径越粗，其相对暴露度取值也越大。此外，随着颗粒的横、纵向暴露角度数的增加，颗粒相对暴露度也呈现增大的趋势，但这种趋势随着暴露角度数的增加减缓。

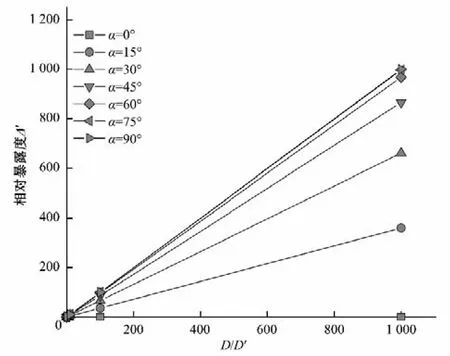
图5 粒径比值、暴露角与相对暴露度的关系Fig.5 The relationship between particle size ratio，exposure angle and relative exposure

2 颗粒起动流速计算

对不同条件下泥沙颗粒起动流速条件的研究，张广根［8，26-29］、孟震［30］等人进行了大量的研究。由于泥沙颗粒粒径大小不同，所对应的起动条件也有所不同，为此将泥沙颗粒的起动流速划分为细颗粒的起动条件和粗颗粒的起动条件分别进行推求，然后借鉴李林林［31］的研究思路，将推求得到的泥沙颗粒的瞬时起动流速转换为断面垂线平均流速，可得颗粒起动流速计算方法如下。

2.1 细颗粒起动瞬时流速

对于细土石料，所受的力［25，32，33］有：托曳力FD、上举力FL、重力G、黏着力Fμ、附加下压力ΔG。其中FD方向与水流方向一致，FL的方向与水流的方向垂直，黏着力Fμ、附加下压力ΔG、重力G方向铅垂向下，各个物理量的表达式如下。

式中：D为土石料颗粒的直径；uc为水流瞬时速度；ux为泥沙颗粒的运动速度；CD为水流的托曳力系数，取0.4；AD为托曳力面积作用系数，AD=π/4；CL为水流上举力系数，取0.1；AL为上举力面积作用系数，取值为，AL=π/4；ρ为水的密度；γs为土石料的容重；γ为水的容重；K2=2.258×10-3；δ1为薄膜水的厚度，取值为δ1=4×10-7；δ0一个水分子的厚度，取值为δ0=3×10-10；q0=1.3×109kg/m2；t为土石料之间的缝隙。当t＞δ1时，存在于各土石料颗粒周围的薄膜水相互不接触，此时Fμ、ΔG不存在。各力的力臂为：

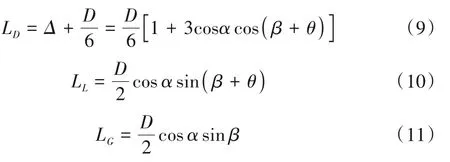
即设起动泥沙颗粒运动速度ux=0，运用滚动模型，以图6中的A点为滚动中心建立模型，力学表达式为：

图6 颗粒受力分析图Fig.6 Analysis diagram of particle force

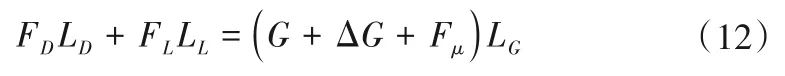
可推求得到细土石料起动的临界水流速度uc为：

从上述式子可以看出，颗粒粒径大小及河床床面坡度θ、横向暴露角α、纵向暴露角β'对泥沙颗粒起动存在影响。细粒径颗粒的起动流速由两部分组成，第一部分uc1由托曳力FD、上举力FL、重力G引起，uc1的大小与粒径D成正比，粒径越大，颗粒起动所需的水流流速也越大。与河床床面坡度θ有关，且与土石料颗粒在水中的横向暴露角α和纵向暴露角β'有关。第二部分uc2除托曳力FD、上举力FL外，还有颗粒与颗粒之间的黏聚力和附加下压力相关，uc2随着粒径的增大反而减小，与颗粒粒径的二次方成反比关系，与泥沙颗粒的横向暴露角α、纵向暴露角β'也相关。

2.2 粗颗粒起动瞬时流速

对于土石料中粒径较大的颗粒，认为附加下压力∆G与黏着力Fμ值为0，则可推求得出土石料起动的临界速度为：

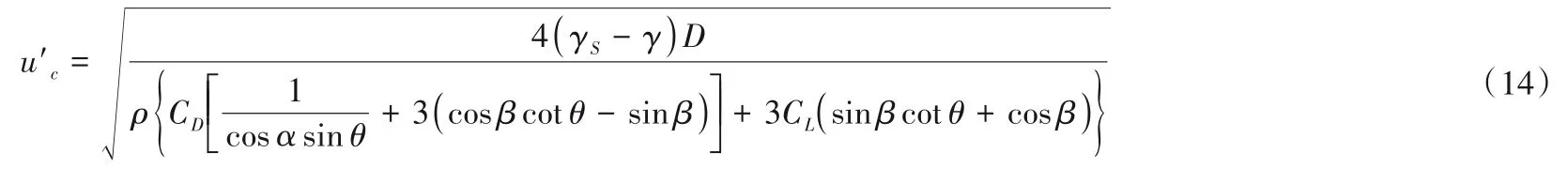
上式表明：土石料中粒径较大颗粒的临界起动流速与土石料颗粒的粒径D成正比，颗粒粒径越大，起动所需的水流流速也越大。还与颗粒所在的床面坡度θ有关，与土石料颗粒的横向暴露角α、纵向暴露角β'相关。

2.3 土石料起动的垂线平均流速

窦国仁认为瞬时流速uc与时均流速之间存在下述关系［33］：

依据窦国仁按照n的不同取值，对土石料的起动状态进行定义，n取1、2、3 分别代表床面土石料的起动状态为弱动、中动、普动。当土石料起动状态为弱动时，λ=1.37；中动时，λ=1.74；普动时，λ=2.11。

现有研究表明明渠近底时均流速与摩阻流速关系可表示为下式所示的对数分布关系［34］：

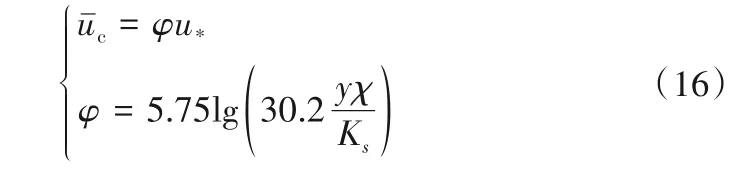
式中：u*表示处于床面位置水流的摩阻流速；y为水流近底流速作用点的位置，y=2D/3，χ=1，Ks=2D。

韩其为［25］认为垂线平均流速U和摩阻流速u*之间存在如下所示的指数关系，可表示为：

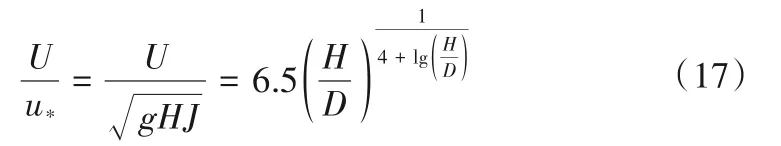
将式（15）、式（16）代入到式（17）中可得到土石料起动时的垂线平均流速的表达式为：

式中：

3 起动流速敏感性分析

3.1 公式验证

（1）均匀沙起动流速验证。利用现有的泥沙颗粒起动流速公式和国内外研究者的实测流速［31，33］对本文公式进行验证，对比验证所采用的公式如表1所示。

表1 各学者推求的起动流速表达式Tab.1 The starting flow velocity expressions deduced by various scholars

其中，泥沙颗粒的密度为2 650 kg/m3，水深为0.15 m。本文公式中床底坡度θ=0°，泥沙颗粒的暴露程度为α=0°，β'=0°，λ=1.74，粒径范围为0.001～1 000 mm，计算结果如图7所示。

由图7 可以看出，利用本文计算公式所得泥沙起动流速与实测结果相对较为吻合，但上述公式未考虑泥沙颗粒的暴露度对起动流速的影响，本文所求得的起动流速公式可在一定程度上反映出床底坡度和泥沙颗粒的暴露度对起动流速的影响。此外，根据本文计算公式，0.15 m 水深条件下，颗粒起动流速的分界粒径大致为0.1 mm，即当颗粒粒径大于0.1 mm 时，颗粒的临界起动流速随粒径的增大逐渐增加，而当颗粒粒径小于0.1 mm 时，颗粒起动呈现出相反的起动规律，即随着粒径的减小，颗粒临界起动流速逐渐增大。根据图7 可以看出，本文公式计算所得分界粒径略小于实测数据（0.17 mm），即当颗粒粒径小于分界粒径时，计算起动流速略小于实测值，分析原因是由于随着颗粒粒径的减小，颗粒间黏滞阻力与其自身惯性力相比逐渐增强，而该部分起动阻力并未体现在本文计算公式中。因此，对于细颗粒泥沙而言，利用本文公式计算所得起动流速数值相对偏小。

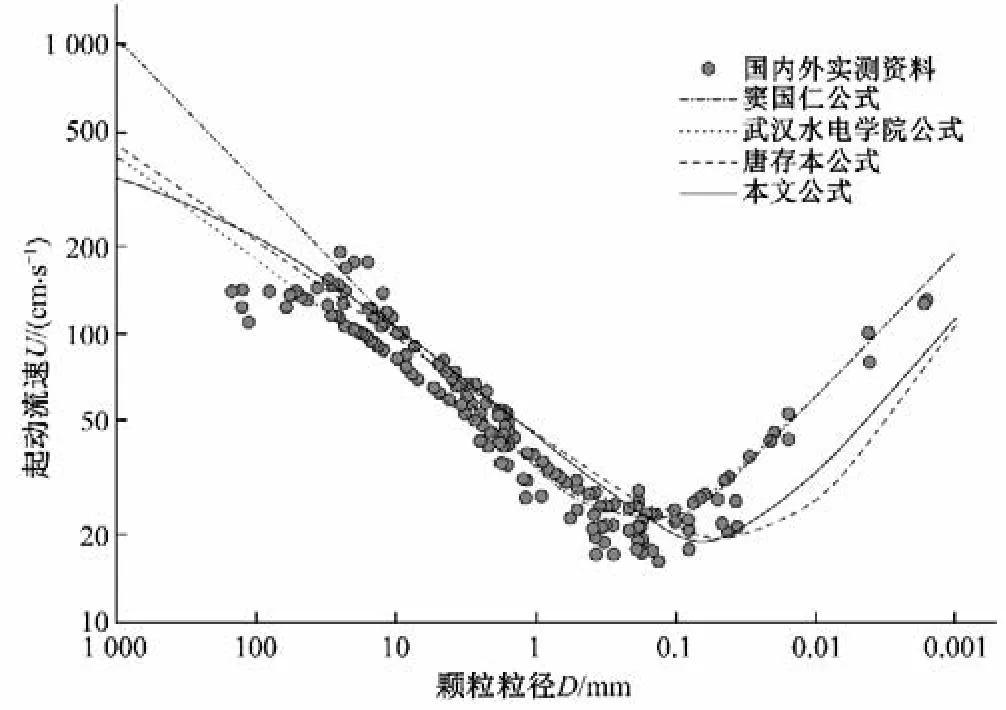
图7 均匀沙起动流速验证Fig.7 Verification of uniform sand incipient velocity

（2）非均匀沙起动流速验证。如前文所述，随着泥沙颗粒级配宽度的增加，大小粒径颗粒之间的遮蔽作用会愈加明显，颗粒暴露度对其起动流速的影响将更为显著。为此，选择非均匀沙实测资料来验证颗粒暴露度影响下的泥沙起动流速计算结果合理性。此处，选择本文公式、韩其为公式［25］［U=0.080 2f(λ)φ(Δ')ϕ并借鉴《泥沙起动规律及起动流速》［35］中所涉及到的长江寸滩水文站（1966）、万县水文站（1973）及宜昌水文站（1973）非均匀沙起动底速野外实测数据进行对比验证，计算结果如图8所示。

图8 非均匀沙起动流速验证Fig.8 Verification of incipient velocity of non-uniform sediment

由图8 可以看出，利用本文计算公式进行颗粒暴露度影响下的非均匀沙起动流速计算时，计算结果与实测结果在一定程度上较为接近，究其原因，主要由于进行非均匀沙计算时，大颗粒对小颗粒的阻挡、遮蔽，小颗粒对大颗粒的包围、填实作用对颗粒起动流速影响相对明显，将颗粒暴露度的影响考虑其中，起动流速计算结果将更趋于合理。

3.2 床面坡度对起动流速的影响

下面对床底坡度、泥沙颗粒横、纵向暴露度对起动流速的敏感性进行分析。堰塞坝溃决时漫坝水流流量大，其溃决过程从本质上讲是溃口土石材料被漫坝水流不断冲刷并被挟带至下游河道的过程。流速粒径之间的关系曲线如下所示，此时横向暴露角度数α=0°、纵向暴露角β'=90°，为泥沙颗粒完全隐蔽临界状态。β=90°-θ，水深为0.15 m，θ取不同值时粒径与起动流速的关系曲线如图9所示。

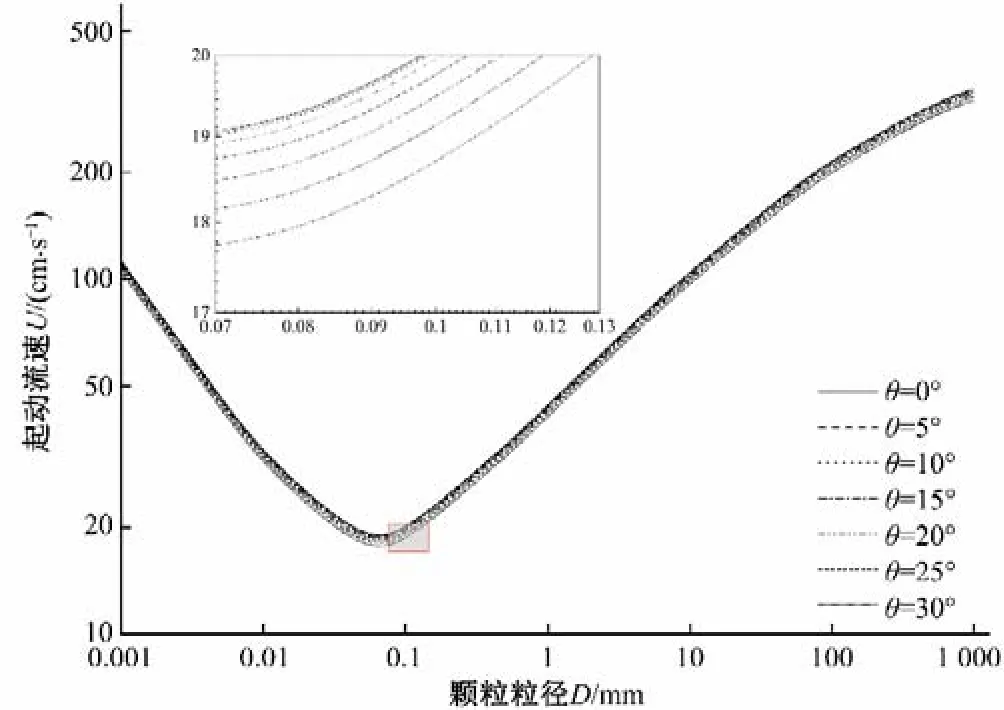
图9 颗粒完全隐蔽临界状态下底床坡度与起动流速关系曲线Fig.9 The relationship curve between the slope of the discharge channel and the starting velocity in the critical state of the particles being completely hidden

由图9可以看出，随着床底坡度的大幅增加，完全隐蔽状态下不同泥沙颗粒的起动流速所受影响较小，尽管底床坡度从0°增加到了30°，但泥沙颗粒的起动流速变化较小。由此表明，对于临界隐蔽状态下的泥沙颗粒，床面坡度对其影响较小。

一般认为床底泥沙颗粒的暴露度服从正态分布，床面泥沙颗粒暴露角均值为45°度。此处认为泥沙颗粒的横向暴露角度数为α=45°、纵向暴露角度为β'=45°时，为斜面上泥沙颗粒横纵暴露角的均值。在水深为0.15 m 时，床面坡度θ取不同值时粒径与起动流速的关系曲线如图10所示。

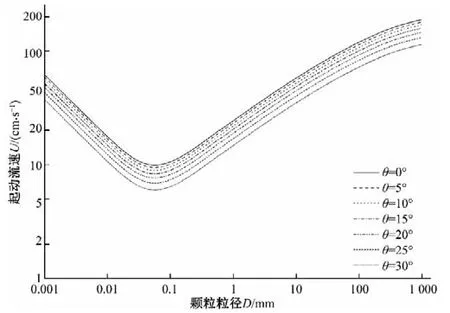
图10 暴露角均值状态下泄流槽坡度与起动流速关系曲线Fig.10 The relationship curve between the slope of the discharge channel and the starting velocity in the state of the average exposure angle

可以发现，随着床底坡度的大幅度增加，均值暴露角条件下不同泥沙颗粒的起动流速有较大的差别。对于粒径为1 mm的泥沙颗粒，当床面坡度从0°增加到了30°时，泥沙颗粒的起动流速从24.48 减小到14.81 cm/s，表明对横、纵暴露角处于床面暴露角均值的泥沙颗粒来说，床面斜坡倾角对土石料颗粒的起动流速有一定影响。随着床面坡度的增加，同一暴露程度下的泥沙颗粒的起动流速逐渐减小。

堰塞坝溃口底坡倾角越大时，泥沙颗粒起动流速就越小。当α=0°、β'=0°、β+θ=90°时，泥沙颗粒在完全隐蔽状态，当θ度数在0°到45°范围内增加时，上述力臂的表达式就可写为以下形式：

从上面3 个力臂计算公式可以看出，当颗粒处于隐蔽临界状态时，对于粗泥沙颗粒，上举力和托曳力力臂均为定值，仅重力力臂为变量。随泥沙颗粒所在床面的平均坡度θ增加时，β值减小，重力力臂LG相应减小，在相同暴露度条件下随着河床坡度的增加泥沙颗粒的起动流速逐渐减小。

3.3 颗粒暴露角对起动流速的影响

（1）横向暴露角α 对起动流速的影响。当纵向暴露角β'=0°，床面坡度θ=10°，泥沙颗粒粒径D=5 mm，水深H=0.15 m 时，横向暴露度α在0°～90°变化时，为泥沙颗粒隐蔽状态。横向暴露角α与起动流速曲线的关系曲线如图11所示。

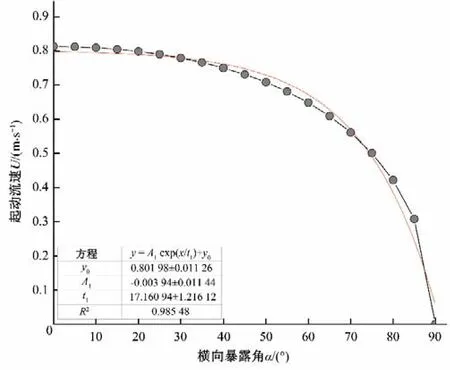
图11 颗粒横向暴露角α和起动流速关系曲线Fig.11 The relationship curve between the lateral exposure angle of particles and the starting flow rate

从图11 可以看出，随着泥沙颗粒横向暴露角度数增加，颗粒的暴露度增大，泥沙颗粒的起动流速与之呈现负相关关系，起动流速快速减小，且颗粒的起动流速与其横向暴露角α大致呈指数函数的关系。此外，从图11 可以看出，当颗粒的横向暴露角α为90°时，其起动流速趋近于零，分析原因是由于，当颗粒纵向暴露角为0°时，研究颗粒与其下游紧邻颗粒的重心连线平行于床平面，此时研究颗粒与其紧邻颗粒之间的空间位置取决于横向暴露角，而当横向暴露角α=90°时，研究颗粒与紧邻颗粒的重心连线垂直于水流流动方向，即研究颗粒的背水面临空，此时不考虑下游颗粒约束，处于倾斜床面的圆形颗粒在静水条件下即存在较高的起动概率。

（2）纵向暴露角β'对起动流速的影响。当横向暴露度α=0°，颗粒粒径D=5 mm，水深为0.15 m，床底坡度θ取不同的值，纵向暴露度β'在0°～90°之间变化时，纵向暴露角β'与起动流速的关系曲线如图12所示。

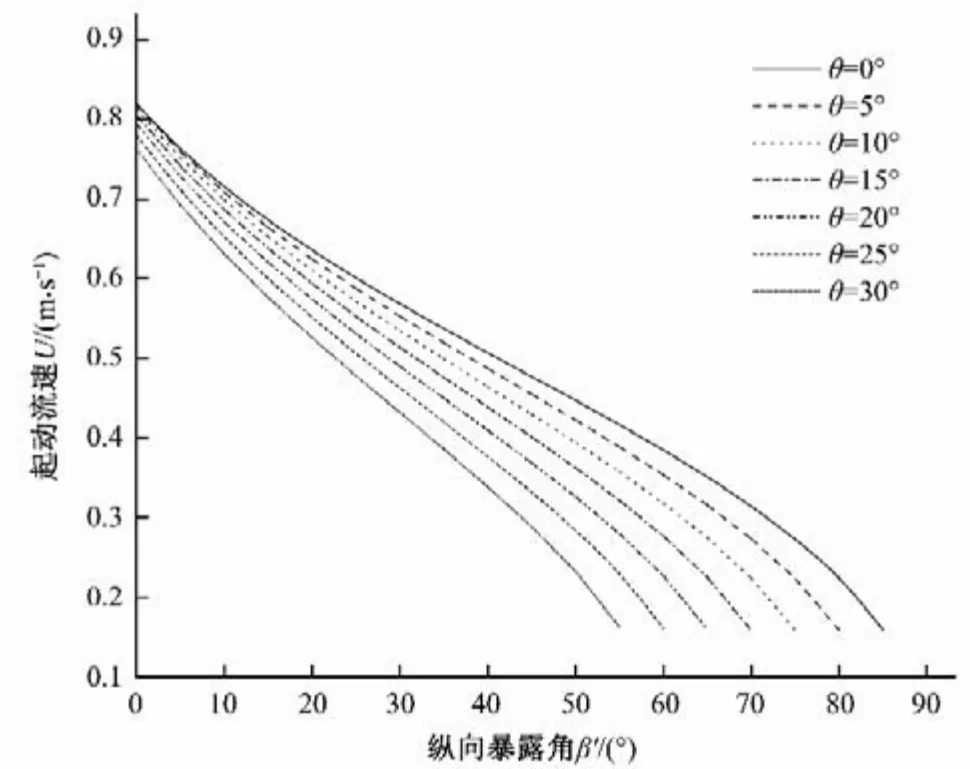
图12 颗粒纵向暴露角β′和起动流速关系曲Fig.12 The relationship between the longitudinal exposure angle of particles and the starting velocity

从图12中可以发现，随着泥沙颗粒纵向暴露角β'的度数增加，颗粒起动流速值减小，表明随着颗粒的纵向暴露程度增大，泥沙颗粒起动流速与纵向暴露角β'成反比，起动流速急剧减小。当纵向暴露角β'的度数一定时，随着床面坡度的增加，泥沙颗粒的起动流速减小，且起动流速的差别比较大。可以看出，坡面上的泥沙颗粒相较于平面更容易起动。

3.4 宽级配土石料临界起动流速分析

堰塞坝坝料级配范围宽，不均匀性强，有的堆积体还夹杂着巨石，直径从十几厘米到数米不等。因此，坝体遭受水流冲刷时不同位置不同颗粒的暴露度差异巨大。坝体溃口表面土石料颗粒相对暴露度不仅受其相对位置即颗粒横、纵向暴露角的影响，还受泥沙颗粒粒径大小的影响，具体表现为。

（1）颗粒相对位置一致，但两组颗粒的粒径存在明显的差别时，上游侧的泥沙颗粒粒径大于下游侧泥沙颗粒的粒径，即D/D'＞1，该工况下泥沙颗粒粒径对相对暴露度存在放大效应，使得泥沙颗粒相对暴露度数值上远远大于均匀颗粒间的相对暴露度。此时，泥沙颗粒受水流作用，决定其能否起动的主要因素是颗粒自身的粒径。依据图9 和图10 可以看出，相同的水深条件下，当床面坡度θ，颗粒的横向暴露角α，颗粒纵向暴露角β'一致时，颗粒粒径是颗粒起动流速的主控因素。

（2）颗粒相对位置一致，上游侧的泥沙颗粒粒径小于下游侧泥沙颗粒的粒径，即D/D'＜1，该工况下泥沙颗粒粒径对相对暴露度存在削减效应，使得泥沙颗粒相对暴露度远远小于均匀颗粒间的相对暴露度的取值。表现为粒径越小，相对暴露度越小，颗粒在床面越隐蔽。此时，泥沙颗粒受到水流的作用，由于下游侧大粒径泥沙颗粒的阻碍作用，使得颗粒较难起动。

（3）两组颗粒的粒径相同，但相对位置不同时，颗粒的横、纵暴露角对颗粒的起动有很大的影响。结合图4、5、11、12可以看出，随着颗粒暴露角度数的增加，颗粒的相对暴露度增大，暴露于床面，颗粒所需的起动流速变小，更容易进入运动状态。反之颗粒暴露角度数小，颗粒的相对暴露度较小，在床面上越隐蔽，颗粒所需要的起动流速变大，难以被水流带离床面发生起动。

4 结论

针对堰塞坝坝料不均匀性强、级配范围宽的特点，分析了泥沙颗粒的暴露度，并提出了可考虑泥沙颗粒暴露角的宽级配泥沙起动流速计算公式。取得的主要结论包括：

（1）通过引入横向暴露角和纵向暴露角，提出了适用于宽级配土石料颗粒的暴露度计算表达式，并以泥沙颗粒滚动模型为基础，建立了包含泥沙颗粒横、纵向暴露角以及底床坡度的泥沙颗粒起动流速公式，并选择现有计算方法及实测资料对本文计算公式进行了合理性验证，结果表明本文公式可在一定程度上较准确的反映含底床坡度及颗粒暴露角的泥沙起动规律。

（2）底床坡度与泥沙颗粒起动流速存在负相关关系，随着底床坡度不断增加，泥沙颗粒起动流速总体呈现逐渐减小的趋势，但影响程度受颗粒暴露程度影响明显，随着泥沙颗粒暴露程度不断增加，底床坡度对其起动流速影响逐渐增强。泥沙颗粒的横向及纵向暴露角与其起动流速呈现负相关关系，随着颗粒的横向暴露度增加起动流速不断减小。

（3）当被研究颗粒处于暴露状态时，忽略水力要素及周围水流结构作用，颗粒起动与否将主要受控于颗粒自身粒径影响，颗粒纵、横向暴露角对颗粒起动流速的影响规律存在差别，颗粒横向暴露角与起动流速成指数函数关系，随暴露角增加对起动流速的影响程度逐渐增加，颗粒的纵向暴露角与起动流速呈现S 曲线关系，随暴露角增加对起动流速的影响先减小后增加。

此外，堰塞坝溃口土石料组成十分复杂，颗粒形状、大小、密度、相对位置等千差万别，且作用于泥沙颗粒的溃口水流条件又具有紊动特性，这两方面决定了溃口泥沙起动具有随机性。要准确计算堰塞坝漫顶溃坝过程中溃口泥沙的起动输移，需针对堰塞坝溃口表层泥沙颗粒暴露度等相关参数的概化取值及起动计算方法开展研究，同时结合堰塞坝漫顶溃口流量过程，分析溃口底坡及侧壁的泥沙起动输移速率，进一步将宽级配黏性泥沙起动计算方法应用于堰塞坝漫顶溃坝过程中的溃口冲蚀及扩展计算中。