基于弹性降阶变换法求解一类可化为Legendre方程的微分方程初值问题
2023-01-30李顺初邵东凤付雪倩桂钦民
李顺初,邵东凤,范 林,刘 盼,付雪倩,桂钦民
(1.西华大学 理学院,四川 成都 610039;2.北京东润科石油技术股份有限公司,北京 10029)
对于非线性微分方程的求解,Bisso[1]提出了一种基于非线性因子分解的新方法来求解一类非线性常微分方程;李建祥等[2]总结了一些可用变量替换简化为易求解的一阶常微分方程与高阶微分方程的类型及其解法;Mohyud-Din等[3]提出了微分变换法;Ahmed等[4]介绍了一种基于积分函数的指数形式的变换求解二阶常微分方程(OLDEs)通解的新方法;杨荣霞等[5]给出了一类可以使用升阶法求解的二阶非线性微分方程.过往研究的求解非线性微分方程的方法有很多,可以看出求解非线性微分方程的方法是不断创新的.
在经济学中,Marshall[6]首次提出了需求弹性的概念,肖人俊等[7]得到了供需价格弹性公式.之后,Woods等[8]给出了弹性的数学表达式.弹性变换是导数在经济学中的一个重要应用,是微分学在经济分析中一种有效可行的方法[9],它广泛应用于无标度网络模型[10]、空中交通需求弹性评价方法的比较[11]、油藏[12-14]等领域.
目前已有作者尝试利用弹性变换法求解微分方程,但他们只是针对Laguerre方程[15]和Chebyshev方程[16]进行了研究.本文针对通过弹性降阶变换法可转化为Legendre方程初值问题的微分方程进行求解.首先,给出了弹性的定义及其相关性质;然后,利用弹性降阶变换法将一类三阶非线性常微分方程初值问题转化为Legendre方程初值问题进行求解,并总结了其求解步骤;最后,给出相应结论与进一步的认识.
1 预备知识
定义1 每一个函数y=f(x)关于其对应的自变量x均存在弹性,即当函数y=f(x)可微且f(x)≠0时,有
(1)
称η是函数y=f(x)关于x的弹性函数,称函数y=f(x)是弹性函数的原函数,而称η在某一定点x0处的值ηx0为函数y=f(x)在该点处关于x的弹性系数,弹性η表示因变量y对自变量x的相对变化率.
引理1(导数的弹性表示)若η是y的弹性函数,且η二阶可微,y三阶可微,当x≠0,y≠0时,则有[16]
(2)
(3)
(4)
(5)
称为弹性逆变换,其中x,y≠0.
引理3[17]Legendre方程
(1-x2)y″-2xy′+μy=0(-1 (6) 其中μ为参数. 当 μ=l(l+1),(l=0,1,2,…) (7) 时,Legendre方程的通解为 y=APl(x)+BQl(x), (8) 其中A、B为任意常数, (9) (10) Pl(x)是Legendre多项式;Ql(x)是第二类Legendre函数,在|x|=1有奇性. 定理1对于如下一类三阶非线性常微分方程的初值问题: (11) 其中λ为参数,x,z≠0.当μ=l(l+1)时,其特解为 (12) 其中 (13) (14) C=z0. (15) 证明对式(11)作微分变换, (16) 其中y是z的弹性函数.根据引理1,有 (17) (18) (19) 把式(17)~(19)代入式(11)中的三阶非线性常微分方程,则可将其关于z~x的三阶非线性常微分方程降阶为关于y~x的Legendre方程(6). 将式(17)、(18)带入式(11)的初值条件 (20) 则有 (21) 解得 (22) 因此,我们可将一类三阶非线性常微分方程初值问题转化为Legendre方程初值问题: (23) 由引理2可知,当对式(11)作微分变换时,原方程的解为: (24) 当μ=l(l+1)时,将方程(6)的通解(8)代入式(24),得方程的通解 (25) 将x=x0代入式(25)得 C=z0, (26) 由引理3可知,当μ=l(l+1)时,Legendre方程(6)的通解为式(8),将式(8)代入(23)的初值条件(22),有 (27) 根据克拉默法则可求得 (28) (29) 将A、B、C的值带入式(25),即可求得初值问题的特解,证毕. 微分变换(16)被称为z~x的方程初值问题的弹性降阶变换,利用导数的弹性表示(17)、(18)、(19)将其降阶为低一阶的y~x的常微分方程初值问题,若降阶后的微分方程可解,则原微分方程初值问题可解.这种通过弹性降阶变换而获得微分方程初值问题解的方法,称之为弹性降阶变换法. 通过定理1及其证明可知,如果要求解的三阶非线性微分方程不易求解,那么可以通过弹性降阶变换法将其初值问题转化为二阶微分方程初值问题,若此二阶微分方程可解,则原三阶非线性微分方程初值问题可解. 根据定理1的证明,易得出弹性降阶变换法求解可化为Legendre方程的一类三阶非线性常微分方程初值问题的步骤,如表1所示. 通过以上求解步骤,给出了基于弹性降阶变换法求解可化为Legendre方程的一类三阶非线性常微分方程初值问题的流程图(图1): 图1 基于弹性降阶变换法求解可化为Legendre方程的一类三阶非线性常微分方程初值问题的流程图 例求解如下一类三阶非线性常微分方程的初值问题: (31) 其中x,z≠0. 解: 步骤1:所要求解的方程(31)是方程(11)的类型. 步骤2:对(31)作弹性降阶变换(16),则可将其关于z~x的一类三阶非线性微分方程的初值问题转化为关于y~x的Legendre方程的初值问题: (32) 步骤3:根据引理3,则可求得(32)中Legendre方程的通解为 (33) 其中 P0(x)=1, (34) (35) (36) C3=1, (37) A=1, (38) (39) 步骤6: 将A,B,C3的值带入原方程的通解(36),即可求得初值问题(31)的解: (40) 1)弹性降阶变换法可将一类三阶非线性常微分方程初值问题转化为Legendre方程初值问题,再根据Legendre方程通解对其进行求解. 2)本研究的目的主要是通过弹性降阶变换法,实现微分方程快速、简便地求解,进而求得其初值问题的解. 3)弹性降阶变换法不限于求解可转化为Legendre方程的非线性常微分方程初值问题,只要转化后的微分方程可解,则原微分方程初值问题可解. 4)弹性降阶变换法创新性地将经济学中的弹性作为一种工具引入到微分方程求解中,不仅扩大了方程的可解类,而且对于微分方程初值问题的求解提供了新思路.2 弹性降阶变换法及可化为Legendre方程的一类三阶非线性常微分方程初值问题
2.1 主要定理及其证明
3.2 弹性降阶变换法求解可化为Legendre方程初值问题的一类三阶非线性常微分方程初值问题的步骤
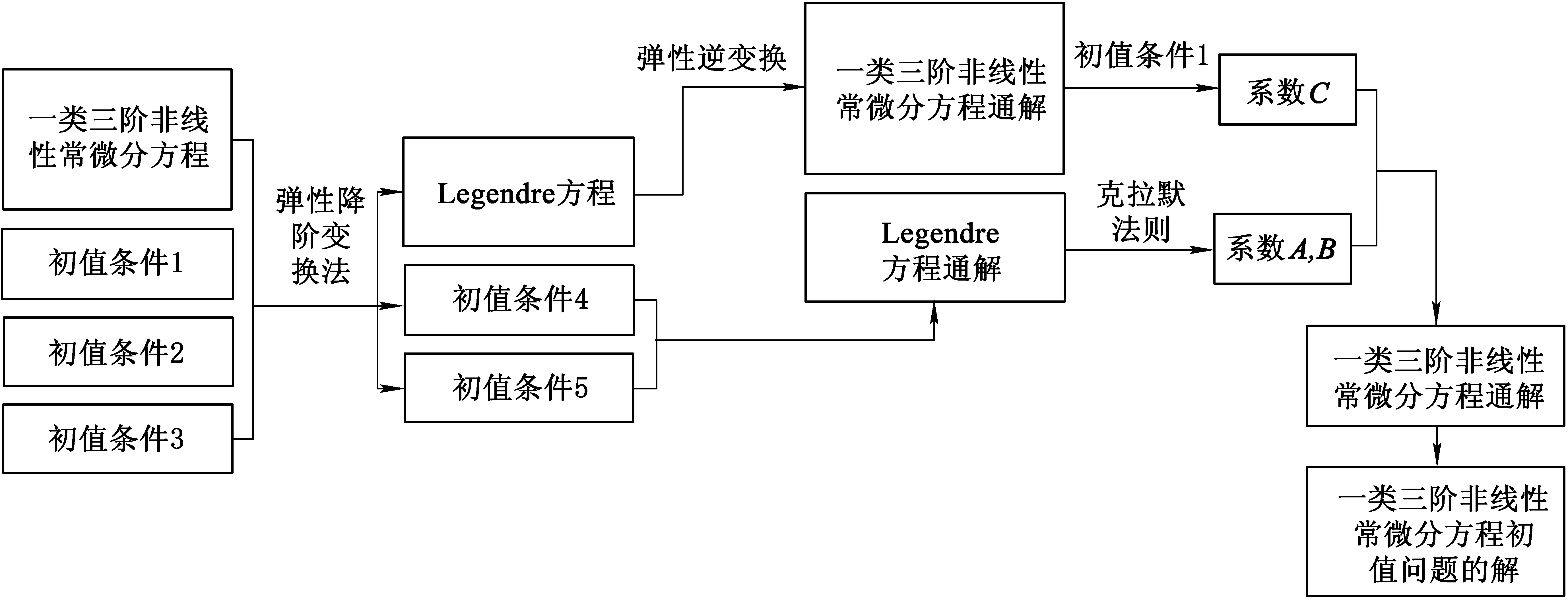
3.3 举例
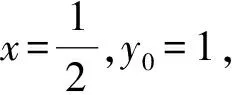
4 结论
