多层包铁结构超声反射频谱数值仿真

陈祎婷，陆铭慧，朱 颖，黄嘉诚，安仕伟，程树云，刘 洋

(南昌航空大学 无损检测教育部重点实验室，江西 南昌 330063)

0 引言

目前，在航空、航天、军工领域，薄壁多层结构复合材料因材料轻，形态可塑及功能完备，因而得到了广泛的应用。常见的多层材料可分为金属/金属、金属/非金属及非金属/非金属3类，超声检测是对各类多层复合材料适用性最广的检测方法。为了研究这种多层材料的质量检测问题，研究者们提出了超声频谱学。在研究连续和不连续介质的超声能量、散射衍射现象和多层介质中声波传播规律中不断总结归纳声波在多层介质中的反射与透射理论，为后续研究者们奠定了基础[4]。张建生[6]提出层滤波器原理，对钢层下橡胶粘接界面脱粘超声检测的原理和信号处理技术进行了研究。Fredrik Hägglund等[7]提出了一种线性方程组，为多薄层结构的脉冲反射法和透射法进行了建模，并且提出了利用模型中一种参数估计多薄层结构采用的各材料的声速、密度的方法。Jian Chen等[9]利用理论反射谱和实测反射谱，通过测得的试块厚度和反演算法推算密度、声速和衰减系数。Xiaoyu Yang等[10]将基于粒子群优化的最小二乘法运用于声压反射系数谱，同时对多层材料的多参量进行估算。郑善朴等[11]利用COMSOL软件对超声检测复合材料壳体/橡胶绝热层/橡胶衬层3层粘接结构的脉冲反射时域回波进行了仿真。高翔等[12]将时间反转和逆时偏移混合法用于层状介质中目标检测和定位的声场分析。

本文研究了一种新型的多层粘接复合材料，这种材料用于高海拔地区、具有加热除冰功能的直升机桨叶包铁结构上。与以往研究的多层复合材料相比，这种包铁结构层数多，介质多，层厚薄，需要识别的类型多[16]。声学上包铁结构的物理性质复杂之处是该结构属于上层高波阻抗低衰减、下层低波阻抗高衰减特性。难点是超声检测上层脱粘缺陷、加热元件、下层脱粘缺陷及无缺陷无加热元件4种典型类型时声波会产生严重的混叠，各类型特征区别微小且易掩盖。因此，需要研究对包铁结构具有针对性的超声检测方法。本文借鉴前人的多层结构反射谱模型，针对包铁结构和材料的特性对传统的超声反射频谱模型做了改进和参数修正，测试了包铁结构各材料的声学参量，建立了包铁结构的超声反射谱的模型，增加探头频谱参量，对水浸超声检测平板包铁试块的反射谱进行了仿真和实际实验，仿真结果与实际实验结果相符，结果表明该仿真模型可对实际检测技术起到较好的指导作用。

1 多层超声反射频谱模型

图 1为声波在薄壁多层材料中的传播示意图。图中，Wfm为入射声波，P0为入射波在零层的反射波，Pij为声波在第i层经过m次反射的声波。超声波直入射进入薄壁多层结构材料中，每层都会产生不同程度的反复反射和透射，这些声波叠加在一起使得最终接收的声波呈现出不同程度的混叠现象。设多层结构是线性时不变因果系统，各层介质均一稳定，整个过程可理解为是不同时段声波的时域卷积。多层结构超声信号时域的线性卷积模型、频域模型和Z域模型分别为

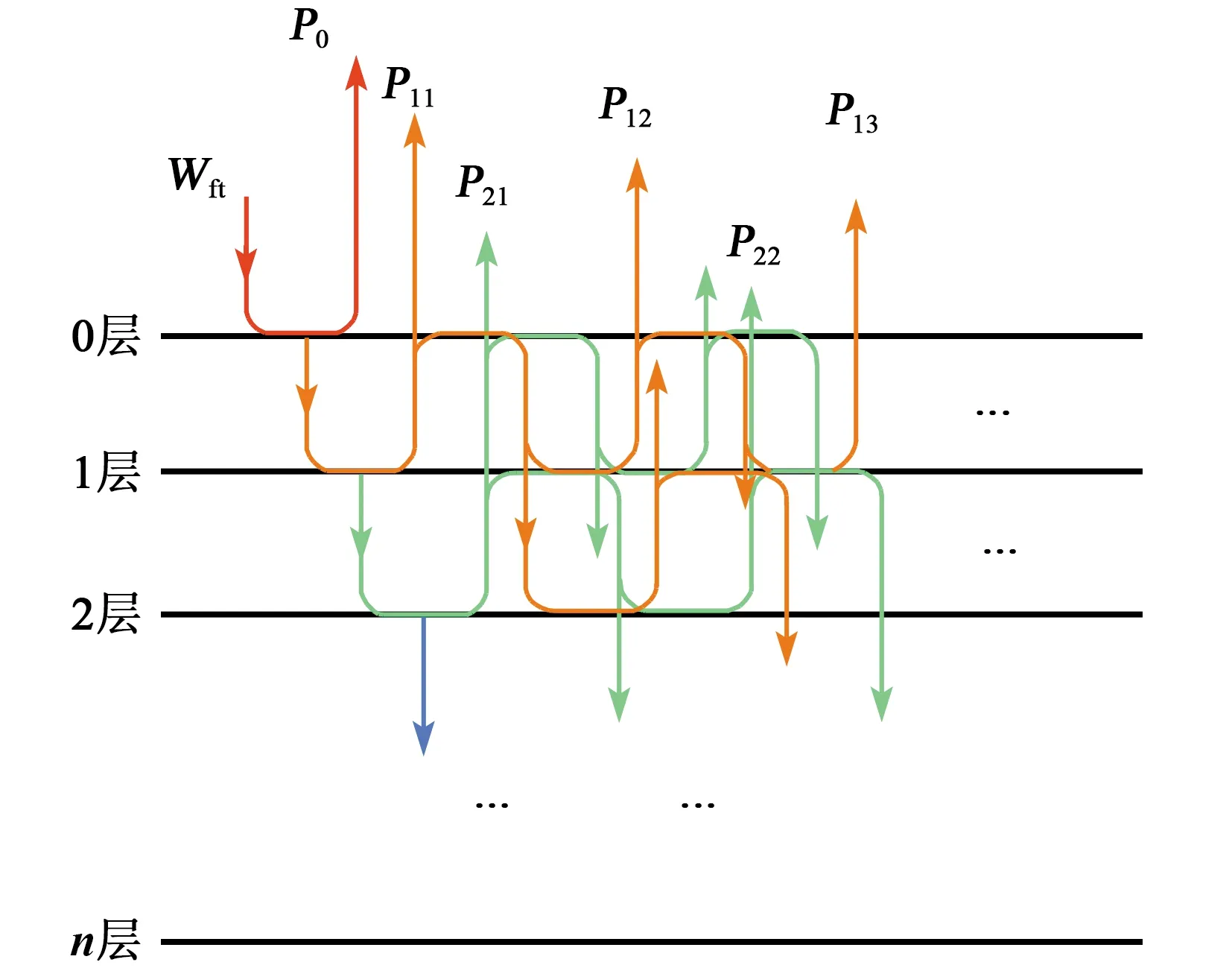
图1 声波在薄壁多层材料中的传播示意图

X(t)=W(t)*U(t)+N(t)

(1)

X(ω)=W(ω)U(ω)+N(ω)

(2)

X(z)=W(z)U(z)+N(z)

(3)

式中：*表示卷积运算；X(t)，X(w)，X(z)为多介质薄层结构的超声回波信号；W(t)，W(w)，W(z)为检测系统波；U(t)，U(w)，U(z)为多层结构的作用函数;N(t)，N(w)，N(z)为系统噪声;t表示时域;ω表示频域;z=ejω表示Z域。

首先分析声波在单层中的频域特征，以图1中第一层示意图为例，图2 为声波在单薄层中传播模型。

图2 声波在单薄层中传播模型

单层中经过1次、2次、3次反射的声波为

(4)

(5)

(6)

总结规律得出的声波在单层中经过k次反射的回波：

(7)

声波在单层中多次反射叠加的传播模型：

X(z)=p1+p2+…+pn+…=

(8)

A1=t01t10r12

(9)

(10)

(11)

(12)

式中：pn(n=1,2,…,k,…)为经过n次反射的声波；tij为从i界面进入j界面的透射率；rij为从i界面进入j界面的反射率；Zi为i介质声阻抗；α1为衰减系数；d1为1层厚度；c1为1层介质声速。

由式(8)可知，声波在单层薄层介质中传播的频域特性由为异界面声能分配作用的界面影响因素A1、入射声波的延迟因素z-2d1/c1、入射声波的衰减因素z-(2α1d1)及层对入射声波的频域响应因素Gω(z)决定。假设声波经过无穷次反射，则层频率响应因素如式(12)所示。

声波在多层结构中传播规律由不同单层对声波的作用组合一起形成。从声波的输入输出角度看，各层对声波的作用有3种形态，如图3所示。

图3 单层对声波的作用

(13)

(14)

(15)

式中:R(n-1)(n-1)(z)为从第n-1层输入第n层，经过第n层反射回到第n-1层的声波；T(n-1)(n+1)(z)为从第n-1层输入第n层，经过第n层透射进入第n+1层的声波；T(n+1)(n-1)为从第n+1层输入第n层，经过第n层透射进入第n-1层的声波。

令入射声波为1，式(13)～(15)分别对应图3(a)～(c)声波输入第n层再输出的3种情况。将多介质薄层分解成这些模块组合起来可构建出声波在多层结构中的反射频谱模型。

2 实验材料声学参量测试

2.1 实验试块

实验使用了一块仿照直升机旋翼包铁结构设计的200 mm×100 mm平板试块，该试块由不锈钢、橡胶、玻纤3种材料组成，结构由钢层(0.5 mm)、橡胶层(0.63 mm)、加热元件层(0.1 mm)、橡胶层(0.86 mm)、橡胶层(0.44 mm)、玻纤层(1.5 mm)粘接组成，用粘接层间不涂抹胶液来模拟脱粘缺陷情况，共制作3处人工缺陷：

1) 在钢层和橡胶层间制作一块30 mm×30 mm的上层缺陷。

2) 在橡胶层和玻纤层间制作一块40 mm×38 mm的下层缺陷区域。

3) 在1处上层缺陷下方制作一块40 mm×19 mm的下层缺陷，部分位置与上层缺陷重叠。

图4为试块设计示意图。为了研究3种介质材料的特性，利用生产余留的材料制作了一块不锈钢试块(尺寸200 mm×25 mm×1.96 mm)、橡胶试块(尺寸226 mm×46 mm×1.76 mm)和玻纤材料试块(尺寸130 mm×50 mm×4.96 mm)(长宽取最大尺寸)，3种试块的厚度均较薄，接近包铁结构中各材料层厚度。另外使用了一块DL-1不锈钢标准试块，试块实物如图5所示。

图4 平板包铁结构示意图

图5 试块实物

2.2 试块材料声学参量测试

如图6所示，利用超声发射接收仪、示波器、笔记本电脑搭建一个超声检测实验装置，以测试包铁各介质材料的声学参量。使用的超声检测探头有1.25 MHz 探头、2.25 MHz探头、5 MHz、10 MHz探头和15 MHz探头，耦合剂采用医用耦合剂。采集到的信号经过小波降噪后计算声学参量。

图6 声学参量测试实验装置及实验用探头

2.2.1 声速测试

测量了不锈钢、橡胶、玻纤试块的厚度如表1所示。用检测信号的前4组相邻底波计算，取平均值作为材料的声速：

表1 不锈钢、橡胶、玻纤试块厚度与材料声速

(16)

式中:tn为第n次底波时间定位点；tn+1为第n+1次底波时间定位点；d为材料厚度；c为材料声速。

2.2.2 声阻抗

用电子秤测量试块的质量，采用浮力法测量试块体积，计算材料密度，如表2所示。i材料声阻抗为

表2 试块参数

Zi=ρici

(17)

式中：ρi为i材料密度；ci为i材料速度。

2.2.3 频率-衰减系数曲线

由于橡胶和玻纤对高频信号衰减严重，测算频谱-衰减系数曲线使用的检测信号如表3所示。衰减系数为

表3 测算频谱-衰减系数曲线使用的检测信号

(18)

式中：P(n)-f0为第n次频谱中心频率波幅；P(n+k)-f0为第n+k次频谱中心频率波幅;αf0为f0处衰减系数。

每个信号用多对波段计算取中位数作为最终的衰减系数。图7为线性插值法拟合的频率-衰减系数曲线。

图7 线性插值法拟合的频率-衰减系数曲线

3 包铁结构超声反射频谱仿真实验

3.1 包铁结构超声反射频谱仿真

包铁试块的超声反射频谱建模主要考虑上层缺陷、加热元件、下层缺陷和无缺陷无加热元件4种信号。根据张建生[6]提出的传统模型对包铁结构超声反射频谱建模，4种信号经过各层的状态如表4所示。查阅文献[18]采用的声学参量如表5所示。仿真的包铁结构反射谱如图8所示。

表4 传统模型超声检测信号经过4类包铁结构各层时的状态

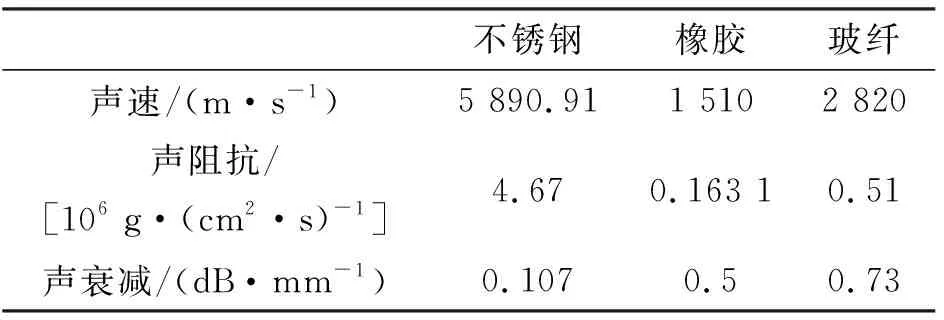
表5 传统模型使用的声学参量

图8 传统模型仿真的包铁结构的超声反射谱

本文对传统模型进行了结构改进和参数修正，新模型采用实测的声速、声阻抗数值，将传统模型中单一声衰减系数参数修正为频率-声衰减系数，根据材料声学参量测试的结果构造层的频率响应因素，表6为包铁结构超声反射频谱中4种类型信号经过各层的状态。图9为4种类型信号传播的简易示意图。

表6 经过4类包铁结构各层时新模型超声检测信号的状态

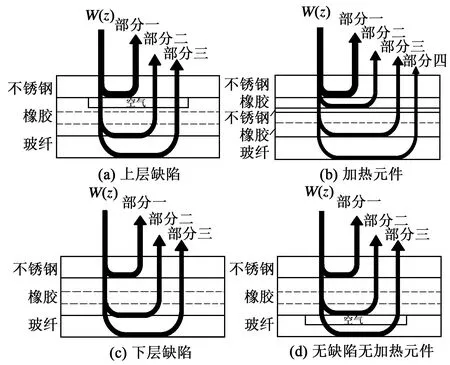
图9 4种类型信号传播的简易示意图

如图10所示，以无缺陷无加热元件类型为例，详述了该情况的包铁试块结构超声反射频谱模型。无缺陷无加热元件的声波反射频谱由仅经过钢层的声波频谱、从钢层上透射入橡胶层再返回的声波频谱及经过钢层、橡胶层透射入玻纤层再返回的声波频谱3部分构成。3部分相叠加构成了完整的模型：

图10 声波在无缺陷无加热元件结构中传播示意图

(19)

部分一：

A1=twstswrsr

(20)

(21)

(22)

部分二：

A2=twstsrrrgtrstsw

(23)

(24)

(25)

部分三：

A3=twrtsrtrgrgwtgrtrstsw

(26)

(27)

(28)

(29)

式中：tij为从i材料进入j材料的透射率；rij为从i材料进入j材料的反射率；di为i材料的厚度；ci为i材料的声速；αi为i材料的衰减系数；下标w、s、r、g分别表示水、不锈钢、橡胶、玻纤。另外3种类型的模型以此类推。令W(z)=1,不考虑声波输入系统的影响，图11为仿真的超声反射谱。图12为仿真超声反射谱的放大图。

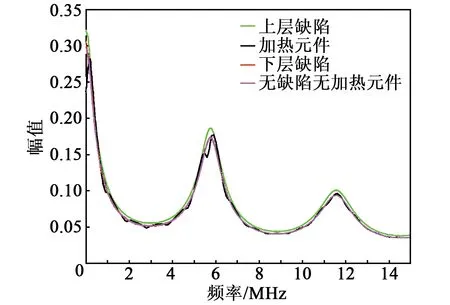
图11 新模型仿真的包铁结构的超声反射谱

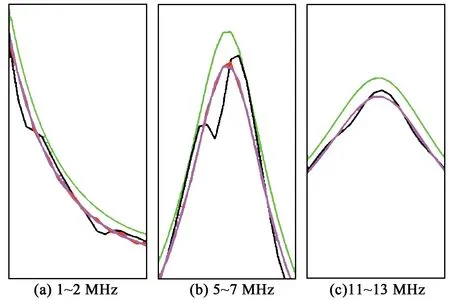
图12 仿真超声反射谱的放大图

传统模型和新模型在5～7 MHz和11～13 MHz处均出现波包，波包处各类信号差异较明显，传统模型中上层缺陷、下层缺陷波形相近，11～13 MHz处上层缺陷、下层缺陷和加热元件波形相近。新模型超声反射频谱是一个有波峰起伏的下行曲线，上层缺陷、加热元件两类较易区分，下层缺陷和无缺陷无加热元件波形相近，在低频范围内略有区别，11～13 MHz处波形几乎完全重合。

3.2 超声探头频谱测试

根据仿真的包铁结构声波反射频谱特性，选择2.25 MHz及5 MHz水浸聚焦探头作为检测探头。检测时为了更易检出下层缺陷，使探头声波聚焦至橡胶与玻纤界面处，采集此时接收的界面波频谱，则可得透射入试块的声波频谱：

(30)

式中：Z1为材料1声阻抗；Z2为材料2声阻抗；Wft为透射入试块的声波频谱；Wfr为从试块上反射后探头接收的界面波频谱。图13为探头透射入试块的声波频谱。

图13 探头透射入试块的声波频谱

3.3 实际超声检测包铁结构反射频谱仿真

将探头的声波频谱和包铁结构的超声反射频谱相乘，得到实际包铁结构超声反射频谱的仿真。图14为2.25 MHz和5 MHz探头检测包铁试块时声波通过4种类型结构的传统模型仿真反射谱。图15为2.25 MHz和5 MHz探头检测包铁试块时声波通过4种类型结构的新模型仿真反射谱。对比图14(a)、(b)可看出，2.25 MHz探头和5 MHz 探头均有可能分辨包铁4类结构，但2.25 MHz 探头效果更好。对比图15(a)、(b)可看出，上层缺陷和加热元件频谱曲线均易分辨，2.25 MHz探头检测的下层缺陷和无缺陷无加热元件频谱曲线在波峰处上下波动，5 MHz探头检测的下层缺陷和无缺陷无加热元件频谱曲线几乎重合。根据新模型推测使用2.25 MHz 探头分辨这4类结构的效果较优，5 MHz探头无法区分下层缺陷和无缺陷无加热元件这两种类型。

图14 2.25 MHz、5 MHz探头的检测信号的传统模型频谱仿真

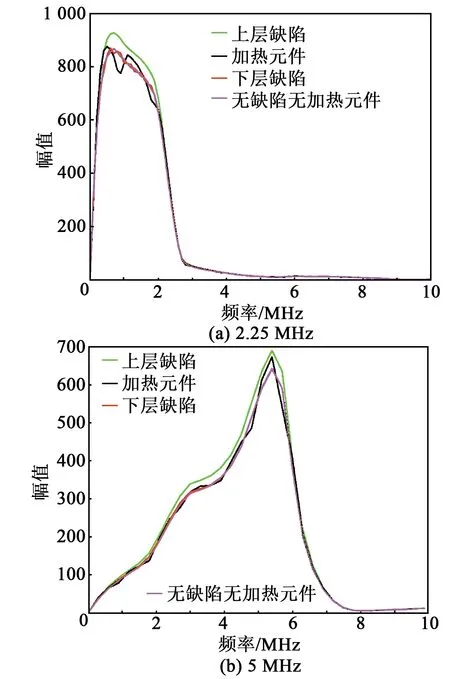
图15 5 MHz探头的检测信号的新模型频谱仿真

4 包铁结构超声反射频谱检测实验

使用2.25 MHz探头和5 MHz探头进行水浸超声反射法特征扫描，检测时调整探头高度，使声波聚焦在橡胶层和玻纤层之间，图16为超声特征扫描设备与探头。图17分别为2.25 MHz探头和5 MHz探头检测信号的频谱波幅层析成像。

图16 超声特征扫描设备与探头

图17 2.25 MHz、5 MHz探头检测包铁试块的频谱层析成像

图18分别为2.25 MHz探头和5 MHz探头的检测信号的实际频谱。成像图的明暗亮度对应的是幅值高低，成像效果与信号频谱曲线的表现基本一致。对比传统模型仿真结果与实际检测效果，传统模型仿真的5 MHz探头检测效果与实际差异较大，传统模型仿真结果显示5 MHz探头检测时4种类型可识别但互相之间差异较小，可实际检测时上层缺陷与3种差异明显，下层缺陷无法识别。对比图15(a)与图18(a)、图15(b)与图18(b)可知，新模型仿真的频谱曲线图和实际的频谱曲线图在频谱曲线的整体形态上有差异，但在中心频率、对各类型结构的表征等方面表现出较好的一致性。结合频谱曲线和成像图，2.25 MHz探头检测包铁试块可识别出下层缺陷，但5 MHz探头无法识别下层缺陷，证实了新模型仿真实验的结论。与传统模型对比，新模型对包铁结构超声反射谱仿真的结果更贴近实际检测情况，因此新模型比传统模型更适合包铁结构。

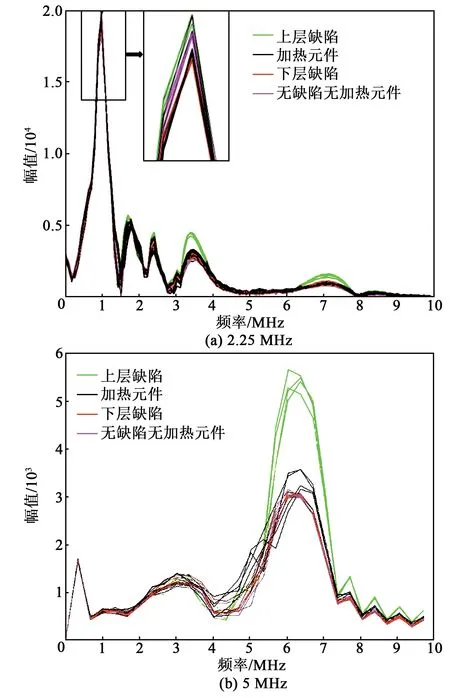
图18 2.25 MHz、5 MHz探头的检测信号的实际频谱

5 结论

1) 本文分析了多层结构的超声反射谱模型，首先建立了超声波在单薄层介质中的反射频谱模型，该模型由声波系统输入、延迟、衰减、界面、层频率响应等因素决定，在Z域中以各因素相乘构成完整的单层反射频谱模型。然后讨论了声波在单层中3种输入输出方向的反射频谱模型，将这两者结合可对多层结构的超声反射谱进行建模。

2) 制作了直升机机翼包铁结构平板试块和不锈钢、橡胶、玻纤材料试块，设计实验测试了这3种材料的声速、声阻抗、频率-衰减系数曲线。

3) 针对包铁结构的上层缺陷、加热元件、下层缺陷、无缺陷无加热元件4类情况构建了超声反射频谱新模型，引入探头频谱参量，用传统模型和新模型仿真了使用2.25 MHz探头和5 MHz探头实验的超声反射频谱，分析对比了4种类型的频谱曲线，推测2.25 MHz探头检测效果较优。

4) 利用水浸式超声特征扫描设备对平板包铁试块进行扫查，实验使用2.25 MHz探头和5 MHz探头对检测的频域信号做层析成像，得到了超声检测频域成像图。选取上层缺陷、加热元件、下层缺陷、无缺陷无加热元件4种类型点做超声反射频谱曲线，对比实际的检测效果与包铁结构的传统模型和新模型的仿真效果，新模型的仿真结果与实际实验结果更相符，证明了本文提出的包铁结构超声反射谱模型指导实际实验的可行性。