激光陀螺抖动轴失准角对陀螺精度的影响

李 鹏，王慧敏

(北京航天时代激光导航技术有限责任公司，北京 100094)

0 引言

二频机抖陀螺敏感轴名义上与抖动轴重合，实际上粘接的环节使两者很难严格重合，即抖动轴和敏感轴之间存在失准角(以下简称抖动轴失准角)。抖动轴失准角使与安装基座固连的陀螺坐标系各坐标轴不再是环形谐振腔的惯量主轴，抖动轮工作时，根据刚体欧拉动力学方程，将产生垂直于抖动轴的交变力矩，使抖动轴带动陀螺敏感轴横侧向同频摆动，形成单表级圆锥误差。此误差无法通过常规的圆锥补偿算法进行补偿,对于巡航武器、潜艇、飞机导航等应用场合，陀螺精度要求在导航级以上(优于0.01 (°)/h)[1]，需用技术手段对抖动轴失准角进行控制，这就需要一种可工程应用的抖动轴失准角测试方法。Geng LI等[2]提出一种实用的陀螺抖动轴失准角测试方法，但数据处理方法中抖动轴失准角结果存在与抖动轴初始安装角相关的误差。文献[3]指出，抖动轴失准角在惯性敏感器组件圆锥运动时产生误差。Kwangjin Kim等[4]指出抖动轴的横侧向偏移会带来误差。但均未给出与抖动轴失准角相关的动力学模型，以及抖动轴失准角对陀螺精度的影响。王林[5]推导了激光陀螺抖动的刚体动力学模型，但未对抖动失准角的影响进行分析计算。本文对激光陀螺抖动轴失准角的测量方法进行了优化，基于刚体对任意轴的转动惯量计算方法及欧拉动力学方程，分析了抖动轴失准角对激光陀螺精度的影响，提出在高精度的应用场合，抖动轴失准角应小于5′。

1 激光陀螺抖动轴失准角的测量

二频机抖式激光陀螺环形谐振腔与金属衬套胶粘后安装在抖动轮上，抖动轮安装在基座上。抖动轮基本结构及陀螺腔体安装方式如图 1所示。图1中标识出4个衬套安装钉，其余4个螺钉将抖动轮安装在基座上。

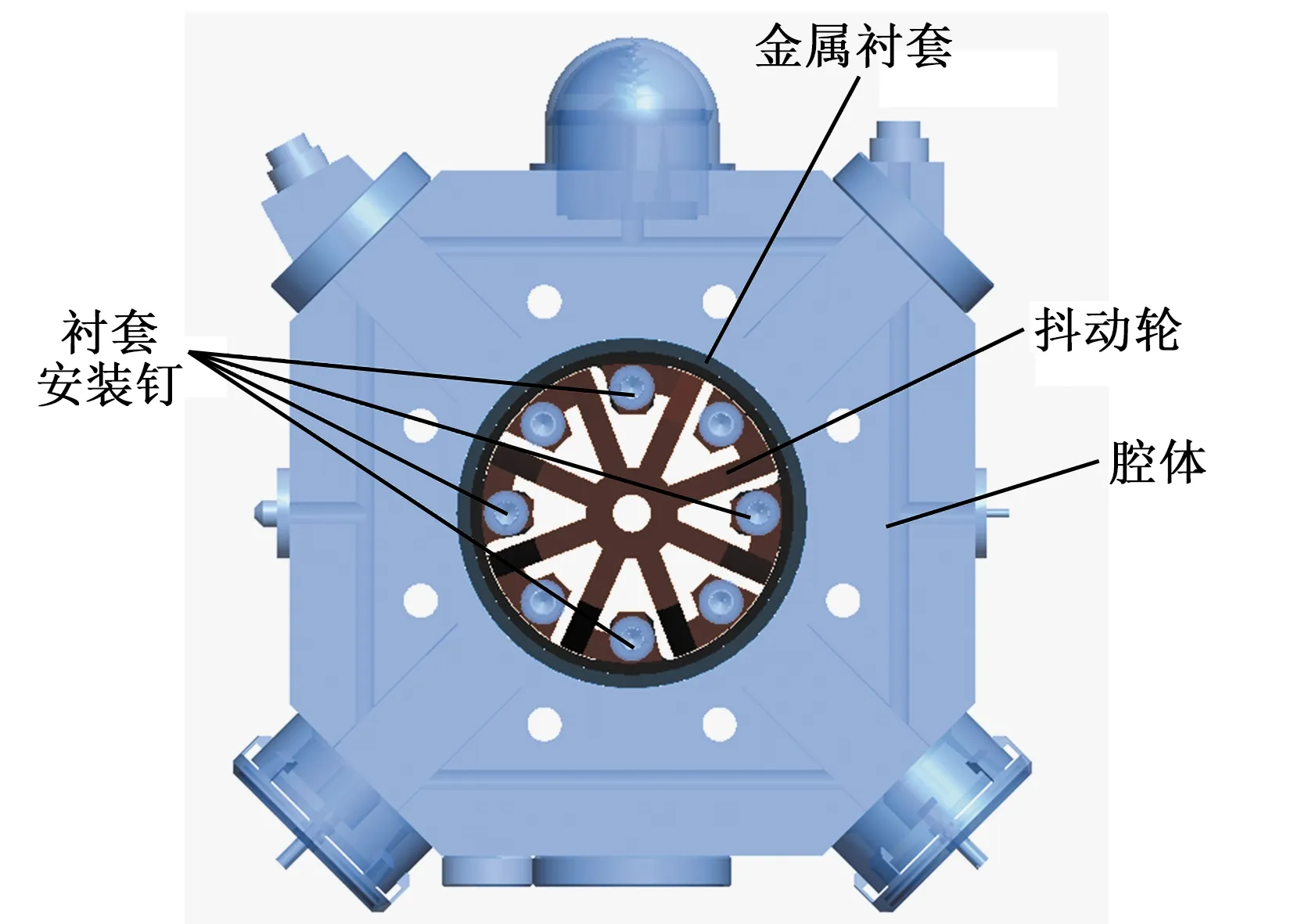
图1 激光陀螺抖动轮结构及安装示意图

建立坐标系O-XYZ如图2所示，OX与安装基准面垂直，OZ指向陀螺阴极，OY指向陀螺阳极一侧，并与另外两轴满足右手定则。DI为抖动轴，IA为陀螺敏感轴，垂直于闭合光路等效平面。a为抖动轴和陀螺敏感轴之间的失准角，b0为抖动轴相对X轴的基础偏角，为常值。陀螺抖动时，IA在绕DI的锥面上运动。

图2 抖动轴失准角示意图

将陀螺安装在单轴角振动台上(见图3)，振动台转轴与Z轴同向，角振动台振动角速率ωz=Acos(Ωzt),激光陀螺抖动角速率ωd=Bcos(Ωdt),当角振动台振动时，激光陀螺的输入轴IA将以抖动轴DI为转动轴做圆锥摆动(见图2)，则激光陀螺的输入角速率为

图3 抖动轴失准角测试方法安装示意图

(1)

式中b为陀螺输入轴与X轴的夹角在XOZ平面的投影，且：

b=b0+acos(Ωdt+θ0)

(2)

将式(2)及ωd代入式(1)，并利用小角的三角函数近似后可得陀螺输入的频谱分析结果[3]：

ωi=Ab0cos(Ωzt)+Bcos(Ωdt)+

cos[(Ωz-Ωd)t+θ0]

(3)

(4)

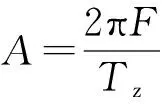
(5)

2 激光陀螺动力学建模

图4为典型的激光陀螺捷联惯组惯性敏感器本体结构，建立惯性敏感器组件本体坐标系O-XsYsZs，X陀螺坐标系O-gxxgxygxz。其中gxx垂直于陀螺安装基准面指向本体外侧，gxz指向陀螺阴极，gxy与gxx、gxz满足右手定则。动量矩定理及刚体欧拉运动学方程为

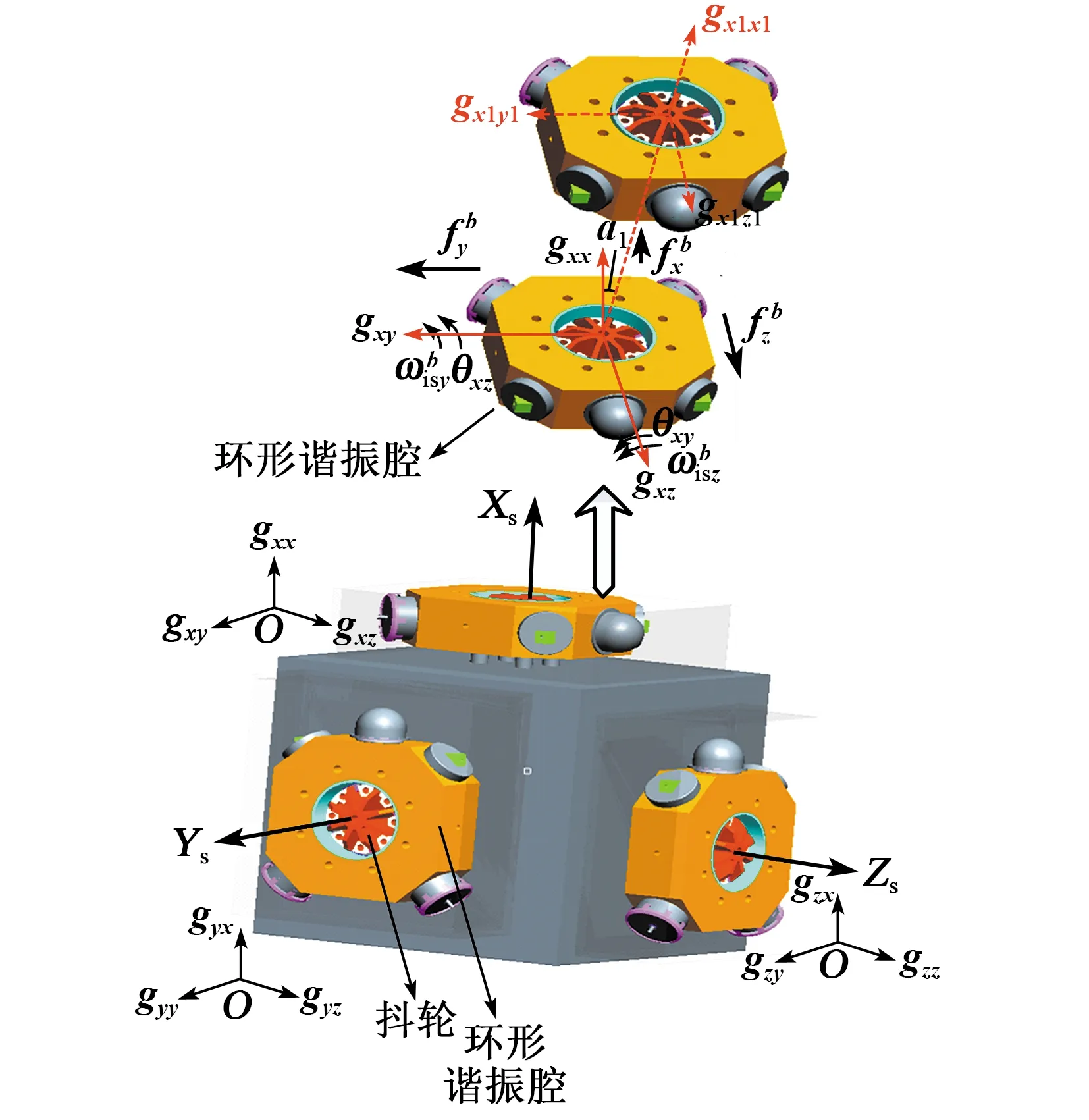
图4 惯性敏感器本体结构示意图

(6)

(7)

(8)

(9)

式中：L为陀螺动量矩；M为陀螺所受力矩；C为抖动轮阻尼系数矩阵；K为抖动轮刚度系数矩阵；Md为抖动驱动力矩；J为陀螺转动惯量矩阵；Θ为陀螺相对安装基座的转动向量；ωis为安装基座相对惯性空间的转动角速度向量。

为分析方便且不失一般性，令X陀螺抖动轴与安装基准面法线平行，环形谐振腔绕陀螺阳极轴gxy转过角-a1(见图4)，与安装基座固连的陀螺坐标系gxx、gxz轴将不再是环形谐振腔惯量主轴，存在惯性积Jxz、Jzx。刚体在与环形谐振腔固连的直角坐标O-gxx1gxy1gxz1下对任意轴v的转动惯量[6]为

Jv=Jx1x1cos2α+Jy1y1cos2β+Jz1z1cos2γ-

2Jy1z1cosβcosγ-2Jz1x1cosγcosα-

2Jx1y1cosαcosβ

(10)

式中：Ji1i1(i=x,y,z)，Ji1j1(i,j=x,y,z;i≠j)分别为刚体相对gxx1、gxy1、gxz1的转动惯量和惯性积；α，β，γ为轴相对坐标系的转角。

当环形谐振腔相对gxy转过角-a1时，则可根据Ji1i1、Ji1j1计算陀螺相对gxx、gxy、gxz的转动惯量：

Jxx=Jx1x1cos2a1+Jz1z1sin2a1

(11)

Jzz=Jx1x1sin2a1+Jz1z1cos2a1

(12)

由于gxy是转动轴，即gxy仍是陀螺的惯量主轴，则：

Jyy=Jy1y1

(13)

Jxy=Jyz=0

(14)

Jxxcos2a1)

(15)

当ωis=0时，式(6)～(9)可简化为

(16)

(17)

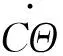
(18)

3 抖动轴失准角影响分析及仿真

为方便对失准角引起的陀螺精度误差进行定量计算，其典型参数如表1所示[7]。表中，θmax为抖动角幅值，ωxz、ωxy为抖动轮横侧向扭转频率。

表1 典型参数列表

由式(11)～(15)可得：

Jxz≈a1·Jz1z1

(19)

由抖动转角θxx=θmaxsin(ωdt) 可得：

(20)

陀螺侧向角刚度为

(21)

将式(19)～(21)代入式(18)，计算可得出θxzmax=1″。令环形谐振腔相对陀螺阴极轴gxz转过35′，同理，θxy max≈1″，有：

θxz=θxz maxsin(ωdt)

(22)

θxy=θxy maxsin(ωdt+φ)

(23)

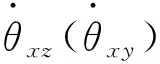
(24)

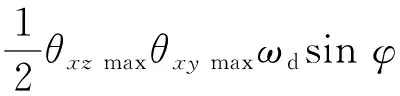
(25)

令a以0.5′为步长从1′连续变化到60′，φ以0.01 rad为步长从0连续变化到1.57 rad(90°)，仿真结果如图5所示。由图可看出，当抖动轴失准角为60′时，由陀螺抖动产生的圆锥误差最大可达0.02 (°)/h。根据式(24)及仿真结果，圆锥误差将随抖动轴失准角的平方量级变化，影响相当可观。当抖动轴失准角小于5′时，由式(24)可得陀螺误差小于0.000 5 (°)/h，不会影响高精度应用场合下的性能。

图5 陀螺误差仿真结果

4 陀螺测试结果分析

选取3只RLG-90型激光陀螺(序号1、2、3)，单陀螺通电3次，计算100 s均值的标准差，结果如表2所示。按照文中抖动轴失准角测试方法对失准角进行测试，结果如表3中序号1，重新对环形谐振腔和抖轮进行粘接，人为增加抖动轴失准角，再次进行失准角测试，结果如表3中序号2，再对各陀螺使用相同设备通电测试，单陀螺通电结果如表4所示。失准角测试现场如图6所示。精度测试现场如图7所示。对比表3、4可看出，抖动轴失准角增加后，各陀螺的3次测试结果的均值变大(精度变差)，且各次测试结果偏差变大，精度偏差约0.003 (°)/h。

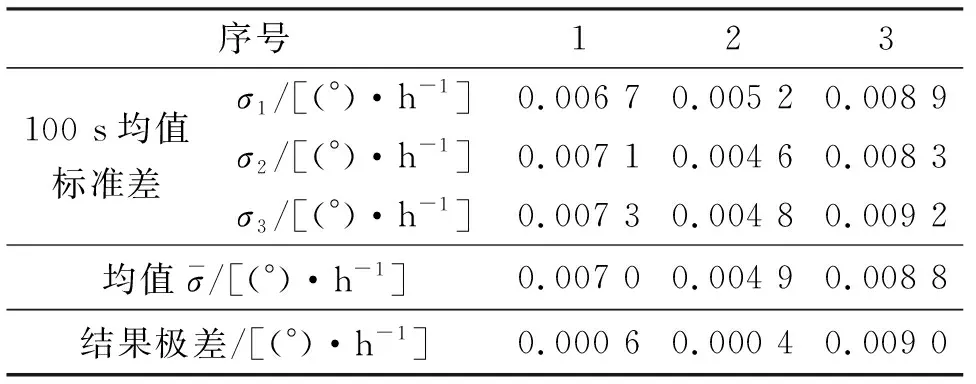
表2 陀螺测试结果(100 s)

表3 陀螺失准角测试结果

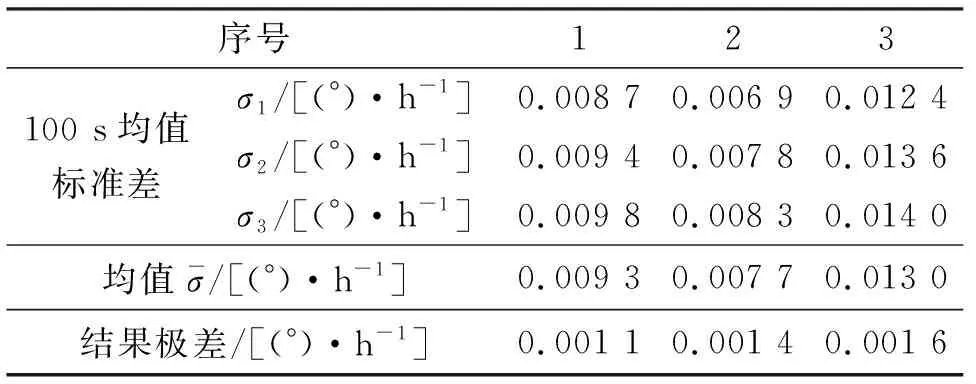
表4 重新装配后陀螺测试结果(100 s)

图6 失准角测试现场

图7 单陀螺测试现场

5 结束语

二频机抖激光陀螺抖动轴失准角通过刚体惯性积使激光陀螺抖动轴、垂直抖动轴阴极指向、垂直抖动轴阳极指向3个轴向发生动力学耦合，环形谐振腔绕抖动轴横侧向的同频角运动将产生绕转动轴的单表级圆锥误差，误差大小与失准角的平方相关。由于单表级的圆锥误差无法通过圆锥误差补偿方法进行补偿，所以在高精度应用场合，需对抖动轴失准角进行严格控制。事实上，激光陀螺环形谐振腔通过抖动轮悬臂安装，在外部力学环境下，抖动轴将发生横侧向弯曲，带动陀螺敏感轴动态偏移，激发陀螺动态误差。近来已有研究关注激光陀螺的重力敏感性[5]和重力场中的零偏变化[8]，即在本文的动力学方程中除抖动驱动力矩外增加了横侧向力矩，在这种条件下，应用此动力学方程将对激光陀螺的动态误差进行进一步分析。