一类面内弯曲模态行波直线超声电机的研究

杨金波，何 勍

(辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001)

0 引言

超声电机利用逆压电效应将电能转化为定子(振子)的振动能，再通过摩擦作用将振子的振动能转化成动子旋转或直线运动的动能[1]。超声电机具有结构简单,功率体积比大,响应快,断电自锁,直接驱动,输出形式灵活及能实现高精度定位等优点，成为多年来一个持续的研究热点，并在机器人、航空航天、医疗生物工程、精密定位和微型机械等高新技术领域有重要应用[2-4]。

直线超声电机已有较成熟的商业应用，如以色列Nanomotion公司生产的直线超声电机已被广泛应用于精密驱动领域。迄今为止，尽管国内许多科技工作者从工作原理、结构设计及摩擦材料等领域进行了很多探索，但国内大多数直线电机存在体积大，输出性能不佳及寿命短等问题[5]。

近年来，国内外许多研究者针对超声电机开展了若干探索工作，许多可满足特殊工作环境的新型结构直线超声电机相继问世，并得到系统的理论与实验研究。张彦虎等[6]设计了一款薄板型直线超声电机，电机薄板振子利用面内纵-弯复合模态驱动动子运动，最大输出力可达3.4 N。Shunsuke Izuhara等[7]提出了一种新颖的面外弯曲-面内纵振复合模态空心矩形振子的直线超声电机，动子在振子的空心矩形结构内做垂直于振子平面的直线运动，该电机输出力为0.5 N。该类复合模态超声电机的频率简并问题，一直是设计与实际调节过程的难点。Liang Wang等[8]提出大推力螺杆式直线电机，定子采用空心金属弹性体，利用两个正交的面内三阶模态产生弯曲行波，驱动螺杆直线输出，该电机有助于简化结构，但施加的预压力仅靠振子圆筒与螺杆间的作用力调节较难，不易控制。Jianye Niu等[9]提出了一种坦克轨道型的行波直线超声电机，振子基于两种扭转模态，利用外表面驱动滑块运动，最大推力可达96.1 N，为设计高性能直线超声电机提供了一条新途径。

本文提出了一种基于面内弯曲模态的含有不完全齿的圆环型行波直线超声电机。它利用圆环外表面的工作齿端面与滑块动子相互接触，以驱动动子运动。针对当前超声电机寿命较短问题，该电机振子可通过轮换不同的工作齿方式来提高超声电机的寿命。

1 电机振子的结构及工作原理

1.1 电机振子的结构

图1为本文所提出电机振子结构。其中用于粘贴4个压电陶瓷片的定位槽与圆环外表面的4组齿均布于圆环内外表面上，每组包含3个齿且与每个陶瓷片定位槽相隔45°，齿高为2.5 mm。压电陶瓷片的极化方向如图1(a)所示，圆环外表面的齿形结构可放大振子周向振幅，整体结构具有一定的对称性，可激发出两个频率相等的正交模态，以保证行波的产生。振子的主体材料为LY12，压电陶瓷片选用PIC181系列，其尺寸为12 mm×6 mm×1 mm。

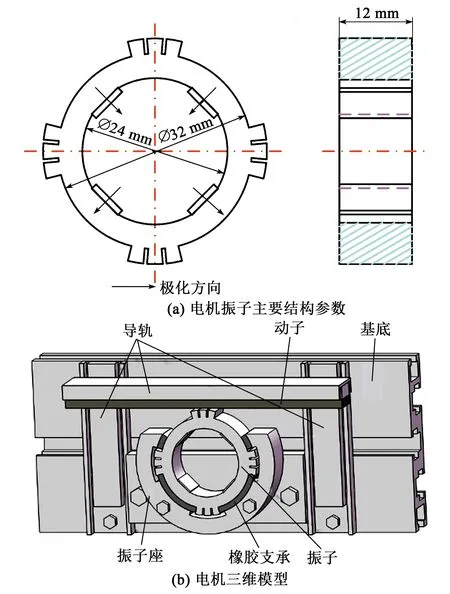
图1 超声电机结构图

接触式超声电机接触部分的磨损将导致电机的输出性能不佳，从而造成超声电机工作寿命较短。国内外学者在摩擦材料领域有诸多探索，在一定程度上提高了超声电机的寿命。本文电机振子采用4组均布于圆环外表面的工作齿结构，工作时，仅有一组参与驱动，当工作齿因磨损不能满足工作需求时，可将振子沿圆周方向旋转90°来轮换另一组新的工作齿，从而提高超声电机的使用寿命。

1.2 工作原理

本文提出基于面内三阶弯曲振动模态为工作模态的振子，分别给对面粘贴的两组压电陶瓷片施加同频同幅的正、余弦电信号。A相和B相激励产生的两个驻波可表示为

wA(x,t)=W0·sin(kx)·sin(ωt)

(1)

wB(x,t)=W0·cos(kx)·cos(ωt)

(2)

式中：w(x,t)为振子齿所在外圆弧面的弯曲挠度，其振幅为W0；x为沿圆周方向的的角度坐标；k为振子驻波弯曲振动的阶次。

以圆环型振子外表面齿形结构端面的一点为参考点，两相驻波在该点处叠加得到弯曲行波：

w(x,t)=wA(x,t)+wB(x,t)=

W0cos(kx-ωt)

(3)

三阶面内弯曲模态的波长对应的圆周为120°， A、B两相激励的两组陶瓷片间隔为90°，即3λ/4(λ为波长)，两组陶瓷片可产生时间和空间上相位差均为的π/2的驻波，理论上可以合成行波。

2个单相驱动产生的驻波在时间和空间相位上均相差90°，每组陶瓷片激发出的驻波在圆环型振子表面叠加产生沿周向运动的行波，被激发的两个同频正交面内三阶弯曲模态相互叠加,在圆环型振子外表面的齿形结构端面形成椭圆运动[1]，施加一定的预压力，使振子和动子相互接触，则在摩擦力作用下振子驱动滑块动子运动。

2 电机振子的有限元仿真

本文用有限元软件ANSYS进行设计与仿真，在自由边界条件下计算得到2个基本振动模态B03的振型，如图2所示。

图2 两相电机振子的B03模态分析

通过有限元模态分析，选用振动频率处于超声频段但又不很高的三阶面内弯曲模态，2个正交模态对应的频率为fA=fB=31 561 Hz。由于振子的结构具有一定的对称性，易激发2个同频的正交模态。由图2可看出，陶瓷片的粘贴位置位于工作模态弯曲应变最大的区域。

设计中，仅对振子进行振型分析不够。即使设计的振子具有工作所需振型，但如果驱动信号不是最优，也不能使振子产生足够大振幅。具体施加多大的驱动信号，能得到多大的振幅，需要对振子进行谐响应分析。分别对2组陶瓷片施加峰值为40 V的正弦信号，频率分析区间为29.6～ 33.6 kHz。振子在共振频率的电压激励下，驱动足上的质点r、z方向上均有一定的振幅。为了方便实验结果与测试结果对比，质点选取在振子外表面齿形结构端面的中点处一点，其分析结果如图3所示。

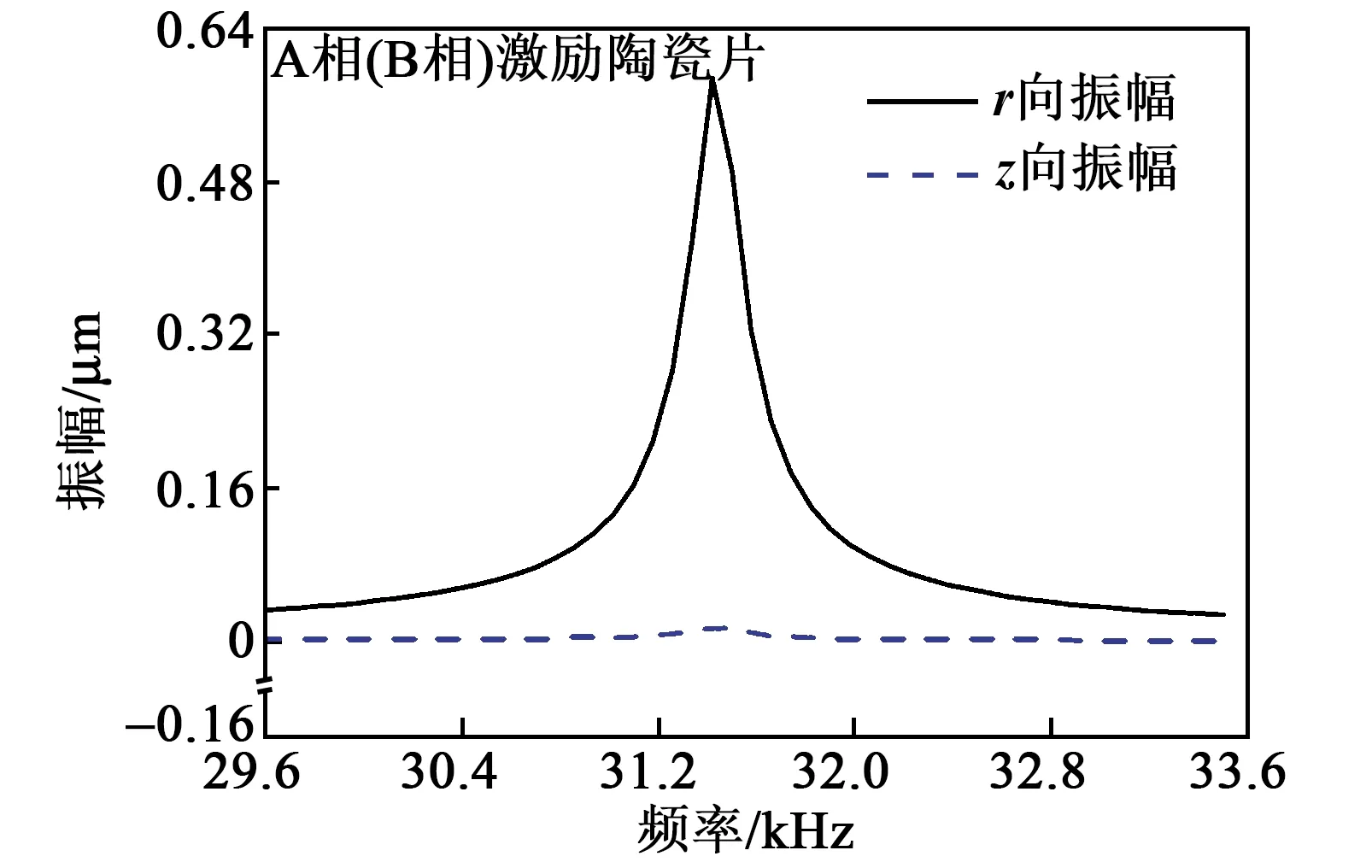
图3 电机振子的谐响应分析

在2组陶瓷片上分别施加峰-峰值为40 V的正余弦信号，对振子进行瞬态分析，时间为100个周期，选择齿外端面的中点提取其运动情况。图4为电机振子的瞬态分析。由图可知，经过一定周期后，提取的点在r-q平面内的运动轨迹为椭圆，说明此方案可行。

图4 电机振子的瞬态分析

3 超声电机的实验研究

3.1 超声电机的制作

根据图1的结构形式及参数研制了原理样机及实验装置。将沿厚度方向极化的压电陶瓷片通过环氧树脂粘贴在圆环型振子内侧的4个定位槽上。为便于固定振子，设计并加工了一个专用的振子基座，为了减少基座对振子振动的影响，振子与基座间采用橡胶材料隔离。动子为尺寸100 mm×10 mm×3 mm的滑块，材料为H59。动子采用3个移动导轨确保其直线运动时，通过可调预压力贴紧在振子的驱动齿上。样机的安装如图5所示。

图5 直线超声电机的原理样机

3.2 电机振子的特性测试

使用德国polytec公司生产的OFV-5000型激光测振系统测试圆环型振子的振动特性。选取圆环型外表面齿形结构端面的中点进行扫频实验。图6为振子在谐振点附近的幅频特性曲线。

图6 电机振子的幅频特性测试结果

实验结果表明，在施加电压峰-峰值为40 V时，实测振子的两个正交面内弯曲模态谐振频率为30.459 kHz，有限元分析结果为31.561 kHz，误差为3.4%。振子在29.5～31.5 kHz内无其他干扰模态。

在激励频率为30.459 kHz时振子的振幅分布情况如图7所示。在振子外表面的齿形结构端面中点处沿圆周方向旋转1周，得到实际的测振结果。由图可看出，在该频率下振子的面内三阶弯曲振型被激发出来，与ANSYS的分析结果基本相同，加工的振子能合成预期的行波运动。

图7 电机振子的激光测试曲线

3.3 电机的输出特性测试

利用信号发生器和功率放大器驱动电机，在激励信号峰-峰值为240 V，激振频率为30.459 kHz，预压力为0.6 N时，对电机的输出特性进行测试。实验中输出力是通过动子提升不同质量的砝码来衡量。图8为不同激励电压下电机的空载速度。图9为不同激励电压下电机的最大输出力。由图8、9可知，激振频率为30.459 kHz时，空载速度与最大输出力均随着电压的增大而变大。激励电压为80～280 V时，空载速度从4.15 mm/s增加到110.26 mm/s，最大输出力从4 mN增加到117 mN。由此可知，通过改变激励电压即可控制电机的速度和最大输出力。

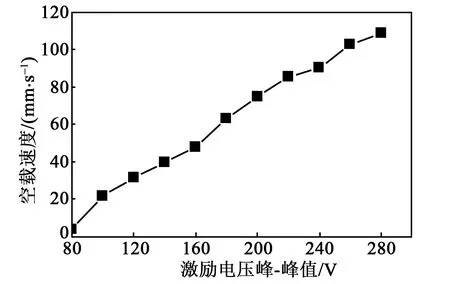
图8 不同激励电压下电机的空载速度

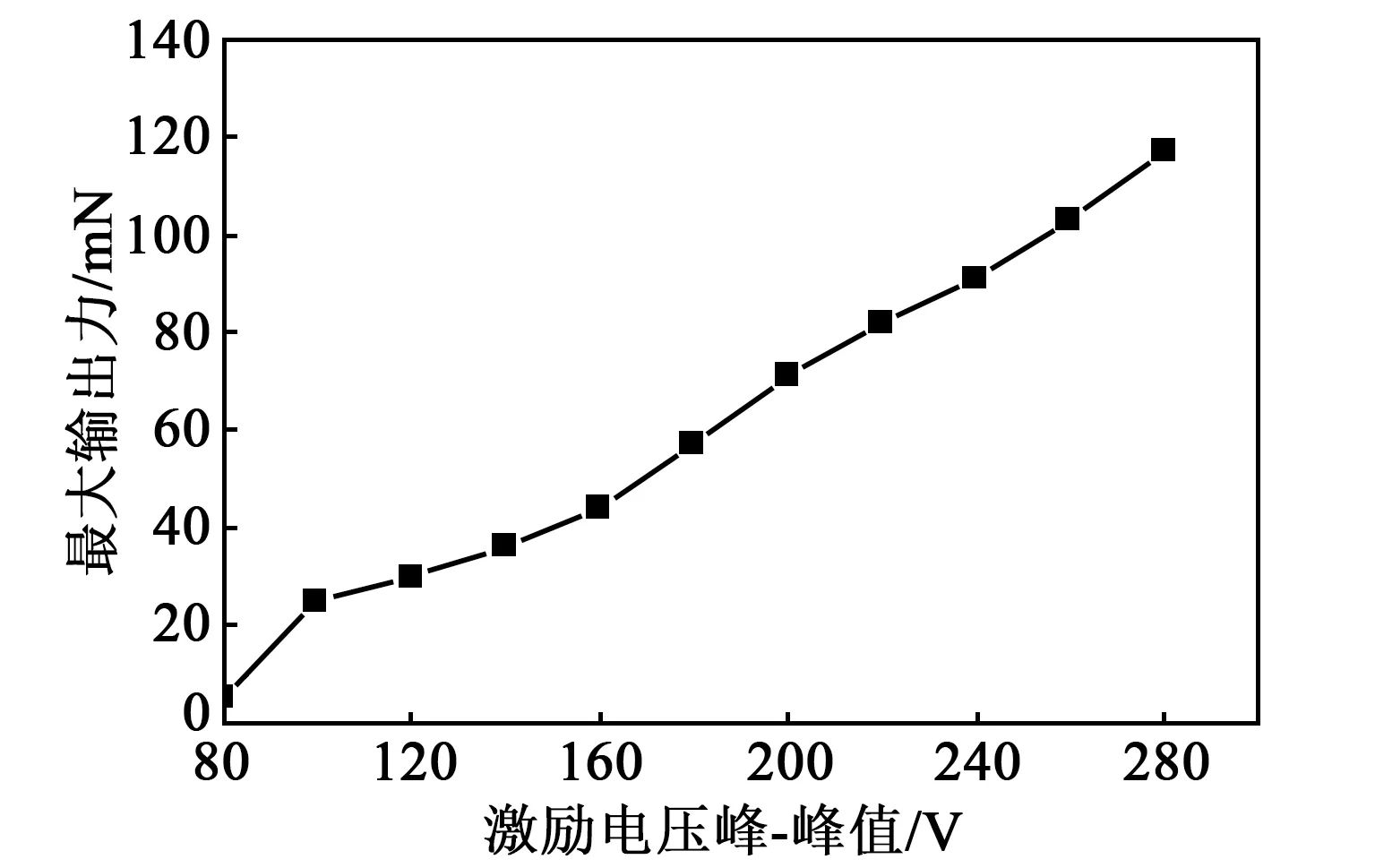
图9 不同激励电压下电机的最大输出力

在峰-峰值240 V激励电压下，通过悬挂不同质量砝码来改变负载，测得在不同输出力下动子的速度如图10所示。由图可知，动子速度随着输出力的增加而减小，电机的空载速度为102 mm/s，最大输出力为90 mN。

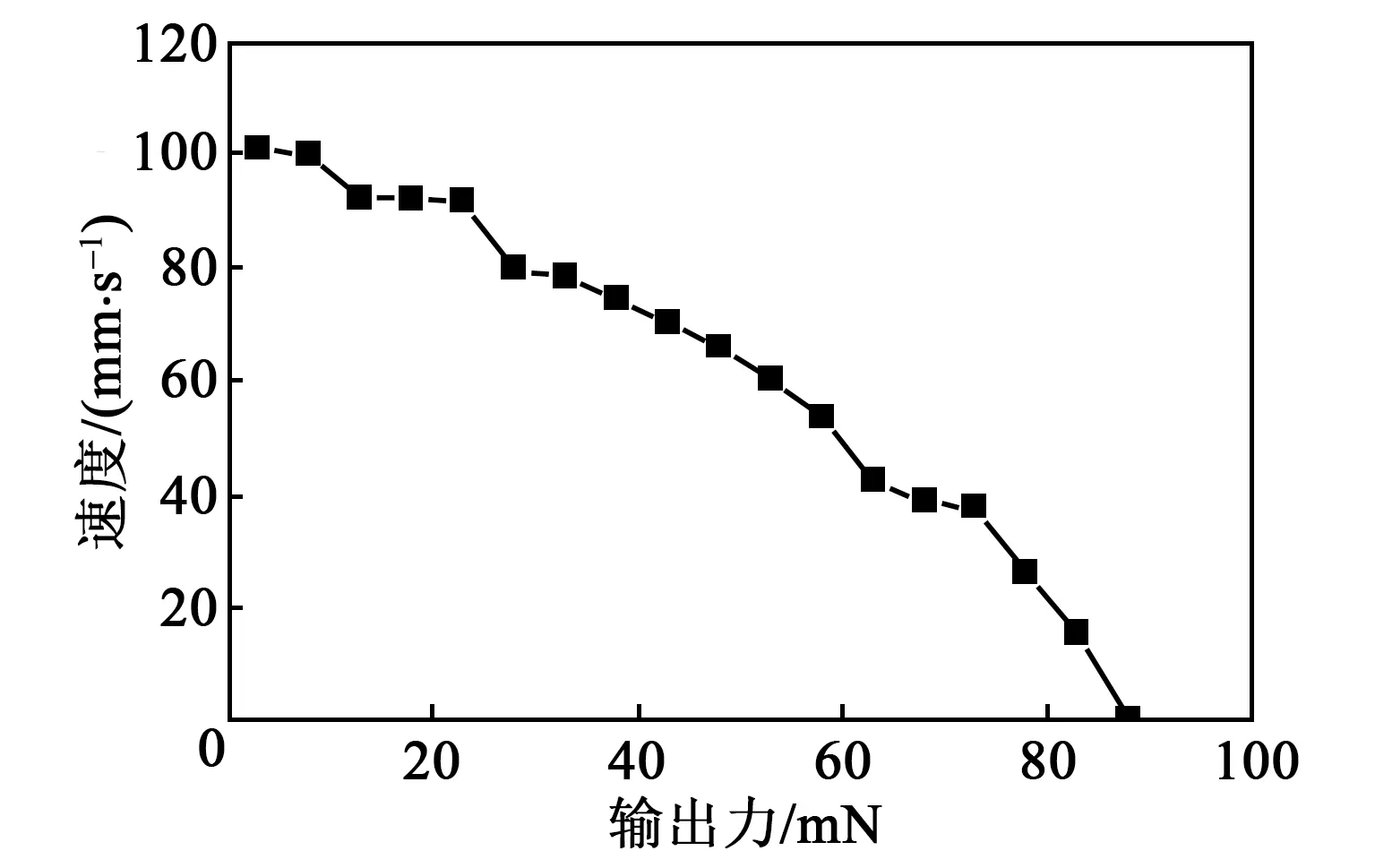
图10 在不同输出力下电机的速度

4 结束语

本文提出了一种基于面内弯曲模态的行波直线超声电机。该电机振子的结构为4组齿均布于圆环外表面，通过轮换不同工作齿的方式提高电机寿命。电机利用圆环的两个三阶正交面内弯曲模态工作，驱动动子做直线运动。借助于有限元软件对本振子进行了设计与仿真，确定了尺寸参数、工作模态和频率。研制了原理样机并进行了相关的性能测试，实验结果表明,该电机在激励电压峰-峰值为240 V，激振频率为30.459 kHz时，电机运行平稳，最大输出力为90 mN，电机的空载速度为102 mm/s。