基于率相关迟滞模型的压电微动平台前馈控制
2023-01-30王博文崔玉国谢启芳
王博文,崔玉国,谢启芳,陈 攀
(宁波大学 机械工程与力学学院,浙江 宁波 315211)
0 引言
压电微动平台是一种结构紧凑、运动行程为亚毫米级、位移分辨率达到纳米级的微定位机构,其被广泛用于微机电系统、航空航天、超精密加工和光学精密工程等高精密定位领域[1-2]。根据逆压电效应,压电微动平台中的压电执行器会在外加电压的驱动下发生微位移形变,通过柔性铰链传递微位移,从而实现微动平台的纳米级定位和运动[3]。但压电执行器自身存在迟滞、蠕变及振荡等非线性特性,其中迟滞特性会对压电微动平台的定位精度带来较大影响,造成压电微动平台的输入电压与输出位移之间呈非线性关系[4]。
为了提高压电微动平台的定位精度,需要采用相应的控制方法来消除其迟滞误差。目前常用的控制方法有前馈控制[5]、反馈控制[6]和复合控制[7]。前馈控制是一种基于迟滞逆模型的开环控制,无需传感器,成本低,易实现,但控制精度依赖于所建立的迟滞模型的精度。反馈控制是一种闭环控制,控制精度相对较高,但因其信号通过传感器实时反馈,系统成本高,且在某些精密定位领域中受空间限制,有时无法安装传感器。复合控制是前馈控制和反馈控制的结合,控制精度高,响应速度快,但同样受空间限制,有时无法安装传感器,且系统成本也较高。
为降低压电微动平台控制系统的成本,并在空间受限时保证系统仍具有较高的定位精度,常采用前馈控制方法来提高压电微动平台的定位精度。前馈控制的关键在于建立能精确描述压电微动平台输出位移和输入电压关系的迟滞模型,对提高前馈控制的精度具有重要意义。目前常用的迟滞模型主要有 Bouc-Wen模型、Preisach模型、PI模型和KP模型等,其中PI 模型因其结构简单、求逆运算方便等优点而被广泛应用于迟滞建模上[8]。研究发现,在驱动信号频率的变化下,压电执行器的迟滞特性将发生动态变化,即率相关性。为了提高PI迟滞模型的精度,Aljanaideh等[9]通过构造率相关的Play算子和动态密度函数,建立了广义速率相关的PI模型,有效地抑制了迟滞误差。Zhou等[10]将驱动信号的动态变化率引入经典Prandtl-Ishilinskii(PI)模型的静态权值中,构成率相关的迟滞模型,取得了不错的补偿效果。目前率相关PI迟滞模型多为整体式建模,通过引入同速率相关的函数来建模,这种建模方法不仅增加了所建迟滞模型的复杂度,模型求逆难,且需要进行大量实验,建模所需时间较长。
本文采用分离式率相关迟滞建模方法,通过将压电微动平台的迟滞特性拆分为静态迟滞特性与线性动力学特性,建立了分离式率相关Modified Prandtl-Ishilinskii(MPI)迟滞模型,进而设计出前馈控制器对平台进行控制,以消除平台的动态迟滞误差。
1 平台系统动力学建模
1.1 平台结构
本文的研究对象为x-y-θz三自由度并联压电微动平台,如图1所示。平台整体结构包括台体、外框体和内框体,台体中的导向与解耦机构呈空间交叉分布。该平台具有良好的导向及解耦功能、动平台大和结构紧凑等优点。
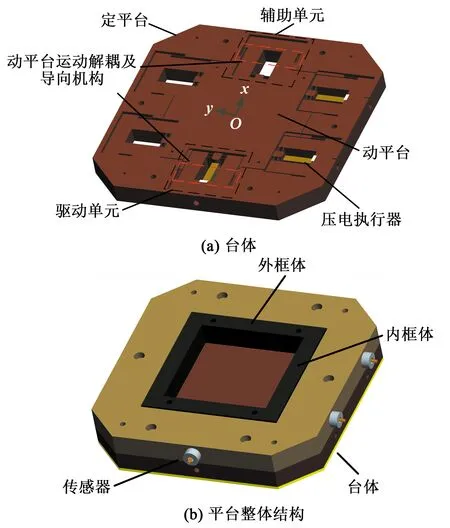
图1 平台结构模型
1.2 平台动力学模型
从动力学角度出发,压电微动平台可假设为质量-弹簧-阻尼系统。考虑到系统中的接触刚度以及机构的解耦性能,所设计的柔性机构动力学模型如图2所示。
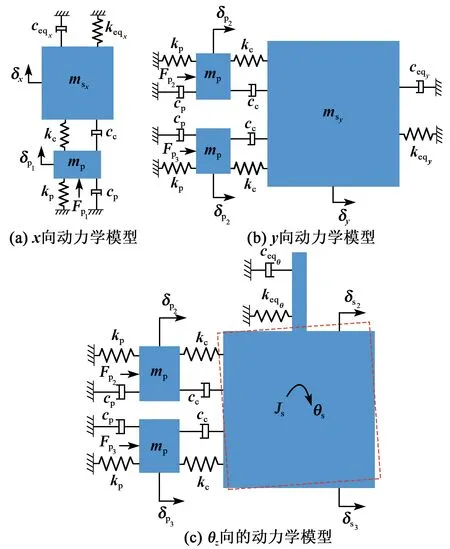
图2 平台动力学模型
图2中mp、kp、cp分别为压电执行器的等效质量、等效刚度和等效阻尼,Fpi(i=1,2,3)为压电执行器的驱动力,δp1、δp2和δp3分别为压电执行器在x、y和θz向上的输出位移,kc、cc分别为压电执行器与微动平台的接触刚度和等效阻尼,ms、Js分别为微动平台的等效质量和转动惯量,ceqx、ceqy和ceqθz分别为微动平台柔性机构在x、y和θz向上的等效阻尼,δx、δy和δθz分别为微动平台在x、y和θz向上的输出位移。
根据图2中的平台动力学模型及牛顿第二运动定律,微动平台x向、y向和θz向的动力学方程如下:
(1)
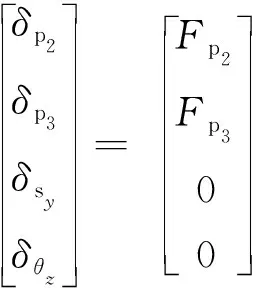
(2)
2 平台前馈控制
2.1 平台率相关迟滞模型的建立
由于压电微动平台在不同频率驱动下表现出的率相关迟滞特性(即动态迟滞特性)可分解为静态迟滞特性与线性动力学特性,因此,平台的率相关迟滞模型(即动态迟滞模型)可通过平台静态迟滞特性的模型(即静态迟滞模型)与平台动力学特性的模型(即线性动力学模型)的串联进行描述。
由于PI模型具有算法简单,运算量小,便于求逆等优点,因而被广泛用来描述具有迟滞特性的系统。PI迟滞模型主要用来描述具有奇对称迟滞特性的系统,而压电执行器的迟滞特性表现为非奇对称性。因此,本文在构成常规PI迟滞模型的Play算子(见图3)中引入具有非奇对称性的Stop算子(见图4),对其进行改进,进而得到PI迟滞模型与Stop算子串联叠加的改进PI迟滞模型(即MPI)。
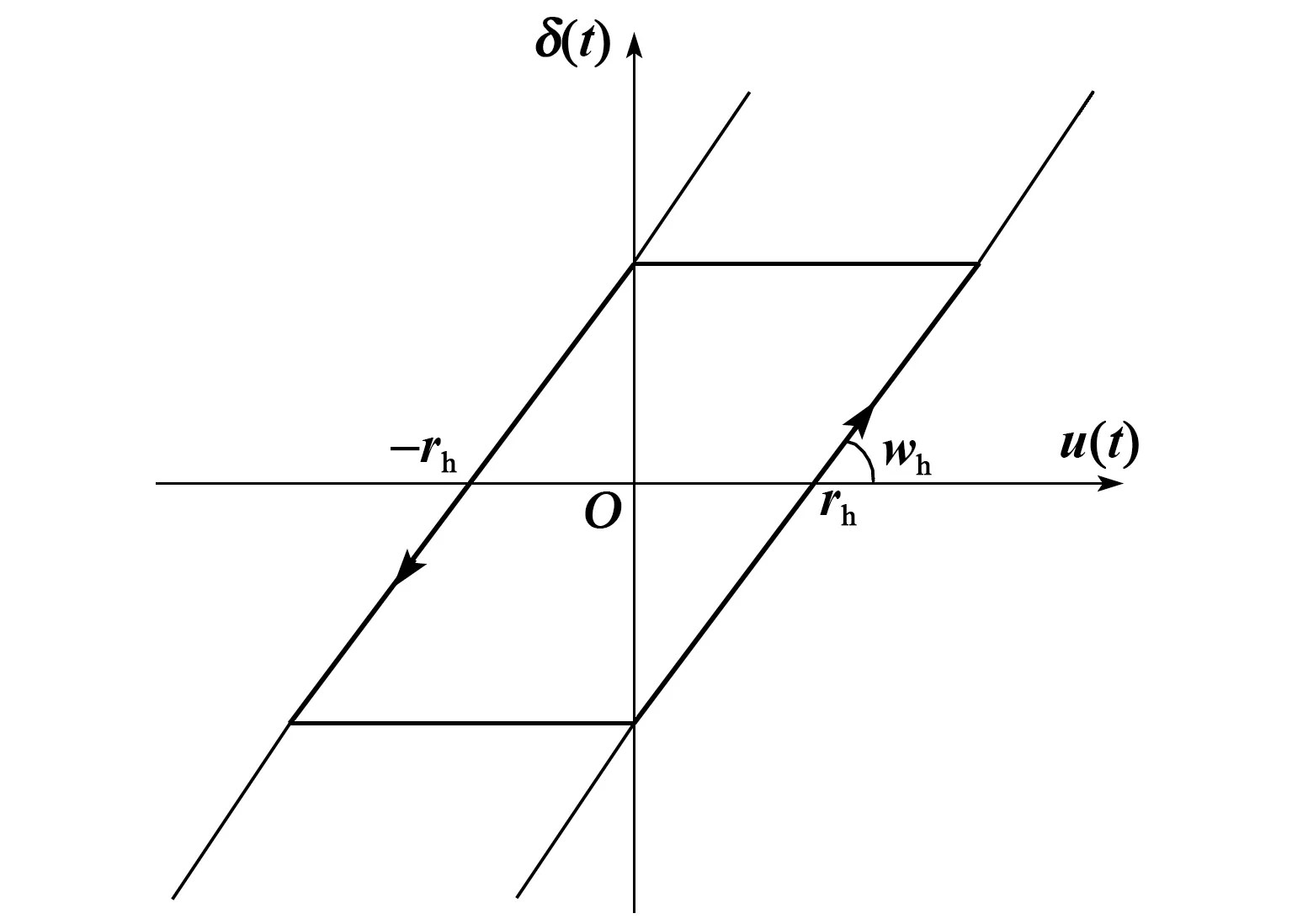
图3 Play算子
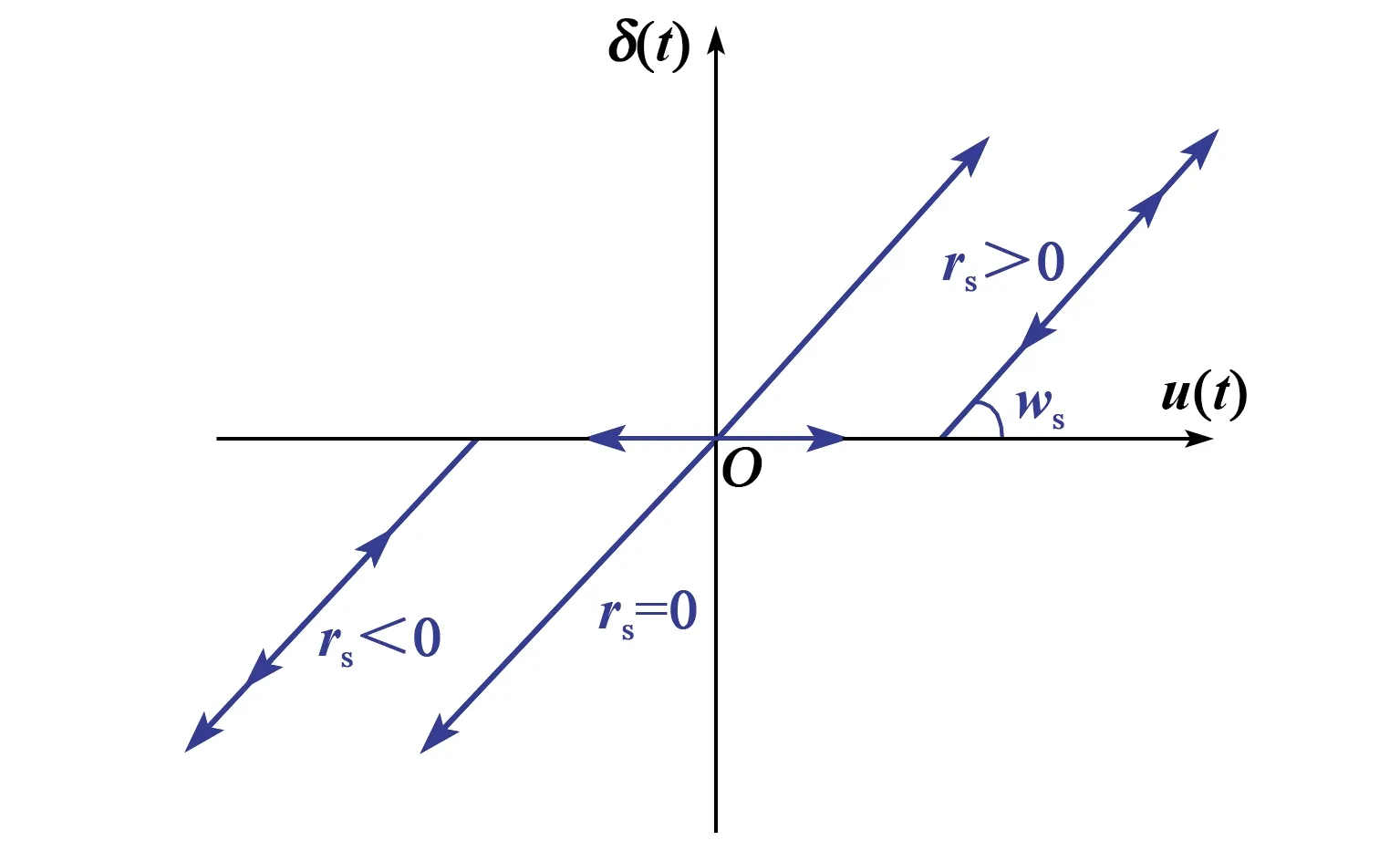
图4 Stop算子
压电微动平台的线性动力学特性可采用欠阻尼二阶系统来描述。本文在辨识平台的线性动力学模型时,采用数值计算软件Matlab中的辨识模块,并基于自回归滑动平均模型(ARX)来辨识。
本文所提出的平台率相关迟滞建模策略如图5所示。图中,u(t)是压电微动平台的输入电压,δ(t)是u(t)经过MPI模型后的中间变量,y(t)是在输入电压u(t)下平台的实际输出位移,N(·)和G(z)分别是MPI模型和ARX模型的数学表达。该模型简单,无需大量实验,建模周期短,克服了现有的整体式率相关迟滞建模方法的模型复杂、不易求解、建模周期长等不足。

图5 平台的率相关迟滞建模策略
本文的MPI静态迟滞模型、ARMAX线性动力学模型、率相关MPI迟滞模型的表达式:
(3)
2.2 平台前馈控制器的设计
本文压电微动平台的前馈控制器设计思路:根据前面所建立的率相关MPI迟滞模型求取其逆模型,并将迟滞逆模型作为前馈控制器串联到压电微动平台前,用于补偿压电微动平台的动态迟滞误差。前馈控制方案框图如图6所示。将期望输出位移yd(t)输入到前馈补偿控制器,得到前馈补偿控制电压u(t),然后将u(t)输入压电微动平台中得到前馈控制后的实际输出位移y(t)。

图6 前馈控制方案框图
本文提出的率相关MPI模型是一种分离式结构的迟滞模型,因此,其逆模型也具有分离式结构,由动态线性逆模型与静态迟滞逆模型串联构成,如图7所示。其中ARX逆模型、MPI逆模型的表达式为

图7 率相关MPI迟滞逆模型结构框图

(4)
(5)
联立式(4)、(5),得到前馈控制器的控制律为
(6)
3 实验验证
3.1 平台位移测试系统
图8为压电微动平台位移测试实验系统。系统由计算机、数据采集卡、驱动电源、压电执行器、微动平台和电容式位移传感器构成。

图8 平台位移测试实验系统
3.2 控制实验结果
3.2.1 阶跃响应
图9为平台3个方向在无前馈控制和有前馈控制下的阶跃响应结果。由图可知,在无前馈控制器作用下,x、y和θz向的响应时间分别为6.36 ms、7.64 ms和9.20 ms,稳态误差分别为0.45 μm、0.79 μm和6.33 μrad;有前馈控制器作用下,x向、y向和θz向的响应时间分别为6.64 ms、7.92 ms和8.56 ms,稳态误差分别为0.19 μm、0.41 μm和1.21 μrad。由此可见,所设计的前馈控制器有效地提高了平台的定位精度。

图9 阶跃响应
3.2.2 正弦轨迹跟踪
图10为平台3个方向在前馈控制器作用下跟踪1 Hz和20 Hz的正弦轨迹跟踪结果。在跟踪1 Hz参考位移时,x、y和θz向的最大误差分别为0.26 μm、0.26 μm和2.11 μrad;跟踪20 Hz参考位移时,x向、y向和θz向的最大误差分别为0.32 μm、0.37 μm和2.60 μrad。由此可见,前馈控制下平台的动态迟滞误差得到有效补偿,并随着跟踪信号频率的增加,平台3个方向上的最大控制误差均无显著增大,表明所设计的前馈控制器具有良好的率相关特性。
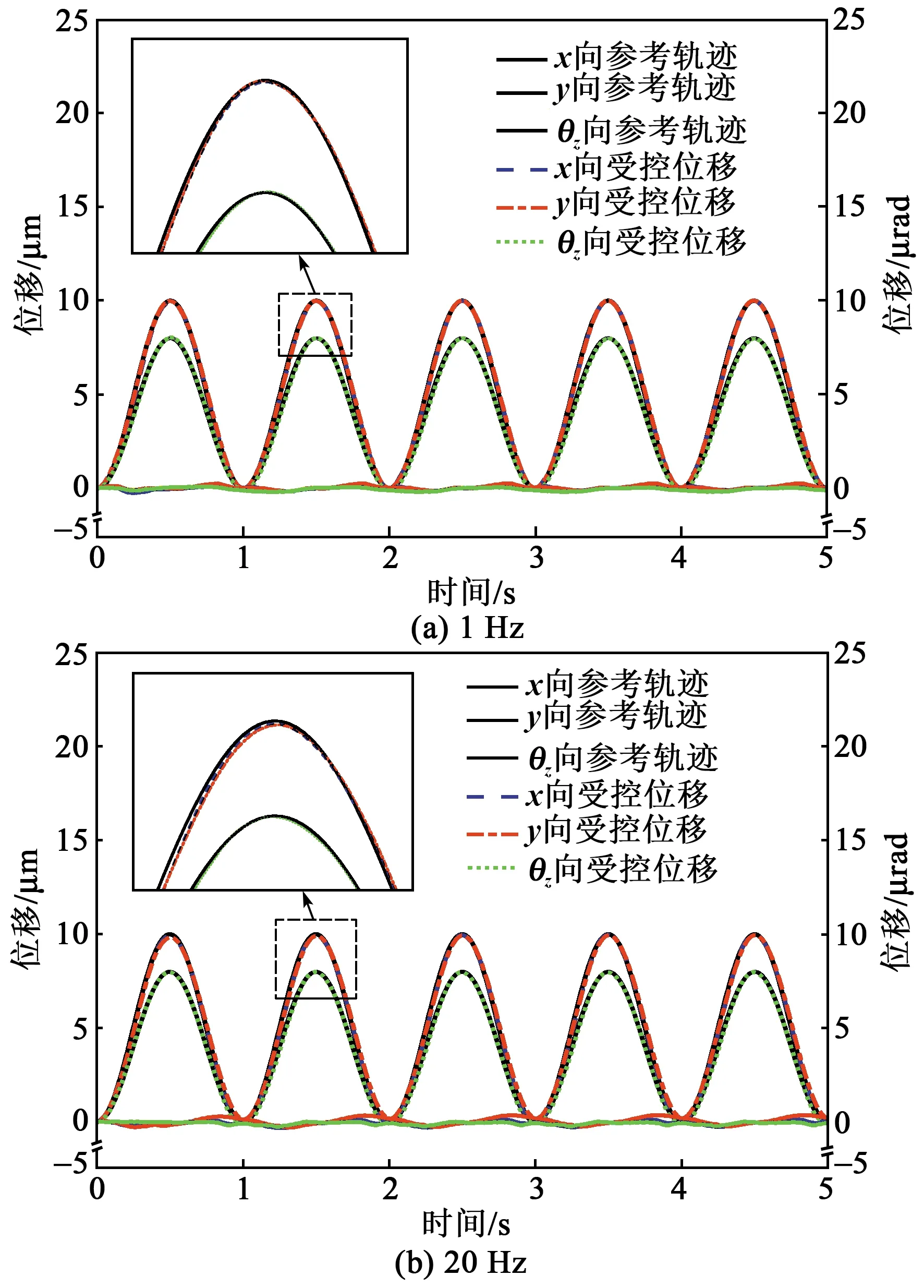
图10 正弦跟踪结果
4 结束语
本文采用分离式率相关迟滞建模策略,在传统PI迟滞模型的基础上加以改进,得到率相关MPI迟滞模型。基于率相关MPI迟滞逆模型,采用直接逆补偿控制方案,设计了平台的前馈控制器。控制实验结果表明,所设计的前馈控制器能在一定程度上消除平台的动态迟滞特性,提高平台的定位精度。
