Impingement and mixing dynamics of micro-droplets on a solid surface

Guina Yi, Ziqi Cai,*, Zhengming Gao,*, J.J.Derksen

1 Beijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China

2 State Key Laboratory of Chemical Resource Engineering, School of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, China

3 School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK

Keywords:Droplets impingement Mixing behavior Mixing time Concentration distribution Many-body dissipative particle dynamics

ABSTRACT The hydrodynamics and mixing during the nonaxisymmetry impingement of a micro-droplet and a sessile droplet of the same fluid are investigated by many-body dissipative particle dynamics (MDPD) simulation.In this work, the range of the impingement angle (θi) between the impinging droplet and the sessile droplet is 0°–60°and the contact angle is set as 45°or 124°.The droplets impingement and mixing behavior is analyzed based on the droplet internal flow field,the concentration distribution and the time scale of the decay of the kinetic energy of the impinging droplet.The dimensionless total mixing time(τm) is calculated by a modified mixing function.With the Weber number (We) ranging from 5.65 to 22.7 and the Ohnesorge number (Oh) ranging from 0.136 to 0.214, we find τm hardly changes with We and Oh.Whereas, θi and surface wettability are found to have a significant effect on τm.We find that θi has no clear effect on τm on a hydrophobic surface, while on the hydrophilic surface, τm increase with the θi.Thus, reducing the impinging angle is a valid method to shorten the τm.

1.Introduction

Droplets impinging on solid surfaces is common in industrial and technological processes, such as electro-spraying [1], inkjet printing [2,3], drug delivery [4], and self-cleaning [5].Generally,there are three types of impingement and mixing of two droplets on a solid surface, dependent on their relative position when approaching the surface, see Fig.1.(a) The two droplets impinge on the surface simultaneously;(b)the successive droplets impinge on the surface; (c) the first droplet is in a sessile and equilibrated state on the surface and is hit by the second incoming drop.Here,we review the literature associated with the last, ‘‘long spacing”scenario (Fig.1(c)).

Fig.1. Schematic representation of spatial distributions of two droplets impact on a surface.

When the spacing is large enough, the leading droplet can be regarded as stationary (sessile) when the impinging droplet collides with it.In this case, the impinging droplet could rebound or coalesce after collision.During the coalescence process, there are generally three stages, namely film drainage [6], film rupture and bridge growth [7].The coalescence process of two droplets has been investigated in many previous works [8,9], especially for cases in which droplets are moving slowly relative to one another

When we talk about impingement or collision, the relative motion between droplets cannot be ignored.In the case of a head-on collision (the left side scenario of Fig.1(c)), Fujimotoetal.[10] observed a circular liquid crown after droplets collision,which was on account of a large pressure gradient near the free surface.Wakefieldetal.[11] pointed that the energy dissipation contributed to the crown formation.They also found that half of the kinetic energy of the impacting droplet was dissipated when approaching to the maximum spreading diameter.Besides droplet velocity, the relative size of two droplets [12,13] and surface wettability [14] has also been found to affect the droplets impingement dynamics.

As for offset collision(Fig.1(c)–the middle scenario),the effect of the lateral offset extent between the impinging and sessile droplets on producing a stable line has been experimentally investigated by Soltmanetal.[15] and Stringeretal.[16].Duineveldetal.[17] and Kuetal.[18] studied the influence of surface property on line printing.Based on their work, the receding contact angle was a key parameter to affect the retracting behaviors of the contact line.Leeetal.[19] experimentally found that droplets with low viscosity resulted in disconnection which was undesired in line printing.An empirical correlation was proposed by Lietal.[20] to predict the spread lengths of ethylene glycol droplets.Sarojinietal.[2]studied impingement of PEDOT:PSS droplets.This is a non-Newtonian liquid used for inkjet printing.They proposed a semi-analytical expression to predict the droplet spreading for offset collision in ink jetting.

During the impingement, the time scales and levels of liquid mixing in the merged droplet on the surface have been studied experimentally and computationally by a number of researchers.Castrejón-Pitaetal.[13] studied the mixing behavior between glycerol and water droplets by coloration method.They pointed that the presence of solid surface hindered the mixing.However,the mixing could be improved by stretching and folding the droplets, which could be easily achieved by setting baffles [21] or applying long serpentine channels[22,23]in microchannel device.For’open-surface’ droplet-based microfluidics, a wettability gradient surface[24–26]is a common way to promote the droplet mixing.Recently, Sykesetal.[27] found that the mixing could be improved by the formation of an internal jet.The influence of substrate wettability, the volume ratio and droplet viscosity on the formation of the jet were studied by means of experiments and numerical simulations.Besides passive method, active method applying external force such as magnetic[28],electric[29],acoustic[30]and thermocapillary[31]force can also be used to enhance the mixing efficiency.

For a better understanding of the mixing performance of coalescing droplets on a surface, micro-PIV [32] and micro-LIF [33]techniques are widely applied for droplets of millimeter size.Micro-PIV is an efficient method to track the internal flow of the merged droplet and micro-LIF can be used to visualize the mixing patterns.Based on micro-LIF,the evolution of a mixing process can be quantified by calculating the mixing indexMi, whereMiis related to the concentration of fluorescent tracer [26].

For small length scales, simulation is an efficient way to study the free droplet mixing behavior.Through molecular dynamics(MD) simulations, Paketal.[34] studied the mixing of water nanodroplets in three dimensions.In their study,themixingfunctionm(τ) along one Cartesian coordinate directionxwas calculated as follows:

From the literature reviewed above, we see that the mixing dynamics between the droplets plays an important role in the droplets pattern and the control of product quality.Most of the numerical works performed so far focus on the vertical impingement.Studies of an impinging droplet colliding with a sessile droplet under an angle are limited.In the practical application, the droplet generally has a tangential or lateral speed, especially in the spraying process.Recently,a convenient method to administer sprayable drugs for post-surgical cancer treatment was reported[35].In this method,the fibrinogen solution and thrombin solution were sprayed in the form of micro droplets onto the tumour surface respectively.This mixture formed a gel which helped in inhibiting the local tumour recurrence and the development of distant tumours.However, after being sprayed, it cannot employ external forces to enhance the mixing between droplets.Therefore,it’s necessary to realize how the mixing time of a free droplet impingement on a sessile droplet under various impinging angles was affected, which is the focus of the present work.

In this study,the three-dimensional many-body dissipative particle dynamics (MDPD) simulation was conducted to investigate the effect of impinging angle on droplets impingement and mixing behavior on surfaces with different wettability.Inertial effects and droplet properties such as droplet velocity,surface tension and viscosity were considered.These effects were quantified in terms of Weber number (We) and Ohnesorge number (Oh).All the simulations in this work were programmed in a modified MDPD code based on the LAMMPS [36] framework.

The rest of this paper is organized as follows: the numerical method and parameters applied in this study are given in Section 2.The results and discussion are described in Section 3, where we firstly study the droplets impingement behavior through snapshots, time series of contact points and the velocity field plots.Then the mixing performance is analyzed by mixing time, including the duration of convective stage,the duration of diffusive stage and the total mixing time (τm).Thirdly, the influence of impingement angle, surface wettability,WeandOhon the τmis studied.Finally, conclusions are provided in Section 4.

2.Numerical Method

2.1.MDPD method

The MDPD method is a modification of the original dissipative particle dynamics (DPD) method with the purpose of simulating the coexistence of vapor and liquid[37–39].Examples include fluid flow in nanoporous shales[40],droplets on solid surfaces[41]and gas bubble dynamics [42].In MDPD, particles interactviaforces.The interaction force Fijbetween particleiand particlejhas three contributions: Fij=[38].

where γ is the friction coefficient, δ is the noise amplitude; ξijis a random Gaussian number with zero mean and unit variance.vij=vi– vj,rij= |rij| =ri– rjstand for the relative velocity and distance between two particlesiandj, respectively; eij=rij/|rij| denotes the unit vector from particlejto particlei.A common choice for the weight functionwR(rij) iswR(rij)=1 -rij/rc.The fluctuationdissipation theorem is satisfied when δ2=2γkBTandwD(rij)=[wR(-rij)]2,wherekBis the Boltzmann’s constant andTis the system temperature [43].Δtis the time step.

whereAijwC(rij) represents the long-range attractive part andrepresents the short-range repulsive part.Generally,Aij> 0 andBij< 0.The weight functionwC(rij)=1 -rij/rcandwd(rij)=1 -rij/rdwith the cutoff rangercandrd.

The local density ρ at the location of particleican be obtained by, wherewρ(rij)=[38,44].

2.2.Simulation setup

The schematic representation of our simulation system is depicted in Fig.2 with two droplets of the same liquid.In the present study,the interaction parameters between liquid particles are the same as in our pervious report[45],which was on the interaction of droplet with patterned surfaces,i.e.,Aij=-40,Bij=25,rc=1.0, andrd=0.75.For this set of parameters, the density and the surface tension of the liquid are determined to be ρ=6.09 and σ=7.51 based on individual simulations following the methods according to [45,46].The scaling coefficients between the physical and MDPD units areLMDPD=1.32 × 10-6m,MMDPD=4.0 1 × 10-16kg, andtMDPD=2.31 × 10-7s according to our previous report [45].The substrate is made of frozen particles randomly placed and the substrate is of the same density as the liquid.The bounce-forward[47]boundary condition is applied.The impinging droplet of radiusRc=14 consists of 69849 MDPD particles and the sessile droplet has the same volume, density ρ, surface tension σ and dynamic viscosity μ as the impinging droplet.

In this simulation,the Bond numberBo=(gthe gravitational acceleration)is much smaller than 10-3so that the effect of gravity is neglected.A standard velocity–Verlet algorithm is used for the simulation and the time step is set to Δt=0.01 in MDPD unit [45].

The simulations are performed in a three-dimensional (3D)computational domain of size 150 × 100 × 70, with periodic boundary condition in thexandydirection with the coordinate system defined in Fig.2.First, the sessile droplet is obtained by releasing a spherical droplet to the substrate without velocity.By tuning the long-range attractive part coefficient between the liquid particles and the solid particlesAsl,we can obtain the desired substrate wettability.After the droplet reaches an equilibrium state with a static contact angle θc,the impinging droplet,with a velocity ofU0and a certain impingement angle θi, is loaded into the calculation box.The angle between vertical line and the line connecting the center of the impinging droplet and the center of the footprint of the sessile droplet is set as θi,as shown in Fig.2.Time is normalized as τ=tσ/(μRc), wheretis the MDPD time.In order to make sure that the beginning moment of the collision process is the same for each run, the minimum distance between the surfaces of two types of particles is set to 1rc, and the simulation is initialized under this condition.More settings detail is shown in Table 1.It should be noted thatOhis varied with the liquid viscosity, and the liquid viscosity can be obtained by changing the friction coefficient γ.Micron droplets were chosen to lie within the operating parameters found in inkjet printing[13]and general medical spray[48].In a typical inkjet printing system, for example, the dropletvelocity is 5 m∙s-1and droplet viscosity is 10 mPa∙s [13].In this work, the droplet velocity is 3–6 m∙s-1and droplet viscosity is 6–10 mPa∙s.Thus, the range ofWehere is from 5.68 to 22.7, and the range ofOhhere is from 0.136 to 0.214.

Table 1Parameters setting in MDPD simulations

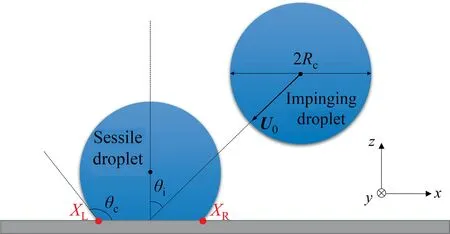
Fig.2. Schematic of an impinging droplet impact on a sessile droplet having contact angle θc at an impingement angle θi.

3.Results and Discussion

3.1.Droplet impingement behavior

In this section,we focus on the impingement of a droplet colliding with a sessile droplet under different impingement angles.The Weber number of the impinging droplet has been fixed to 22.7 and the Ohnesorge number to 0.136.The wetting property of the substrate are set as hydrophilic (θc=45°) or hydrophobic (θc=124°).

Impressions of the impingement process under the various conditions are shown in Fig.3.The momentum exchange between the liquid in the two coalescing drops gives rise to a moving threephase contact line.This has been quantified in Fig.4 that shows time series of the outer left and right points on the contact line as well as of the center of the drop’s footprint on the surface.Strong droplet deformations are observed for τ ≤20.During later period,deformations are much less.The hydrophobic merged droplet, however, keeps sliding in the negativex-direction over the surface until τ ≈100 for non-zero impingement angles as a result of the negativex-momentum of the incoming droplet (see Fig.4).The sliding distances for hydrophilic droplet are at least one order of magnitude less than the hydrophobic droplet due to the much stronger adhesion on the substrate.The head-on and small-angle collisions of the hydrophobic droplets give rise to oscillations of the three-phase contact line with a temporary retraction which is strongest at τ ≈20.

Fig.3. Snapshots of droplet (green) impingement on a sessile droplet (amber) at various impingement angles θi on (a) hydrophobic surface and (b) hydrophilic surface.

Further insight on the flow dynamics inside the droplet has been obtained by visualizing its velocity field, as done in Fig.5.For this we need the ensemble-average.If we take a single realization,the velocity field is overwhelmed by random thermal motion of the molecules (as in Fig.5(a)).For this reason, we repeat the impingement process 50 times, each with a different, statistically independent initial randomization.The result of the velocity field is shown in Fig.5(b).If we subtract the average velocity of the droplet we arrive at Fig.5(c)that shows that the impingement generates an internal recirculation in the hydrophobic droplet at τ ≈14.In Laietal.’s [24] experiment, they also found an internal recirculation pattern based on a micro-LIF measurement.

Fig.4. Time series of contact points (as defined in Fig.2) displacement of merged droplet on (a) hydrophobic surface and (b) hydrophilic surface.Xc=(XR + XL)/2.

Fig.5. (a–c) Velocity fields inside merged droplets on hydrophobic surface: (a) single realization, (b) ensemble averaged realization, (c) ensemble averaged velocity field relative to the average velocity of droplet v (, N the particle number in merged droplet).(d) and (e) Ensemble averaged velocity fields relative to the average velocity inside the merged droplets on a hydrophilic surface.The impingement angle (θi) equals 45°.

The velocity fields in the hydrophilic droplet (Fig.5(e) and (f))show a recirculation at short times (τ ≈5) but not anymore at τ ≈14.Apparently the stronger adhesion and smaller wall normal length scales of the hydrophilic droplet dissipate internal flow much faster as compared to the hydrophobic droplet.

3.2.Droplet mixing performance

The mixing of two miscible droplets is achieved through convective mass transfer (organized motion of molecules) and diffusive mass transfer (random motion of molecules).A common method to estimate the mixing performance experimentally in the stage of diffusive mass transfer is the mixing index (see Eq.(1)).Three-dimensional experimental evaluation of the convective stage is limited due to the limitation of sampling rate and concentration distribution reconstruction efficiency after a complete 3D scan [24].However, this drawback can be overcome in a simulation.

3.2.1.Dropletkineticenergy

First the mixing performance in the stage of convective mass transfer is evaluated by tracking the kinetic energy of the impinging droplet.The variation of scaled kinetic energy,together with the variation of the velocity of the impinging droplet in three directions is shown in Fig.6.Here, the kinetic energy of the impinging dropletEkis calculated as

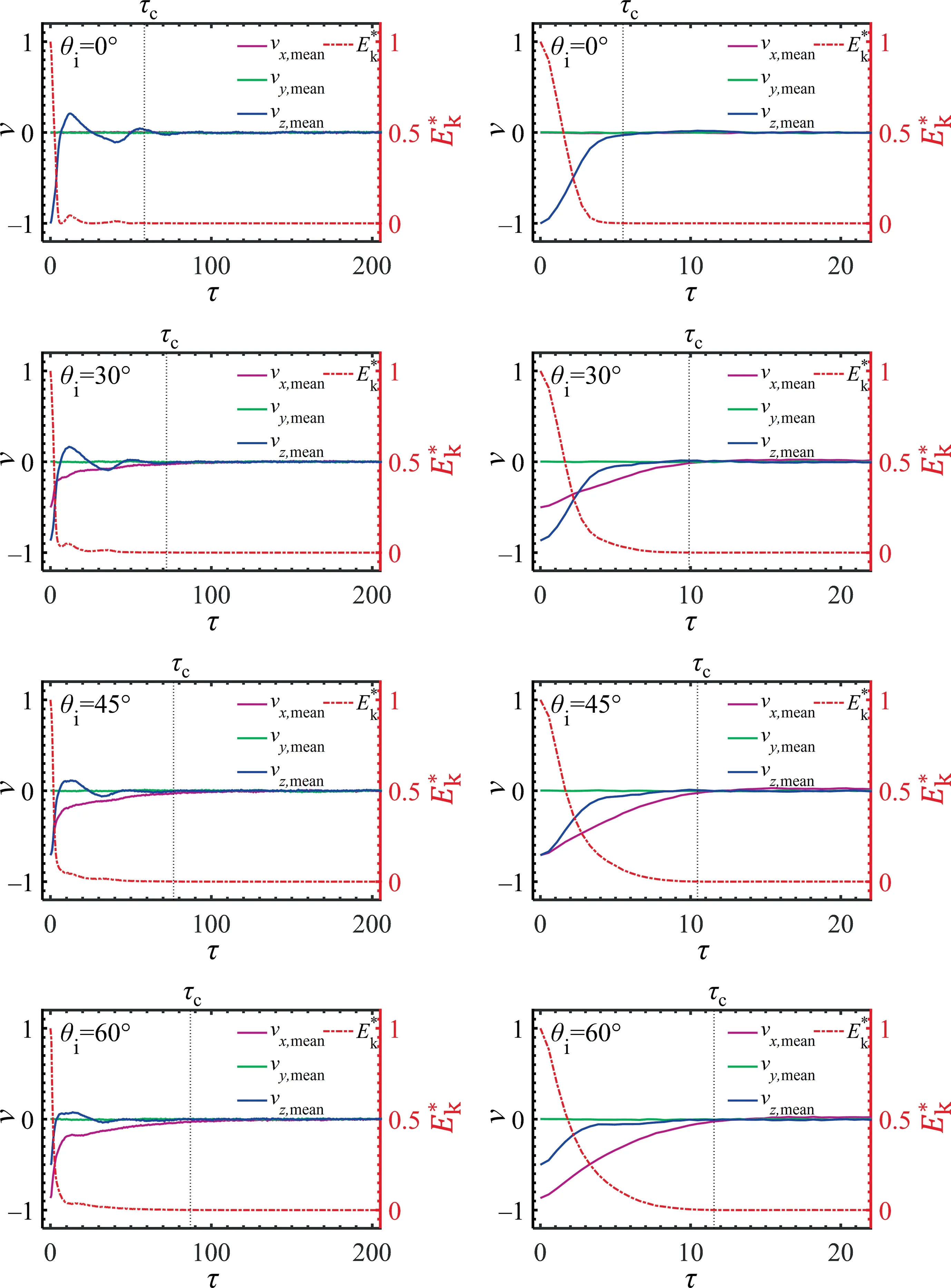
Fig.6. The mean velocity vmean and the scaled kinetic energy E*k of the impinging droplet as a function of time.τc indicate the when the E*k <0.001.Left hydrophobic, right hydrophilic.We=22.7, Oh=0.136.

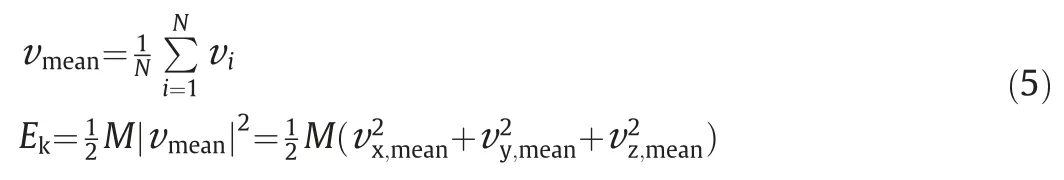
where,Nis the number of particles in the impinging droplet.And the scaled kinetic energy is defined as,whereis the initial kinetic energy of the impinging droplet with the velocity unity.

We assume that the convective mixing stage is finished when the kinetic energy of the impinging droplet is low enough, such as<10-3.We find that the value of τcin the case of hydrophobic surface are all larger than that in the case of hydrophilic surface.This is because the attraction between hydrophilic surface and liquid particles is larger than that between hydrophobic surface and liquid particles, and this attraction hinders convection in the droplet.Additionally, the value of τcincreases with θi.This is because of the increase of initial velocity in the horizontal direction vx,and the increased time required for the droplet to come to rest under the same surface condition.

The variation of droplet velocities can also indicate that there is diffusion of droplet particles.When collision happens,the particles in the impinging droplet move towards the sessile droplet as the velocities of impinging droplet decreases.The particle motion inydirection cannot be illuminated in Fig.6, since the collision is symmetric about thex–zplane, which results in the value of the mean velocity inydirection remains zero all the time.

3.2.2.Dropletinternalconcentrationfield

Fig.7 shows the mixing inside the merging droplets in terms of concentration contours of the liquid in the sessile droplet.The method to extract concentration distribution is shown in Fig.8.Firstly, a slice with the thickness of 1 on thex–zplane(y∊[-0.5, 0.5]) is extracted from the merged droplet (Fig.8(a)), and then this slice is divided into cubes with a side length of 1 (Fig.8(b)).By counting the number of particles belonging to the impinging and sessile droplet respectively, the concentration of the liquid originally belonging to the sessile droplet in this cube can be calculated.Finally, the instantaneous concentration field in the merged droplet can be obtained by averaging 50 cases with different random seeds.Here, the local mixing is illustrated by the variation of concentration of sessile droplet,C1; a value of 0.5 implies a full mixing, whereasC1=0 orC1=1 indicates complete segregation.

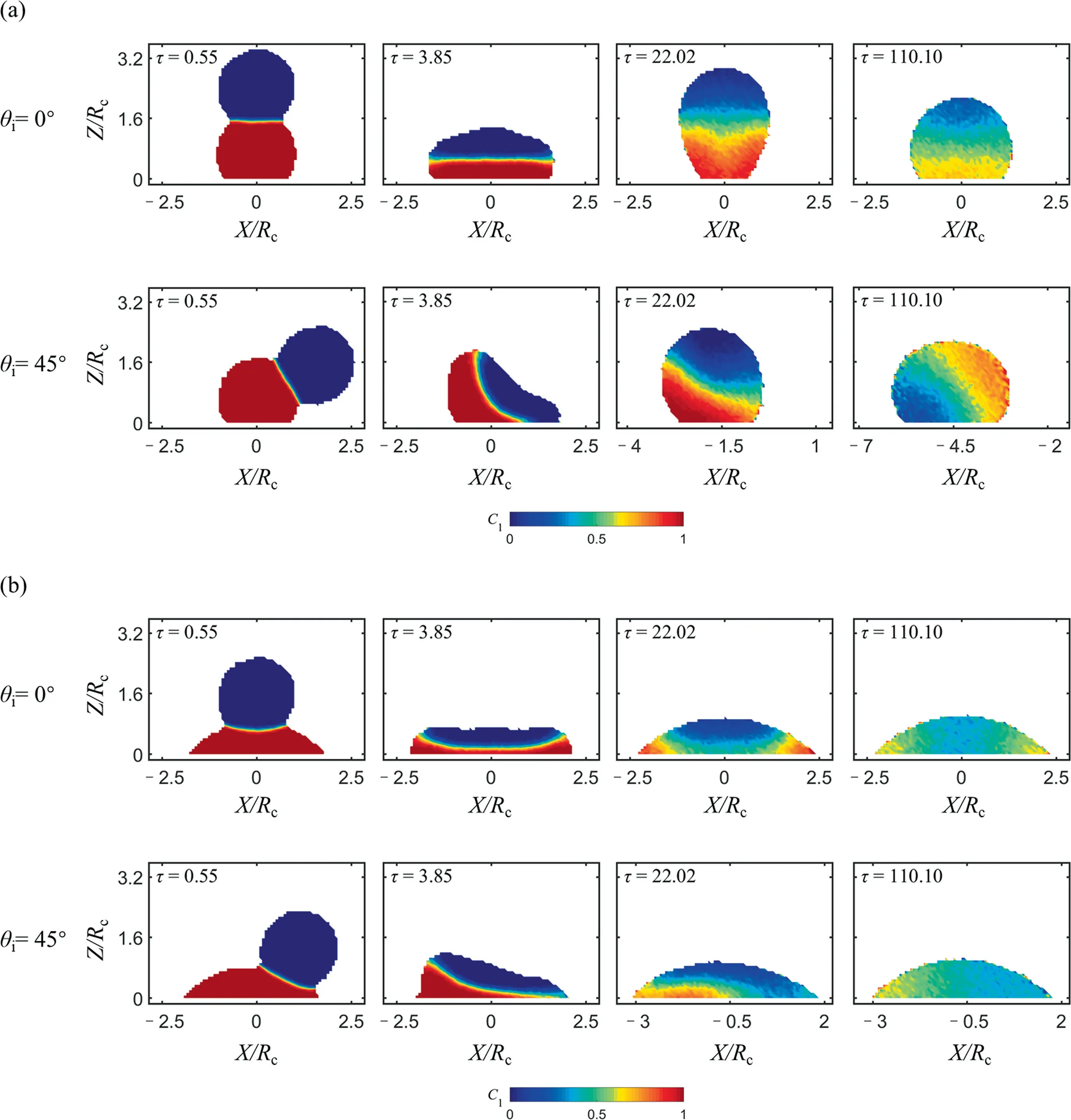
Fig.7. The instantaneous concentrations of sessile droplet on (a) hydrophobic surface and (b) hydrophilic surface.We=22.7, Oh=0.136.

Fig.8. Schematic diagrams of calculation method of concentration profile field in a cross section of the merged droplet.

At the beginning of droplets contact, the interface is welldefined (τ=0.55).After some time (τ=3.85–110.10), the interface becomes indistinct and the mixed area (C1≈0.5) increases around the interface as a result of diffusion.This phenomenon can be observed under various conditions, see Fig.7.For headon collision, the mixed area appears in the middle for hydrophobic surface with the liquid particles diffusing upwards and downwards; whereas for hydrophilic surface the liquid particles diffuse radially.For the asymmetric collision, the mixed area also is asymmetric, where the leading part of sessile droplet and trailing part of impinging droplet are still unmixed (τ=22.02).In addition, we can see that the concentration gradient direction in the merged hydrophobic droplet is reversed between the moments τ=22.02 and τ=110.10 when θiis 45°, which is because that the merged droplet is ‘‘rolling up” on the hydrophobic surface and the impinging droplet gradually becomes a part of the leading edge (Fig.3(a), θi=45°, τ=22.0 2–110.10).From Fig.7, we also can find that the droplet is still not fully mixed when the convective mixing stage is over.

3.2.3.Totalmixingtime

The total mixing time of two droplets are indicated by themixingfunction proposed by Paketal.[34],based on the distribution of liquid molecules in 3D space:

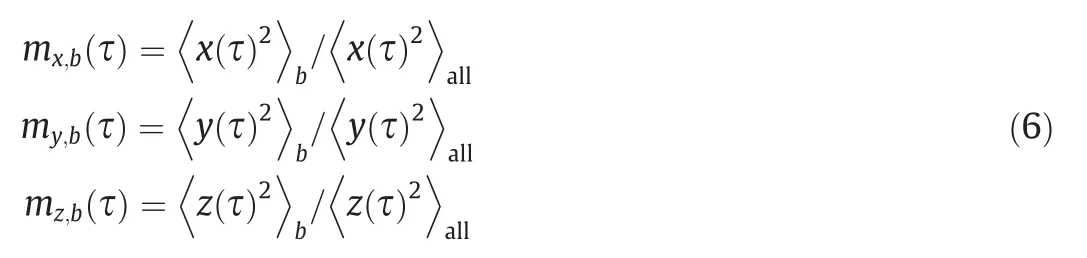
Here,bis the sessile droplet part (S) or impinging droplet part(I), and ‘‘all” represents the merged droplet part.By calculating the average of the square of particle coordinates (, and) in three dimensions, the particles can be regarded as completely mixed when themx,b(τ)=my,b(τ)=mz,b(τ)=1.When calculating the value ofm(τ), we take the center of the footprint of the sessile droplet as the origin of the coordinate system.

The variation ofm(τ)with time is plotted in Fig.9.For head-on collision, the change ofmx(τ) andmy(τ) with time are the same,indicating – as expected – the same mixing rate in bothxandydirection.For θi> 0 cases, the values ofmx(τ) andmz(τ) decline rapidly(τ=0 to τ=10)due to the quick movement of the particles from impinging droplet to sessile droplet as soon as the collision begins.

Fig.9. Mixing progress of the droplets on hydrophobic surface (left column) and hydrophilic surface (right column) expressed in terms of the m(τ) functions.We=22.7,Oh=0.136.Since m(τ) cannot exactly become equal to one, we obtained τc when |1 - m(τ)| ≤0.01.

Additionally,we also learn that the droplets are not fully mixed at the end of the convective stage,since them(τ)does not stabilize at 1 after τ reaches τc(τcis shown in Fig.6).It still takes more time to reach full mixing,and after τcthe molecular diffusion dominates the mixing process.

The dimensionless total mixing time of the droplet for differentWeandOhcombinations is plotted in Fig.10(a),whereWeis varied by changing the droplet velocityU0(see Fig.2)andOhis varied by changing the droplet viscosity μ.We can see thatWeandOhhardly have an effect on τm.The mixing time of hydrophobic droplets is smaller than hydrophilic droplets, and the mixing time increases as θiincreases on a hydrophilic surface.

Fig.10. (a)Total mixing time,(b)flow time of the droplets under different conditions and(c)diffusion time of the droplets derived by total mixing time minus flow time.The hollow bar with black frame is the estimation value, and the error bar represents the standard deviation.

3.2.4.Convectivetimeanddiffusiontime

In order to interpret the difference of τmunder various conditions,the convective time(τc)and the diffusion time(τd)are calculated respectively.As shown in Fig.10(b) and (c), we can see that the influence ofWeandOhon τcis not as great as that of surface wettability.Besides, larger θiresults in a longer τc, indicating that the internal recirculation lasts longer and fluid disperses vertically and horizontally.It is reported that this internal recirculation can benefit mixing [24].However, in this work, we find that a longer τcdoes not lead to a shorter total mixing time.This is because in this mixing process,τcis one order of magnitude smaller than τd,which means the total mixing time is dominated by diffusion.However, the convection eventually does determine the initial state of the diffusion process as shown in Fig.11, which then affects the total mixing time.

We estimated τdby the squared diffusion length divided by self-diffusion coefficient, where the self-diffusion coefficient (D)can be determined through the Einstein equation [50]:

where the mean-square-displacement of the freely diffusing particle along the time (MSD(t)) can be written as

where ri(t)-ri(0)is the vector distance traveled by a given particle over the time interval.From this method, for example, for the caseOh=0.136,we can get the self-diffusion coefficientDis 0.0615;and for the caseOh=0.214, the diffusion coefficientDis 0.039.

Diffusion distance, which is related to the concentration distribution in the bulk,is another important factor determining the diffusion time.In order to determine the diffusion distance,we count the percentage of particles in the concentration range of 0 to 1.0 for each case at the end of the convection stage, seen in Fig.12 as an example.In the figure, two concentration peaks occur atC1=0.2 andC1=0.85, respectively, which means most particles are in the concentration ofC1=0.2 and ofC1=0.85.Therefore,these two values can be regarded presenting the bulk concentration for the corresponding case,and the diffusion distance(df)is defined as half of the distance marked by dashed line pieces in the panel of Fig.11.

Fig.11. The determination of diffusion length on (a–d) hydrophobic surface and on (e–h) hydrophilic surface when Oh=0.136, We=22.7, after convective stage is over.A dash line represents one distance from the main high concentration location to the main low concentration location,where the main high concentration location and main low concentration location is dependent on the concentration distribution (see Fig.12).And this distance equals twice the diffusion distance df.

For the hydrophilic cases we notice that the horizontal concentration gradients largely exist in the near wall layer when θi≥45°.And in these cases, when we count the percentage of particles in the concentration range, only the particles closed to the surface(within 0.5rc) are considered.

The estimated diffusion time are shown in Fig.10(c)in bar with black frame.Comparing with the diffusion time calculated by the total mixing time minus flow time, the trend of the diffusion time along the impinging angle has been captured.Since we consider the diffusion distance as the distance over a concentration difference of the majority of particles,a small part of particle whose diffusion distance larger than majority’s has not been considered,which results in the underestimation of diffusion time in some cases.

In addition, the dimensionless Pelect number (Pe) is usually used to describe the competition between convection and diffusion.We can obtain the dropletPebyPe=(Rcthe initial radius of the impinging droplet, vmeanthe average velocity of impinging droplet andDthe diffusion coefficient of the liquid particles) and find thePedecays from ～200 at the very beginning of mixing to ～O(100) at τc(when the convection and diffusion have approximately equal time scales), that is to say, the convection dominates the mixing when τ<τcand then the importance of diffusive mass transfer cannot be ignored thereafter.It can also be regarded that the method distinguishing the convection stage and diffusion stage by the decay of the kinetic energy of the impinging droplet is reasonable.

We can conclude that the θiand surface wettability affect the droplet concentration distribution at the start of the diffusion stage.And the concentration distribution then affectsdf.For hydrophobic surface, although the concentration distribution is different under different θicases,dfshows little difference.For hydrophilic surface,however,dfincreases with θi,and the increasedfresults in an increase τd.Compared to a hydrophilic droplet, a hydrophobic droplet has a smallerdf.To sum up, the mixing time can be shortened by reducing the imping angle and applying the hydrophobic surface due to the smaller diffusion distance.

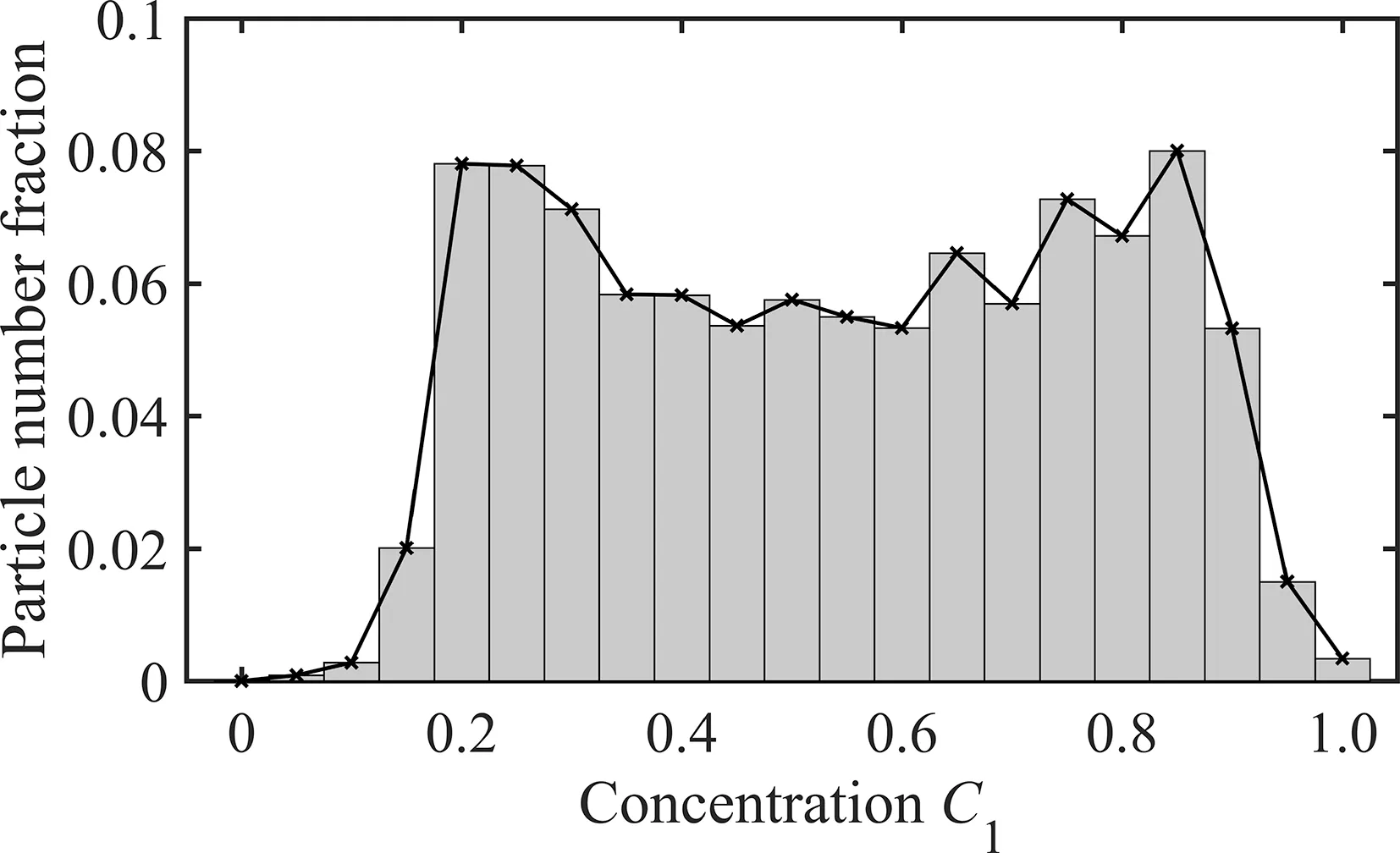
Fig.12. The particle number fraction over a range of concentrations for the case(θc=124°, θi=30°, Oh=0.136, We=22.7).The concentration interval is 0.05.The largest particle number fraction occurs at C1=0.85 if C1>0.5 and C1=0.2 if C1<0.5.

4.Conclusions

Mixing between droplets on the solid surface induced by impingement is a common phenomenon in process industry.By means of a particle-based simulation method,many-body dissipative particle dynamics(MDPD),this process is investigated in order to realize how it is affected by the properties of droplets and solid surface, and droplets operation conditions.

Impingement angle and the surface wettability can both affect the motion of droplets on the solid surface,where there is a larger migration displacement along with larger impingement angle,and the merged droplet travel further on hydrophobic surface than that on the hydrophilic surface.In addition, an internal recirculation is found inside the merged droplet during the impingement process.

In terms of mixing time, it can be determined by the modifiedmixingfunction.By changing the dimensionless numbers of dropletWeandOhcan hardly affect the dimensionless mixing time (τm).However,the value of τmis sensitive to the properties of solid surface,and a larger impingement angle will lead to a larger τmon the hydrophilic surface,while the impingement angle can hardly affect τmon the hydrophobic surface.

The whole process of mixing can be divided into convection dominant and diffusion dominant stages, quantitatively according to the droplet kinetic energy.Generally,the duration of convection dominant stage is much shorter than that of diffusion dominant stage.The concentration distribution inside the merged droplet can be an important factor determining the diffusion distance,which will further affect the diffusion time.The diffusion distance of hydrophilic droplets is larger than that of hydrophobic droplets,and is dependent on the impingement angle.Therefore,in order to shorten the mixing time between impinging droplets on hydrophilic surface,reducing the impingement angle is an effective way,for example, by choosing a proper spraying nozzle and reducing the spray angle in the application of sprayable drugs for post-surgical cancer treatment [35].

This work only concentrates on the droplet impingement and mixing on a homogeneous solid surface.But inhomogeneous surfaces are common in practical work, in the future the droplets impinging and mixing on inhomogeneous surface can be a potential direction.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors gratefully acknowledge the financial support from National Natural Science Foundation of China (22078008,22178014) and the Fundamental Research Funds for the Central Universities (XK1802-1).