基于分形理论和扩展有限元法的钢纤维混凝土损伤破坏机理

王辉明，李汝飞，邓平贵

(新疆大学建筑工程学院，乌鲁木齐 830017)

0 引 言

钢纤维混凝土(steel fiber reinforced concrete， SFRC)是由乱向分布的钢纤维、粗细骨料、砂浆等组成的多相非均质复合材料，具有良好的受拉、受弯和受剪性能。有研究[1]发现只需掺入0.5%～1.5%(体积分数)的钢纤维就可使SFRC的抗压强度、抗拉强度和抗折强度分别提高5.41%～32.87%、24.02%～29.90%和7.33%～40.07%，故其在工业与民用建筑、机场、高速公路、特种结构等领域得到了广泛应用。大量工程灾害表明，混凝土结构的破坏往往是其内部裂纹扩展和损伤积累所导致的。因此，对SFRC损伤演化和裂纹扩展进行研究是很有必要的。SFRC的损伤本质上是其内部细观微缺陷在荷载、温度等外部因素作用下不断萌生、扩展、交叉、融汇、贯通成为宏观主裂缝的过程，从而在宏观上表现出本构关系的非线性和力学性能的劣化等行为。SFRC承载能力丧失只是裂纹发展的最后阶段，只能在很小程度上揭露损伤演化的历史和特征，要想真正描述混凝土破坏的非线性特征，必须追溯到初始裂纹分布、裂纹扩展和损伤演化过程，从微裂纹动态演化和材料损伤的角度出发，寻找演化机理及失稳破坏的依据[2]。但是，复杂的外界条件及SFRC自身的非线性特征使裂纹的动态演化规律研究变得十分困难。

随着科学技术的不断发展，声发射、计算机层析扫描(computed tomography, CT)、数字图像相关(digital image correlation, DIC)等技术为混凝土的裂纹发展研究提供了新的方式。李杰等[3]研究了混凝土破裂过程中伴随的声发射现象，通过建立混凝土破裂过程中内部结构状态变化(损伤演化)和声发射特征的对应关系，揭示了混凝土的变形破坏由渐变性发展到突变性。方建银等[4]基于CT技术研究了混凝土试件静、动力单轴拉伸和压缩破坏过程中的裂纹演化规律和强度特征。雷冬等[5]运用DIC技术对混凝土材料表面损伤应变场进行了测量。上述方法虽然可以有效研究混凝土的裂纹发展和损伤演化过程，但声发射过程常伴随着噪音干扰，结果容易受去噪方式的影响，难以将细观破坏定量化；CT技术只是对不同层位CT图像或剖面图像的裂纹进行统计，并不能全面反映裂缝的空间分布状态，且试验结果因受扫描断面和扫描次数的影响表现出离散性；DIC技术则着重关注试件表面变形前后的散斑图像，无法捕捉其内部变形特征，不能全面反映试件变形特征。分形理论的提出为混凝土的损伤破坏研究提供了新的视角，很快在微细观结构及其受力变形特性等方面得到了广泛应用。谢和平院士最早将分形理论引入岩石和混凝土研究，现阶段分形理论在混凝土研究方面的应用主要包括：一是以分形骨料级配为变量对混凝土配合比设计进行研究；二是对混凝土裂纹的产生和发展过程进行分形计量和表征。李国强等[6]首次应用分形理论，通过分析路面材料骨料级配分形行为推导出骨料的分形级配公式。于江等[7]进行了混凝土梁四点弯曲试验，并将提取到的梁表面裂纹进行分形计算，研究裂纹分形维数与再生骨料取代率的联系。赵志浩等[8]进行了钢筋混凝土梁的受剪试验，并用计盒维数法分形处理梁的表面裂纹，研究剪跨比和箍筋配筋率对裂纹分形特征的影响。已有研究表明，裂纹分形维数可以很好地描述混凝土受力过程中裂纹和损伤的演化过程。在混凝土损伤破坏过程中，随着裂纹的产生和扩展，有限元等传统数值方法往往需要重新生成网格，这不仅工作量巨大,还会因为网格扭曲等问题造成计算过程不收敛。扩展有限元法(extended finite element method， XFEM)在模拟界面、裂纹生长等不连续问题时具有明显优势[9]，能够克服传统有限元法在诸如裂纹尖端等高应力和变形集中区进行高密度网格划分所带来的困难，模拟裂纹扩展时无需重新生成网格，因此在研究混凝土裂纹发展方面得到了广泛应用[10-11]。

目前，国内外对钢纤维混凝土的损伤破坏研究多数是通过试验方法探讨钢纤维对混凝土强度、韧性等宏观力学性能的影响，而从细观层次研究钢纤维混凝土损伤破坏的工作相对较少。为了更深入、更全面地研究钢纤维混凝土裂纹发展及损伤演化过程，本文以分形理论和扩展有限元法为基础，采用基于裂纹分形维数计算得到的损伤值对混凝土开裂全过程的裂纹分布进行表征，同时利用扩展有限元法在模拟裂纹扩展时无需对网格进行重新生成的优势，对SFRC的裂纹发展和损伤演化过程进行研究，并以钢纤维体积掺量和长度、骨料形状等重要因素为考察因素，研究其对SFRC损伤演化过程的影响。加深对宏观尺度上钢纤维混凝土力学行为的理解，以期能够更科学合理地描述材料的破坏和失效过程，更准确地模拟和预测材料的力学行为，推动科学研究的发展，实现工程结构的精细化设计和控制，最大程度降低安全风险和经济成本。

1 分形理论和扩展有限元的基本概念及公式

1.1 基于裂纹分形维数的损伤值

分形(fractal)是数学家Mandelbrot基于自相似性(一个几何对象局部放大后与其整体相似的性质)提出的，具有以非整数维形式填充空间的形态特征。通过引入分形维数的概念，将分形用数值表示。分形维数是传统维数(整数维)概念的推广，是一种度量自然界中复杂形态的新方法。分形维数的计算方法有多种，如Hausdorff维数、相似维数、拓扑维数、计盒维数等。

本文利用计盒维数对混凝土裂纹进行研究，其思想是用边长为r的nd维立方体(盒子)来覆盖研究对象，并得到不同边长值r对应的盒子数N(r)，然后在以ln(1/r)为横坐标、lnN(r)为纵坐标的双对数坐标系中得出不同的点(ln(1/r),lnN(r))，最后采用最小二乘法拟合得到的直线斜率即为计盒维数，其计算公式如式(1)所示。

(1)

式中：F为裂纹分布的计盒维数；r为盒子的边长，以1/rk变化(k=0，1，2，…)；N为用边长为r的盒子去覆盖裂纹所需的盒子数。

(2)

式中：Fi、Fj分别代表第i和第j个分析步的裂纹分形维数；n为模拟所需的总分析步数，且m≤n。

1.2 扩展有限元

扩展有限元法是1999年美国西北大学Belytschko等[13]为解决裂纹扩展问题而提出的，其核心思想是改进带有不连续性质的形函数来反映区域间的间断，在计算过程中，不连续场的描述完全独立于网格边界，在处理断裂问题方面有较好的优越性。扩展有限元裂纹网格如图1所示。增强的形函数包括捕捉裂纹尖端奇异性的裂尖渐近函数和表示裂纹表面位移跳跃的阶跃函数，见公式(3)。

(3)

图1 扩展有限元裂纹网格Fig.1 Extended finite element crack mesh

阶跃函数H(x)用来反映裂纹面不连续的特性，其具体表达式如式(4)所示。

(4)

裂尖渐进函数Fα(x)用于反映裂纹尖端位移场的不连续性，是以裂尖为原点的极坐标系进行表示，设置裂尖切线方向θ=0，由四个基函数组成，其表达式如式(5)所示。

(5)

常采用水平集法(level set method， LSM)来描述裂纹的增长。用LSM表示裂缝和裂尖的位置，用扩展有限元法计算裂纹扩展速率所需的应力和位移场。

2 模型的建立与验证

2.1 混凝土立方体试件抗拉细观模拟

基于文献[14-16]和蒙特卡洛方法建立混凝土立方体试件二维细观模型，骨料的体积分数为46.9%，试件尺寸为150 mm×150 mm，圆形骨料粒径分布范围为10～28 mm。考虑到二维混凝土细观模型的网格划分、计算效率及收敛问题，本文模拟不考虑界面过渡区厚度，认为钢纤维混凝土细观模型由骨料、钢纤维、砂浆三相组成，即认为界面过渡区与砂浆的力学性能基本一致，参考文献[14]，抗拉强度取3.37 MPa，断裂能取0.161 76 N/mm。采用ABAQUS程序进行有限元分析，骨料、砂浆采用四节点平面应力单元(CPS4)，钢纤维采用二节点桁架单元(T2D2)，各组分材料参数[14]见表1，破坏准则选用最大拉应力准则。生成的细观有限元模型如图2(a)所示，试件下边界受到竖直方向的面约束和水平方向的点约束，两侧不受任何约束，试件上边界采用位移加载方式。

表1 各组分材料参数[14]Table 1 Material parameters of each component[14]

图2 素混凝土立方体试件细观有限元模型及破坏图Fig.2 Mesoscopic finite element model and failure diagrams of plain concrete cube specimens

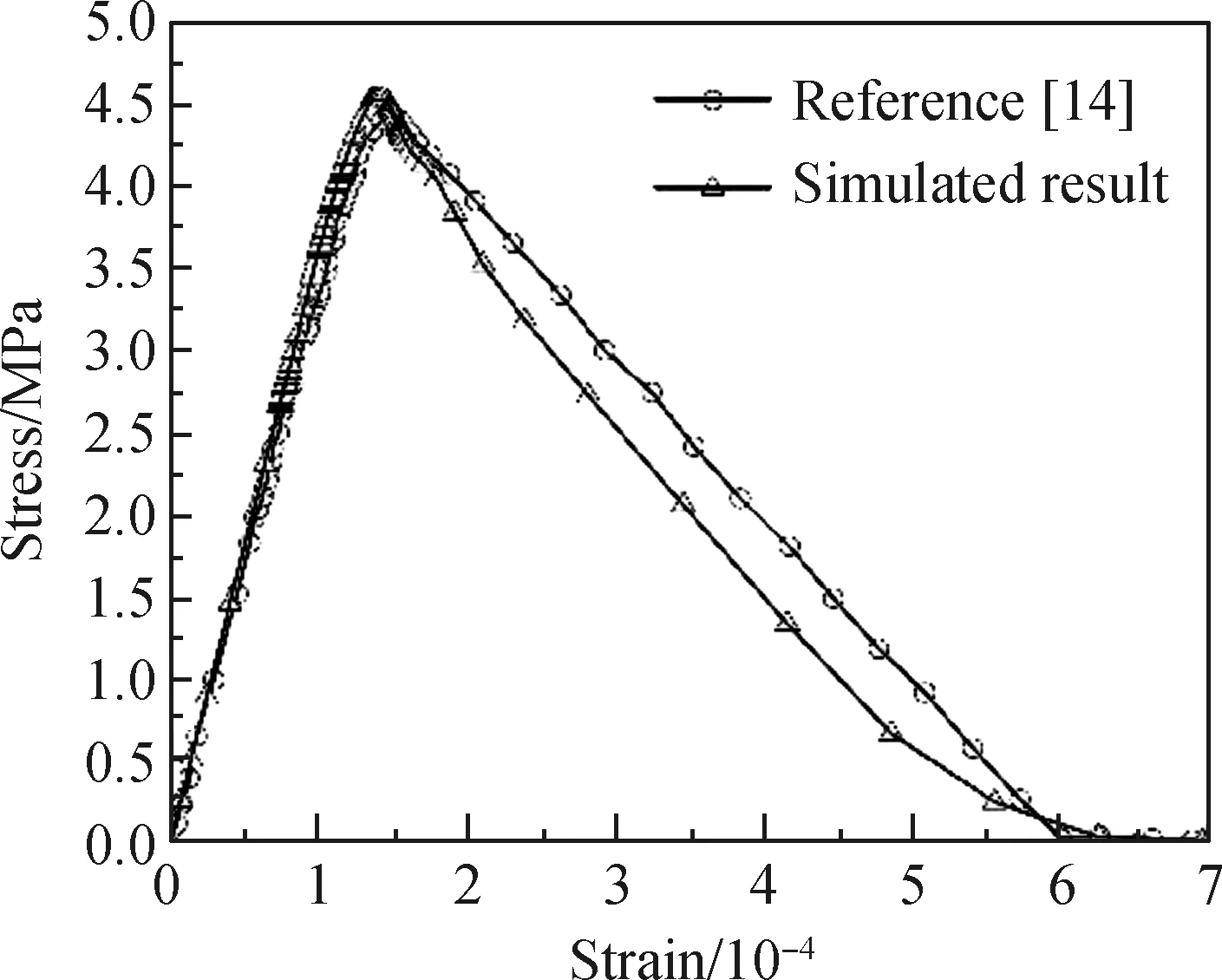
图3 素混凝土立方体试件受拉应力-应变曲线Fig.3 Tensile stress-strain curves of plain concrete cube specimens

本文数值模拟得到的混凝土立方体最终受拉破坏现象(见图2(b))与文献[14]的受拉破坏现象(见图2(c))相符。图3是本文数值模拟和文献[14]的素混凝土立方体试件受拉应力-应变曲线对比图，可知，本文的二相(骨料和砂浆)素混凝土立方体抗拉强度为4.53 MPa，与文献[14]采用三相(骨料、砂浆和界面)模型的抗拉强度(4.43 MPa)误差为2.26%，小于5%，且二者曲线吻合较好，说明本文的细观有限元模型具有良好的准确性。

2.2 切口梁三点弯曲试验裂纹扩展模拟

参考文献[17]的切口梁三点弯曲试验建立宏观有限元模型，切口梁试件尺寸见图4，混凝土参数见表2。切口梁的尺寸为1 000 mm×200 mm×120 mm，预设裂纹长度为80 mm，跨中受集中力作用。为更精确地模拟裂纹的扩展和演化，以预制裂纹为中心划分为3个区域，中间区域采用高密度网格划分，两侧区域采用较粗的网格划分，整个区域均采用四节点平面应力单元(CPS4)，破坏准则选用最大拉应力准则。

表2 混凝土及材料参数Table 2 Concrete and material parameters

本文得到的荷载-裂缝张开口位移(F-CMOD)曲线与文献[17]的试验曲线对比如图5所示，切口梁抗折强度峰值为4.316 kN，与试验值4.426 kN误差为2.49%，小于5%，且二者曲线吻合较好。本文二维模拟得到的最终破坏现象如图6(a)所示，与文献[17]三维模拟的最终破坏现象(见图6(b))相一致，说明本文的二维宏观有限元模型具有足够的可靠性。

图4 切口梁试件尺寸Fig.4 Size of notched beam specimen

图5 素混凝土切口梁荷载-裂缝张开口位移曲线Fig.5 F-CMOD curves of plain concrete notched beams

图6 素混凝土切口梁破坏图Fig.6 Damage diagrams of plain concrete notched beams

3 参数化分析

以上述混凝土立方体无预制裂纹抗拉试验和切口梁三点弯曲试验数值模拟与相关试验测试结果比较验证为基础，本节探究钢纤维掺量和长度等重要参数变化对钢纤维混凝土损伤演化过程的影响。

3.1 SFRC立方体抗拉试验损伤破坏分析

以钢纤维体积掺量(0%、0.5%、1.0%)、钢纤维长度(25 mm、35 mm、45 mm)和骨料形状(圆形、椭圆形、多边形)为考察变量，研究其对SFRC立方体抗拉强度及裂纹损伤演化过程的影响。

3.1.1 钢纤维掺量的影响

选取截面直径为0.55 mm、长度为35 mm的平直型钢纤维，并参考文献[18-19]给出的方法计算钢纤维数目，可得不同钢纤维掺量的SFRC细观有限元模型，如图7所示。

图8为钢纤维体积掺量为0.5%的混凝土立方体受拉过程中不同分析步下的裂纹发展图，根据计盒维数和损伤值的计算方法，可得如表3所示的各分析步对应裂纹的分形维数和基于裂纹分形维数的损伤值，将应力、裂纹分形维数、损伤值与应变的对应关系由3Y轴图表示，代表素混凝土立方体受拉损伤过程。根据相同方法计算钢纤维体积掺量为0%和1.0%的SFRC各分析步对应裂纹的分形维数和基于裂纹分形维数的损伤值，绘制3Y轴图，如图9所示。

图7 不同钢纤维体积掺量的SFRC细观有限元模型Fig.7 Mesoscopic finite element model of SFRC with different steel fiber volume content

图8 钢纤维混凝土立方体受拉裂纹发展图(钢纤维体积掺量为0.5%)Fig.8 Development diagrams of tensile crack of SFRC cube (steel fiber volume content is 0.5%)

从图9可知,钢纤维体积掺量为0.5%和1.0%的SFRC立方体抗拉强度分别为5.09 MPa和5.43 MPa，相较于素混凝土的立方体抗拉强度4.53 MPa分别提高了12.4%和19.9%，且相应的峰值应变也随着掺量的增加而增大。当钢纤维体积掺量为0.5%时，裂纹分形维数趋于平稳的时刻(此时刻之前，裂纹的分形维数变化明显，说明裂纹损伤路径在不断发展；此时刻之后，裂纹的分形维数趋于平稳，说明裂纹损伤演化的路径基本形成，如图8(f)所示)，混凝土应力值刚好达到峰值，损伤值为0.944。随着钢纤维掺量的增加，裂纹分形维数趋于平稳的时刻相较于SFRC的应力峰值点不断提前，说明在裂纹分形维数趋于平稳(裂纹损伤路径基本形成)后的阶段，SFRC的力学性能不会立即退化。这是由于此阶段钢纤维与混凝土基体间的桥接作用(钢纤维和混凝土基质间的粘结力和摩擦力)在承受拉应力，减缓了SFRC的损伤破坏过程。从损伤值曲线也可看出，损伤值随着钢纤维掺量的增加而减小。

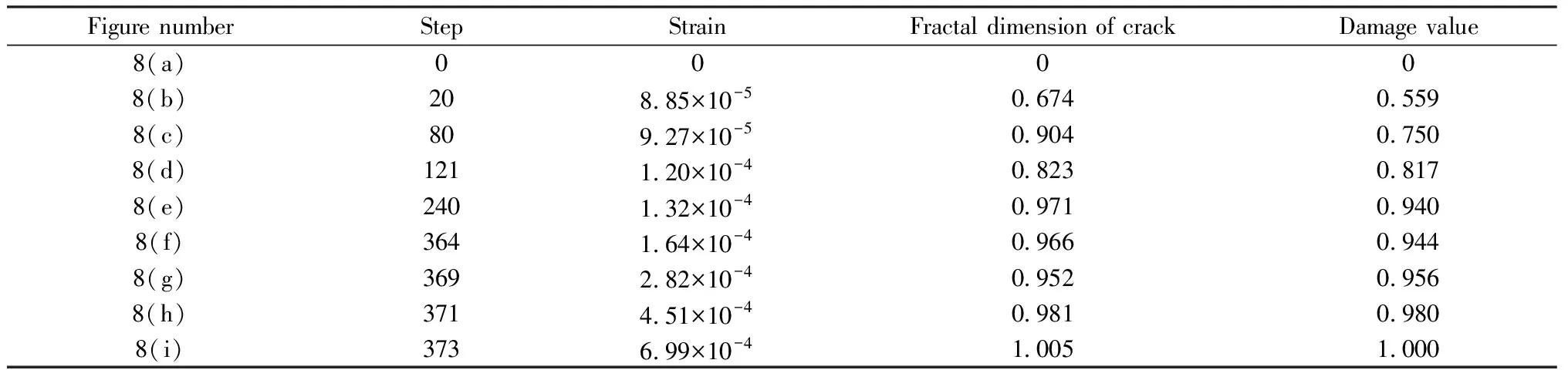
表3 损伤发展过程中各分析步对应的参数值Table 3 Parameter values corresponding to each analysis step in the damage development process

图9 不同钢纤维体积掺量的SFRC立方体损伤过程Fig.9 Damage process of SFRC cubes with different steel fiber volume content

3.1.2 钢纤维长度的影响

以0.5%体积掺量的钢纤维(截面直径为0.55 mm、长度为35 mm的平直型钢纤维)为基准，钢纤维长度分别取25 mm、35 mm、45 mm。按上述建模方法可得不同钢纤维长度的SFRC细观有限元模型，如图10所示。

图10 不同钢纤维长度的SFRC细观有限元模型Fig.10 Mesoscopic finite element model of SFRC with different steel fiber lengths

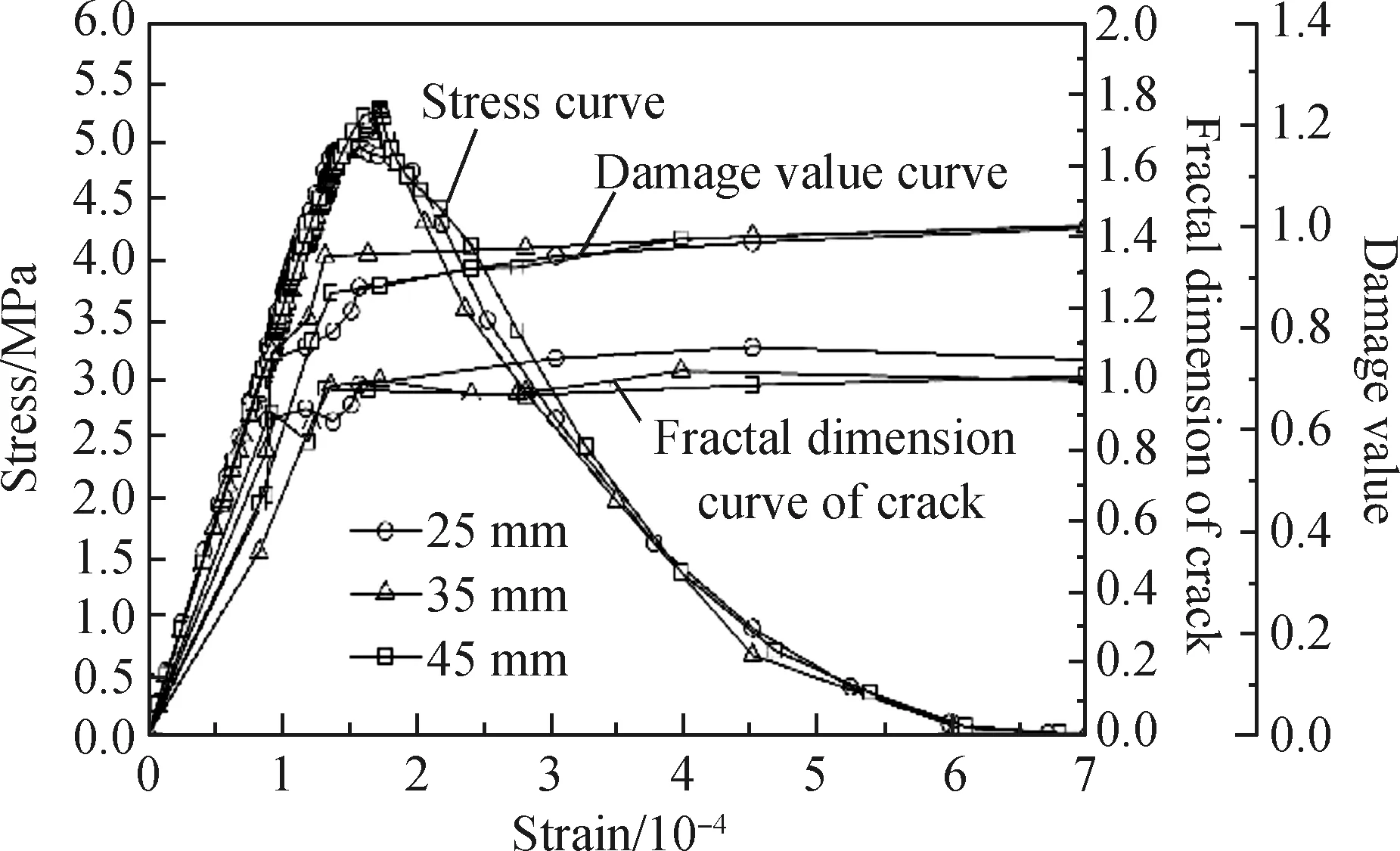
图11 不同钢纤维长度的SFRC立方体损伤过程Fig.11 Damage process of SFRC cubes with different steel fiber lengths

根据上述分形维数和损伤值的计算方法，得到不同钢纤维长度的SFRC各分析步对应的裂纹分形维数和基于裂纹分形维数的损伤值，将其绘制为3Y轴图，如图11所示。

由图11可知，钢纤维长度为35 mm和45 mm的SFRC的立方体抗拉强度分别为5.09 MPa和5.27 MPa，相较于钢纤维长度为25 mm的SFRC的立方体抗拉强度4.94 MPa分别提高了3.0%和6.7%，且相应的峰值应变也随着钢纤维长度的增加而增大。随着钢纤维长度的增加，裂纹分形维数趋于平稳的时刻相较于SFRC的应力峰值点不断提前，SFRC的损伤破坏过程得到延缓。这是因为随着钢纤维长度的增加，钢纤维与混凝土基体的粘结力和摩擦力增大，桥接作用增强，延缓了SFRC的损伤演化。

3.1.3 骨料形状的影响

以圆形骨料、0.5%体积掺量的钢纤维(截面直径为0.55 mm、长度为35 mm的平直型钢纤维)为基准，骨料形状取椭圆形和不规则多边形，分别表示卵石和碎石，按照与圆形骨料总面积相等的原则，换算成相应数量的椭圆形骨料以及不规则多边形骨料，研究骨料形状对SFRC立方体抗拉强度和裂纹损伤演化的影响。按上述建模方法可得不同骨料形状的SFRC细观有限元模型，如图12所示。

根据上述分形维数和损伤值的计算方法，得到不同骨料形状的SFRC各分析步对应的裂纹分形维数和基于裂纹分形维数的损伤值，将其绘制为3Y轴图，如图13所示。

图12 不同骨料形状的SFRC细观有限元模型Fig.12 Mesoscopic finite element model of SFRC with different aggregate shapes

图13 不同骨料形状的SFRC立方体损伤过程Fig.13 Damage process of SFRC cubes with different aggregate shapes

由图13可知，采用椭圆形和不规则多边形骨料的SFRC的立方体抗拉强度分别为5.19 MPa和5.24 MPa。相较于采用圆形骨料的SFRC的立方体抗拉强度5.09 MPa分别提高了2.0%和2.9%，且峰值应变均大于采用圆形骨料的SFRC。采用椭圆形和不规则多边形骨料的SFRC，其裂纹分形维数趋于平缓的时刻均早于采用圆形骨料的SFRC，说明SFRC的损伤破坏得到了延缓。这是因为采用椭圆形和不规则多边形的骨料，相较于圆形骨料，骨料界面增加，而裂纹萌生和发展均发生在薄弱的界面部位，骨料界面的增加，使SFRC的整体破坏路径增多，裂纹的扩展路径增多，则裂纹发展所需的能量亦增加，从而减缓了SFRC的损伤破坏过程。

3.2 SFRC切口梁三点弯曲试验损伤破坏分析

以钢纤维体积掺量(0%、0.5%、1.0%)、预设裂纹缝高比(0.3、0.4、0.5)和预制裂纹位置(距跨中0 mm、50 mm、100 mm)为变量，研究其对SFRC切口梁抗折失效荷载及裂纹损伤演化过程的影响。

3.2.1 钢纤维掺量的影响

钢纤维尺寸、类型均与前述相同，图14为钢纤维体积掺量为0%的切口梁抗折过程中不同分析步下的裂纹发展图，根据计盒维数和损伤值的计算方法，可得如表4所示各分析步对应的裂纹分形维数和基于裂纹分形维数的损伤值，将应力、裂纹分形维数、损伤值与应变的对应关系由3Y轴图表示，代表素混凝土切口梁抗折损伤过程。根据相同方法计算钢纤维体积掺量为0.5%和1.0%的SFRC各分析步对应裂纹的分形维数和基于裂纹分形维数的损伤值，绘制3Y轴图，如图15所示。

图14 素混凝土切口梁抗折裂纹发展图Fig.14 Development diagrams of flexural crack of plain concrete notched beams

由图15可知,钢纤维体积掺量为0.5%和1.0%的SFRC切口梁抗折强度分别为4.801 kN和5.345 kN，相较于钢纤维体积掺量为0%的SFRC切口梁抗折强度4.316 kN分别提高了11.2%和23.8%，说明钢纤维掺量的增加可以提高切口梁的抗折强度。由裂纹分形维数曲线和损伤值曲线可知，随着钢纤维掺量的增加，SFRC切口梁损伤破坏过程得到了较小程度的延缓，这是因为钢纤维在混凝土基体中是乱向随机分布的，并不都集中在预制裂缝附近，在裂纹扩展路径基本形成后，不同掺量下的钢纤维桥接作用相差不大，从而SFRC切口梁的损伤演化过程得到较小程度的延缓。

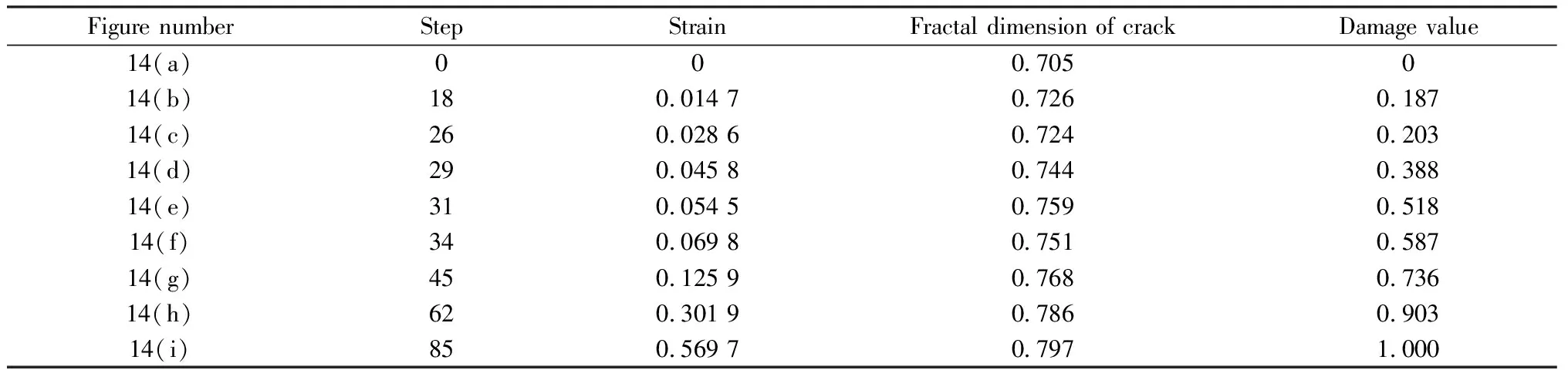
表4 损伤发展过程中各分析步对应的参数值Table 4 Parameter values corresponding to each analysis step in the damage development process

3.2.2 初始缝高比的影响

以0.5%体积掺量的钢纤维为基准，初始缝高比分别取0.3、0.4、0.5，研究初始缝高比对SFRC切口梁抗折强度和裂纹损伤演化的影响。根据上述分形维数和损伤值的计算方法，得到不同初始缝高比的SFRC切口梁各分析步对应的裂纹分形维数和基于裂纹分形维数的损伤值，将其绘制为3Y轴图，如图16所示。

由图16可知,初始缝高比为0.3和0.4的SFRC切口梁抗折强度分别为6.815 kN和4.801 kN，相较于初始缝高比为0.5的SFRC切口梁抗折强度3.273 kN分别提高了108.2%和46.7%，说明随着初始缝高比的增大，切口梁的整体刚度减小，导致切口梁的抗折强度明显降低。由裂纹分形维数曲线和损伤值曲线可知，不同初始缝高比的裂纹分形维数变化基本一致，但随着初始缝高比的增加，损伤值有所降低，这是缝高比的增加使得切口梁的整体刚度减小引起的。

图15 不同钢纤维体积掺量的SFRC切口梁损伤过程Fig.15 Damage process of SFRC notched beams with different steel fiber volume content

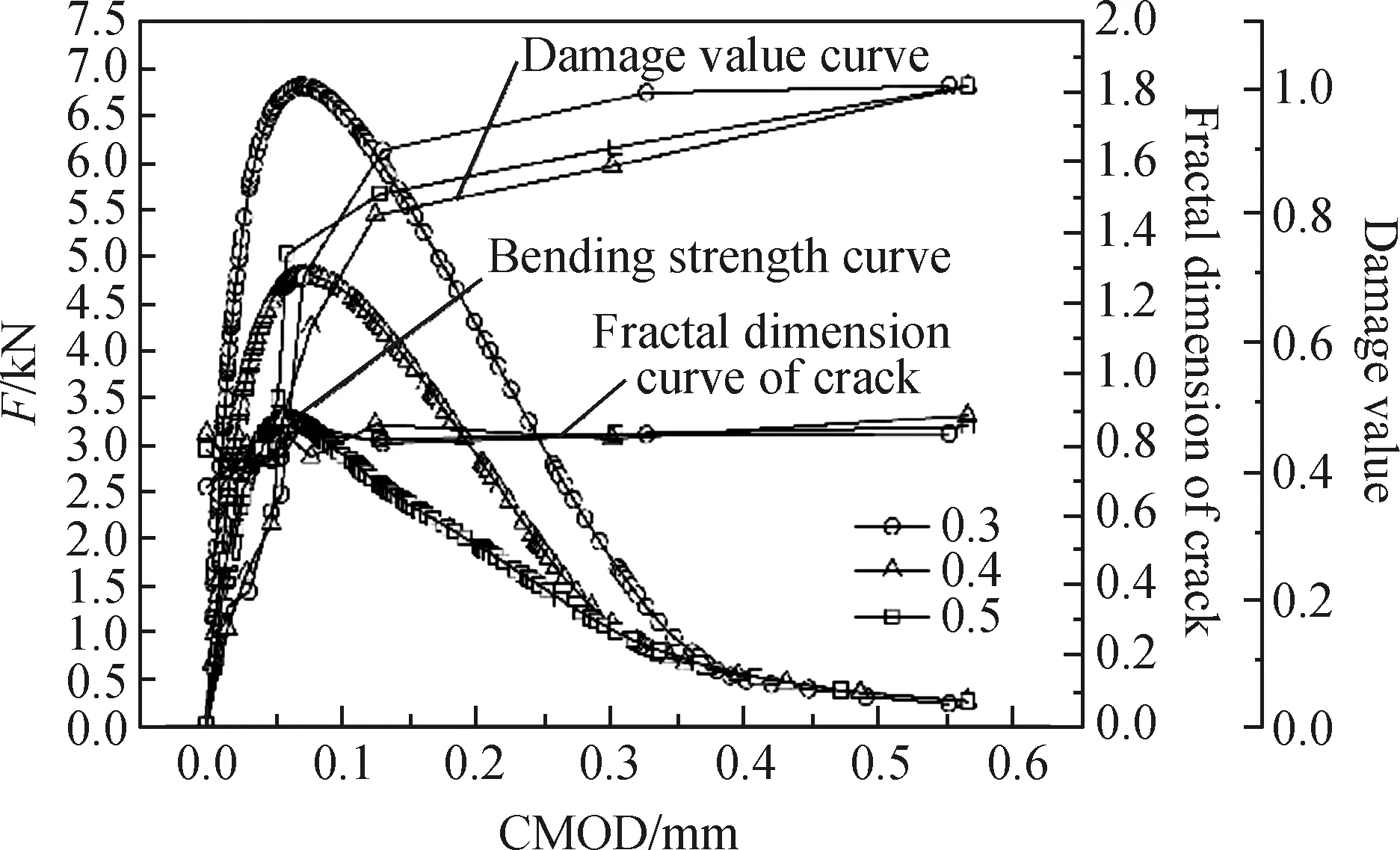
图16 不同初始缝高比的SFRC切口梁损伤过程Fig.16 Damage process of SFRC notched beams with different initial crack height ratios

图17 不同初始裂缝位置的SFRC切口梁损伤过程Fig.17 Damage process of SFRC notched beams with different initial crack positions

3.2.3 初始裂纹位置的影响

以0.5%体积掺量的钢纤维、0.4的初始缝高比为基准，研究初始裂纹位置对SFRC切口梁抗折强度和裂纹损伤演化的影响。根据上述分形维数和损伤值的计算方法，得到不同初始裂纹位置的SFRC切口梁各分析步对应的裂纹分形维数和基于裂纹分形维数的损伤值，将其绘制为3Y轴图，如图17所示。

由图17可知，初始裂纹距跨中50 mm和100 mm的SFRC切口梁抗折强度分别为5.376 kN和5.759 kN，相较于初始裂纹位于距跨中0 mm的SFRC切口梁的抗折强度4.801 kN分别提高了12.0%和20.0%。由裂纹分形维数曲线及抗折强度曲线知，随着预制裂纹距跨中距离的增加，裂纹分形维数趋于平稳的时刻相较于抗折强度峰值不断提前，裂纹的损伤演化过程有所减缓。这是由于距跨中的距离越远，所在位置承受的拉应力就越小，所以预制裂纹距跨中位置越远，SFRC损伤演化相对越慢。

4 结 论

(1)从各试件的损伤过程图可以看出，裂纹分形维数曲线和损伤值曲线具有较好的同步对应关系，且裂纹分形维数趋于平稳的时刻(裂纹扩展路径基本形成)基本都发生在应力曲线和抗折强度曲线的峰值及峰值前一段时间。此时刻之前，裂纹不断萌生，交汇，扩展，材料处于未劣化阶段，而在此时刻之后，裂纹扩展路径基本形成，材料损伤较大，材料开始表现出力学性能劣化等行为，说明基于裂纹分形维数的损伤值可以很好地反映SFRC的损伤变化过程。通过对数值计算结果进行统计分析表明：SFRC立方体试件抗拉试验达到应力峰值时，损伤值一般在0.870～0.944；SFRC切口梁三点弯曲试验抗折强度达到荷载峰值时，损伤值一般在0.587～0.737。

(2)钢纤维体积掺量、长度的增加使钢纤维和混凝土基体间的桥接作用增强，从而延缓了SFRC的损伤演化过程；椭圆形和不规则多边形骨料使SFRC中薄弱的骨料界面增加，使得裂纹扩展路径增多，裂纹发展过程所需的能量亦增大，从而延缓了SFRC的损伤演化过程。

(3)钢纤维体积掺量的增加、初始缝高比的减小和初始裂缝距跨中距离的增加都可以增加SFRC切口梁的抗折强度，并减缓其损伤演化过程。