基于双目视觉的掘锚机器人行驶位移检测方法

马宏伟，晁勇，薛旭升，毛清华，王川伟

（1.西安科技大学 机械工程学院，陕西 西安 710054；2.陕西省矿山机电装备智能检测与控制重点实验室，陕西 西安 710054）

0 引言

掘锚机器人是实现综掘工作面掘进与支护作业的集成装备，能够有效提高工人的工作效率。目前在巷道掘进过程中，主要依靠工人的施工经验调整掘锚机器人以完成掘进与钻锚作业，难以保证其定位精度和效率，容易造成工作面严重的超挖、欠挖与锚杆安装偏移等问题[1]。因此，为了实现巷道断面的高质量成型及精准支护，必须保证对掘锚机器人的行驶位移实现精准把控，以提升掘锚机器人系统的安全性、可靠性、自动化和智能化。

目前常用于井下掘锚机器人的定位方法主要有惯性导航系统、超声定位、全站仪定位、激光雷达定位及超宽带定位等[2]。惯性导航系统能够在短时间内精确检测位姿信息，但在长时间的运行过程中累计误差较大[3]；超声定位性价比高，但受距离、温度、光线等因素影响较大[4]；全站仪定位速度快，精度高，但需要人工搬运[5]；激光雷达体积小，分辨率高，但抗干扰能力差[6]；超宽带定位功耗低、抗干扰能力强，但通信距离短[7]。由于煤矿巷道环境复杂，各种机械设备繁多，使用传统定位方法具有局限性。双目视觉定位技术是一种基于双目视差原理计算像素点深度信息的技术，其采用非接触的视觉测量方式，能够有效利用巷道环境中已有特征，从中提取出必要的特征信息，以此解算机器人的位姿信息，能够有效降低定位系统的复杂度，极大地提升掘锚机器人定位系统的自主性[8]。双目视觉定位技术的核心是立体匹配算法，Census变换算法是目前使用最广泛的立体匹配算法[9]，但是采用传统Census变换算法得到的视差图具有局限性，为了增强传统Census变换算法的立体匹配性能，本文对Census变换算法进行了改进。文献[10]针对纹理弱和深度不连续区域误匹配的问题，在传统Census变换算法中引入像素差平均值的计算来自动调整匹配窗口的大小，该方法能够有效减少算法的运行时间并降低误匹配率，但对于遮挡区域的大面积视差失真现象仍不能有效地解决。文献[11]针对中心像素点突变问题，在传统Census变换算法中引入自适应中心像素值权重的视差估计，通过计算邻域像素点的平均值，以此来代替中心像素值，该方法减少了因中心像素点突变而发生的误匹配，但在色差变化过大的场景下，邻域像素平均值与中心像素值相差过大，仍然会造成较多误匹配。文献[12]在传统Census变换算法中引入自适应支持权值方法，在计算中心像素的同时，考虑欧氏距离与辐射差异的权重，能够有效保持图像边缘信息，但会将轮廓边缘的黑洞区域填满，呈现错误的物体轮廓。文献[13]在传统Census变换算法中引入多中心点融合监督方法，通过扩大匹配窗口，将1个中心像素点增加到4个像素点，通过相互融合监督的方式排除误匹配点，该方法能够大幅提升匹配率，但是增加了计算量，导致运行时间过长。

针对掘锚机器人行驶过程中存在位移检测精度低的问题，本文提出了一种基于双目视觉的掘锚机器人行驶位移检测方法。首先，针对煤矿井下复杂环境，对传统Census变换算法中的相似性检测函数进行改进，提高了双目立体匹配的精度；其次，利用图像处理算法识别并提取锚杆特征点，对特征点进行最小二乘法空间直线拟合，在此直线上建立平行于截面的平面；最后建立“掘锚机器人−已支护锚杆”定位模型，进行模拟定位实验并分析定位误差。

1 掘锚机器人视觉测距方法原理

通过在掘锚机器人机身顶部安装双目相机，监测机器人后方巷道顶部的已支护锚杆，分析掘锚机器人、双目相机与已支护锚杆的空间位置关系，建立基于分布式锚杆的双目视觉测距模型，并通过模型计算得出双目相机位置信息，求解掘锚机器人在巷道中相对于锚杆的行驶距离。

视觉定位原理如图1所示。以双目相机光心为坐标原点，以沿掘锚机器人垂直于侧帮方向、竖直方向和前进方向分别为x轴、y轴和z轴，建立三维坐标系，设D为双目相机与锚杆特征点之间的空间距离，E为双目相机与锚杆所在平行于截面的平面（简称平行截面）之间的垂直距离，通过几何关系解算E，即可得到掘锚机器人相对于已支护锚杆的行驶距离。

图1 视觉定位原理Fig.1 Visual positioning principle

视觉测距系统主要由视觉信息获取模块、误差分析模块和机身运动控制模块组成，如图2所示。视觉信息获取模块对图像进行预处理，提取图像中所需的特征信息，并将其转换为视觉信息。误差分析模块对视觉信息进行分析，将计算得到的位移距离与理论位移距离进行对比，得到机身行驶位移误差。将运动距离误差传入机身运动控制模块，由机身运动控制卡发送误差补偿数据，同时向行驶机构下发控制指令以驱动机身行驶到预计的位置。

图2 视觉测距系统结构Fig.2 Structure of vision ranging system

视觉信息获取模块是视觉测距系统的核心部分，主要步骤如下：

（1）相机标定与立体校正。通过双目相机采集锚杆的原始图像，再通过相机标定后得到相机的畸变系数、内外参矩阵等参数，对采集到的图像进行立体校正。

（2）双目立体匹配。对校正后的左右视图采用Census变换算法进行匹配代价计算，得到视差图，由此可得到图像中像素点的深度信息。

（3）锚杆轮廓特征提取。采用Sobel边缘检测算法对视差图中的锚杆进行轮廓特征提取，突出锚杆轮廓特征。

（4）锚杆特征点提取。根据锚杆轮廓特征，采用最小外接矩形与最大外接矩形组合算法（简称组合外接矩形算法）提取锚杆轮廓的边界点，选取锚杆与顶板相接处的边界点为特征点，输出其像素坐标。

（5）特征点坐标转换。通过分析锚杆特征点像素坐标与掘锚机器人世界坐标的转换关系，将锚杆特征点像素坐标转换为世界坐标。

（6）特征点空间直线拟合。采用最小二乘法将同一排锚杆的特征点世界坐标拟合成一条直线，在该直线上建立平行截面，计算相机与平行截面的距离。

2 双目立体匹配视差图获取

2.1 分布式锚杆多目标双目视差原理

双目视觉测距原理如图3所示。其中，P为锚杆特征点，Ol，Or分别为左右相机光心，Pl，Pr分别为P点在左右相机成像平面上的成像点，OCl-XYlZl，OCr-XYrZr分别为左右相机的图像坐标系。左右相机光心发射2条射线，在同名点处相交，以此确定唯一目标点，通过三角法计算出目标点与相机之间的距离信息[14]。

图3 双目视觉测距原理Fig.3 Binocular vision ranging principle

根据掘锚机器人作业需求及锚杆分布特点，建立基于分布式锚杆的双目视觉定位模型，如图4所示。其中Pi（i=0，1，···，n，n为特征点总数）为第i个锚杆特征点，f为相机焦距，B为光心之间的距离（基线），Z为被测特征点与相机光心之间的距离，xl，xr分别为特征点在左右相机像素坐标系上的x轴坐标值，两值相减即为该特征点的视差值d。

图4 双目视觉定位模型Fig.4 Binocular vision positioning model

根据相似三角原理有

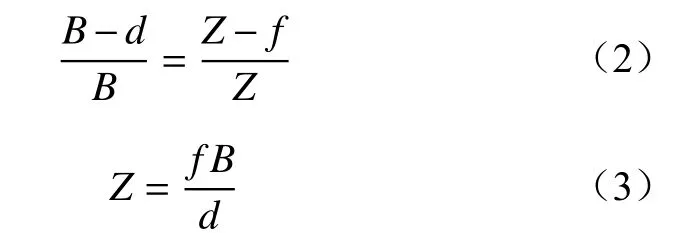
2.2 传统Census变换算法原理

传统Census变换算法是在一幅图像中以某个像素为中心创建一个3×3矩形窗口，将窗口内邻域与中心像素的灰度值进行比较，若邻域像素灰度值比中心像素灰度值小，则比特串相应位置的值记为1，反之记为0[15]。

式中：为结果判定函数；p，q分别为窗口中心像素灰度值和其他邻域像素灰度值。

将判定结果串联，得到Census变换算法的比特串CT。

式中：W为中心像素灰度值p的邻域；为按位连接符。

窗口中所有像素点经过Census变换算法后，得到相应的比特串，通过汉明距离对2个比特串值进行异或运算，以此作为匹配代价的值。

式中：A（s,d）为2个比特串对应位数值不同的数量，即匹配代价值；s为左图像素点；H为汉明距离计算函数；CTl（s）为左图像素点的比特串；CTr（s，d）为右图中对应像素点的比特串。

传统Census变换算法的核心思想是由匹配代价值A（s,d）来判定2个像素点的相似性，A（s,d）的值越小，则2个像素点的相似度越高。

2.3 改进Census变换算法

煤矿井下环境中存在大量重复纹理与深度不连续区域，采用传统Census变换算法的误匹配率高。因此，本文在传统Census变换算法的基础上加入绝对值比较参数，对传统Census变换算法进行改进，使原算法获得更好的匹配窗口判断性，提高匹配精度与视差图效果，以适应煤矿井下的复杂环境。

将2个待匹配窗口的中心像素点p与其他邻域像素点q的像素值相减并将结果进行串联，再将2组串联结果按位做差并取绝对值。

式中：LT（p）为左图窗口经过变换得到的比特串；RT（p）为右图窗口经过变换得到的比特串；WT为2组比特串按位做差并取绝对值得到的新比特串。

再取2组WT中的元素按位进行比较，其值大的元素在相应位上记为1，反之记为0。

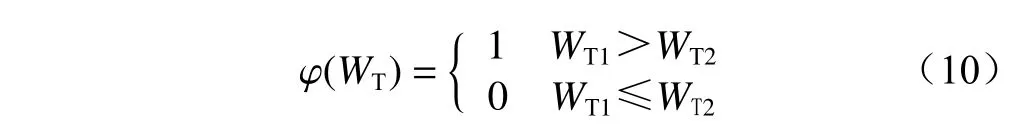
式中φ（WT）为WT的相似度比较函数。

将相似度比较函数φ（WT）得到的比较结果相加，其值越小则2个窗口的相似度越大，其值越大则2个窗口的相似度越小，取值最小的窗口作为正确的匹配窗口。

传统Census变换算法和改进Census变换算法对3个高相似度窗口的匹配结果如图5所示。可看出传统算法中，左图窗口与2个右图窗口内的像素信息都存在不同程度的差异，经过传统Census变换算法得到的比特串一致，由汉明距离计算得到相同的匹配代价值，表明左图窗口与2个右图窗口有着相同的相似度，而实际上，左图窗口与右图窗口2的相似度更高，故在匹配过程中容易发生误匹配现象；经过改进Census变换算法对2组窗口进行相似度计算并选择最小值，成功匹配到了相似度更高的窗口。由此可知，改进Census变换算法具有更强的相似度判断性，可以更精确地反映2组窗口的相似程度。

图5 Census变换算法改进前后对比Fig.5 Comparison of Censustransform algorithm before and after improvement

3 锚杆特征点识别与定位

3.1 锚杆特征点识别

为了保证锚杆特征点处在一条水平线上，选取锚杆与巷道顶板的相接点作为特征点，对其进行识别与提取。采用图像处理技术在改进Census变换算法得到的视差图中分割并提取出感兴趣区域（ROI）[16]，将ROI作为输入图像进行处理，如图6所示。首先将获取的锚杆视差图转为灰度图像，对其进行高斯去噪处理，并采用Sobel算子计算图像梯度，得到图像边缘幅值与角度。然后沿梯度方向进行非极大值抑制，对锚杆轮廓进行边缘细化，经过双阈值边缘连接处理，消除细小的尖刺，修复断开的连接并去除局部小面积的干扰特征，输出较为完整的锚杆轮廓的二值化图像。最后对二值化图像采用组合外接矩形算法提取锚杆特征点，选取最顶部的点作为特征点，并输出其像素坐标，实现锚杆特征点提取的目标。

图6 图像处理流程Fig.6 Image processing flow

3.2 像素坐标到世界坐标系的转换

经过图像处理后得到锚杆特征点的像素坐标值，采用坐标转换原理将像素坐标值转换为世界坐标值，转换关系如图7所示。其中，OW-XWYWZW为世界坐标系，OC-XCYCZC为相机坐标系，oxy为图像坐标系，uv为像素坐标系，像素坐标系是以像素为单位，其余坐标系均以毫米为单位。Q点为世界坐标系中的任意一点，其在世界坐标系下的坐标为Q（xW，yW，zW），在相机坐标系下的坐标为Q（xC，yC，zC），G点为Q点在图像中的成像点，在图像坐标系中的坐标为（x，y），在像素坐标系中的坐标为（u0，v0）。

图7 坐标系转换关系Fig.7 Coordinate system conversion relationship

从世界坐标系到相机坐标系的转换涉及到旋转和平移，绕着不同的坐标轴旋转不同的角度，得到相应的矩阵。Q点在相机坐标系中的坐标为

式中：S为机身坐标系与世界坐标系间的旋转矩阵；T为相机坐标系与世界坐标系间的平移向量。

结合双目视差原理和坐标系转换关系，即可求得图像中像素点对应的世界坐标值。从相机坐标系到图像坐标系的转换属于透视投影关系，由相似三角形原理可得

图像坐标系到像素坐标系的转换关系为

像素坐标系到世界坐标系的转换关系为

3.3 锚杆特征点直线拟合

根据掘锚机器人定位原理，需将同一排锚杆特征点拟合成平行于截面的直线。由于受到锚杆安装误差及计算误差影响，在同一排锚杆中，各个特征点与相机间的距离各不相同，故采用最小二乘法对同一排锚杆特征点进行空间直线拟合[17]。因为特征点空间坐标的y值只影响拟合直线的上下位置，与前后位置无关，故在直线拟合时只需考虑x值与z值。

式中：Kε为真实值与预测值误差；（xi，zi）为已知坐标点；z为zi的拟合值；a为直线斜率；b为y轴截距。

因为要求拟合出的空间直线在平行截面中，故该直线必须平行于x轴，即令a=0，可得

由此可根据坐标点得到拟合直线所在平面xoz上的垂直投影。

式中l为相机与平行截面之间的垂直距离。

经过直线方程构建平行截面，建立“掘锚机器人−已支护锚杆”定位模型，如图8所示。其中α，β，χ分别为锚杆特征点拟合直线所建立的平行截面，l1，l2，l3分别为相机光心与平行截面之间的垂直距离。将li作为相机与平行截面之间的距离信息，来计算掘锚机器人的行驶位移。

图8 “掘锚机器人−已支护锚杆”定位模型Fig.8 Positioning model of “anchor digging robot-supported bolt”

4 机器人视觉定位实验验证

为了验证掘锚机器人定位方法的可行性，搭建移动机器人平台进行行驶位移检测实验。位移检测系统由双目相机、锚杆、计算机及履带式移动机器人组成，其实验平台如图9所示。将锚杆并排放置在地面上，代替安装在巷道顶部的锚杆；将双目相机置于距离锚杆1 m处进行拍摄，在实验过程中，保持相机水平向前移动，以模拟掘锚机器人在巷道中的行驶状态。

图9 位移检测系统实验平台Fig.9 Experiment platform of displacement detection system

以掘锚机器人为研究对象，相机光心为坐标系原点，建立世界坐标系。其中以垂直于侧帮方向为x轴，垂直于顶板方向为y轴，掘锚机器人前进方向为z轴。实验场地如图10所示，设锚杆排距I=800 mm，每排锚杆的分布距离M=2 000 mm，相机距第3排锚杆的距离N=1 400 mm。由于双目相机的有效测距范围为4 000 mm，故仅取距相机最近的前3排锚杆进行测量。通过对测量值与理论模型计算值进行误差分析，从而实现实验平台的视觉测距、移动控制和轨迹跟踪。

图10 实验场地Fig.10 Sketch map of experimental filed

4.1 Census变换算法改进效果

为了获取准确的锚杆图像，在定位系统实验平台采用Matlab双目相机工具箱进行相机标定与立体校正，校正前后结果如图11所示。

图11 校正前后结果Fig.11 Resultsbefore and after correction

使用双目相机采集一排锚杆图像，提取其ROI图形，分别采用改进前后Census变换算法对ROI图形进行视差图处理，如图12所示。可看出改进后Census变换算法改善了锚杆边缘的失真区域，得到了较明显的锚杆轮廓特征及更准确的深度信息。

图12 改进前后视差图效果对比Fig.12 Effect comparison of disparity before and after improvement

算法性能对比结果见表1。可看出改进Census变换算法的匹配精度显著提升，比传统Census变换算法误匹配率降低了41.96%，但是由于计算过程较为复杂，导致运行时间也有一定的增加。

表1 算法性能对比Table 1 Comparison of algorithm performance

为验证不同视差初始值对算法性能的影响，取初始视差值为[−13，7]对算法性能进行验证，对比结果如图13所示。可看出当视差范围缩小时，误匹配率及运行时间均有所降低。因此，在保留完整锚杆图像的情况下，可设定较大的视差初始值，以降低误匹配率并减少运行时间。

图13 不同视差初始值下的性能对比Fig.13 Performancecomparison under different parallax initial values

4.2 锚杆特征点识别与定位

（1）锚杆特征点提取与坐标转换。对校正后的锚杆图像进行特征点坐标提取，由于锚杆放置在地面上，故以锚杆底部的端点为特征点，对其进行提取。首先采用改进后的Census变换算法对相机原图进行处理，得到锚杆图像的视差图，然后对视差图进行Sobel算子轮廓检测提取锚杆轮廓，最后采用组合外接矩形算法对锚杆轮廓进行处理并将锚杆特征点用蓝色圆点标记出来，锚杆特征点提取结果如图14所示。

图14 特征点提取结果Fig.14 Extraction results of anchor feature points

将提取出的特征点像素坐标转换为世界坐标，坐标转换结果见表2。

表2 特征点坐标转换结果Table 2 Coordinate conversion resultsof featurepoints

（2）特征点直线拟合。由于同一排锚杆特征点位置在z轴上存在偏差，所以无法确定相机与这排锚杆之间的距离，因此，根据特征点直线拟合原理，将特征点拟合成平行于x轴的直线，拟合结果如图15所示。可看出经过直线拟合后，消除了不同特征点间的位置误差，得到了与特征点位置紧密关联的直线。

图15 特征点拟合直线结果Fig.15 Straight line fitting results of feature points

（3）特征点平行截面建立。经过特征点拟合直线建立平行截面，如图16所示。可看出相机与3个平行截面之间的距离分别为3 010.428，2 215.910，1 415.127 mm。

图16 特征点平行截面Fig.16 Parallel section of feature points

在机器人移动过程中，通过计算得到相机与平行截面之间的距离，根据锚杆在模拟巷道中的安装位置，即可得到移动机器人在世界坐标系下的行驶位移。

4.3 移动机器人定位实验

在实验场地上放置10排锚杆，排距为800 mm，移动机器人起始位置在距第1排锚杆800 mm处，控制移动机器人沿着z轴方向前进8 000 mm，前进速度为0.25 m/s，双目相机采集锚杆图像频率为5 Hz。以第1排锚杆为定位基准，控制机器人沿z轴前进，依次拍摄锚杆图像，计算相机与锚杆平行截面的距离，以此求解机器人行驶的位移。

在进行机器人定位实验时，将计算位移与理论位移进行对比，如图17所示。可看出移动机器人在整个定位实验过程中，理论位移曲线与计算位移曲线基本重合。

图17 运动轨迹对比曲线Fig.17 Comparison curve of motion track

通过对比相机的理论位移与计算位移得到两者的误差分布，如图18所示。可看出理论位移与计算位移误差不超过20 mm，能够保证掘锚机器人的定位精度，可实现掘锚机器人的自主、准确、实时位移检测。

图18 运动轨迹误差分布Fig.18 Error distribution of motion track

5 结论

针对掘锚机器人行驶过程中存在位移检测精度低的问题，提出了一种基于双目视觉的掘锚机器人行驶位移检测方法。该方法以已支护锚杆为定位基准，利用双目视觉检测掘锚机器人的行驶位移，解决了掘锚机器人在井下行驶无参考目标的问题，提高了双目视觉在煤矿井下环境中的适应性与定位精度，实现了掘锚机器人行驶位移的精确检测，为掘锚机器人的定位提供了有效解决方案。

（1）改进后的Census变换算法修复了锚杆图像的失真区域，能够得到效果较好的视差图，并使误匹配率从19.85%降低到11.52%，较传统Census变换算法的误匹配率降低了41.96%。

（2）当视差范围缩小时，误匹配率及运行时间均有所降低。因此，在保留完整锚杆图像的情况下，可设定较大的视差初始值，以降低误匹配率并减少运行时间。

（3）经过直线拟合后，消除了不同特征点间的位置误差，得到了与特征点位置紧密关联的直线。在拟合直线上建立平行截面，得到相机与3个平行截面的距离分别为3 010.428，2 215.910，1 415.127 mm。

（4）由模拟实验可知，理论位移曲线与计算位移曲线基本重合，理论位移与计算位移误差不超过20 mm。说明基于双目视觉的掘锚机器人行驶位移检测方法能够保证掘锚机器人的定位精度，可实现掘锚机器人的自主、准确、实时位移检测。