面向同步辐射光源图像的可并行智能压缩方法

符世园，张敏行，高宇，汪璐，程耀东，3

（1.中国科学院高能物理研究所，北京 100049；2.中国科学院大学，北京 100049；3.中国科学院高能物理研究所天府宇宙线研究中心，成都 610041）

0 概述

高能同步辐射光源（High-Energy Photon Source，HEPS）是我国重大科技基础设施。一期建设的实验线站预计每天会产生数百太字节的原始实验数据［1］，海量数据对存储和传输带来极大压力。数据压缩作为一种减少数据量的方法可以用于缓解该问题。实验线站产生的数据中占比最高的是硬X 射线实验线站产生的图像数据。硬X 射线实验线站利用硬X 射线的穿透能力扫描样本，产生16 位单通道灰度图。在相邻成像间隔中，样本均围绕自身中心轴旋转一个极小的角度，每扫描一个样本会产生成百上千张二维投影图像。

压缩方法按照信息有无损失可以分为有损压缩和无损压缩。在有损压缩中，不相关或者不重要的数据被直接忽略，解压后得到的数据与原始数据不同。在无损压缩中，每个细节都会被保存，只有统计冗余被消除，可完整重构原始数据。由于该成像线站采集图像的目的是用于探索物质内部结构，因此为保证数据的科学潜力，采用无损压缩保证图像信息的完整性。但是，通用图像无损压缩方法对光源图像压缩效果不佳。

近年来，人工智能技术得到了飞速发展。在数据无损压缩领域，深度学习技术也受到了越来越多的关注，已有研究人员将Softmax 层作为压缩的一部分与传统编码方法相结合，用于探索文本压缩比的优化。本文提出一种面向同步辐射光源图像的可并行无损压缩方法，充分利用光源图像的相关性，以参数自适应的可逆量化方法和非线性预测方法实现对光源图像的智能化压缩，逐步降低存储光源图像所需要的资源。针对算术编码效率问题，设计概率距离量化方法提升编码并行度，最终达到提高图像压缩比的同时完全保留数据科学潜力并且使其具有高并行度。

1 相关工作

1.1 通用无损压缩方法

无损图像压缩方法可以分为熵编码、预测编码、变换编码和基 于字典的编码［2］4 类。Huffman 编码［3］、算术编码［4］等熵编码在编码过程中，首先通过概率估计生成编码表，概率可通过全局统计生成，也可由局部信息生成，然后通过编码表消除编码冗余。预测编码通过图像空间结构进行像素值预测，再将预测值与真实值之间的残差通过熵编码压缩，从而达到无损压缩的目的，例如：WebP［5］基于3 个相邻块预测当前块；PNG［6］可通过可选的5 种类型的过滤器进行预测，不同类型的过滤器对周围的像素值进行不同的计算得到预测值；FLIF［7］通过上下文模型结合熵编码进行压缩；JPEG_LS［8］中当前像素的预测值取决于局部边缘方向的自适应模型。变换编码是将空域转变到频域进行无损压缩，例如JPEG2000［9］使用可逆的小波变换。基于字典的编码是通过字符串表进行压缩，例如LZW 将像素分组为字符串，最后转换成编码。

视频冗余除了图像中存在的空间冗余和编码冗余外，还包括时间冗余，所以视频无损压缩方法可以进一步从时间维度上进行预测。FFV1［10］是一个简单高效的无损帧内编码器，可使用可变长度编码或算术编码进行熵编码。因此，通用压缩方法主要包括变换、量化、预测、编码4 个步骤，而由于这些步骤中量化过程不可逆，无损压缩直接跳过该步骤。此外，通用图像无损压缩方法可以有效地利用图像的局部结构，而通用视频无损压缩方法可以进一步消除图像序列内部的时间冗余，但是只能捕获手工指定的简单统计信息。为解决这两个问题，本文结合同步辐射光源图像的特点，提出一种完全可逆的分区量化方法，通过基于深度学习的无损压缩方法提升压缩效果。

1.2 基于深度学习的无损压缩方法

近年来，深度学习技术在诸多任务中取得了达到或超越传统通用方法的性能。由于数据量的持续爆发性增长，越来越多的研究人员将深度学习技术应用于无损压缩。在无损压缩任务中最关键的是准确的概率估计，深度学习方法主要用于预测阶段，利用训练得到的概率模型对数据分布进行建模，与熵编码结合对残差进行无损编码，最大化模型在真实值上的预测概率，等同于最小化使用编码器的无损压缩模型所获得的比特率［11］。

在图像无损压缩任务中：文献［11］通过建模低分辨率与高分辨率图像的还原过程，从低分辨率图像直接得到预测图像的概率分布，结合算术编码进行压缩；文献［12］结合通用的有损图像压缩方法构建无损图像压缩，利用CNN 对残差分布进行建模；文献［13］通过基于流的方法将输入图像转换为具有预定义分布函数的潜在表示，编码和解码函数必须互为可逆，并使用大型神经网络提高压缩性能。在科学数据的压缩任务中，深度学习方法也得到广泛的应用：文献［14］提出一种基于神经网络的DNA 序列压缩器，在压缩效果上得到一定的提升；文献［15］使用深度递归神经网络来改进传统方法并提高模型的泛化能力和预测精度。

上述基于深度学习的压缩方法建模追求泛化性和通用性。与上述压缩方法不同，GOYAL 等［16］在DeepZip 中提出一种基于时序网络的文本无损压缩方法，该方法针对不同的数据过拟合训练独立的模型，为保证压缩过程完全可逆，将模型与压缩结果一并保存，即压缩数据与模型为一对一关系，模型仅适用于训练数据的压缩任务。这种对不同数据过拟合建模的方式可在其测试数据上优化压缩比，但是模型规模会带来额外的存储空间开销。对于模型规模影响压缩效果的问题，文献［17］提出一种基于自适应和半自适应训练的新型混合架构，无需重新训练模型即可压缩新的数据。同时，基于深度学习的无损压缩方法通常编码速度较慢，低编码速率限制了应用的可行性。针对这一问题，文献［18］提出一种多尺度的渐进统计模型加速模型推理速度，文献［19］通过流模型进行加速，文献［20］通过并行预测多个像素的概率进行加速，文献［21］通过跳过耗时较长的编码阶段进行加速。

本文通过提出概率距离以及稳定的计算过程替换算术编码过程，在保证压缩比优化的前提下提高编码过程的并行度。受DeepZip 启发，结合光源图像特点，以数据集为单位过拟合训练模型，减少模型规模对压缩比提升的影响。

2 图像数据集建立与相关性分析

2.1 图像数据集建立

本文图像数据来自上海同步辐射光源装置，是扫描不同样本得到的图像序列，涵盖了鱼鳞、菌丝、小鼠脑和化石翅膀。不同图像序列的帧数和图像尺寸有所不同，分辨率为2 048×2 048 像素和2 048×1 200 像素两种，均为16 位单通道灰度投影图序列，具体信息如表1 所示。

表1 数据集信息Table 1 Dataset information

分别对上述图像序列使用通用无损压缩方法进行压缩测试，得到结果如表2 所示，压缩结果以压缩比（Compression Ratio，CR）衡量，压缩比即为压缩前文件大小与压缩后文件大小的比值。通用无损压缩方法达到的最优压缩比为1.46～1.64。压缩比越高，说明节省的存储空间越多，数据长期存储的成本越低。

表2 4 种通用压缩方法的压缩比Table 2 CR of four general compression methods

2.2 图像线性相关性分析

对于图像相似度的衡量指标，Spearman 系数［22］比SSIM［23-24］更准确，因此以Spearman 系数为图像间线性关系的衡量标准。同一样本图像序列内部的时间线性相关性由相邻图像间线性相关性的均值计算得到。

图像序列内部的部分时间线性相关性通过时间差分去除。时间差分即将相邻帧同一空间位置像素相减，该过程也可以看作将前帧作为后帧的线性预测帧，差分后得到去除部分线性冗余后的残差数据，残差数据可通过深度学习方法建模非线性关系进一步压缩。

差分前后图像序列内部的线性时间相关性如表3 所示，差分前图像序列内部具有极强的线性时间相关性，差分后其相关性接近于0。因此，差分可以简单有效地去除图像序列内部的时间线性相关性。

表3 图像差分前后的相关性对比Table 3 Comparison of correlation before and after image difference

3 同步辐射光源图像智能压缩

3.1 整体流程

本文提出一种面向同步辐射光源图像的可并行智能无损压缩方法，如图1 所示，主要包括线性预测和非线性预测，用以分别去除图像序列中的线性及非线性冗余信息。以时间差分作为去除线性冗余的线性预测方法，差分后的图像通过分区量化方法将像素值取值范围映射到一个更小的区间，以减小像素值所占比特位，得到images′。在非线性预测模块中，通过预测模型及训练方法以加速训练及预测过程，定义概率距离概念以加速编码过程，将概率距离量化流作为最终压缩流。

图1 整体压缩流程Fig.1 Overall compression process

3.2 分区量化

由于光源图像序列内部时间线性相关性较强，因此通过时间差分方法去除序列内部的大部分时间线性冗余。时间差分前图像像素值分布如图2（a）所示，时间差分后图像像素值集中分布在0 和65 535 附近，该范围中部仅有少量数据存在，如图2（b）所示。将像素值映射到较小的数据范围能够缩小其所占比特位，从而达到压缩的目的，因此本文提出可逆的分区量化方法，以保存少量未压缩数据为代价，换取较小的数据分布范围。

图2 菌丝图像差分前后的像素值分布对比Fig.2 Comparison of pixel value distribution before and after difference

该量化过程完全可逆，因此可以保证反量化后数据与量化前数据一致。分区量化与反量化过程如图3 所示，在分区量化后，原始数据分为待压缩数据和直接保留数据，其中直接保留数据直接按顺序单独存储。为保证无损还原，直接保留数据以占位符的形式存在于待压缩数据中。在反量化时，在待压缩数据中扫描到占位符时，按顺序回填直接保留数据即可。待压缩数据量化方法为向右平移指定距离，在还原时需向左平移相同距离。

图3 分区量化与反量化过程Fig.3 Process of partition quantization and inverse quantization

对于T×M×N的图像序列，其中，T为帧数，M为高度，N为宽度，分区量化步骤具体如下：

1）采样：从图像序列中等间隔抽取一定数量样本。

2）统计像素值：统计采样数据集中像素值的分布得到Dict，记录每一个像素值出现的次数，Dict（i）表示值为i的像素值出现的次数。

3）确定占位符f：由占位符确定数据的量化函数，依据式（1）确定占位符：

4）构造量化函数F（x）：x为分区量化前的差分像素值，根据占位符构造量化函数，约定占位符为量化后范围末尾加1 的值。待压缩数据后，只需向右平移指定步长（f-1）/2，直接保留数据并映射到占位符，按顺序存储到文件中，如式（2）所示：

5）量化：根据量化函数将数据量化到新的值。

分区反量化步骤具体如下：

1）确定占位符f：由于占位符的设置是新的映射范围最大值加1，因此待压缩数据的最大值即为占位符的值。

2）构造反量化函数G（y）：该过程为量化函数逆过程，y为量化后的值。若数据等于占位符，则从直接保留数据中读取一个数据，否则向左平移指定步长（f-1）/2，如式（3）所示：

3）反量化：根据反量化函数还原量化值。

在分区量化过程中，主要包括像素值统计、占位符确定、量化（反量化）过程，这3 个过程均可并行计算。

3.3 非线性预测

图像序列经过差分及量化后，已去除部分线性冗余并将像素值映射到较小范围。非线性预测用于利用差分量化后图像序列的非线性相关性进一步提升压缩比。受DeepZip 启发，使用深度学习方法过拟合压缩数据，学习其非线性相关性。但是该方法存在以下问题：1）由于模型规模较大，因此抵消了压缩所节省的空间；2）一对一训练过程耗时；3）模型预测时间较长。对于问题1 和2，结合同步辐射光源图像的特点，提出一种以数据集为单位，用少量数据训练模型以压缩整体数据的方法；对于问题3，提出一种以CNN 为基础架构的概率预测模型，以提高预测的并行度。

3.3.1 训练与预测方法

本文将压缩方法分为通用压缩与专用压缩两类，如图4、图5 所示。通用方法是由专门的组织提出标准编写而成的，对大部分图像数据具有压缩效果。专用方法如DeepZip，压缩器仅对训练数据有效。

图4 通用压缩中数据与压缩器的对应关系Fig.4 Correspondence between data and compressors in the general compression

图5 专用压缩中数据与压缩器的对应关系Fig.5 Correspondence between data and compressors in the special compression

基于同步辐射光源图像中一个样本对应一个数据集的特点，本文提出一种压缩粒度介于通用与专用之间的非线性预测方法，如图6 所示，每一个数据集即为一个图像序列。该方法以专用压缩的思想提升压缩比，即对不同的图像序列训练不同的模型，这是因为不同样本生成的图像序列内容差别较大。由于同一样本生成的图像序列内容非常相似，因此借鉴通用压缩的思想加速训练过程，即对同一图像序列使用统一的模型进行预测。在本文的训练与预测方法中，以数据集为单位过拟合训练独立模型，训练数据为样本图像序列中的单张图像及其前序图像组成的小样本数据集，用于该样本所有图像的压缩。

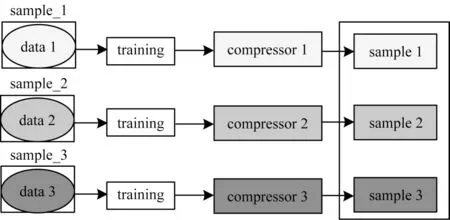
图6 本文中数据与压缩器的对应关系Fig.6 Correspondence between data and compressors in this study

3.3.2 C-Zip 网络结构

概率预测模型C-Zip 以CNN 为基础架构，输入为指定patch 大小，如图7 所示。该模型主要基于TCN［25］和Octave Convolution［26］。

图7 C-Zip 网络结构Fig.7 C-Zip network structure

TCN 是一种通过因果卷积和膨胀卷积学习序列的非线性关系的模型，仅使用CNN 模型，可大规模并行处理。本文方法利用3D-TCN 学习图像序列中的时空特征，最后通过Fully-Connected 层加Softmax层得到编码时使用的预测概率分布，其中3D-TOCN子模块如图8 所示。该子模块结合了Octave Convolution，将输入按通道切分为高频和低频，低频数据所含信息量较少，可以在高度和宽度的维度上缩小为原来的1/2，之后分别通过3D-TCN 学习频域内非线性关系，通过Octave Convolution 进行频域间通信，最后将低频信息通过上采样恢复成原始大小，与高频信息做拼接即得到最后的输出。

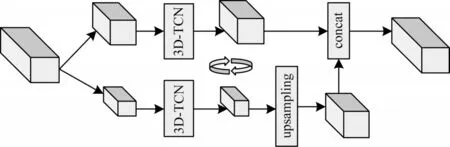
图8 3D-TOCN 子模块结构Fig.8 3D-TOCN submodule structure

3.4 概率距离

由于算术编码速度慢，并行度低，影响压缩效率，因此本文提出概率距离方法（Rank）用以增加编码并行度。

Softmax 层的输出根据不同的任务可以得到不同的解读与计算，从而提取出不同的信息。Softmax的输出经过归一化后可以认为是每个值对应的概率。对于压缩问题，概率可直接与熵编码进行结合；对于多分类问题，预测类别为最大概率值对应的类别；对于推荐问题，需对概率进行排序。本文针对的问题是大字典数数据压缩，对于大字典数据而言，若神经网络预测的结果较好，则大部分真实值对应的概率距离在Top-K中，当K的比特位数小于当前数据的比特位数时，可结合分区量化达到压缩效果，因此可通过概率距离结合分区量化达到压缩的目的。

概率距离方法定义为真实值对应的预测概率值在预测概率向量中的排序位置，针对概率值相同导致排序不稳定的问题，进一步比较字典中值的大小，保证计算过程完全可逆。

对于字典数为［0，n-1］的数据，当前待编码数据为v，模型输出为预测概率向量p，p［j］为字典数j对应的概率值，其中0≤j≤n-1，概率距离计算如式（4）及式（5）所示：

目前，在传统智能压缩方法中，将模型的输出看作概率，结合算术编码进行压缩。本文根据神经网络输出计算得到概率距离，结合分区量化进行压缩，如图9 所示。该方法计算简单，因为仅涉及比较大小和做统计的过程，而不同像素值概率距离的计算相互独立，所以并行度高。同时，该方法的输出可以继续与其他编码方法相结合，进一步提升压缩比。

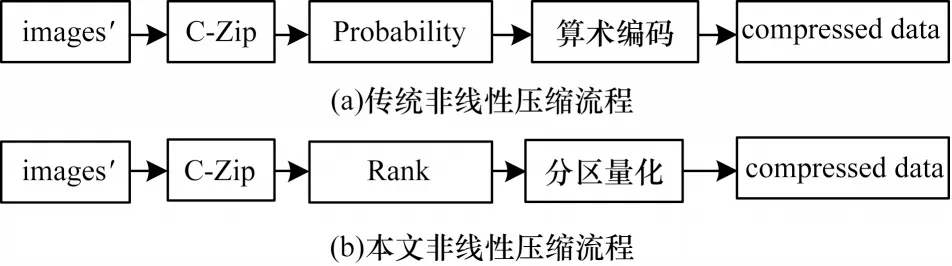
图9 非线性压缩流程Fig.9 Process of nonlinear compression

4 实验与结果分析

4.1 分区量化分析

对不同数据集进行时间差分，图10 和图11 为不同数据集中单张图像差分前后的像素值分布对比，其中，差分前不同数据集图像像素值分布的范围和密度不同，差分后不同数据集图像像素值的分布范围均密集分布在两端区域。因此，不同数据集时间差分后均可通过分区量化缩小像素值分布范围。

图10 原图像素值分布Fig.10 Pixel value distribution of original images

图11 差分图像素值分布Fig.11 Pixel value distribution of difference images

对每个数据集的图像序列抽取1/100 的数据统计其像素值并计算其占位符，结果如表4 所示。不同样本的占位符有所不同，说明分区量化的计算具有数据自适应性。量化后像素值所占比特位由16 位降低至11 或12 位，而保留数据只占原始数据的0.29%～1.97%，说明量化后数据可以达到压缩的目的。

表4 不同数据集上的分区量化结果Table 4 Partition quantization results on different datasets

因此，分区量化可以达到将数据无损量化到较小数据范围的目的，能够节省20%以上的存储空间，同时较小的数据分布范围有利于后续基于深度学习的模型训练与压缩。

4.2 非线性预测方法对比

数据集图像序列进行时间差分及分区量化后，通过非线性预测方法进行概率预测，直接结合算术编码进行压缩。

模型的输入维度为3×32×32，即将图像数据分块处理，块大小为32×32 像素，利用当前帧的前向3 帧不同图像块预测当前帧相应图像块每一个像素值的概率分布，损失函数为交叉熵损失函数，损失连续3 个epoch 不下降或者epoch 达到16 时停止训练，学习率设置为0.01，使用Adam 优化器，每3 个epoch学习率下降10%，Octave Convolution 中超参数设置为0.5。

以小鼠脑数据集为例，本文提出的C-Zip 中仅使用CNN 模型，即可达到与DeepZip 相近的压缩比优化效果，并且可以减少预测时间，如图12 所示。

图12 DeepZip 与C-Zip 压缩比与预测时间对比Fig.12 Comparison of DeepZip and C-Zip in CR and predicting time

取数据集中少量数据过拟合训练模型作为整体图像序列的预测模型，压缩结果如表5 所示。对于专用模型压缩以图片为单位的原训练方法和本文提出的以数据集为单位的压缩方法，两者结果较为接近，验证了本文方法在光源图像压缩问题上的有效性。在化石翅膀数据集的结果中，原方法的压缩比较高。在小鼠脑和鱼鳞数据集的结果中，本文方法的压缩比较高，这是因为实际的模型训练过程中，考虑到实际应用的时间限制，训练过程中达到指定epoch 即停止训练，会导致训练过程中未找到最优解的问题，从而导致某些图像压缩效果不佳。本文方法在压缩时随机选取的模型若为训练效果好的模型，则会出现整体压缩比高于原方法的结果，这是未来可以改进的方向。但是相较于传统压缩方法，这两种方法的压缩比均可获得0.5 以上的提升效果。

表5 2 种压缩方式的压缩比对比Table 5 Comparison of CR of two compression methods

4.3 概率距离分析

对不同数据集的图像序列，经过相同的时间差分与分区量化、训练与预测方法，仅将模型输出改为概率距离，算术编码改为分区量化过程，所得压缩比结果如表6 所示。

表6 不同数据集上的概率距离量化结果Table 6 Probability distance quantization results on different datasets

不同数据集概率距离的占位符不同，量化后比特位为7～9 位，相较于原16 位数据，该部分数据在比特位上可以节省43.75%～56.25%的存储空间。结合保留数据占比，整体压缩比为1.74～2.00，与使用概率距离前的压缩方法相比，整体压缩比有所下降。

在单个像素值的概率距离的计算过程中，仅涉及简单的加减运算，相较于算术编码，该压缩流程更易于硬件实现及加速。同时，不同像素值的概率距离计算过程相互独立，后续分区量化过程同为高可并行方法。因此，对比原始压缩流程，概率距离量化流程能够在保证压缩比的前提下提高并行度。

4.4 整体压缩比对比

在本文方法中，为保证压缩过程无损，压缩后需要存储的数据包含预测模型数据、差分量化后保留数据、Rank 保留数据以及Rank 量化后数据4 个部分，其中预测模型数据可忽略不计，另外3 个部分数据大小占原数据大小比值如表7 所示，整体压缩比为1.69～2.22。PNG、JPEG2000、JPEG_LS、FLIF 和本文方法的压缩比对比如表8 所示，相较于传统无损压缩方法，本文方法的压缩比提升了0.23～0.58。可见，本文方法在保证压缩比优化的前提下，具有较高的并行度。

表7 不同数据集上的整体压缩比Table 7 Overall CR on different datasets

表8 5 种方法的压缩比对比Table 8 Comparison of CR of five methods

5 结束语

本文提出一种面向同步辐射光源图像的可并行智能无损压缩方法。通过充分挖掘该类图像序列内部相关性，设计可逆的分区量化方法。以数据集为单位过拟合训练模型，作为概率预测器，并结合稳定的概率距离计算方法，在确保图像压缩比的同时提高了编码并行度。实验结果表明，该方法相比于传统图像无损压缩方法对于同步辐射光源图像具有更好的压缩效果。下一步将细化分区量化中占位符的选择范围，明确占位符对压缩效果的影响程度，形成可量化指标，同时通过提升模型训练过程中寻找最优解的速度，以获得稳定的压缩比优化效果，并且可将该方法与FPGA 等硬件相结合进一步降低计算成本，加速压缩过程，提升适用范围。