合金元素对锆合金氧化膜晶粒演变影响的仿真实验

崔国栋，张程菘，陈大志，赵 毅

（1.西南交通大学材料科学与工程学院，成都 610031；2.西南交通大学宜宾研究院，四川宜宾 644000；3.中国核动力研究设计院反应堆燃料及材料重点实验室，成都 610005）

0 引言

在材料科学与工程领域通过引入计算机模拟仿真技术，具有以下几个方面的特点：①可预测材料可能具备的性能，指明正确的实验方向；②可进一步验证实验结果的准确性；③用模拟得到的参数指导实验，减少实验重复率，节省资源；④可以量化预测材料微结构的演变与性质之间的关系［1-3］。目前，应用于各种微观组织模拟的方法主要有分子动力学方法、蒙特卡洛方法、第一性原理方法和相场方法等。其中，相场方法采用动力学微分方程来表示热力学驱动、有序化、分解、扩散等现象，可直接用来模拟材料微观组织形成过程［4］。

在晶粒演变领域，相场方法应用最早也最成熟。Chen［5］以晶粒的取向作为序参量，构造简单的双势阱自由能函数，建立研究均匀场下晶粒演变的相场模型。以Chen的研究为基础，众多研究者在晶粒演变方面开展了大量的工作，如晶粒长大的Ostwald 熟化现象［6］，应力［7］、第二相粒子［8］与缺陷［9］对晶粒长大动力学的影响等。Xiao等［10］采用两套序参量分别表示原晶粒和再结晶晶粒，实现了材料动态再结晶过程的模拟。Devaraj等［11］建立连续相场模型研究了合金元素对铝合金纳米晶稳定性的影响，发现Mg 在晶界的偏聚可提高纳米晶的热稳定性。将连续相场模型加以改进，采用原子占位几率作为序参量，发展出微观相场方法，用于材料微观组织中元素分布的模拟。Lu 等［12］采用微观相场模型对Ni-Al-V高温合金时效过程进行模拟时发现Ni 原子会在（002）晶面聚集而Al、V 原子在（001）面聚集。

基于以上研究，本实验采用相场方法模拟合金元素对锆合金氧化膜微观组织演变的影响机制。

1 实验设计意义

锆合金的典型组成是超过95%Zr 和低于2%的Sn、Nb、Fe、Cr、Ni 和其他金属，具有高硬度、良好的耐腐蚀性和延展性，主要用途在核技术领域，如作为核反应堆的堆芯结构材料燃料包壳、压力管、支架和孔道管等。锆合金在反应堆中与300 ℃～400 ℃高温水发生反应，极易形成氧化膜，当氧化膜达到一定厚度时会严重影响其耐蚀性，为核反应堆的正常运行带来安全隐患。

锆合金氧化膜的形成、扩展和演变是一个复杂的过程，受合金元素的影响较大。例如，随着烧结温度的升高，Fe和ZrO2逐渐形成Zr6Fe3O 纳米颗粒，导致烧结后锆合金样品的硬度和密度增加［13］；Sn可以促进t-ZrO2向m-ZrO2转变，同时Sn 容易在氧化物晶界处偏聚，导致晶界中孔隙的产生［14］。Nb 在氧化膜中以单质形式存在，随后逐步溶解并转变成不同种类的Nb氧化合物，Nb同时促进共格界面的m-ZrO2柱状晶的形成，有利于腐蚀性能提高［15］。目前虽针对锆合金氧化膜的形成做了一定的研究，但合金元素对氧化膜微观组织演变的影响规律尚不清楚。

2 实验方案

（1）第一性原理计算Fe、Sn、Nb 元素含量对ZrO2结构稳定性的影响以及对韧塑性等力学性能的影响。

（2）考虑缺陷的影响，采用第一性原理过渡态（Transition state，TS）搜索方法及原子跳动模型研究Fe、Sn、Nb原子在ZrO2晶格中的扩散行为。

（3）采用第一性原理方法计算Fe、Sn、Nb原子在ZrO2晶格中的溶解／分离能，用于相场模型相变驱动。

（4）采用热力学计算Fe、Sn、Nb 掺杂ZrO2的自由能，用于相场模型中自由能函数构建。

（5）基于相界面位向关系、晶格错配及微观弹塑性力学构建相场弹性能项，以晶体取向和合金元素含量为序参量建立多成分多相晶粒演变相场模型（Allen-Cahn方程和Cahn-Hilliard方程）。

（6）根据合金元素及含量修正相场参数，建立相场参数与合金元素之间的关系，进行相场模拟，与文献报道实验结果进行对比验证。

第一性原理计算和热力学计算均在Materials Studio 8.0 软件中进行。相场模型构建在MatLab R2021b中完成。

3 计算设置

形成能计算公式如下：

式中：Etot为计算晶胞总能量；EZr、EM、EO分别为Zr、合金元素及O在单质状态下的能量；m、n、p分别为晶胞中Zr、合金元素及O原子的数量；N为合金元素Fe、Sn或Nb（下同）。

溶解能计算公式：

式中：EZrO2+M为含合金元素的ZrO2晶体能量；EZr为Zr元素能量；EZrO2为ZrO2晶体能量；EN为合金元素能量。

分离能计算公式如下：

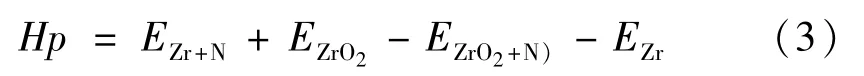
式中：EZr+N为含合金元素的Zr元素能量；EZrO2为ZrO2晶体能量；EZrO2+M为含合金元素的ZrO2晶体能量；EZr为Zr元素能量。

4 实验结果与讨论

4.1 Fe、Sn、Nb元素含量对ZrO2 结构稳定性及性能的影响规律

锆合金在服役过程中主要产生2 种结构的ZrO2，即：立方晶系m-ZrO2和三斜晶系t-ZrO2，在计算时同样只考虑以上2 种结构的ZrO2。依次将晶体结构中的Zr原子用Fe、Sn和Nb原子取代，通过计算ZrO2晶格的形成能表征其热力学稳定性，研究合金元素含量对ZrO2结构稳定性及性能的影响规律。

图1 所示为合金元素掺杂ZrO2形成能随合金元素掺杂量的变化规律，对于未掺杂的2种ZrO2，其形成能非常接近，且为负值，说明2 种ZrO2均能稳定存在，m-ZrO2较t-ZrO2相比更稳定。掺杂合金元素后2种ZrO2的稳定性均发生不同程度的降低，且随着合金元素掺杂比例的提高，形成能逐渐升高，稳定性逐渐降低。3 种掺杂元素中，Fe 对ZrO2稳定性的影响最大，Nb的影响最小，Sn的影响介于二者之间。

图1 ZrO2 形成能随合金元素掺杂量的变化

图2 所示为ZrO2的力学性能随合金元素含量的变化。可见，Sn掺杂使得ZrO2的体模量、剪切模量和弹性模量下降，Nb 和Fe 掺杂提高ZrO2的体模量、剪切模量和弹性模量。尤其Fe 的掺杂提高效果明显。通常采用剪切模量与体模量的比值，即G／B来判断材料的脆性，当G／B ＜0.5，材料表现为塑性特征。由图2（d）可见，t-ZrO2的塑性优于m-ZrO2，尤其当Nb、Sn掺杂后，其塑性进一步提高。ZrO2的脆性特征是导致其开裂剥落的原因，提高其韧性有利于提升氧化膜对锆合金的防护效果。t-ZrO2在辐照条件下容易产生缺陷，导致韧性下降，可通过添加合金元素提高其韧性，进而延长锆合金包壳材料的使用寿命。

图2 ZrO2 力学性能随合金元素掺杂量的变化

4.2 Fe、Sn、Nb对氧扩散的影响

为进一步研究合金元素Fe、Sn、Nb 对O 在ZrO2中扩散的影响。采用第一性原理搜索过渡态的方法进行计算，假设O在ZrO2中的扩散是通过晶格中的氧空位进行的。构造含氧空位的原子扩散始态和终态模型，计算O原子从始态迁移至终态位置路径上的能量变化，即可获得O原子扩散的激活能Q，如图3 所示，在研究合金元素对O扩散激活能的影响时，在氧扩散的路径附近放置合金元素原子。

图3 氧在t-ZrO2 晶格中的扩散

合金元素对O 原子扩散激活能的影响见图4，相对于Zr 合金基体，O 在含空位的ZrO2中扩散激活能明显降低，这说明辐照可能明显促进O原子在ZrO2中的扩散，使得氧化膜厚度明显增厚。与此同时，O原子在t-ZrO2中的扩散易于在m-ZrO2中扩散，t-ZrO2氧化膜对锆合金具有很好的保护作用，在辐照条件下容易产生空位且O原子扩散更快，不利于锆合金构件的防护。Sn、Nb 降低了O 原子在ZrO2中的扩散激活能，促进O 的扩散，尤其对于Sn 掺杂的t-ZrO2，其扩散激活能为负值，说明O 在晶格中自发迁移，快速扩散。对于m-ZrO2，Fe 掺杂后可提高O原子扩散激活能，这说明Fe与O原子之间具有较强的亲和力。

图4 合金元素对ZrO2 中氧原子扩散的影响

4.3 Fe、Sn、Nb 在ZrO2 晶体中的溶解／分离能及热力学自由能

研究合金元素Fe、Sn、Nb 在ZrO2中的分布，可通过计算其在ZrO2晶体中的溶解／分离能得到。通过构造以下反应方程式计算合金元素的溶解／分离能。

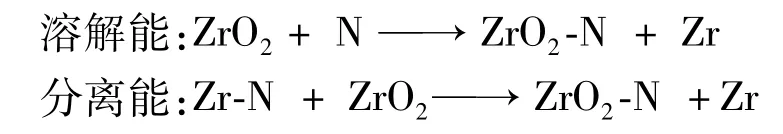
式中：ZrO2-N为含合金元素的ZrO2晶体；Zr-N为含合金元素的Zr。

计算结果显示，无论是溶解能还是分离能均为正值，说明合金元素在ZrO2晶体中难于溶解。通过计算分离能发现，合金元素倾向位于Zr 的基体中，ZrO2中的合金元素含量十分有限，ZrO2中合金元素含量过高会导致晶格失稳，这与前面计算的结果一致。

通过声子谱计算含合金元素（含量为25%）ZrO2的热力学自由能（以形成能为基准，通过第一性原理外推计算），结果如图5 所示。各相自由能变化规律一致，均随温度升高逐渐降低，由此可为ZrO2中合金元素分布模拟提供自由能函数数据。

图5 合金元素掺杂ZrO2 热力学自由能变化情况

4.4 ZrO2 晶粒中Fe、Sn、Nb元素分布相场模型

采用序参量Ci（i＝1，2，…，n）和ηp（p＝1，2，…，n）分别表示ZrO2中合金元素的含量和晶粒取向，以此构建多成分多晶相场模型，用于模拟ZrO2晶粒中合金元素的分布情况。整个体系的化学自由能

式中：f1和f2为局域自由能密度；ηp为晶粒晶体学取向的序参量；n为序参量的个数；Ci为浓度场变量；κi和κc分别为序参量和浓度场变量的梯度能系数；uT是与温度有关的模拟变量，uT＝0～1。不考虑晶粒长大的影响或在体系温度较低时，uT＝0，则

考虑成分变化引起的弹性应变能，体系的自由能表示成化学自由能Fch和弹性应变能Fel之和

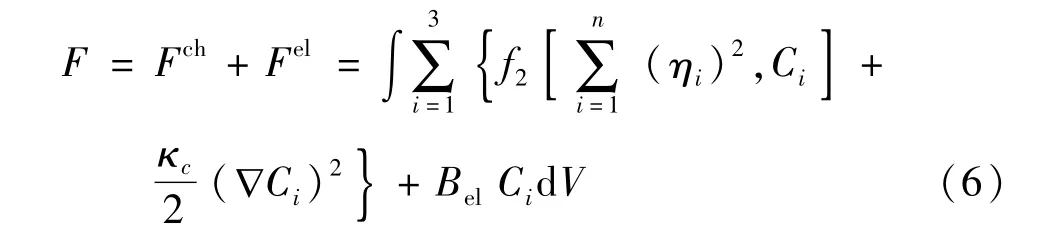
对应于不同的合金元素，取不同的a、b、n值。弹性能采用微观弹性理论描述

锆合金氧化膜微观组织演变通过求解含时金兹堡-朗道方程获得

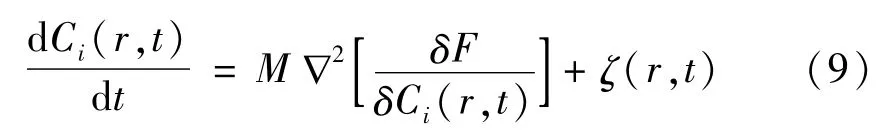
式中：M为原子迁移系数；δ 为变分算子；ζ（r，t）为热涨落项。

求解相场方程时采用半隐式傅里叶变换法求解。

4.5 Fe、Sn、Nb分布相场模拟

基于4.4 节的相场模型，采用第一性原理计算合金元素掺杂后晶格常数的变化，计算结果见表1（假设合金元素含量均小于5 at.%）。根据以上参数进行相场模拟，并与文献［16］中报道的实验结果进行对比（见图6），模拟结果与实验结果吻合较好。对于m-ZrO2，Fe原子（蓝色）由于产生的晶格畸变较大，迅速向晶界迁移以减小晶格畸变带来的弹性应变能；Nb、Sn 2 种元素同时也向晶界迁移，在晶界处形成微小的元素富集区，这些元素富集区会逐渐转变成金属间化合物（例如ZrFe2）或者单质（Nb）。对于t-ZrO2，所有合金元素同时向晶界偏聚，并在晶界处形成合金元素富集的第二相粒子，这与文献［17］中报道一致。

表1 合金元素在ZrO2 晶粒中分布相场模拟唯象参数

图6 合金元素在ZrO2 中分布相场模拟对比

5 结语

在材料科学与工程领域微观尺度，通过计算机模拟技术可预测材料微结构的形成和演变与各项性能之间的关系。本文通过第一性原理计算了Fe、Sn、Nb 等合金元素对ZrO2结构稳定性影响，以及合金原子在ZrO2晶格中的溶解／分离能／自由能，构建了相场自由能函数和晶粒演变相场模型，进行相场模拟并与文献报道实验结果进行比较。通过以上实验项目的开展，揭示了Fe、Sn、Nb等合金元素在氧化膜中分布规律及其对氧化膜微观组织演变的影响机制。通过实验使学生熟悉Materials Studio软件操作，初步掌握MatLab 编程实现晶体结构建模，培养学生运用计算机模拟来解决材料科学与工程领域科研问题，加深学生对材料成分、结构与性能关系的理解，拓宽专业领域，为具备宽厚视野的创新性应用型高素质人才培养奠定基础。