基于深度学习的往复压缩机故障检测方法研究
2023-01-27朱浩玮刘兆增
李 强,王 杰,秦 政,王 尧,朱浩玮,刘兆增
(中国石油大学(华东)新能源学院,山东青岛 266580)
0 引言
往复压缩机故障模式众多[1-2],因而一直是国内外故障诊断学者研究的热点。早期针对往复压缩机的故障诊断主要是依靠专家的现场经验,这种方法的诊断结果具有较高的人为限定性。随着传感器与计算机技术的飞速发展,将往复压缩机振动、压力、电机电流等信号与机器学习算法相结合的故障诊断方法出现[3-4],在实验室研究中取得了不错的诊断效果。Li等[5]通过测量活塞杆应变提出了无损气缸的示功图绘制方法,并基于此提出用于气阀故障诊断的示功图关键特征点重构算法。Wang 等[6]使用图像处理方法获取示功图的7 个不变矩特征,并将该特征用于训练支持向量机的特征向量,实现了往复压缩机气阀的故障诊断。Pichler等[7-8]则将对数示功图膨胀阶段的斜率与压力作为特征参数,用于训练分类器实现气阀的故障诊断。唐友福等[9]基于示功图的几何性质特征,利用BP神经网络作为分类器对压缩机故障进行识别与分类。在工业应用中,Hoerbiger、PROGNOST、Bently Nevada开发的在线监测系统中主要是检测示功图的变化[10]。上述基于示功图的故障诊断研究中,诊断效果主要依赖于特征提取方法的优劣;故障诊断方法依赖于正常与故障状态下的数据,在缺乏故障数据的情况下无法进行故障诊断。由于压缩机故障模式多种多样,而现场的故障数据较难获取,很难收集到所有故障模式对应的数据,使得基于给定特征与传统机器学习算法相结合的压缩机故障诊断方法具有较大的局限性。近年来,随着深度学习在机器视觉领域的兴起[11],依靠强大的学习性能,深度学习模型可以从原始信号中直接提取特征,并通过训练实现数据分类。杨洪柏等[12]将气阀正常与故障状态下的原始振动信号作为输入,利用卷积神经网络对信号特征进行提取,获得了较高的故障识别率。但该种方法同样依赖于故障数据集,这也是限制卷积神经网络广泛应用于机械设备故障诊断的重要原因之一。
为了摆脱卷积神经网络应用于故障诊断时过度依赖于故障数据集的问题,同时解决人为提取特征的冗余性与不足性,本文以往复压缩机示功图为研究对象,提出了基于AlexNet卷积神经网络的压缩机运行工况分类模型,并通过对分类模型全连接层一维特征向量的处理,提出了故障检测算法。以AlexNet 卷积神经网络为基础架构的故障检测模型基于正常数据集进行训练,利用卷积神经网络(CNN)对示功图自动提取特征,通过实验验证并判断是否存在异常。
1 故障检测方法
本文以AlexNet 卷积神经网络为原型,以往复压缩机示功图为故障检测对象,搭建基于AlexNet 卷积神经网络的故障检测模型。
1.1 AlexNet卷积神经网络
AlexNet 是由Hinton 和Alex Kri-zhevsky 等[13]提出的卷积神经网络模型,它共有8 层带权重的网络层,包含5 层卷积层Ci(i=1,2,…,5)(其中第1、2、5 层卷积层后各包含1 层最大池化层)和3 层全连接层FCi(i=6,7,8)。与传统神经网络方法相比,AlexNet采用ReLU激活函数改善了梯度消失及收敛波动问题,同时,通过引入DropOut方法控制过拟合[14]。基于上述特点与优势,本文选择AlexNet 为基本分类模型通过修改模型结构搭建故障检测模型。同时,根据本文研究对象的复杂程度对原网络结构进行了部分精简,缩减了卷积核数目与全连接层的神经元数目。本文使用精简后的网络结构与相关参数如图1 所示。

图1 AlexNet卷积神经网络结构
1.2 卷积神经网络模型
本卷积神经网络模型由图像输入、卷积层与池化层、全连接层与输出层以及优化器与损失函数组成。
(1)图像输入。往复压缩机的示功图反映了压缩机的运行状态以及工作特性,它对气阀、活塞组件等常见故障较为敏感,故选择示功图作为故障检测对象。通过键相传感器识别压缩机运行过程、压力传感器测量气缸动态压力的方法实测的示功图如图2 所示。

图2 往复压缩机示功图
本文采用卷积神经网络进行特征提取时,图2 所示示功图的横纵坐标刻度、标签与压缩机运行过程无关,为辅助说明信息而非特征信息,在生成图片数据集时去除该类信息,仅保留与压缩机运行过程有关的示功图形状信息。此外,对比图2(a)与(b)可以发现,在具有不同排气压力的工况下采用相同的纵坐标会导致排气压力较低工况的示功图中出现大面积空洞,若不加处理,空洞特征也将作为主要特征被训练与学习,从而影响模型训练精度与使用效果。故在预处理时,将纵坐标进行归一化处理,

此外,为了增加示功图形状与背景的对比度,将示功图进行二值化处理。如图3 所示为预处理后的示功图。

图3 预处理后的示功图
(2)卷积层与池化层。卷积层的目的是将输入图片的主要特征进行提取,AlexNet 网络具有5 层卷积层,卷积核大小与步长分别为:C1=11 ×11,S1=4;C2=5 ×5,S2=1;C3=C4=C5=3 ×3,S3=S4=S5=1。卷积运算式为

式中:y(i,j)为卷积运算结果矩阵中的元素;A为图像经数字采样后获得的数字矩阵;K为卷积核;k为卷积核大小;i,j分别为矩阵中行、列的索引。
卷积运算后的结果需要进入激活函数进行计算,AlexNet网络采用ReLU函数作为激活函数

在池化层运算中,通过采用下采样的方法降低特征图维度,对图片的特征进一步提取,并减少参数。不同于其它的网络模型,AlexNet使用的池化(Pooling)是可重叠的,在池化过程中,每次移动的步长小于池化的窗口长度。池化的大小为3 ×3 的正方形,每次池化移动步长为2,与非重叠方案池化大小为2 ×2,步长为2相比,输出的维度是相等的,但重叠池化能在一定程度上抑制过拟合,即:

式中:y为数字矩阵;i,j分别为矩阵y中行与列的索引;λ为池化移动步长;l为池化区域长度;w为池化区域宽度。
(3)全连接层和输出层。AlexNet 网络具有3 层全连接层FCi(i=6,7,8),FC6与FC7神经元数量均为2 048,本文设为1 024,Dropout 比例均为0.2,FC8为采用softmax 函数作为激活函数的全连接层,softmax分类器是logistic二类分类器的一个泛化,可实现多类别分类[15]。最终输出多类样本标签的概率分布。FC8全连接层的第i个神经元的输出

式中:N为FC8全连接层的神经元数量,同时也是样本类别数量;Vi和Vj为FC8全连接层中的第i个和第j个神经元。
(4)优化器与损失函数。优化器将计算的损失函数的梯度应用在模型训练计算的变量更新中,不断对模型参数进行迭代更新,直到循环次数达到预设值。本文采用学习率自适应的Adam 进行权值参数优化,通过式(5)得到样本m的第i个神经元的softmax 值pm,i并与反映样本m与类别i的从属关系函数lm,i求取交叉熵,作为损失函数

式中:M为样本的数量;lm,i为样本m的实际类别函数,当样本m属于类别i时取1,否则取0。
1.3 分类模型训练
本文的分类模型训练流程包括:数据集采集、前向传播求误差、反向传播更新网络参数以及模型测试。
(1)数据集采集。通过往复空气压缩机实验测试平台采集正常工作状态下各个工况的示功图,并去除图片中的辅助说明信息,形成带有各个工况标签的数据图集I。
(2)前向传播求误差。将每个标签的样本集按比例随机分成训练集、验证集和测试集。为了加快参数更新速度,将数据图集I随机划分为多个小批量样本组,每个样本组包含b个样本,初始化网络参数、学习率ε,Dropout 比率,每次从训练集中选择小批量b个样本进行卷积、池化、全连接运算,求取最终的softmax输出值,并根据式(6)求取损失函数。
(3)反向传播更新网络参数。基于前向传播的损失,利用Adam算法迭代更新网络参数,直至一个批量样本组循环结束。然后,在样本集中再依次选择b个不同样本,重复上述小循环,直至循环完成所有样本。在训练过程中,每轮循环结束时,使用验证集验证网络的分类效果,若模型具有良好的分类性能,则将当前的网络参数保留,否则对网络参数进行调整。
(4)模型测试。使用预留的测试集样本对网络的泛化能力进行测试,若模型分类性能达标,则将此时的网络参数作为后续故障诊断模型的结构参数,反之,调整Dropout比率。
1.4 故障检测算法实现
压缩机正常工作情况下各个工况的示功图特征被卷积神经网络识别与学习后得到压缩机运行工况分类模型,该模型可以很好地提取示功图特征,并将不同运行工况下的示功图特征差异化,基于该特点,本文利用AlexNet分类模型作为主干特征提取网络,通过共享网络权值,对比同一特征提取网络下全连接层的输出,将压缩机运行工况识别的多分类模型转化为故障检测的二分类模型。
当示功图样本m输入至已训练好的N分类模型后,经卷积、池化与全连接,示功图特征被提取与高度压缩,最终在全连接层中输出一维特征向量F=[f1,f2,…,fi,…,fN],对于同一类样本经相同的特征提取网络处理后获得的一维特征向量F的分量大小、分布相近,而不同类样本间或异常样本与正常样本间差异较大。本文基于该特征向量的特点构建异常检测算法:①将2 个一维特征向量作差并取绝对值,获得;②提取ΔF的最大分量Δfi,并将上述最大分量输入sigmod 函数中,将其映射至(0,1)之间,并将其定义为差异度ΔS(如式7);③将差异度与给定的阈值ρ 作比较,判断样本是否存在异常。即当sigmod(Δfi)小于ρ 时判断样本为正常,否则为异常:

上述故障检测算法是基于样本间的特征向量的差异展开,涉及实际样本与参照样本之间的比较,对于同一类样本,其间一维特征向量差异较小,但考虑总体特征表现,将每一类训练集中的所有正常样本的特征向量进行平均处理,获得每一类平均化后的特征向量。由于不同类样本间特征向量差异较大,引起的差异度较大,可能会产生超过阈值引起误判的现象,故本文采用计算两特征向量L1 范数(如式8)的方法先进行类别匹配,再计算差异度。

式中,fa,i与fd,i分别为平均化后的参照样本工况a与实际待检样本工况d的一维特征向量的第i个分量。
L1 范数相当于求取了2 个一维向量的距离,实际待检样本特征向量与各类样本平均化后的特征向量的L1 范数越小则归属关系越强烈,即使是故障样本也是在某1 工况下发生的,虽然特征向量与正常工况差异较大,但特征向量分布仍与故障前工况相近,其与故障前正常工况的L1 范数最小,也可实现类别匹配。匹配完成后,计算实际待检样本与该类别的差异度并与阈值ρ作比较进行异常样本检测。具体异常检测算法流程如图4 所示。

图4 异常检测算法流程
2 实验与分析
2.1 实验装置
本文基于往复压缩机性能测试实验的示功测试原理,通过改装单级无油润滑往复空气压缩机搭建了实验测试装置。实验装置由往复压缩机、低压直流电源、压力传感器、键相传感器、数据采集卡等硬件与数据采集软件2 部分组成,硬件主要参数:往复压缩机的排气压力范围为0~0.8 MPa,转速为1 440 r/min;低压直流电源为双通道输出,电压输出范围为0~36 V;压力传感器量程为0~1 MPa,0~10 V 信号输出,精度为±0.5%FS;键相传感器为旋转编码器,5 V 脉冲信号输出,分辨率为360 P/R;数据采集卡采用NI 数据采集卡,单端32 通道,ADC 分辨率16 Bit。实验装置如图5 所示。

图5 实验装置
为测量气缸动态压力:①在气缸压板上开孔将气缸内气体压力引出并与压力变送器连接获得与压力成正比的电压信号;②为了将气缸动态压力与压缩机工作过程相对应,以曲柄转角为中间变量,将360 P/R的三相增量型旋转编码器作为键相传感器,将Z相起点与活塞上止点对应,作为每周期压力信号采样起点,利用A相等角度发射脉冲信号的特性触发压力信号采样;③通过调节压缩机排气阀调节排气压力,以改变压缩机工况。本实验选择4 个排气压力分别为0.3、0.4、0.5、0.6 MPa 工况下的示功图作为训练数据集,设置数据采集卡采样频率为8 640 Hz,每次采集1 个工况下压缩机单个工作周期的360 个气缸动态压力数据点,连续采集230个周期,共计920 个样本,组成样本集,每个工况数据中取170 个样本按照14:3 的比例随机分为训练集和验证集,剩余的60个样本用于测试。
2.2 故障模拟
本文在往复式压缩机故障模拟试验装置上对故障检测模型的准确性进行了验证,按上述预定的4 个工况排气压力的吸、排气阀泄漏故障进行模拟,获取故障数据集作为测试集。实验使用的压缩机气阀为舌簧阀,本文通过在舌簧阀片上开直径为1 mm 的圆孔作为泄漏孔实现故障的模拟,如图6 所示。调节压缩机排气阀,使压缩机分别在上述4 个工况下稳定工作,按设定的采样率,在每个工况下采集压缩机单个工作周期的气缸动态压力数据点,每个工况采集60 个周期。最终获得的数据集数量:①正常情况运转时,测试4个工况,训练样本数分别各为140 个、验证样本数量分别各为30 个、测试样本数量分别各为60 个;②模拟故障运转时,测试4 个工况,测试样本数量分别各为60 个。

图6 舌簧阀泄漏故障模拟
2.3 模型训练参数寻优
在模型训练中影响训练速度与准确率的参数有Adma的学习率(ε)、批尺寸大小(batch_size)。为寻找最佳参数,遵循单一变量原则对各个参数取不同值,研究其训练精度的变化趋势,变化曲线如图7 所示。
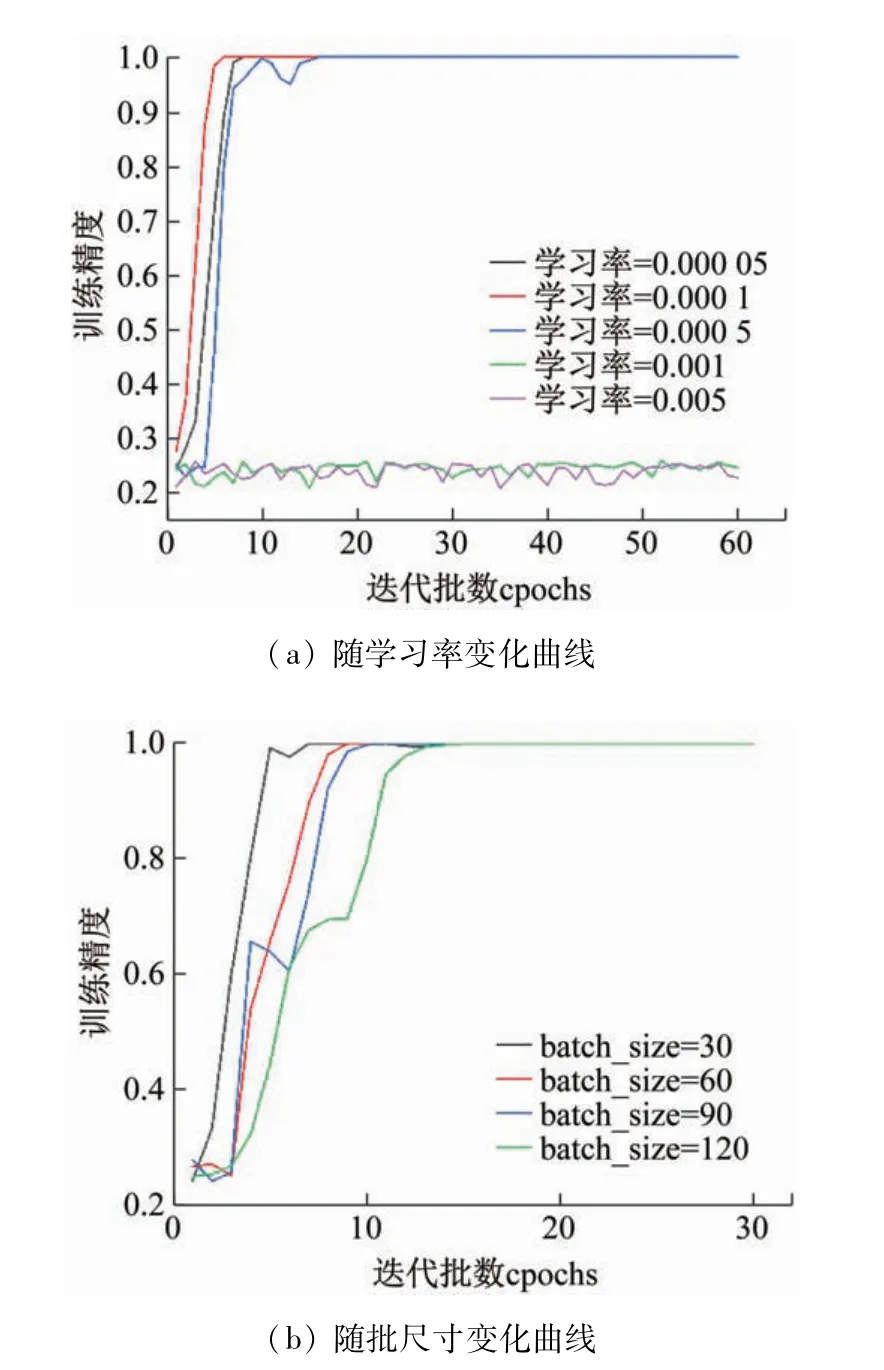
图7 训练精度的变化趋势图
图7(a)为批尺寸batch_size =32 的训练精度随学习率变化曲线,由图可以看出,当学习率为0.000 1时,训练精度最先稳定并达到最大值。当学习率减小时,训练精度收敛速度变慢;当学习率增大时,训练精度产生波动,并逐渐降低。图7(b)为学习率ε =0.000 1 的训练精度随批尺寸大小变化曲线,由图可以看出,达到最优训练精度所需的迭代批数随着批尺寸的增大而增加,但由于批尺寸的不同,每个迭代批数中的迭代次数不同,批尺寸大小分别为30、60、90、120时,达到稳定的最大训练精度所需的迭代次数分别为252、81、66、60,故当批尺寸大小为120 时,可以以最少的迭代次数达到最优的训练精度,该批尺寸大小也是验证集所能达到的最大值。因此,为了获得较高的训练精度,将优化器的学习率设置为0.000 1,批尺寸设置为120。
3 模型性能试验
为了对本文提出的故障检测模型进行测试,随机选择了未用于模型训练的正常测试数据集与故障测试数据集样本各40 个,建立混淆矩阵,计算准确率、精确率、召回率与F1 值,评价模型性能。
3.1 故障示功图对比
将吸、排气阀泄漏故障下的归一化示功图与正常状态下的归一化示功图进行对比,对比情况如图8所示。
由图8 可知,压缩机的运行状态发生变化时,在示功图上主要体现在压缩线和膨胀线的斜率变化,以及进、排气线的长短变化:①当压缩机吸气阀发生泄漏时,由图8(a)可知,压缩气体从吸气阀泄漏,压缩线变得平缓,斜率的绝对值下降,排气过程线缩短,同时,气体在气阀未开启时便可进入气缸,导致膨胀过程被加快,进气过程延长;②当排气阀泄漏时,由图8(b)可知,高压的气体进入气缸,压缩线变得陡峭,斜率的绝对值变大,排气阀提前打开,排气过程延迟,同时,高压气体不断进入气缸,导致膨胀过程延长,进气过程缩短。由上面的图谱也可以发现,压缩机发生轻微故障时,虽然图谱曲线形状会发生变化,但变化并不大,依赖人工进行故障检测,具有一定难度,而采用卷积神经网络则可以很好地捕捉图像变化。
3.2 异常检测结果
将上述正常与故障状态下的示功图样本输入异常检测模型,模型将返回每个样本与相似类别的正常样本间的差异度,当差异度大于等于阈值时则判断为异常,反之,正常。设定不同的阈值,建立如表2 所示的混淆矩阵(其中,TP(True Position)为真阳性、FP(False Position)为假阳性、FN(False Negative)为假阴性、TN(True Negative)为真阴性),从而计算出指标:准确率Acc =(TP+TN)/(TP+TN+FP+FN)、精确率Precision =(TP)/(TP+FP)、召回率Recall =(TP)/(TP+FN)、F1 值F1 =(精确率×召回率×2)/(精确率+召回率),作为模型可靠性评价标准。
图9 为评价指标随阈值的变化曲线,由图可知,随着阈值的提高,模型容错能力下降,精确率下降,准确率、召回率与F1 值均有所提高。当阈值为80%时,在正常数据与故障数据各40 条的情况下:预测正确的正常样本为36 个,预测错误的正常样本为4 个;预测正确的异常样本为39 个,预测错误的异常样本为1 个。模型的准确率为93.75%,精确率为97.30%,召回率为90%,F1 值为93.51%,模型取得了很好的预测效果。同时,通过图9 也可以发现,阈值在80%~90%之间时,模型的准确率均在90%以上,这说明模型可以在阈值波动较大的情况下仍保持较好的效果。而在实际运用时,阈值可以根据正常测试样本的差异度平均值,并考虑一定的容错裕度进行设定,并且在使用过程中不断修正,使得模型的使用效果达到最优。
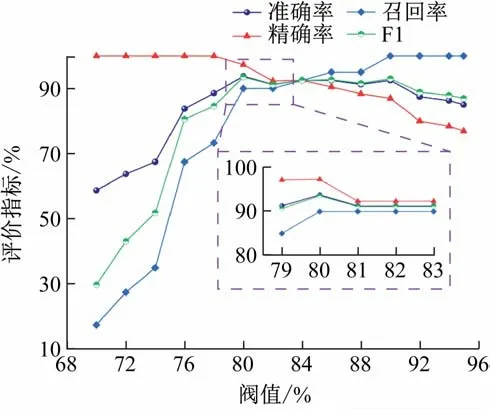
图9 评价指标随阈值的变化曲线
4 结论
本文提出的基于卷积神经网络的往复压缩机故障检测模型,以往复压缩机示功图为诊断对象,利用卷积神经网络(CNN)进行特征提取,通过对比样本特征之间的差异进行故障检测。同时,通过搭建的往复空气压缩机实验测试装置,对进、排气阀泄漏故障进行模拟测试,结果表明:在仅有压缩机正常运行数据的情况下,可以很好地完成往复压缩机热力性能故障的检测,当故障评判阈值为80%~90%之间时,模型的故障识别准确率可达90%以上,可进一步对故障气缸进行定位,为故障早期快速报警奠定了基础。同时,该压缩机故障模拟实验也可用于过程流体机械课程的教学实验或本科生的自主开放实验。
