加权源伪抛物型方程解的爆破时间的上下界

伍日广，钟延生

(福建师范大学数学与统计学院，福建 福州 350117)

本文研究了以下初始边值问题解的爆破时间的上下界估计

(1)

众所周知，非线性伪抛物型方程常见于对流体动力学、热力学和过滤理论等各种问题的研究中，文献[1]研究了方程

ut-△ut-△u=a(x)f(u)，

(2)

在狄利克雷(或诺伊曼)边界条件下的爆破时间与爆破速率的上下界估计.此类方程具有广泛的物理背景和丰富的理论内涵，并且可以看作是通过添加色散项△ut的加权源半线性热方程的正则化.文献[2]则考虑了下列问题

(3)

同样也对其相应的爆破界进行了估计.本文的研究受文献[1]启发，在非线性扩散、非线性反应和非线性吸收的多重作用下，将估计问题(1)解的爆破时间上下界.关于抛物型方程解的爆破时间界的问题，可参考文献[1-9].

1 爆破时间的上界估计

在本节中，将分别建立关于狄利克雷边界条件和诺伊曼边界条件下问题(1)解的爆破时间上界的一些估计.

1.1 狄利克雷边界条件

为了得到本小节的结果，首先假设:

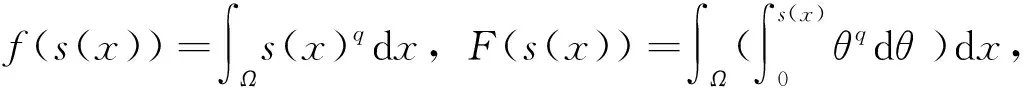
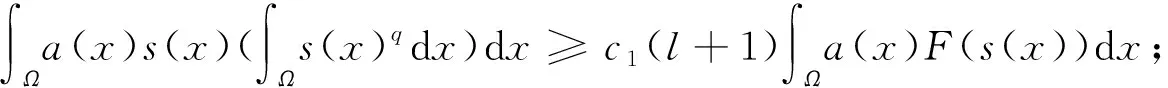
然后，定义辅助函数

(4)

定理1假设条件a1(或a2)、f1、f2、g1成立，u是狄利克雷边界条件下问题(1)的解.则解u在t=t*时以H1范数爆破，并给出了爆破时间t*的一个上界

(5)

证明 首先对辅助函数(4)关于变量t求偏导，再利用(1)中的第一个式子，则可得

(6)

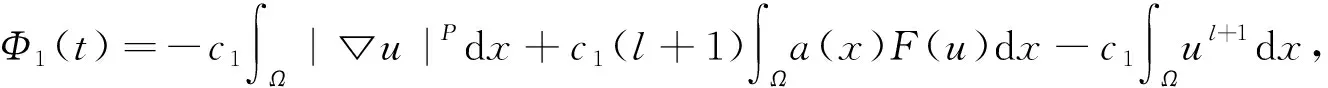
(7)

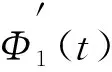
(8)

再利用施瓦兹不等式和杨氏不等式，可得

(9)

(10)

(11)

将式(9)-(11)代入式(8)中可得

(12)

因此，上述式(12)意味着

(13)

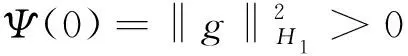
(14)

则对于式(12)，有

(15)

再对式(15)在0到t进行积分，可得

(16)

因为Ψ′(t)>Φ1(t)，所以

(17)

同样对式(17)在0到t进行积分，可得

(18)

显然，式(18)不可能在所有时刻都成立.因此，u的H1范数在某一有限时间t*爆破且

(19)

则定理得证.

1.2 诺伊曼边界条件

在本节中，将建立关于诺伊曼边界条件下问题(1)解的爆破时间上界的一些估计.为了得到本小节的结果，首先定义辅助函数

(20)

定理2假设条件a1(或a2)成立，u是诺伊曼边界条件下问题(1)的非负解.则u在t=t*时,以L1范数爆破，并给出了爆破时间t*的一个上界

(21)

证明 首先对辅助函数(20)关于变量t求偏导，并利用问题(1)中的第一个式子，可得

(22)

则由杨氏不等式

(23)

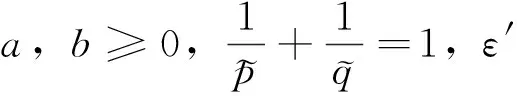
(24)

再利用霍尔德不等式，可得

(25)

对式(25)进行0到t*上的积分，则爆破时间的上界为

(26)

2 爆破时间的下界估计

在本节中，将建立关于狄利克雷(或诺伊曼)边界条件下问题(1) 解的爆破时间下界的估计.为了得到本小节的结果，首先定义辅助函数

(27)

定理3假设条件a1(或a2)成立，u是狄利克雷(或诺伊曼)边界条件下问题(1)的非负解.则解u在t=t*时,以H1范数爆破，并给出了爆破时间t*的一个下界

(28)

证明 首先对辅助函数(27)关于变量t求偏导，并利用问题(1)中的第一个式子，可得

(29)

再利用霍尔德不等式，可得

Ψ′(t)≤K2Ψ(t)q-K3Ψl,

(30)

其中

(31)

最后在0到t*上对式(30)进行积分，可得

(32)

则式(32)为爆破时间的下界.