非自治Schrödinger-Bopp-Podolsky系统的基态解①

贾春容， 李麟，2

1.重庆工商大学 数学与统计学院， 重庆 400067； 2.经济社会应用统计重庆市重点实验室， 重庆 400067

本文主要研究非自治Schrödinger-Bopp-Podolsky系统基态解的存在性：

(1)

其中a>0，K(x)和b(x)满足条件：

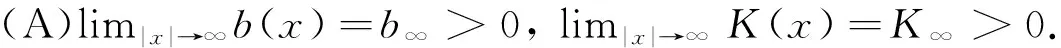
近年来， Schrödinger-Bopp-Podolsky(简称SBP)系统受到越来越多的关注． 文献[1]证明SBP系统解的存在性与不存在性依赖于参数p和q； 随后文献[2]通过纤维法证明当q足够大时， SBP系统没有解； 当q足够小时， SBP系统有两个镜像解； 文献[3]使用Pohozaev-Nehari流形的方法证明非线性项临界增长的SBP系统存在基态解． 目前只有关于SBP系统自治的研究， 如文献[3-6]， 未考虑非自治的情况． 受文献[7-8]的启发， 发现K(x)和b(x)对系统有影响． 本文利用文献[8]中的思想来研究非自治SBP系统的基态解． 变分方法是一类很重要的方法， 已经在其他问题上用这个办法解决了很多问题[9-11].

本文通过建立紧性引理和使用Nehari流形的方法去找SBP系统的基态解． 为得到基态解的存在， 对K(x)和b(x)给出如下假设条件：

(B) 对所有的x∈R3有K(x)≤K∞，b(x)≥b∞成立， 且b(x)-b∞>0在一个正可测集上.

本文主要结果如下：

定理1如果满足条件(A)和(B)， 则系统(1)有一个基态解.

注1本文主要在R3中讨论SBP系统基态解的存在， 最大的困难在于我们无法在全空间R3中得到嵌入紧性． 为了克服障碍我们利用分裂引理恢复有界Palais-Smale序列的紧性． 同时为了找到方程对应能量泛函的临界点， 我们将通过限制在一个Nehari流形上， 然后寻找最小能量解． 文献[12]已经证过Nehari流形上的解， 就是原问题的基态解.

本文根据文献[1]中的方法， 首先对系统的第二个方程进行约化， 变成单变量方程， 系统(1)约化后的单变量方程如下：

-Δu+u+K(x)φK，uu=b(x)|u|p-2u在R3中

(2)

然后给出包含N的主要性质的引理.

引理1

(i) N是一个C1正则流形同构于H1(R3)的一个球；

(ii) 在N上， 存在C2∈R， 有u∈N， 使得J(u)>C2>0；

(iii)u是J的一个自由临界点当且仅当u是J限制在N上的临界点.

‖un‖≥C>0

(6)

因为J是一个C2(H1(R3)， R)泛函，G是一个C1泛函， 则由(6)式推出

(7)

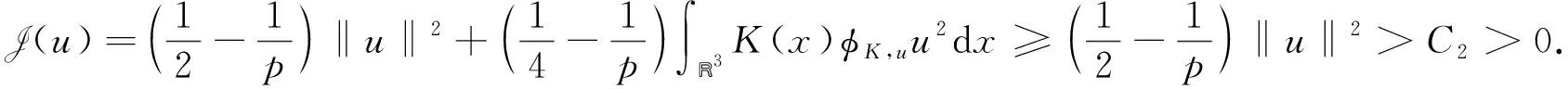
(iii) 与文献[7]中的引理3.1(3)的证明一样.

设m： =inf{J(u)：u∈N}． 由引理1中(ii)知，m是一个正常数． 由引理1中(i)知， 任意的u∈H1(R3)对应(唯一)一个t(u)>0， 使得 J(t(u)u)=maxt(u)>0J(t(u)u)成立.

(8)

证与文献[1]中引理4.5证明类似， 此处省略证明过程.

命题1存在w∈M， 使得I(w)=c成立.

现回到方程(2)， 基于J的临界点的研究， 通过考虑(1)式的(PS)序列的情况， 得出如下引理.

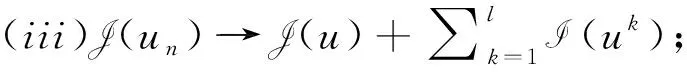
(iv)uk是方程(8)的非平凡解． 若l=0， 则(2)式存在一个解u.

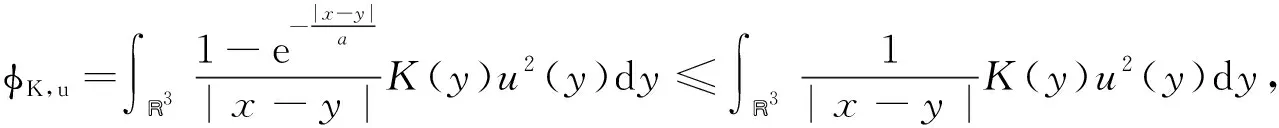
推论1设{un}是一个(PS)d序列， 则对所有d∈(0，c)， {un}是相对紧的.

利用上述已证引理， 现给出定理1的证明.

定理1的证明为求证定理1， 由推论1可知， 现只需证明m0使tw∈N． 因为tw∈N，w∈M和(B)成立， 则

即w∈N， 有I (w)=c． 所以w∈N是J的一个临界点， 故由引理1(iii)知，w是J的一个自由临界点， 最后得出(w，φK， w) ∈H1(R3)×D是(1)式的一个基态解.