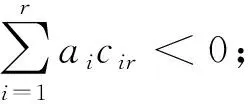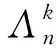二元对称多项式空间的幂和基①

倪雨晴， 李雪珊

西南大学 数学与统计学院， 重庆 400715

给定正整数k， 设f(x)=f(x1，x2， …，xk)是域K上的一个多项式， 若对{1， 2， …，k}的任意一个排列ω， 有

f(x1，x2， …，xk)=f(xω(1)，xω(2)， …，xω(k))

则称f(x)是一个k元对称多项式． 令Λk为所有k元对称多项式构成的向量空间， 则

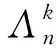
首先， 给出一些基本概念及记号.

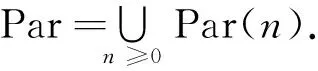
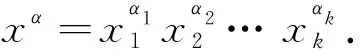
其中α取遍λ的所有不同排列.

对正整数i， 定义

及

给定分拆λ=(λ1，λ2， …，λl)， 定义初等对称多项式eλ=eλ1eλ2…eλl， 完全齐次对称多项式hλ=hλ1hλ2…hλl以及幂和对称多项式pλ=pλ1pλ2…pλl.

命题1[8]对任意正整数n，

{mλ：λ|-n，l(λ)≤k}

(1)

{eλ：λ|-n，λ1≤k}

(2)

{hλ：λ|-n，λ1≤k}

(3)

{pλ：λ|-n，l(λ)≤k}

(4)

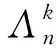
注文献[8]的推论7.8.2实际给出的是(1)，(2)，(3)式以及

{pλ：λ|-n，λ1≤k}

(5)

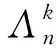
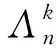
证由文献[8]的推论7.7.6，

其中对λ=〈1j12j2…〉|-i， 有zλ=1j1j1!2j2j2!…，ελ=(-1)i-l(λ)． 由对称多项式基本定理知， {e1，e2， …，ek}是Λk的代数独立生成元， 所以{p1，p2， …，pk}是Λk的生成元． 因此

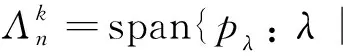
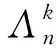
定义1给定正整数n， 设A是Par(n)的子集， 若

{pλ(x1，x2， …，xk)：λ∈A}

(6)

线性无关(相关)， 则称A是k-线性无关(相关)的． 记

p(n，k)=#{λ：λ|-n，l(λ)≤k}

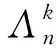
由命题1及命题2知

s1(n，k)={pλ(x1，x2， …，xk)：λ|-n，l(λ)≤k}

及

s2(n，k)={pλ(x1，x2， …，xk)：λ|-n，λ1≤k}

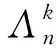
s(n，k)={pλ(x1，x2， …，xk)：λ|-n}

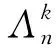
(7)

即p(1， 1， 1， 1)(x1，x2)，p(2， 1， 1)(x1，x2)，p(3， 1)(x1，x2)线性相关.

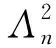
pμ∪(1， 1， 1， 1)(x1，x2)=3pμ∪(2， 1， 1)(x1，x2)-2pμ∪(3， 1)(x1，x2)

因此s(n， 2)的任意包含{pμ∪(1， 1， 1， 1)(x1，x2)，pμ∪(2， 1， 1)(x1，x2)，pμ∪(3， 1)(x1，x2)} 的p(n， 2)元子集都是线性相关的． 更一般地， 我们有：

命题3设A是Par(n)的一个p(n，k)元子集， 若存在μ∈Par， 及A′⊆Par， 使得A′是k-线性相关的， 且{λ∪μ：λ∈A′}⊆A， 则A也是k-线性相关的.

定理1设A⊆Par(n)， 令

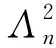
证对正整数n， 有

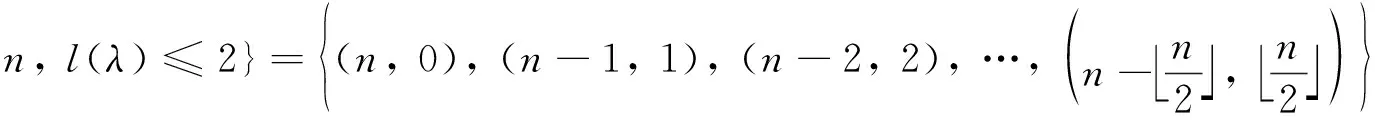
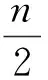
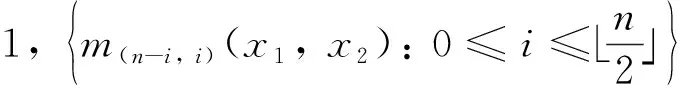
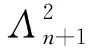
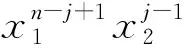
以下用反证法证明当n=2r-1时，A′也线性无关． 若不然， 则存在常数a1，a2，…，ar， 使得

(8)

一方面， 考虑到

因此我们有

(9)

另一方面， 设λ*=〈2m24m4…2rm2r〉， 则我们有

(10)

将(9)，(10)式代入(8)式并比较m(n+1-j， j)(0≤j≤r)的系数得如下r+1个等式：

(11)

由前r个等式， 有