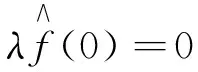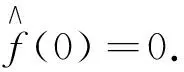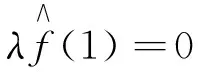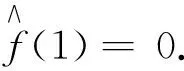Hardy空间上的Volterra-复合算子①

丁宣浩， 邵长慧， 李永宁

1.重庆工商大学 数学与统计学院， 重庆 400067； 2.经济社会应用统计重庆市重点实验室， 重庆 400067

本文中记D为复平面上的单位圆盘， ∂D为单位圆周． 单位圆盘上的Hardy空间[1]H2定义为： 由单位圆盘上的解析函数所构成的Hilbert空间． 设L2(∂D)为单位圆周上的Lebesgue平方可积函数全体， Hardy空间的另一常用定义为

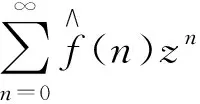
Volterra算子是算子理论中一类重要的有界线性算子， 在很多数学分支， 例如线性微分方程的初值问题、 优化、 种群动态等问题上有着重要应用． Hardy空间H2上的经典的Volterra算子定义为

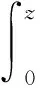
该算子是紧的、 拟幂零的， 没有特征值且谱集只有零点的线性算子[3]． 文献[4]给出了Hardy空间上Volterra算子的不变子空间的刻画：M是V的不变子空间当且仅当M=znH2(D)， 这里n∈N． 这之后， 文献[5]研究并解决了定义在Hp空间上的Volterra型积分算子

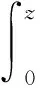
的有界性和紧性的刻画问题， 紧接着， 文献[6]给出了该算子在Bergman空间上的有界性和紧性的充要条件． 随后， 文献[7]给出了该算子在BMOA空间上的有界性和紧性的完全刻画． 文献[8]研究了单位圆盘Hardy空间上的复Volterra算子的不变子空间问题.

Cφf(z)=f∘φ(z)f∈H2

称为H2上的由φ导出的复合算子[9]． 复合算子是解析函数论与算子理论相结合的产物， 它是泛函分析中一类十分有趣的具体算子， 其研究推动着算子理论的发展， 并在动力系统、 遍历理论、 解析函数论等数学领域中有着重要的应用． Hardy空间上复合算子的研究涉及算子理论与解析函数中许多经典结果之间的联系， 目前该类算子的研究已经取得比较系统的理论成果． 关于不同函数空间上的复合算子的范数、 有界性、 紧性、 谱、 Schatten类的结果可参见文献[9-12].

文献[11]用Berezin变换的方法研究了广义Fock空间的Volterra算子与复合算子乘积的有界性、 紧性、 Schatten-p类性质及本性范数估计． 这激发了我们引入Volterra-复合算子Vφ， 其定义为

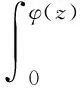
由该算子的定义可知Vφ=CφV， 这是我们将Vφ命名为Volterra-复合算子的一个原因.

文献[13-14]研究了Hardy空间上Volterra算子的其他性质． 关于Hardy空间上算子理论的研究， 虽然已经有超过60年的历史， 但仍焕发着勃勃生机． 本文的第一、 第三作者和其他人合作分别研究了Hardy空间及其子空间上的一些算子的性质[14-16]， 这些结果对于研究其他函数空间上的算子理论有着积极作用.

在本文中， 记σ(Vφ)为Volterra-复合算子Vφ的谱． 设T是Rn上的线性变换， 则T的核定义为

ker(T)={X∈Rn：T(X)=0}

本文安排如下： 首先， 回顾了Volterra算子和复合算子的研究结果， 并引入了Volterra-复合算子Vφ的定义； 在第一节， 刻画Vφ的有界性、 紧性、 核等一些基本性质； 在第二节， 给出Volterra-复合算子Vφ的特征值和奇异值.

1 基本性质

本节主要讨论Volterra-复合算子Vφ的有界性、 紧性以及核的刻画， 给出了3个定理.

下述结论给出了Volterra-复合算子的范数估计：

证因为Vφ=CφV， 并且对∀f∈H2，f有幂级数展开式

将f(z)代入Vf(z)， 则有

特别地， 因为

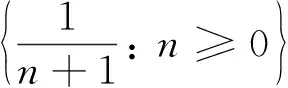
这样便有了

‖Vφ‖=‖CφV‖≤‖Cφ‖‖V‖=‖Cφ‖

又由引理1可知

从而可以得到

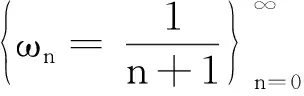
证设f∈H2， 使得

Vφf=0

即

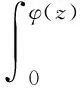
两边同时对z求导， 则可得f(φ(z))φ′(z)=0． 由于φ是非常值函数， 所以φ′(z)≠0， 从而f(φ(z))=0， 即f|φ(D)=0． 又因为φ(D)⊆D且f为解析函数， 由解析函数的零点定理知， 对z∈D， 恒有f(z)=0， 从而kerVφ={0}.

2 特征值与奇异值

本节主要讨论了Volterra-复合算子Vφ的特征值和奇异值问题.

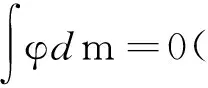
定义1设H是可分的Hilbert空间，T是H上的有界线性算子， 若对λ∈C， 存在非零向量x∈H， 使得Tx=λx， 则称λ是T的特征值， 称x是T的对应特征值λ的特征向量.

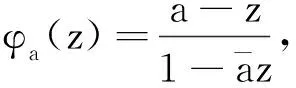
证假设λ≠0是Vφa的特征值， 则存在非零函数f∈H2， 使得Vφaf=λf， 即

CφaVf=λf

首先等式两边作用复合算子Cφa， 可得

CφaCφaVf=λCφaf

注意到

CφaCφa=I

从而

Vf(z)=λf∘φa(z)

(1)

再将V作用于等式(1)的两边， 由φa∘φa(z)=z可得

V2f(z)=λVf∘φa(z)=λ(λf∘φa∘φa(z))=λ2f(z)

(2)

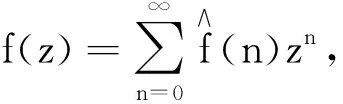
代入(2)式， 得

(3)

比较(3)式中左右两端z的系数， 则

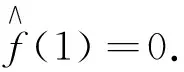
同理比较(3)式两端z2的系数， 可得

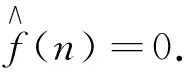
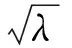
下述定理给出了Vφ的奇异值刻画：

证由φ为内函数且φ(0)=0， 根据引理2可知Cφ为等距算子， 即有

这样我们可以得到

又因为

所以

从而可以得到V*1=0.

同理， 由于

所以有

从而

于是

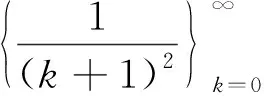
例1设φ=zN， 其中N为大于1的正整数， 则σ(Vφ)={0}.

证假设λ≠0是Vφ的特征值， 那么存在非零函数f∈H2， 使得

Vφf=λf

根据定义知

则有

(4)

首先， 比较(4)式两端的常数项， 可得