一种基于改进贝尔曼方程的最短路径规划算法

鲁 韵 王 姣

(武昌首义学院机械与自动化学院 武汉 430074)

0 引 言

无人驾驶技术的快速发展给城市交通带来了一定压力.随着交通网络的规模越来越大，其路径规划也越来越复杂.最短路径规划作为提高无人驾驶车辆通行效率、缓解城市交通压力的基本方法已成为研究热点.

郭兴海等[1]采用多目标与速度控制的方法提出了一种全局路径规划方法，该方法对静态全局路径规划的效率提升明显.赵卫东等[2]通过添加约束的方法提出了一种两阶段搜索的A～*全局路径规划算法，相比于传统算法，该算法改进了动态全局路径规划计算问题的效率.然而，全局路径规划考虑了地图上所有的节点信息，通常非常耗时，因此提出最短全局路径算法，如Voronoi图方法[3]，单元分解法[4]和随机规划法[5]等.尽管这类算法执行速度很快，但对于如何生成足够的样本以覆盖和连接配置空间，以及如何优化生成路径等问题并未得到很好解决.在路径规划问题中效率和可达性的平衡一般要根据项目的实际情况进行取舍，这给工程实际带来了一定的困难.

本文提出一种最短路径规划算法，该算法将目标集看作有限维的欧几里德空间并采用改进贝尔曼方程选择当前最佳的适宜型控制策略以解决其效率和精度问题.

1 最短路径问题的数学描述

假设一个具有有限集合节点的图为X∪{t}，一组有限的有向弧为A⊂{(x,y)|x,y∈X∪{t}}，其中t为目标节点.在每个x∈X节点处，可以从非空集合U(X)中选择一个控制或动作u，它是有限集合U的子集.然后，从非空集Y(x,u)⊂X∪{t}中选择一个后续节点y.那么对于所有的y∈Y(x,u)都有(x,y)∈A，此过程中的成本函数记为g(x,u,y).目标节点t具有可吸收性并且生成过程中不产生成本.所以从这个意义上说，目标节点t的唯一输出弧是(t，t)且对所有的u∈U(t)都有g(t,u,t)=0.

为每个节点x∈X分配一个控制μ(X)∈U(x)，其中μ(X)为控制策略函，用M表示所有控制策略的有限集.在控制策略μ下从节点x0∈X开始的一条可能的规划路径可视为弧序列p：

p={(x0,x1),(x1,x2),…,}

(1)

对所有的k≥0都有xk+1∈Y(xk,μ(xk)).P(x0,μ)为从x0开始的控制策略μ下的所有可能路径的集合.路径p∈P(x0,μ)的长度为

(2)

若式(2)中的级数收敛，则有

(3)

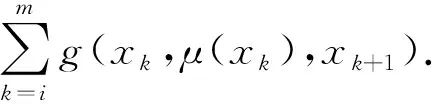
当x0≠t时，对给定的控制策略μ，若路径p∈P(x0,μ)见式(4)，则称其为路径终止.

p={(x0,x1),(x1,x2),…,(xm,t),(t,t),…}

(4)

式中：m为定义范围内的一个正整数，x0,…,xm为不同的非目的节点.因为对所有u∈U(t)都有g(t,u,t)=0，控制策略μ下具有式(4)形式的终止路径p的长度为

Lμ(p)=g(xm,μ(xm),t)+

(5)

有限弧子集描述了控制策略μ的一个重要特征信息：

Aμ=∪x∈X{(x,y)|y∈Y(x,μ(x))}

(6)

因此，在某种意义上Aμ与自弧(t,t)共同构成一组唯一路径∪x∈XP(x,μ).若对每个x∈X都在P(x,μ)中存在一个终止路径，则称Aμ为目的地可连接型.如果弧Aμ的子图是非循环的(即不包含循环)，则称Aμ为适宜型.因此，到目的节点时当且仅当∪x∈XP(x,μ)中所有路径都是简单路径，则称μ为适宜型.等价于当且仅当Aμ为目的地可连接型并且不存在循环时，μ为适宜型.“适宜型”策略的定义与随机最短路径问题中的定义一致，表示以概率1到达目的地的策略[6-8].如果μ为不适宜型，则称寻求路径的整个过程为不适宜过程，在这种情况下，弧Aμ的子图会至少包含一个循环，见图1.

对于适宜型的控制策略μ，对每个x∈X从x开始的有限可能路径集合上最坏情况的路径长度为

(7)

式中：Jμ(x)为弧Aμ的非循环子图中从x到t的最长路径的长度.由于此非循环图中有有限多条路径，因此，在简单情况下可以通过枚举并比较这些路径长度的方法来找到Jμ(x).因此对于所有的x∈X，在经典最短路径问题的假设下，需要找到一个适宜型的最佳控制策略μ使Jμ(x)最小.将此称为鲁棒最短路径选择问题(RSP)，且RSP中的极小化只建立在适宜型的控制策略之上[9-11].

2 基于改进贝尔曼方程的极值算法

2.1 研究假设

研究假设如下：①对每个有向图集，至少存在一个适宜型的控制策略；②对于每个不适宜型的控制策略μ，弧Aμ子图中的所有循环的长度都为正.

该假设与经典的确定性最短路径问题中的假设一致，即Y(x,μ)由单个节点组成.假设①等价于假设每个节点都有一个路径连接到目的地；假设(2)等价于假设图中的所有有向循环的长度均为正.对假设②进一步补充为假设图中的所有有向循环的长度均为非负数.该假设适用于所有弧长g(x,u,y)均为非负的情况，此情况下保留了存在零长度循环的可能性.

2.2 改进贝尔曼方程的极值算法

将函数Jμ(x)的定义扩展到不适宜型的情况中去.对于适宜型控制策略μ，Jμ(x)可由式(7)计算，对路径p∈P(x,μ)，最长路径的长度为

定义：

(8)

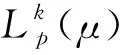
(9)

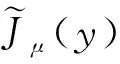
(10)

通过式(9)～(10)，对于一个适宜型的控制策略μ，任何最短路径算法均可用于解决该最长路径问题.对不适宜型的μ，Jμ(x)→∞, 相应的解决最长路径问题的算法也就不再适用.此时，需要寻求一种最小化算法找到目标函数式(11)的最小值，使之同时适用于所有的x∈X.这与第一节中鲁棒最短路径选择问题不同，该最小化算法要对所有的控制策略成立.

(11)

将式(11)所描述的极值问题抽象化，改写为匹配贝尔曼方程式(8)～(9)的形式，从而将其转化为抽象动态规划问题.用E(X)表示函数集J:X→[-∞,∞]；用R(X)表示函数集J:X→(-∞,∞).注意，因为X是有限集，所以R(X)可以看作有限维的欧几里德空间.引入映射H:X×U×E(X)→[-∞,∞]，为

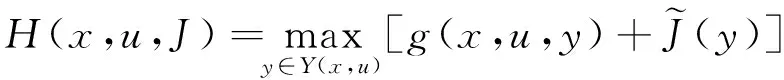
(12)

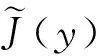
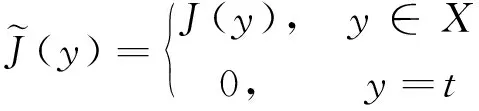
(13)

对任意的控制策略μ，定义映射Tμ:E(X)→E(X)为

(TμJ)(x)=H(x,μ(x),J),x∈X

(14)

注意到不动点方程Jμ=TμJμ与贝尔曼方程(8)相同，映射Tμ:E(X)→E(X)可写为

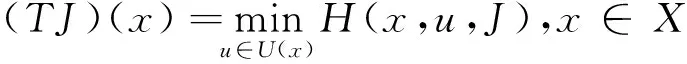
(15)

等价于

(16)

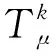
引入一个零函数：

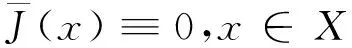
(17)

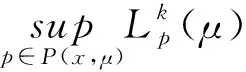
(18)

将上式带入式(8)，可得到：

(19)

这样就所得到了在2.1的假设下经典确定性最短路径问题的主要分析结果，即改进贝尔曼方程的极值算法，该算法可以抽象形式表述如下：

1)J*为T在R(X)内的唯一不动点，对所有的J∈R(X)，Tk(J)可以将转换为J*.

2) 对最短路径规划问题，存在一个最佳的适宜型控制策略，并且只有在该适宜型控制策略下才能得到最优解.

3) 当J=J*时，当且仅当对式(16)中所有的x∈X它都能取得最小值，那么控制策略μ即为最优.

3 试验结果与分析

3.1 标准最短路径规划仿真结果与分析

通过仿真模拟比较改进贝尔曼方程的极值算法和快速行进算法在四个不同种类地图上的最短路径寻迹结果，见图1～4.

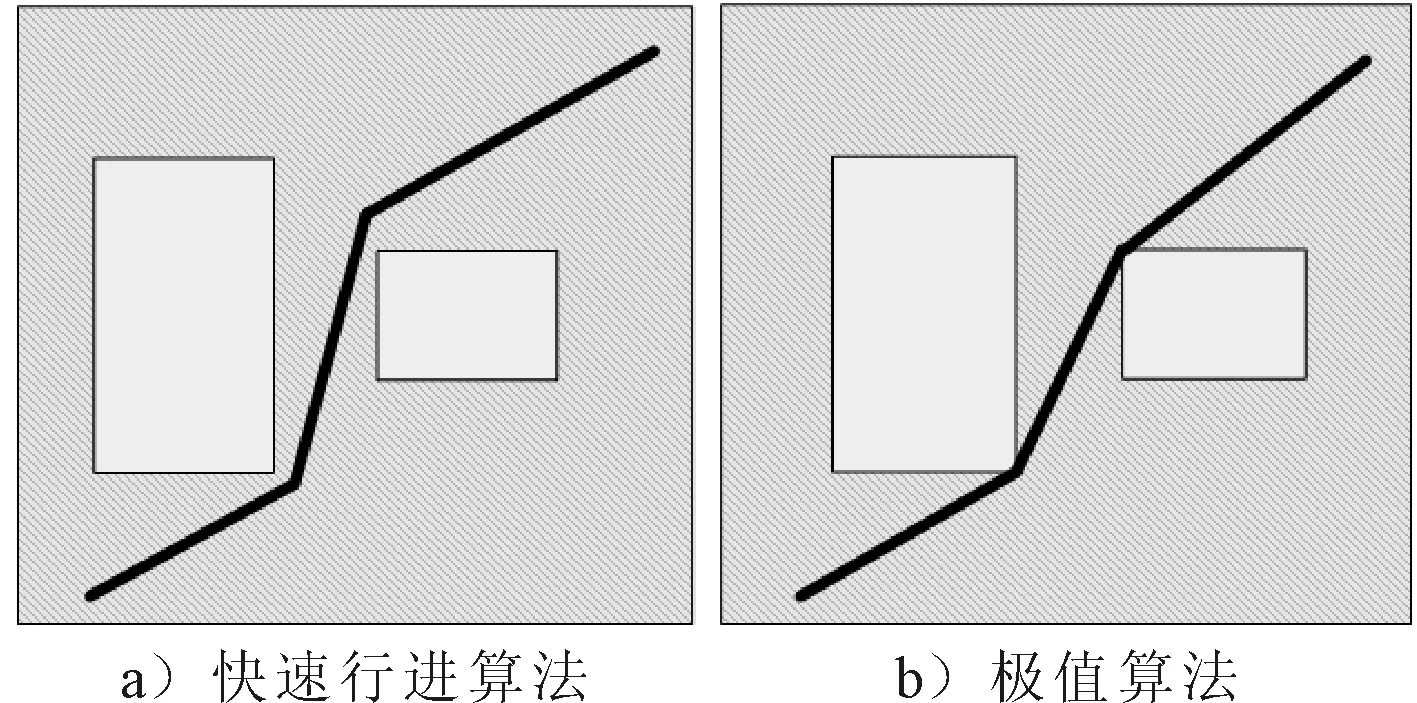
图1 快速行进算法与极值算法在地图1的最短路径规划仿真结果对比

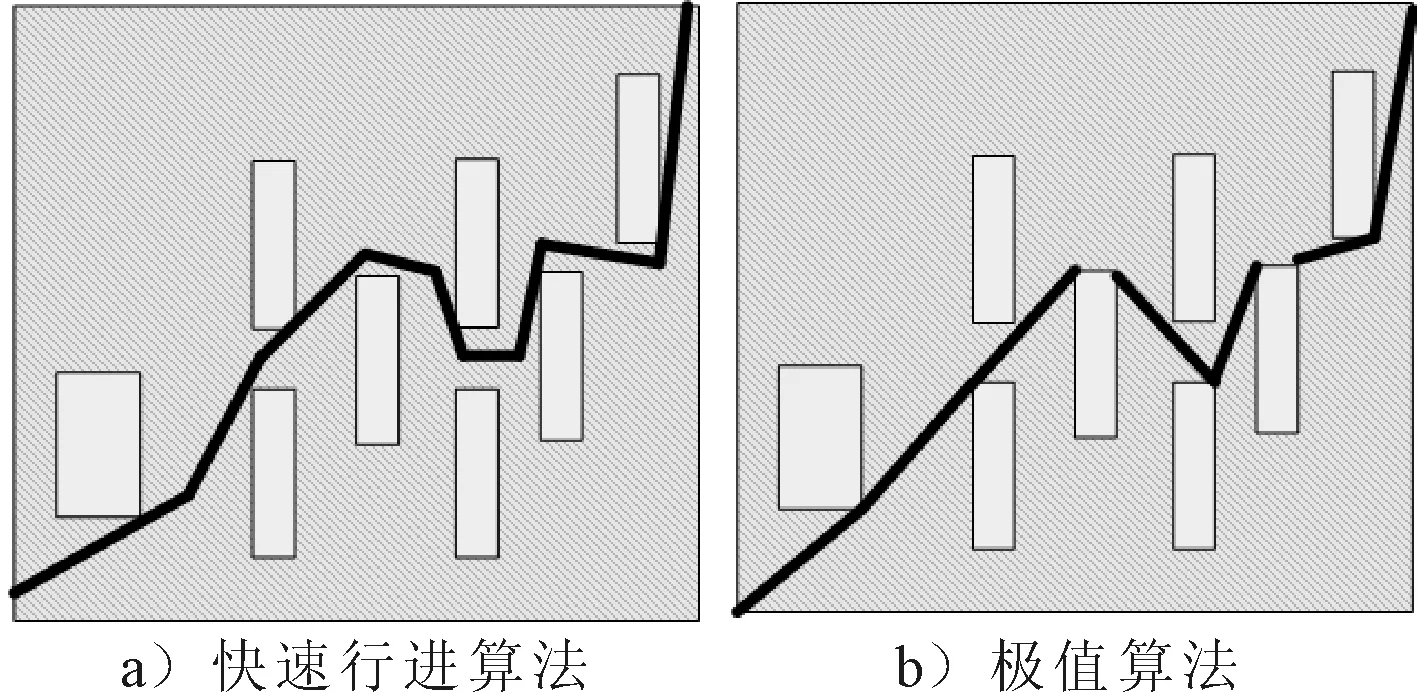
图2 快速行进算法与极值算法在地图2的最短路径规划仿真结果对比

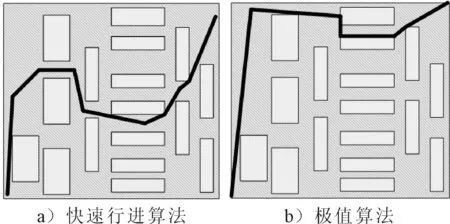
图3 快速行进算法与极值算法在地图3的最短路径规划仿真结果对比

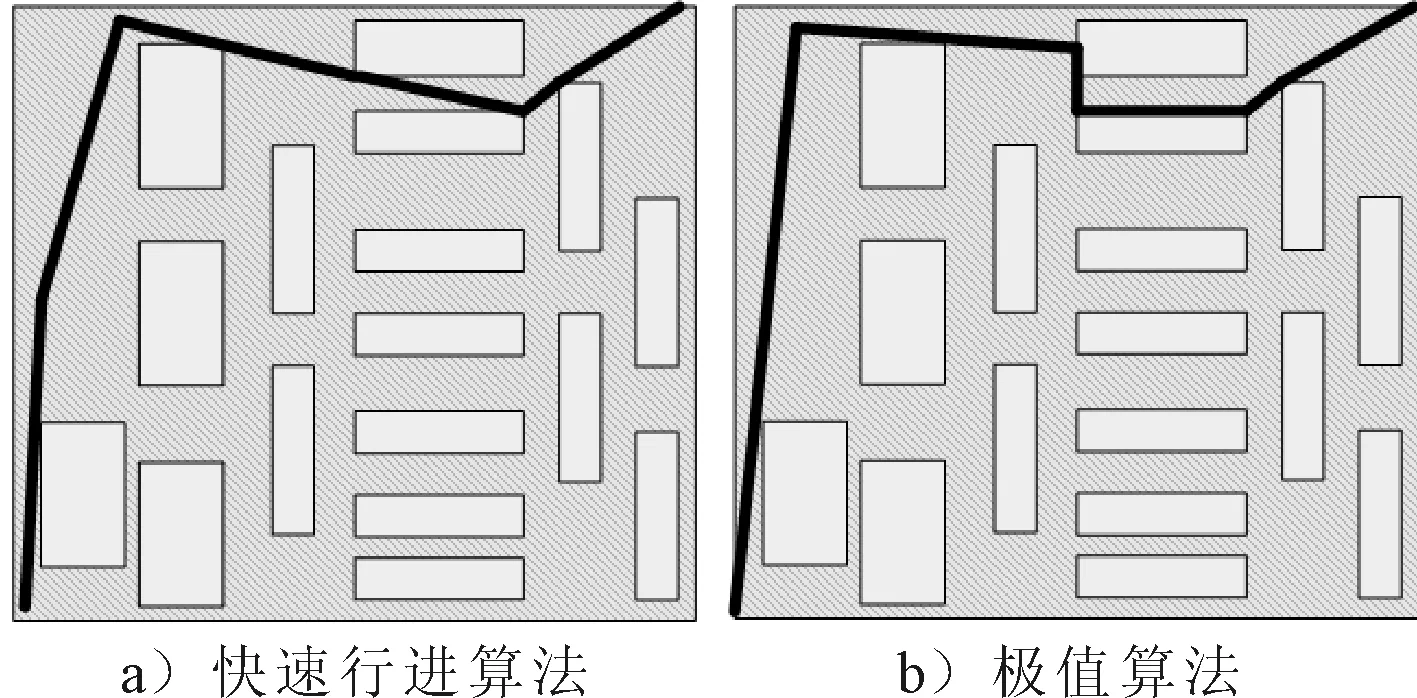
图4 快速行进算法与极值算法在地图4的最短路径规划仿真结果对比

由仿真结果可知，改进贝尔曼方程的极值算法生成的路径比快速行进算法生成的路径更精确，尤其是在垂直和水平方向.这是因为快速行进算法中所使用的2阶龙格-库塔法的累计误差影响了原始常微分方程在路径恢复中的数据精度.此外，极值算法所仿真出的最短路径的起始位置和终点位置非常精确，但快速行进算法只在特定范围内比较准确.然而，如果缺少适当的线性插值误差校正，极值算法路径的某些中间段部分会变得比快速行进算法路径稍差.导致这种结果的原因在于路径上的一个附加有限弧节点可能被错误地分配给另一个有限弧节点的父有限弧节点.

表1为当最大成本值较大时，极值算法和快速行进算法的计算时间.通过仿真分析，因此当最大成本值设置为较大数值时，极值算法的总时间比快速行进算法快.极值算法的计算速度是稳定的，其计算速度仅取决于图大小的比例，计算复杂度仅取决于有限弧节点的个数.极值算法对最大成本值没有影响，因此其总时间几乎等于有限弧节点的前向传播时间.虽然快速行进也具有稳定的传播速度，但其路径计算时间将取决于环境的复杂性，其收敛速度也受最大成本值的影响.

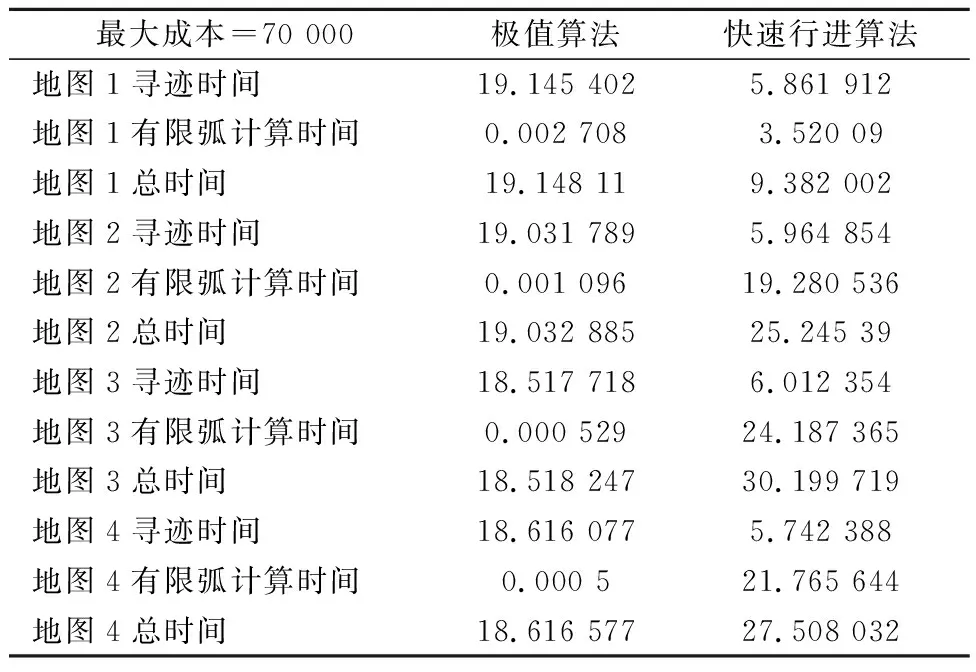
表1 极值算法和快速行进算法的计算时间比较 单位：s

3.2 涉及追踪的动态路径规划仿真结果与分析

通过应用极值算法和路径恢复规则，对涉及追踪规避问题的动态路径规划进行了仿真.地图尺寸也为100×100网格，蓝色标记的路径为追踪者，绿色标记的路径为躲避者，二者的速度均设置为1单位/s.躲避者的行动模式设置为试图逃离追踪者的追捕，结果见图5.在第12 s，因为躲避者稍微向上移动，可以看到新规划路径在公共有限弧节点重置后被立即更新，说明极值算法具有较好的动态性能.从最后追捕结果可以得到如果躲避者的躲避路径总使得障碍物出现在躲避者和追赶者之间，则当躲避着和追踪者速度相同时该方法不能保证捕获成功.然而，如果追踪者的速度更快，由于极值算法在每个时隙都提供了最短的追踪路径，所以无论躲避者如何移动，该方法都能保证成功.

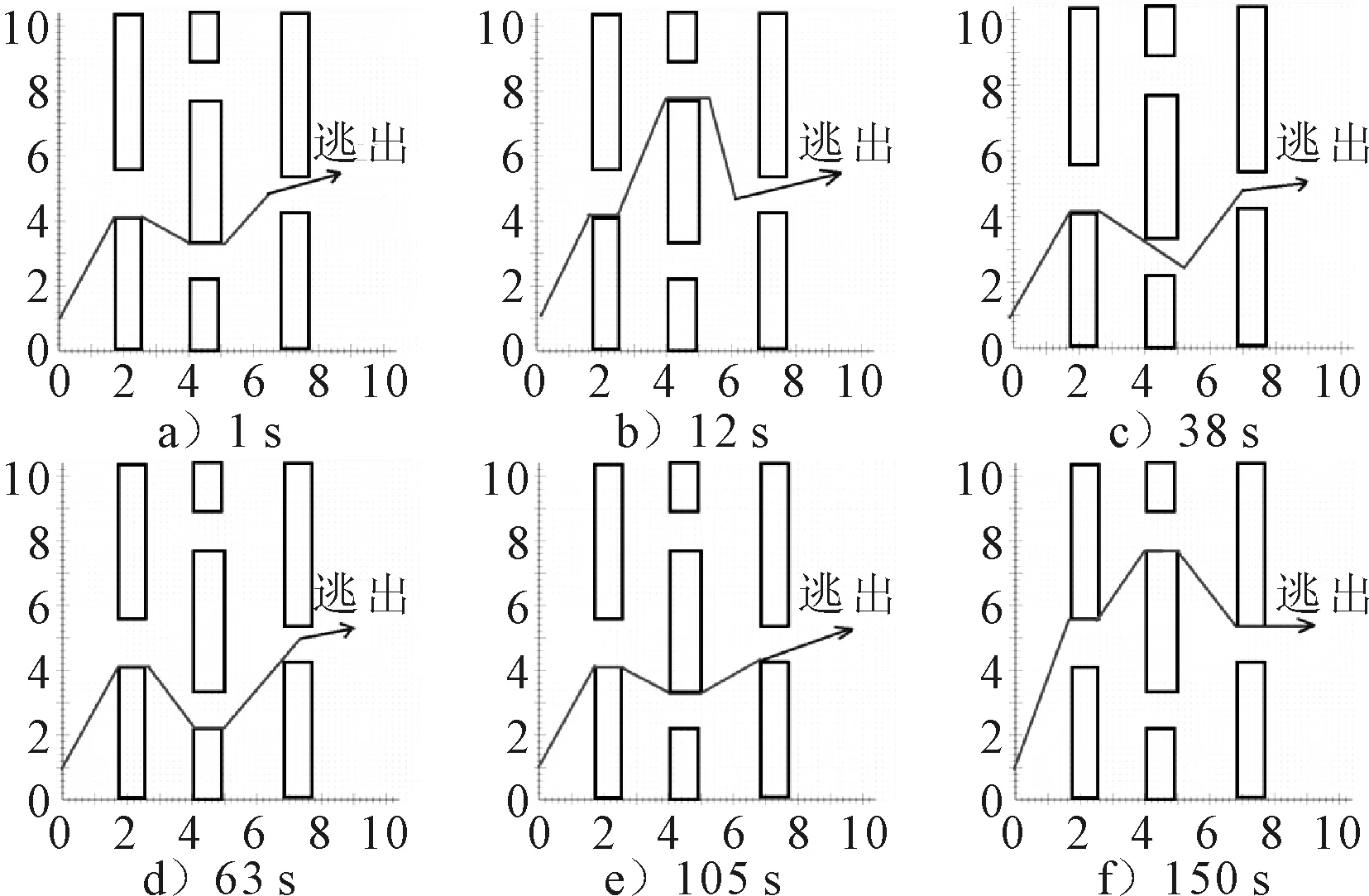
图5 涉及追踪的动态路径规划仿真结果

4 结 束 语

考虑到无人驾驶车辆的安全性和城市交通通行效率，其静态和动态路径规划需要兼顾准确性、可靠性和快速性.文中提出了一种基于改进贝尔曼方程最短路径规划算法，该算法可以选择当前最佳的适宜型控制策略以解决其效率和精度的平衡问题.仿真实验结果表明，极值算法生成的路径比快速行进算法生成的路径更精确，尤其是在垂直和水平方向.极值算法的计算速度是稳定的，其计算速度仅取决于图大小的比例，计算复杂度仅取决于有限弧节点的个数，其动态路径规划性能优于快速行进算法.但该方法在任务分配复杂的情况下，其协同能力仍有提升空间，有待后续进一步研究.