融合模体图神经网络和自编码器的链路预测

鲁富荣，原之安，钱宇华+

1.山西大学大数据科学与产业研究院，太原030006

2.山西大学计算智能与中文信息处理教育部重点实验室，太原030006

3.山西大学计算机与信息技术学院，太原030006

网络是对现实世界对象及其相互作用关系的抽象表示，其中节点代表实体对象，链接表示实体间的成对关系。如生物蛋白质相互作用网络、科学研究中的引文合作网络以及社交网路中朋友关系网络。这些网络中包含丰富的节点属性信息、结构信息以及网络演化信息。在网络的演化过程中，某些链接可能出现或消失，需要对缺失数据进行补全以及对未来可能出现或消失的链接做出预测。同时作为数据挖掘领域的一个重要分支，链路预测具有很重要的现实意义。例如，生物网络分析[1]中，链路预测可以对生物数据进行挖掘和补全。科学合作者[2]及朋友推荐[3]中，链路预测可以推荐相关的新的朋友和科研合作者。

链路预测问题作为数据挖掘领域的经典问题，已有很多相关的模型和方法。目前链路预测的方法大多基于节点表示的相似性假设，也即节点对的表示越相似，则产生链接的可能性越大，因此问题就归结为寻找高质量的节点表示，使得节点的表示保留原网络的拓扑特征，也即原网络有边相连的节点，在节点的表示中较为相似。

近年来，由于图结构的网络嵌入方法和图神经网络的迅速发展，进一步提升了模型对网络节点的表示能力。然而大部分模型都利用节点的直接邻居的信息进行卷积操作，并未充分利用网络的结构信息且较少考虑网络的高阶拓扑信息。

为提高节点的表示能力且兼顾计算效率，本文提出了基于模体的图神经网络链路预测模型，主要贡献包括三方面：

（1）在自编码器框架下，提出一种模体图神经网络模型为编码器的链路预测模型，该模型提取了网络的高阶拓扑特征。

（2）构建了基于同质网络的模体图神经网络模型，根据指定的模体结构构建节点的邻域，进而聚合邻居信息得到节点的表示。

（3）不同数据集上的实验结果表明本文的模型有效提高了链路预测的准确率。

1 相关工作

传统的链路预测方法主要分为两大部分：基于拓扑指标的方法和基于机器学习的方法。第一类方法又可分为基于局部拓扑的方法和基于全局拓扑的方法。此类方法通常假设节点间的共同邻居越多则越相似。如共同邻居CN（common neighbour）[4]和AA（adamic-adar）[5]指标以及基于资源分配的RA（resource allocation）[6]指标等，这类方法的优点是计算效率高且可并行，但缺点是准确率相对较低，尤其当网络比较大而且稀疏时。基于全局的方法利用全局的拓扑信息来计算节点间的相似性，准确度有一定的提升，但由于利用了全局的拓扑信息，计算复杂度偏高。另一大类方法是基于机器学习的模型，包括基于机器学习的分类方法、基于概率似然函数的方法和矩阵分解方法，其中分类方法将节点对标记为0 或1，0表示不存在链接，1 代表存在链接，进而将链路预测转化为二分类问题。该类方法用的是监督学习中一些常用的分类算法（如决策树、K 近邻法、支持向量机）对缺失的连边进行预测。基于概率的模型主要包括层次结构模型，这类方法假设网络有一定的先验的分层结构或分块的结构[7]，给出了网络的结构特征的定量刻画。基于矩阵分解的方法将链路预测视为邻接矩阵的填充问题，基于非负矩阵或者谱分解等方法，给出节点的向量表示，进而计算节点的相似性，预测节点间链接的存在性。这类方法的学习参数较少，但计算复杂度较高。

随着深度学习的深入发展以及深度学习和网络数据挖掘的融合，进一步提高了模型的表达能力，国内外学者提出了一系列基于图嵌入和图神经网络的链路预测方法。网络嵌入的方法是自动从原始网络结构信息中抽取局部的和全局的特征，将网络节点映射到低维的向量空间。这类方法包括DeepWalk[8]、node2vec[9]、LINE[10]以及struc2vec[11]。相比传统方法，这类方法达到了较高的链路预测准确率。然而这类方法也存在一定的局限性：首先，训练过程中缺乏监督信息，使得节点的表示与任务的关联性不足。其次，在运算过程中要多次用到基于全局拓扑结构的随机游走方法，因此计算复杂度较高。

由于深度学习在图像分类和自然语言处理方向的成功应用，推动了深度学习方法在图网络方向的迁移。借鉴卷积神经网络的思想，图卷积网络（graph convolutional networks，GCN）[12]结合网络的全局拓扑信息和节点的属性信息，对节点的邻居信息进行聚合，最终基于节点分类任务给出了节点的表示。在此基础上，Velickovic 等提出了图注意力网络（graph attention network，GAT）[13]，基于网络的节点一阶邻居信息和属性信息，将任意两个节点的信息进行拼接作为连边信息，得到节点j相对于节点i的注意力权重，进而按邻居节点的注意力权重不同，对邻居信息进行加权聚合，得到节点的最终表示。图神经网络模型得到了更好的节点表示，进而达到更高的节点分类和链路预测准确度。同时也存在如下缺陷：（1）聚合函数采用最大或平均的方法，不能很好地对网络进行区分。（2）在网络增长或遭受攻击时，网络结构会发生改变，此时要得到节点表示，只能重新用GCN展开计算。（3）在网络表示的过程中用到了节点邻居信息，但并未用到网络的高阶信息，也即GCN 对网络的拓扑信息利用不充分。

对于第一个问题，Graph Isomorphism Network[14]进行了初步的尝试，聚合过程采用MLP+sumpooling，在多个任务上准确率达到目前最好的结果。在第二个问题上，图神经网络模型GraphSage[15]在迭代过程中固定采样尺寸，然后采取一种特殊的聚合策略，对不断增长的网络的表示提供了很好的解决方案。对于第三个问题，Zhang 等人[16]提出了SEAL（learning from subgraphs，embeddings and attributes for link prediction）模型，该模型从原网络中提取包含待预测节点对的特定子图结构，得出一系列拓扑指标作为节点对的向量表示，进而学习出两个节点存在链接的可能性。然而利用子图结构进行学习时，对于每一对待预测节点u、v，需要构建以u、v为中心的子图，同时计算该子图对应的拓扑指标，进而利用神经网络进行相应的训练，计算成本较高。由于网络由一些基本的子图结构（motif）构成，有很多研究者试图将图神经网络和模体信息结合起来执行下游的任务。

Wang 等人[17]提出了基于motif 的深度特征学习模型，利用正则表达式和图自编码器模型保留网络的模体特征，最后获得节点的表示。该模型仅利用了三阶模体的信息而且并未真正将模体信息和图神经网络进行融合。Sankar 在2019 年给出了基于异质网络模体结构的图神经网络模型Meta-GNN[18]，将异质模体结构嵌入图卷积网络，并结合图注意力模型，对异质网络的节点进行了分类。然而对于同质网络，该模型并没有给出相应将高阶结构和图神经网络相结合的解决方案。

本文提出的基于模体图神经网络的链路预测方法，将网络的模体结构和图神经网络模型结合，融合了网络的高阶拓扑特征，增强了图神经网络的表示能力。在复杂网络的链路预测验证了模型的有效性，可运用到后续其他任务中。

2 预备知识

2.1 基本定义

本节列举了文章中的预备性知识和记号，如表1所示。设G=(V;E)表示一个图网络，V表示节点集，E表示边集，若两个节点vi、vj有边相连，则(vi,vj)∈E。模体M是指由网络的少量节点构成的图G的子图，定义如下：

表1 文中使用的符号和变量Table 1 Variables and notations in text

定义1（模体）[18]设M是图G=(V;E) 的连通子图，且满足对任意(vi,vj)∈EM,(vi,vj)∈E，则称M为G的模体，其中EM表示子图M的边集。

不同三阶模体和四阶模体如图1 所示（表示为M3.、M4.，每个模体Mij的第一个下标i代表节点数，第二个下标j是指定排序），在科研合作网中模体M31代表两个作者和另外一位都有合作，但他们彼此并没有合作。往往这种情况发生在普通科研人员和科研名人的合作中。M32代表的则是接近同类一水平的科研人员的合作，三位作者彼此之间都有合作。

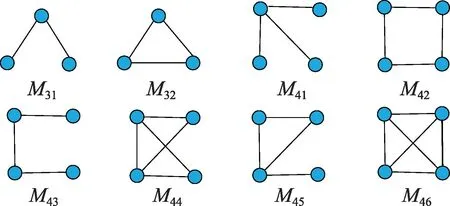
图1 所有的三模体和四模体Fig.1 All tri-motifs and quad-motifs

定义2（模体的实例）[18]设Su=(VS，ES)是模体S的包含节点u实例，如果Su是图G的一个子图，且有VS∈V,ES∈E，使得对任意的x,y∈VS,(x,y)∈ES存在一个双射ψ：S→M满足 (x,y)∈ES当且仅当(ψS(x),ψS(y))∈EM。

定义3(模体邻居）对于指定的模体类型M，节点vi的一阶邻居中，与vi位于同一类型模体中的节点称为节点vi基于模体M的邻居。

图2 中的两个模体(v,v1,v2)以及(v,v3,v4)是模体M32的两个实例，同时v1、v2、v3、v4也是v的模体邻居。在不同的网络中，有隶属于网络的不同特征模体，其发生频率远大于随机图中该子图的发生频率。在计算过程中，为提取网络的模体特征，需要从网络中搜索与不同类型模体同构的所有模体，该过程计算成本较高。为降低计算的复杂度，本文仅考虑三阶和四阶模体，首先利用软件mfinder[19]对网络所包含的不同类型模体比例进行计算，给出每个网络的模体分布情况。

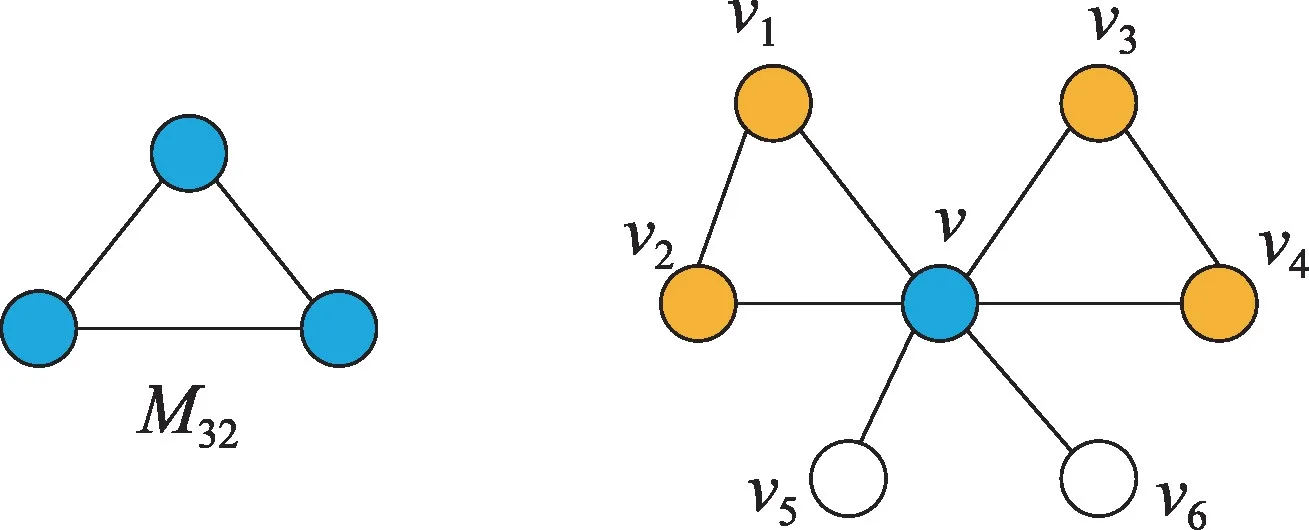
图2 节点v的接受域包含v1、v2、v3、v4Fig.2 Receptive field around node v contains v1,v2,v3,v4

2.2 图卷积网络

传统的图卷积网络模型结合了网络的拓扑信息和属性信息，在网络的每一层中将节点的邻居信息进行聚合，然后进行非线性变换得到节点的表示，具体的形式如下：

输入是网络的邻接矩阵A∈RN×N和节点的属性矩阵X∈RN×D，V是图G的节点集，N是网络的节点数，是邻接矩阵A对应的标准化拉普拉斯矩阵，WD×F是对应的权重矩阵，σ表示激活函数（这里指Softmax），H是一次迭代的输出，即原网络节点的低维表示。在神经网络的一次迭代过程中，节点vi的表示聚合了其一阶邻居的信息，最后通过激活函数得到节点的低维表示，对于每个节点，上述过程可表示为：

一个节点v的接受域是节点的一阶邻居构成的邻域。在本文中一个节点v的接受域是指和v包含在同一类型模体中的节点，如图2 所示。类似于邻接矩阵，这里也定义了同质网络的模体邻接矩阵。

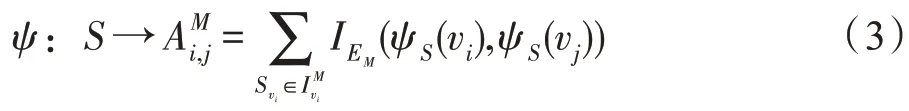
式（3）是模体S到AM的一个映射，AM是一个矩阵。IS(u)是一个示性函数，如果u∈S,则IS(u)=1,否则为0。定义对角矩阵DM∈RN×N，对角线上的第i元素是包含第i个节点的模体M的个数，也即。通常对于一个给定的机器学习任务，需要综合考虑多个相关的模体结构，一类模体代表一种结构特征，然而对给定的数据挖掘任务通常需要多个方面的特征，本文采用多类模体的信息构建神经网络。

3 基于模体图神经网络的链路预测模型

3.1 模体图神经网络

本文引入一个基于模体的空间卷积操作来提取节点的特征[18]。给定模体M以及目标节点vi，设输入节点的是1 维向量，经过映射之后的节点的维度F=1。定义节点vi权重矩阵w0及其邻居节点vj的权重wj，则节点v处的卷积可定义为与节点vi基于模体M的模体邻居的加权和，即：

其中，xi、xj表示节点vi、vj的属性向量。hM(vi)表示节点vi的卷积输出，σ(·)表示激活函数，例如ReLU(·)或Softmax(·)，权重共享过程就是赋予节点vi的模体邻居相同的权重。进而可将上式的情况推广到一般情形：节点的属性矩阵X为N×D维的矩阵，输出维度为F，则有：

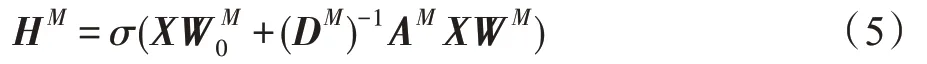
其中，WM是权重矩阵，HM是在模体M下的卷积输出。由于在表示每个节点的过程中，单类模体的特征信息不能充分地表示节点，有必要综合多类模体的信息。但在聚合的过程中不同类型的模体对每个节点的重要性各不相同，为了体现卷积过程中各类模体对节点表示的不同影响，本文加入模体的注意力机制[18]。

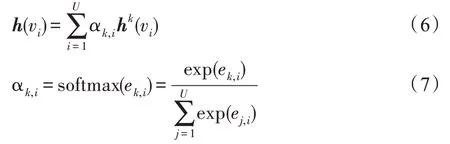
式中，U是模体的个数，ek,i=α(hk(vi))=W·hk(vi)是关于hk(vi)的一维卷积，注意力系数αk,i反映了模体Mk对于节点vi的重要性，hk(vi)是节点vi在Mk下的卷积输出。本文将模体图神经网络模型简称为MGNN（motif-based graph neural network），其网络架构如图3 所示。经过对不同类模体的卷积的聚合，在激活层连接注意力网络，这两部分构成一个基本神经网络单元，进而逐层迭代。最后对卷积层聚合各类模体的卷积输出之后，通过全连接网络得到最终节点的表示。

图3 MGNN 的深度图神经网络框架Fig.3 Deep graph neural network framework MGNN

3.2 图自编码器

本文的模型采用了自编码器VGAE（variational graph auto-encoders）[20]结构，自编码器是通过编码器和解码器结构对节点进行表示的一种无监督学习方式，以网络邻接矩阵A和属性矩阵X作为输入，编码器采用的是模体图神经网络模型（MGNN），对编码以后的向量做内积运算作为解码器，给出连边的预测值，最后选取交叉熵作为损失函数进行梯度反传（结构如图4 所示）。本文的算法流程如下：

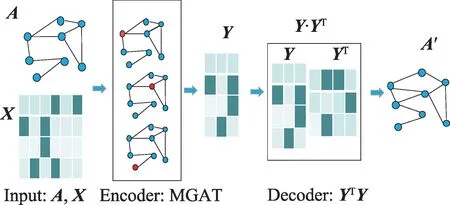
图4 图自编码器的结构框架Fig.4 Architecture of GAE

算法1结合图自编码器的模体图卷积网络模型

3.3 复杂度分析

4 实验与结果

本文提出了基于同质网络的MGNN 的链路预测模型，并且在几个实际网络数据集验证了方法的有效性。训练过程中，数据集的部分链接（正类边）已被删除，而所有节点特征保持不变。用移除的边和相同数量的随机抽样的未连接节点对（负类边）形成验证集和测试集。根据模型正确区分正类边和负类边的能力来比较模型。验证集和测试集分别包含5%和10%的引文链接，剩余作为训练集。验证集用于优化超参数。用glorot 方法初始化神经网络权重，学习率为0.001，神经网络的层数为3 层，一次实验训练200轮，每个数据集训练20次，计算平均值和方差。

4.1 度量标准

本文使用的链路预测的度量指标为AUC（area under the curve of ROC）和AP（average precision）。AUC 是ROC 曲线下方的面积，AP 是平均准确率。AUC 值至少大于0.5，AUC 的值越高，算法的精确度越高，但AUC 的值最高不超过1。AP 是在不同召回率下准确率的加权平均，取值越高表明算法精度越高，同样不超过1。

4.2 数据集

本文将在Cora、CiteSeer、PubMed 3 个数据集上测试提出的方法。下面从数据集大小和数据特点等方面分别介绍这3 个数据集。

Cora 数据集共2 708 个样本点，每个样本点都是一篇科学论文，每篇论文都由一个1 433 维的词向量表示。

CiteSeer 数据集是从CiteSeer 数字论文图书馆中选取的一部分论文，整个语料库共有3 327 篇论文，在词干提取和删除停止词之后，只剩下3 703个单词。

PubMed 数据集包括来自PubMed 数据库的19 717 篇关于糖尿病的科学出版物。引文网络由44 338 个链接组成。数据集中的每个出版物都由一个由500 个唯一单词组成的字典中的TF/IDF 加权词向量来描述。

用mfinder 软件给出每个网络的模体分布情况（如表2 所示）。为进一步提高计算效率，选取网络中包含3 个节点和4 个节点的模体。

表2 3 个数据集各类模体的比例Table 2 Proportion of various motifs in 3 datasets 单位：%

4.3 结果

本节选取几个算法进行对比实验，分别是MGNN、VGAE[2]、node2vec[9]、LINE[10]、DeepWalk[8]、DeepLinker[22]，MGNN 表示本文结合自编码器的方法，VMGNN 表示本文方法与变分自编码器结合的方法，(*)表示网络输入仅考虑拓扑信息而不包含属性信息。Deep-Walk、LINE、node2vec 是基于拓扑结构的网络嵌入的方法，结合随机游走和Skip-gram 的思想给出节点的表示。VGAE 是结合图卷积网络和自编码器的模型，在链路预测上取得了较好的效果。DeepLinker 是基于图注意力网络的链路预测模型，在链路预测上取得了较好的表现。在此情况下，网络的输入矩阵包括邻接矩阵和维度为节点数的单位矩阵，实验过程中主要选取模体M31、M32、M42构建模型。

4.4 实验描述和总结

实验结果如表3 所示，在两个数据集上结合高阶结构信息之后本文方法在大部分网络上能够得到网络节点的更好的表示，链路预测的结果较传统方法提升了1%～4%。同时在PubMed 数据集上的预测结果略低于VGAE，由于考虑了节点的模体结构信息，模体的数目未必服从正态分布，因此自编码器在某些情况下的实验结果会低于变分自编码器对应的结果。

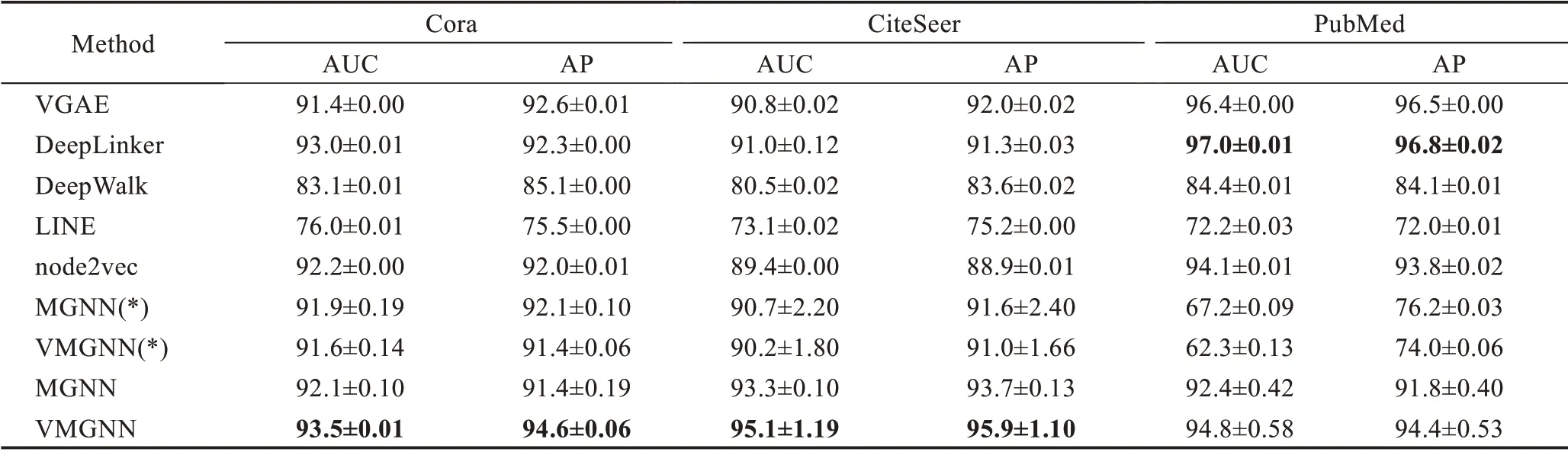
表3 基于MGNN 的链路预测实验结果Table 3 Experimental results of link prediction modes based on MGNN 单位：%

4.5 消融实验

本节将本文方法和VGAE 以及MGNN+MLP（全连接网络）进行了对比，VGAE 将图卷积网络GCN 和自编码器相结合，在链路预测任务中取得了很好的效果。MGNN+MLP 是在MGNN 网络之后链接了全连接网络MLP，以说明本文的模型MGNN+Attention的有效性。结果如图5 所示。

图5 MGNN+Attention、MGNN+MLP、VGAE对比实验Fig.5 Comparison of results on MGNN+Attention,MGNN+MLP and VGAE

实验结果表明，本文模型在大部分情形下优于其他两类模型，进一步说明模型中融入模体结构可有效提高神经网络的预测能力。同时MGNN+MLP与MGNN+Attention 的对比，也验证了MGNN 网络中链接注意力网络的有效性，说明在节点表示的过程中，需要考虑不同模体的重要性。

4.6 实验效率对比

本节给出了各个模型在网络Cora 和CiteSeer 上链路预测任务的运行时间对比，本文采用的实验环境是Ubuntu 16.04，CPU 为Intel®Xeon CPU E5-2620 v2@2.10 GHz，内存容量48 GB，图6 给出了6 个相应算法的运行效率对比图。

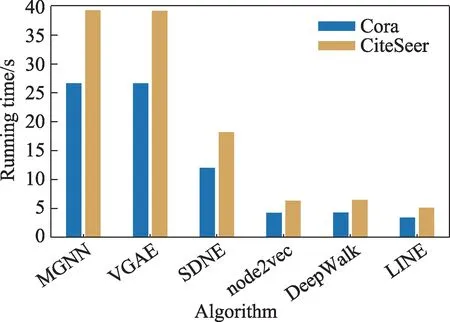
图6 在Cora 和CiteSeer两个数据集上算法效率对比Fig.6 Efficiency comparison of algorithms on Cora and CiteSeer datasets

如图6 所示，基于图表示学习的浅层网络模型运行效率较高，但此类模型很难学习到网络中节点的复杂结构信息。本文方法结合了多层的神经网络结构以及高阶的模体信息，尽管计算成本较高，但在链路预测的指标上较图表示学习的方法取得了较大幅度提升。同时由于模型采用了自编码器框架，运行时间与图自编码器（VGAE）等模型的运行时间接近。

5 结束语

本文提出了一种基于同质网络的模体图神经网络链路预测模型，在图卷积网络的基础上结合了网络的高阶结构-模体的信息，结合每一种模体结构给出了节点的表示，并进一步考虑了各类模体对于节点的注意力权重，最后利用节点的表示重构网络。在几个常规的引文数据集的链路预测任务上验证了算法的有效性。在大规模的网络中计算效率和准确度有待进一步改善。

在模型的训练过程中，MGNN 用到了节点的高阶模体信息，模型的计算成本有一定的增加，后续的研究考虑采取适当的采样方法来降低模型的复杂度。