面向算法选择的元学习研究综述
2023-01-17李庚松李红梅郑奇斌宋明武任小广
李庚松,刘 艺+,秦 伟,李红梅,郑奇斌,宋明武,任小广
1.国防科技创新研究院,北京100071
2.军事科学院,北京100091
3.天津(滨海)人工智能创新中心,天津300457
人工智能是数据处理与分析的重要技术,为人们利用数据进行决策和研究提供了有力支撑。在人工智能的不同领域中,研究人员提出了大量算法,然而,不同算法在有限数量的问题上具备优越性能,不存在一个适用于所有问题的可行算法,该现象被称为算法的性能互补性(performance complementarity)现象[1],与“没有免费午餐”(no free lunch)定理相印证[2]。算法的性能互补性现象普遍存在于不同领域,如何为给定问题从大量可行算法中选择满足应用需求的算法成为了各领域面临的重要挑战,即算法选择问题(algorithm selection problem)[3]。算法选择问题通常采用人工选择或自动选择的方法解决。人工选择方法通过实验试错或依赖专家选择合适的算法,然而实验试错方法成本较高,专家选择与专家的经验知识相关且灵活性较低[4]。自动选择方法通过设计算法和模型,根据问题的特点自动选择满足应用需求的算法,包括活跃测试(active test)方法、推荐系统方法以及基于元学习(meta-learning)的方法[5-7]。其中基于元学习的方法研究基础较为深厚,具备开销低和灵活度高等优点,成为了解决算法选择问题的主要方法[8-9]。
本文对基于元学习的算法选择进行综述总结,为研究人员了解相关领域的发展现状提供参考。
1 基于元学习的算法选择背景
本章介绍算法选择模型的概念,给出基于元学习的算法选择框架,详细说明框架的组成部分和一般流程,概括相关的综述工作。
1.1 算法选择模型
图1 给出了算法选择的抽象模型[10],模型包含四部分:(1)问题空间P,表示问题实例集合;(2)特征空间F,表示问题实例的可测度特征集合;(3)算法空间A,表示适用于所有问题实例的候选算法集合;(4)性能空间Y,表示对于给定的性能指标m,A中每个算法的性能集合。模型的具体流程为:对于具有特征f(x)∈F的问题实例x,找到一个到算法空间A的选择映射S(f(x)),使得所选算法α∈A在性能指标m上最大化性能映射y(α(x),m)∈Y。
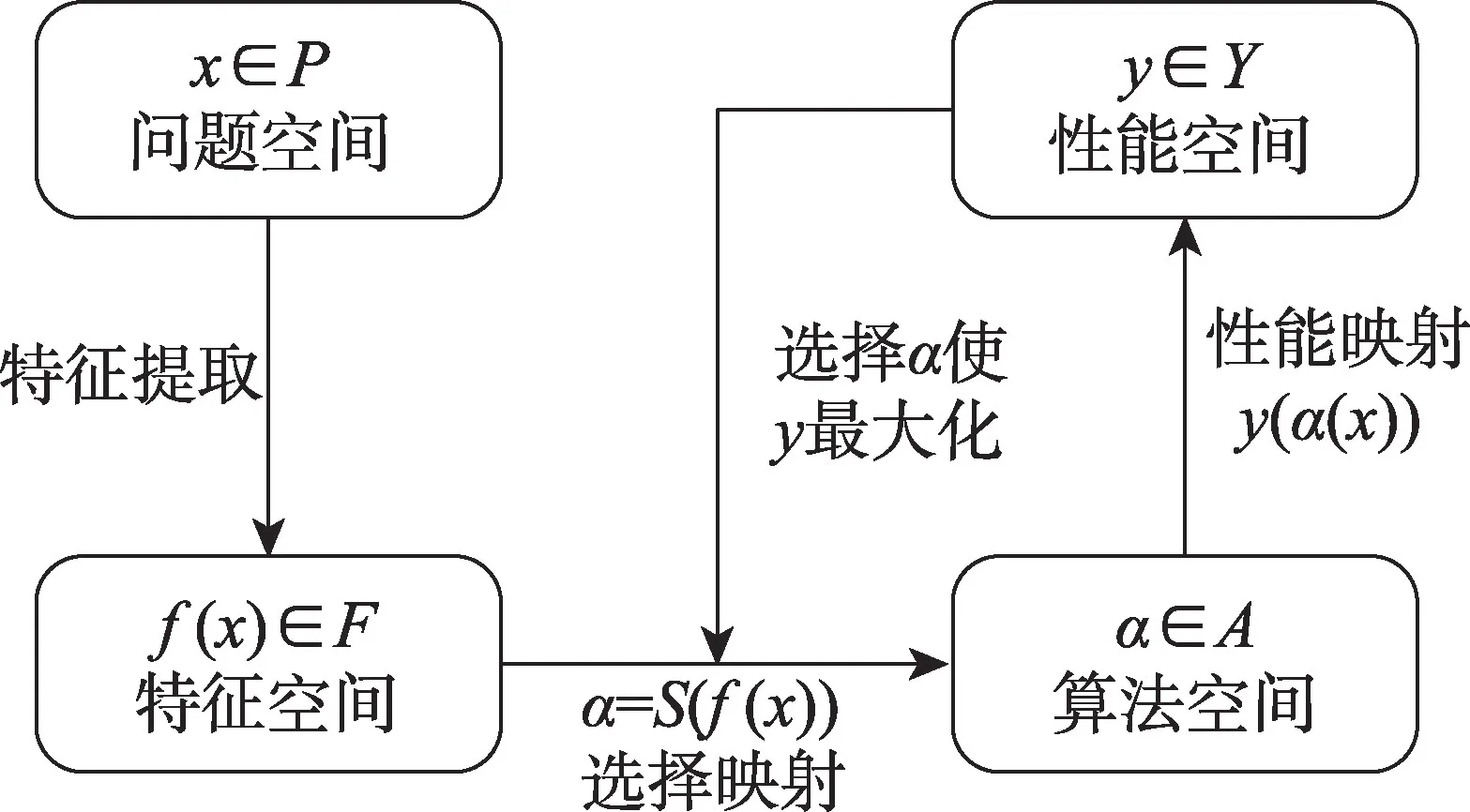
图1 算法选择抽象模型Fig.1 Algorithm selection abstract model
元学习即“学会学习的学习”,它利用历史学习经验进行学习,以达到适应新任务的目标[11]。元学习将算法选择问题视为常规的机器学习问题,通过机器学习算法构建问题特征与候选算法性能之间的映射关系[12]。在问题特征提取和映射构建等方面,基于元学习的算法选择已经形成了较为成熟的方法理论,是目前各学科领域中算法选择研究的热点方向[13-15]。
1.2 基于元学习的算法选择框架
在算法选择模型的基础上,基于元学习的算法选择一般框架如图2 所示[4,16]。框架包括元数据集(meta-dataset)构建和元模型(meta-model)训练两个主要阶段。元数据集构建阶段首先获取元知识(metaknowledge),包括元特征(meta-feature),即历史数据集可测度特征和候选算法在历史数据集上的性能;然后将算法选择问题转换为监督学习问题,结合元目标(meta-target),即算法选择目标,利用元知识构建元实例(meta-example)形成元数据集。具体地,元实例的属性为元特征,元实例的标签根据元目标和候选算法性能确定。元模型训练阶段应用元算法(meta-learner),即相应的监督学习算法,在元数据集上训练得到元模型。
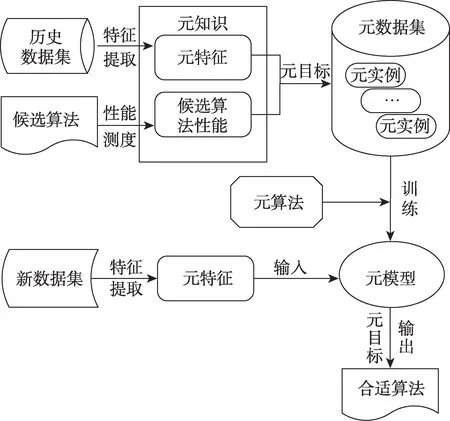
图2 基于元学习的算法选择框架Fig.2 Framework of algorithm selection based on meta-learning
对新数据集提取其元特征后,将元特征输入至已训练好的元模型,元模型根据给定的元目标预测并输出新数据集的合适算法。
元目标包括最优算法、算法排序和算法集合三种形式。最优算法和算法排序根据候选算法的性能指标值确定,其中算法排序分为全排序和部分排序,部分排序即全排序中前k个(top-k)性能最优的算法。算法集合则应用统计显著性检验方法确定,具体而言,检验其他候选算法与最优候选算法的性能差异显著性,将其中不存在显著性能差异的算法和最优算法视为合适算法构造算法集合[17]。
对于已训练好的元模型,通过元模型性能指标,计算给定元目标下历史数据集的历史算法信息与元模型预测算法结果的差异,即历史最优算法与预测最优算法、历史算法排序与预测算法排序、历史算法集合与预测算法集合之间的偏差,从而量化元模型的性能,检验算法选择方法的有效性。
1.3 相关工作
多年来,基于元学习的算法选择研究形成了丰富的文献,在此基础上,一些研究人员对其进行了综述总结。文献[10]首先介绍基于元学习的方法在分类算法选择中的发展成果,然后概述方法在诸如回归、优化等其他学科领域的拓展研究,并对方法跨学科应用的局限性和可行性进行了总结分析。文献[16]提出一个多学科通用的基于元学习算法选择框架,对元特征和元算法进行分类概述,最后从框架内容、学科领域等方面总结了问题与发展方向。文献[18]归纳整合元学习的不同定义,分析并指出元学习与算法选择的深刻联系,为基于元学习的算法选择方法提供了一定的理论依据。文献[19]简述元学习相关概念的发展历程,重点介绍了基于元学习算法选择方法在工作流设计和改进措施方面的发展,以及其在不同学科领域中的研究趋势。文献[4]提出基于元学习的分类算法选择框架,对相关的元特征和元算法进行分类综述,并通过实验对比不同类型元特征和元算法的应用效果。
区别于上述综述工作,本文总结近年基于元学习的算法选择研究,在对元特征和元算法进行分类的基础上,从不同角度分析并详细说明各类型方法的特性和优缺点;考虑算法选择方法的性能测度,对元模型性能指标进行分类描述,并对比不同指标的优缺点;以学习任务为出发点,归纳介绍方法的应用情况;通过实验定量分析不同类型元算法的优劣势与适用性;总结方法的现有问题和发展趋势,为后续研究提供参考。
2 基于元学习的算法选择研究进展
在基于元学习的算法选择方法中,元特征和元算法是影响方法性能的关键因素,而元模型的性能评估则是方法改进优化的重要参考。随着研究的深入,上述内容取得了一定的发展成果,出现了不同类型的方法。根据反映数据集特性的不同,可以将元特征分为基于统计和信息论、基于模型、基于基准和基于问题复杂度的方法;按照技术特点的不同,元算法可以分为基于规则、基于距离、基于回归和基于集成学习的方法;根据元目标的不同,可以将元模型性能指标分为基于最优算法、基于算法排序和基于算法集合的指标,如图3 所示。
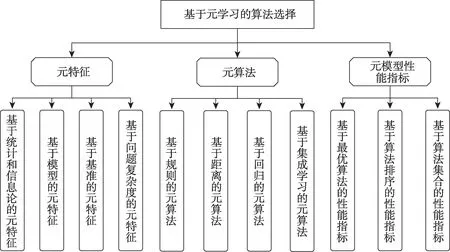
图3 基于元学习的算法选择研究内容与方法Fig.3 Research contents and methods of algorithm selection based on meta-learning
本章围绕元特征、元算法和元模型性能指标展开分析,分类并总结不同方法的优缺点。
2.1 元特征的研究进展
合适的元特征能充分反映数据集偏差,使元特征与算法性能的映射关系更精确,从而提升算法选择方法的性能,因此,如何提取并使用具备较强偏差反映能力的元特征成为了算法选择研究的主要问题。
分类算法选择是研究较为深入的领域,研究人员提出了多种分类问题元特征,其元特征提取思路和方法也被广泛借鉴和应用于其他学科的算法选择研究。本节以分类问题元特征为主,根据反映数据集特性和提取方法的不同,将元特征归纳为四类,分别是基于统计和信息论的元特征(statistical and information-theoretical based meta-features)、基于模型的元特征(model based meta-features)、基于基准的元特征(landmarking based meta-features)和基于问题复杂度的元特征(problem complexity based metafeatures),如表1 所示。
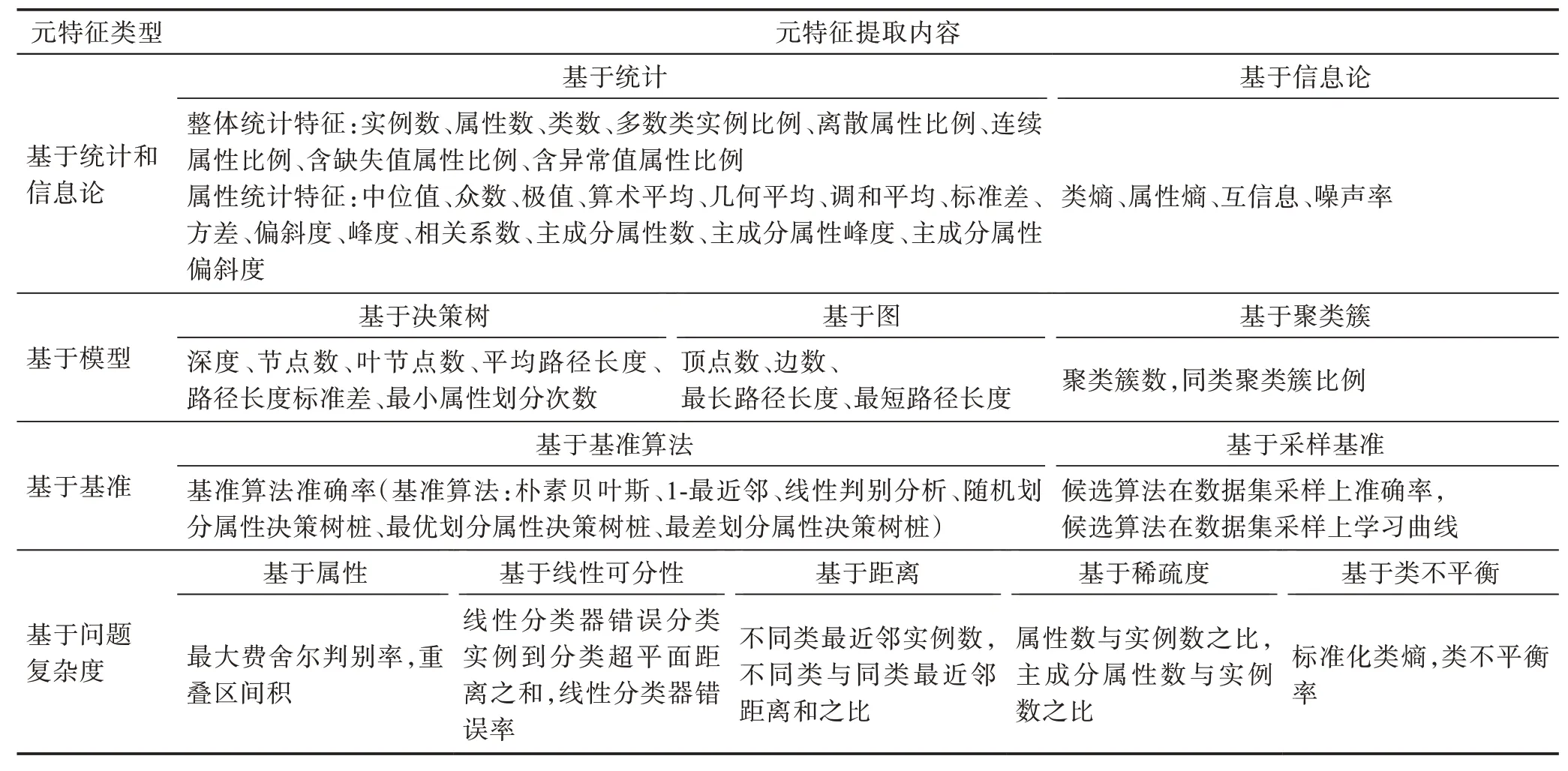
表1 元特征分类Table 1 Classification of meta-features
2.1.1 基于统计和信息论的元特征
基于统计的元特征和基于信息论的元特征是发展较为深入、应用较为广泛的元特征,在研究中常被合并使用,称为基于统计和信息论的元特征。统计特征包括数据集的整体统计特征和属性统计特征:整体统计特征包含数据集实例、属性以及类的统计信息,如数据集实例个数、属性个数、含缺失值属性个数等。属性统计特征反映数据集数值类型属性的中心趋势和离散程度[20],如属性的均值、方差、偏斜度(skewness)、峰度(kurtosis)等,偏斜度和峰度反映属性值分布的不对称情况和陡峭程度,其计算分别如式(1)和式(2)所示:
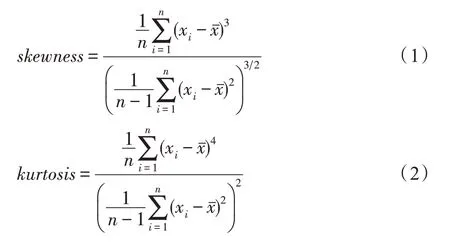
其中,n表示数据集的实例数,xi表示第i个实例的属性值,xˉ表示属性均值。基于信息论的元特征计算数据集枚举类型属性的熵、互信息、噪声率(noise signal ratio,NSR)等[21],反映属性的一致性和属性间的相关性,NSR 的计算如式(3)所示:

其中,(A)表示属性熵的均值,(C,A)表示互信息的均值,噪声率反映了分类数据集中冗余信息的比例,其值越小数据集越容易分类。值得注意的是,研究中常用均值或标准差对各属性的特征信息进行归纳,得到各属性峰度的均值、各属性熵的标准差等作为元特征。
大型分类算法比较项目STATLOG[22]首次使用了16 个基于统计的元特征描述分类数据集。在STATLOG 项目的基础上,研究人员引入基于信息论的元特征[21],扩展使用分类数据集中含缺失值属性、含异常值属性(异常值指属性的错误或不合理值)、属性分布频率、数据集主成分属性等的统计特征,扩充了元特征数量[23-25]。该类型元特征后续被广泛应用于其他学科的算法选择研究中,取得了较好的效果[26-28]。
2.1.2 基于模型的元特征
基于模型的元特征将数据集映射在不同结构的模型中,如决策树模型、图模型、聚类簇模型等,然后提取模型的结构属性作为元特征。
文献[29]总结了基于决策树模型的分类数据集元特征,该方法首先使用决策树算法在数据集上训练得到决策树模型,然后计算决策树的节点数、最大路径长度、划分属性出现次数标准差等作为元特征,反映数据集的整体特性。决策树模型中,决策树节点是数据集实例的集合,从包含全部实例的根节点开始,模型通过若干个分支节点评估数据集属性对类别的判别能力,选择判别能力较强者作为节点划分属性将节点实例集合划分到子节点,逐次划分直到叶节点完成分类决策,这样从根节点到叶节点的划分过程称为决策树路径。值得一提的是,该方法可使用不同算法生成决策树模型,所提取元特征的具体值也会随之变化。
文献[30]将数据集实例视为顶点,测度顶点之间的距离,使用边连接距离小于给定阈值的顶点,通过顶点的连接路径表示实例间的关系,使数据集映射为图模型,并以顶点、边、路径等的统计信息作为元特征,如顶点数、边数、最大路径长度等。
文献[31]首先使用基于贪心的聚类算法得到一个聚类簇集合,该集合中的聚类簇只包含同类别数据集实例且聚类簇之间互不相交,之后提取聚类簇的统计信息作为元特征,如聚类簇个数等。
2.1.3 基于基准的元特征
基于基准的元特征使用算法的性能指标值作为元特征。文献[32]提出以基准算法(实现简单且运行快速的分类算法)在数据集上的性能作为分类数据集元特征。其基本思想是:对于给定问题,候选算法与最优基准算法的学习偏差相近,则该候选算法更可能具备优越性能。基准算法应具备较低的计算成本和相异的学习偏差,因此,分类算法选择的研究中常用决策树桩(只有一个划分属性的决策树)、1-最近邻(1-nearest neighbor,1-NN)、朴素贝叶斯(naive Bayes,NB)、线性判别分析(linear discriminant analysis,LDA)等基准算法。
在基准算法的启发下,文献[33]提出以候选算法在原始数据集采样上的性能作为元特征,称为采样基准元特征。在此基础上,文献[34]以候选算法在原始数据集采样上的性能学习曲线为元特征,该性能学习曲线是采样规模以几何级数递增,算法性能随采样规模变化的曲线,由向量(ai,1,ai,2,…,ai,z)表示,其中ai,m表示候选算法a在第i个数据集的第m个采样上的性能。
针对聚类问题,文献[35]随机采样原始聚类数据集10%的实例形成子集,在该子集上应用DBSCAN(density-based spatial clustering of applications with noise)算法进行聚类,然后将聚类结果用作子集实例的标签,使其转换为分类数据集,最后计算基准算法在该分类数据集上的准确率(accuracy,Acc)作为元特征。
2.1.4 基于问题复杂度的元特征
基于问题复杂度的元特征是对数据集几何复杂度进行评估得到的元特征。根据提取方法的角度不同,可以将基于问题复杂度的元特征分为基于属性方法、基于线性可分性(linear separability)方法、基于距离方法、基于稀疏度方法和基于类不平衡(class imbalance)方法[36]。
基于属性方法通过数据集属性评估数据集的类重叠(class overlapping)程度(类重叠指不同类别的实例在某些属性上的值相近似),可计算得到最大费舍尔判别率(maximum Fisher discriminant ratio,MFDR)、重叠区间积(volume of overlapping region)等元特征。MFDR 是研究中常用的元特征,其计算各数值类型属性的费舍尔判别率(Fisher discriminant ratio,FDR),然后选择其中最大的FDR 值作为元特征,FDR 的计算如式(4)所示:
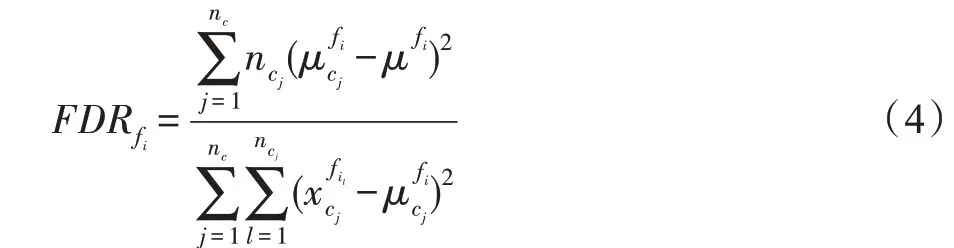
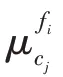
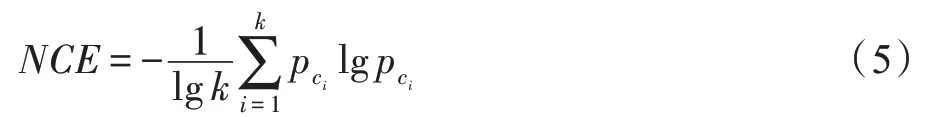
其中,k表示数据集类别的总数,pci表示第i类的实例比例,类别越平衡的数据集,NCE 值越大,当所有类别的实例数相等时,得到其最大值为1。
文献[37]通过数据集属性与标签的关联度、线性拟合度和实例的空间分布情况对回归问题的复杂度进行评估,得到回归问题的复杂度元特征。
针对聚类问题,文献[38]使用了基于距离的元特征,即计算数据集实例间的欧式距离,以距离的均值、峰度、偏斜度等统计信息作为元特征。
总结相关研究,可以发现元特征的3 个主要关注点:(1)充分反映数据集偏差;(2)充分体现不同算法的学习偏差,反映算法性能互补性;(3)降低元特征计算成本和获取难度。
基于统计和信息论的元特征在提取方法上易于理解和实现,然而其偏差反映能力较弱,研究中通常选取少数该类型元特征作为其他元特征的补充。基于模型的元特征提取方法相当于进行2 次特征提取,其首先通过算法训练模型提炼数据集的关键结构,在此基础上使用统计方法提取得到元特征,能够较好地反映数据集偏差。基于基准的元特征使数据集被映射在基准算法及其性能指标值所构成的空间中,量化数据集对不同算法的偏好程度,体现算法的学习偏差,应用效果较好。基于问题复杂度的元特征反映数据集的数据质量和解决问题的困难程度,这两方面与候选算法在数据集上的性能紧密关联,使该类元特征具备较强的偏差反映能力。
从计算复杂程度、提取方法的可扩展性和偏差因素三方面对不同类型的元特征进行对比分析,结果如表2 所示。

表2 元特征对比Table 2 Comparison of meta-features
基于统计和信息论的元特征计算简单且成本较低,但其度量数据集属性的统计和信息熵特性,难以充分反映数据集的整体特征,可扩展性相对较弱。基于模型的元特征将数据集映射在模型中,通过模型的结构属性描述数据集整体特征,方法的可扩展性较强,但是数据集映射和元特征提取的过程较为复杂。基于基准的元特征反映候选算法的学习偏差,然而算法性能的计算开销高昂,难以适应实时性要求较高的情况,且方法的可扩展性不强。基于问题复杂度的元特征测度数据集的空间分布复杂度,从类重叠、类决策边界、数据稀疏度、类不平衡等方面整体地描述数据集,具备较强的可扩展性,诸如ECol[39]等特征提取工具降低了元特征的获取难度,但其计算复杂度较大,且当数据集维度较高或存在缺失数据时,某些元特征的计算方法会失效。
2.2 元算法的研究进展
元算法是算法选择研究的关键之一,根据训练元模型的技术特点,可以将元算法分为四类:基于规则的元算法、基于距离的元算法、基于回归的元算法和基于集成学习的元算法。
2.2.1 基于规则的元算法
基于规则的元算法为每个候选算法生成选择规则,当元特征满足选择规则时,表示对应的候选算法为问题的合适算法。常采用C4.5、C5.0 等决策树算法建立数据集元特征与候选算法的关联,生成规则并凭此完成合适算法的决策。
STATLOG 项目使用决策树算法C4.5 作为元算法,生成22 个候选分类算法的选择规则。文献[40]以C5.0 决策树为元算法,通过对决策树的剪枝参数进行搜索优化,分别为8 个候选分类算法训练预测性能最好的决策树,生成各候选算法最优的选择规则,使构建的规则集合具备较高的可信度,图4给出了OneR(one rule)候选算法的选择规则示意,表示当数据集的实例数不小于1 728 且属性峰度的均值大于19.887 9时,OneR 算法为该数据集的合适算法。文献[41]使用213 个数据集和161 种元特征,以包括C4.5 在内的5 种元算法构建元模型,预测5 种特征选择算法的算法排序。针对负荷需求预测问题,文献[42]提取18 种数据集元特征,使用分类回归树(classification and regression tree,CART)算法从6 种候选算法中选择最优算法。
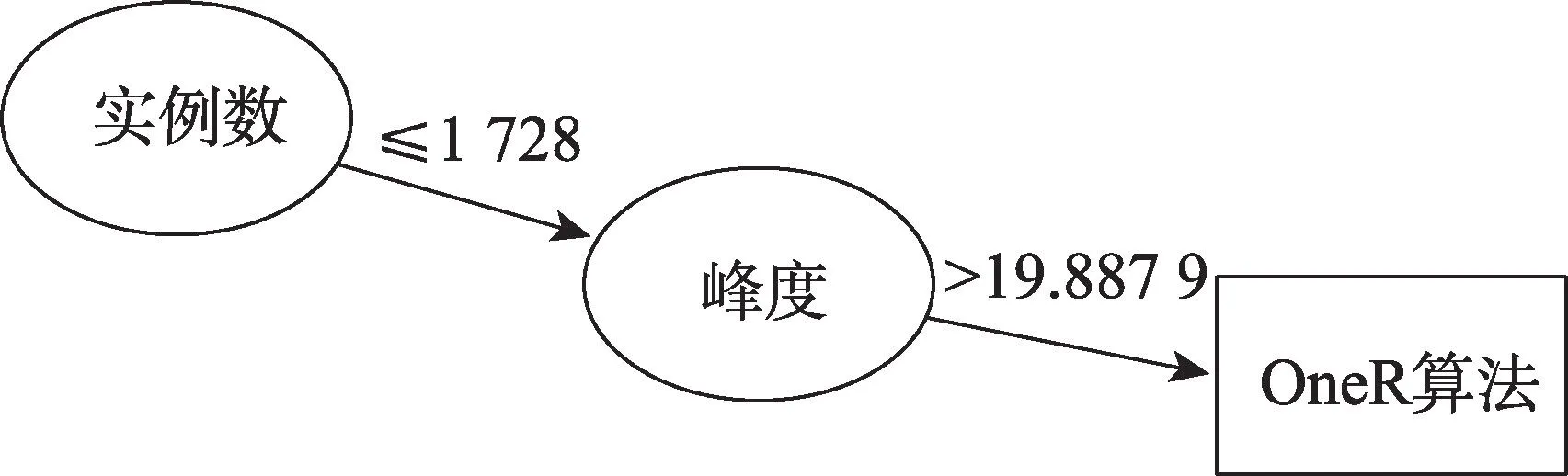
图4 候选算法选择规则Fig.4 Candidate algorithm selection rule
2.2.2 基于距离的元算法
基于距离的元算法利用元特征测度问题实例间的距离,对于新问题,利用与其距离最近的其他问题实例预测其合适算法。其基本思想是:算法在相似问题上的性能相近,而问题的相似度可以通过元特征距离进行量化计算。
在基于距离的元算法中,k-最近邻(k-nearest neighbor,k-NN)算法应用较为广泛。利用元特征对数据集特性的反映能力,可以将历史数据集映射在由元特征构成的空间中,提取新数据集的元特征后,k-NN 通过元特征测度其与历史数据集在上述空间中的距离,从中选择距离最近的k个历史数据集,然后基于这k个“邻居”的历史算法信息预测算法在新数据集上的性能表现。例如,当元目标为算法排序时,算法在新数据集上的预测排序由其在k个最相似历史数据集上的平均历史排序决定。k值和距离度量方法对于k-NN 的性能表现有着关键影响。文献[25]设置固定k值,对比分析了欧氏距离、曼哈顿距离、余弦距离和贾卡德系数4 种距离度量的应用效果,表示欧氏距离和曼哈顿距离的效果较好。文献[43]使用以距离倒数为权重的加权欧式距离,采用将所有元实例视为“邻居”的all-NN 构建元模型。文献[44]采用曼哈顿距离和80 个数据集进行实验,结果表明,使用不同类型元特征形成的元数据集,其对应的最优k值存在明显差异。文献[45]使用曼哈顿距离和2 700个数据集,对比了5-NN、10-NN、50-NN、500-NN 和all-NN 元算法的表现,其中50-NN 的性能较优。
少数研究使用了基于案例推理(case based reasoning)的方法构建算法选择系统[23,46]。在基于案例推理的系统中,元实例被表示为案例,元数据集被称为案例库,新数据集则对应新案例,通过案例检索、案例重用和案例学习的查询流程为新数据集选择合适算法并更新案例库。上述流程中,案例检索通过元特征测度案例间的距离,从案例库中检索相似案例;案例重用使用相似案例为新案例选择合适算法;案例学习评估查询的效果,将满足条件的新案例及其查询结果加入到案例库中。
2.2.3 基于回归的元算法
部分研究将算法选择问题映射为回归问题,应用回归算法训练元模型。具体而言,该方法生成以算法性能指标值为标签的元实例,为每个候选算法构建单独的元数据集;应用回归算法训练回归模型,对各候选算法的性能指标值进行预测;根据各算法的预测性能输出给定元目标的合适算法。
文献[47]提取27 种元特征,使用数据集元特征和候选算法的性能指标值为18 种候选算法分别构建元数据集后,对各元数据集采用线性回归(linear regression,LR)算法训练得到18 个回归元模型,通过元模型预测候选算法在新数据集上的性能指标值,形成预测算法排序。文献[37]使用支持向量回归(support vector regression,SVR)算法作为元算法,为14 个候选回归算法和2 类回归问题元特征分别构建了28 个回归模型,根据模型性能分析了2 类元特征的应用效果差异。文献[48]使用SVR 等3 种回归元算法,对5 种候选分类算法的性能指标值进行预测,根据预测偏差对不同类型元特征的应用效果进行对比。文献[49]对基于聚类簇的元特征开展实验研究,分别使用SVR、CART 等5 种回归元算法,预测5 种候选分类算法的准确率,分析表示基于聚类簇的元特征具备较强的偏差反映能力。
2.2.4 基于集成学习的元算法
该方法采用集成学习的思想,通过组合多个性能较弱的元模型(基学习器),得到具有较强泛化性能和算法选择性能的元模型。
随机森林(random forest,RF)是基于元学习的算法选择研究中广泛应用的元算法之一,它采用自助采样法生成若干训练数据集,在这些数据集上并行地训练决策树基学习器并加以组合。文献[50]首先使用时序预测模型拟合原始时序数据,通过模型生成与原始数据具有相似分布的模拟数据,共同构成历史数据集;然后,对于历史数据集中的每一份时序数据,提取其32 种时序元特征,将其划分为训练时间段和测试时间段,训练9 种时序预测模型并根据测试性能确定最优模型,以元特征为属性,以最优模型为标签形成元实例构建元数据集;最后使用RF 元算法训练元模型,对于新时序数据,提取其元特征,使用元模型对其最优时序模型进行分类预测。文献[51]通过强化学习从多种元特征中选择合适的元特征子集,建立元数据集并使用RF 训练元模型,从4 种分类算法中选择最优算法。文献[52]针对多目标回归问题,基于RF 构建元模型,从2 种回归算法和6 种多目标回归问题转换方法中选择合适的组合。
极端梯度提升(extreme gradient boosting,XGB)算法顺序训练并组合若干个基学习器,具体而言,在训练过程中,算法根据上一个基学习器的表现调整训练数据的分布,以提升当前基学习器的学习性能,当基学习器数量达到阈值时按照顺序组合所有基学习器。文献[53]使用10 种聚类性能指标测度17 个聚类算法的性能,通过单独使用和结合使用10 种指标的方法构建11 个元数据集,在构建元数据集时,每一个历史数据集和候选算法的成对组合对应一个元实例,该元实例由历史数据集的元特征、候选算法在该数据集上的历史排序以及用于表示该候选算法的离散值构成;采用排序学习策略的XGB 训练元模型,输入新数据集的元特征后,元模型即可以生成各候选算法的预测排序。文献[54]利用大量已有的分类算法研究成果,将算法性能和数据集的相互关系通过向量嵌入(vector embedding)方法表示为元特征,然后基于XGB 生成元模型,验证该元特征的使用效果。文献[55]设计可应用于分类或回归问题的算法选择系统AutoGRD,该系统为分类和回归任务设置了不同的XGB 元算法参数,并通过对比实验展示了系统的适用性。
除上述元算法外,个别研究使用生成对抗网络(generative adversarial network)构建元模型[56-57]。然而,该深度学习方法需要大量具备统一格式的训练数据,在历史数据集的收集和处理以及元数据集的构建方面均存在较大问题,难以泛化应用。
表3 展示了不同类型元算法的优缺点。
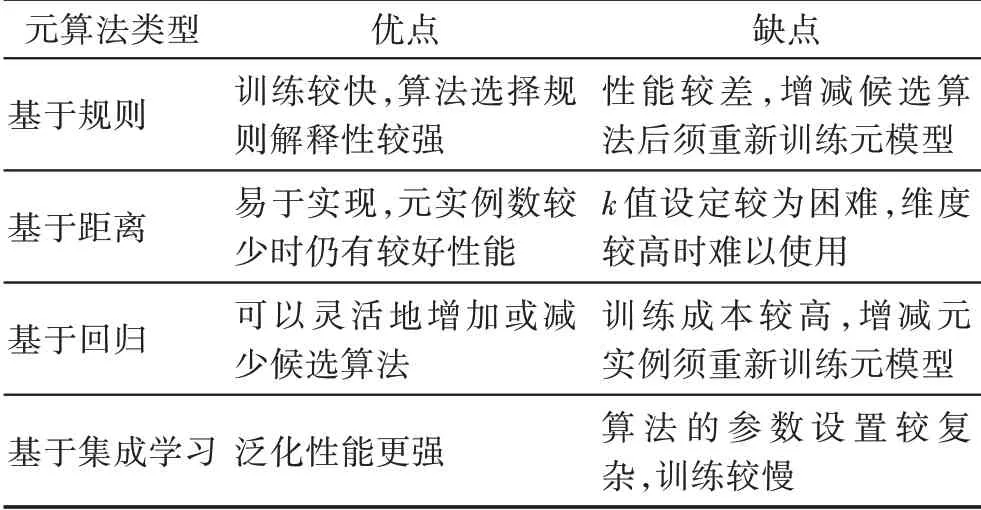
表3 元算法优缺点对比Table 3 Comparison of advantages and disadvantages in different meta-learners
基于规则的元算法生成候选算法的选择规则,可解释性较好,但在增减候选算法时需要重新训练元模型,灵活性不足。基于距离的元算法易于实现,在元数据集的规模较小时仍具备较好的性能,然而算法的最优k值受多种因素影响,设置较为困难,且算法在元数据集维度较高时难以使用。基于回归的方法在增减候选算法时较为灵活,不会影响已训练的回归模型,但是训练多个模型的成本较高,且元实例数变化时需要重新训练所有模型。基于集成学习的元算法相对于单个元算法常有更优表现,然而复杂的参数设置使元模型的调优更具挑战性,此外,基学习器的设置是该方法的关键,不同基学习器的应用效果仍待探究。
元目标是选用元算法的关键参考,现结合元目标对元算法做进一步分析。基于规则的元算法常用于预测最优算法,该方法训练较快,生成的规则有利于对元特征进行深入分析,然而其泛化性能较差,应用较为有限。基于距离的元算法训练过程不受元实例标签的影响,易于实现且应用灵活,是算法排序研究中的经典方法,同时也适用于其他元目标,但是设置最优k值的难题限制了其快速应用,而性能表现也是其短板之一。根据候选算法的预测性能指标值,基于回归的元算法可以间接完成不同元目标,且算法选择结果易于理解,然而多个模型的调整成本和整体误差较高。基于集成学习的元算法通过设置基学习器和学习策略可适用于不同元目标,其具备较强的泛化性能和适用性,在近年的研究中更受青睐,但训练速度较慢。
2.3 元模型性能指标的研究进展
元模型的性能评估是算法选择研究的一项重要内容,而其中的关键问题是采用何种性能度量指标。本节根据元目标和元模型输出结果的不同,将元模型性能指标分为基于最优算法指标、基于算法排序指标和基于算法集合指标,如表4 所示。

表4 元模型性能指标Table 4 Performance measures of meta-model
2.3.1 基于最优算法指标
预测最优算法常被视为分类任务,在这种情况下,分类性能指标对于元模型性能评估具有天然的适用性,如准确率指标和基于混淆矩阵的指标。此外,推荐准确率(recommendation accuracy,RA)指标也是研究中常用的指标之一。
准确率指标计算预测最优算法与历史最优算法相一致的元实例在若干测试元实例中所占比例,是应用较为广泛的经典指标。
对于类不平衡元数据集,即不同历史最优算法类别的元实例数量差距较大的元数据集,准确率难以评估元模型对少数类的预测效果,对此,许多研究选用如下所述基于混淆矩阵的指标。
考虑元模型从两种候选算法(不妨设为正例候选算法和反例候选算法)中为测试元实例预测最优算法的情况,其预测结果的混淆矩阵如表5 所示。

表5 最优算法预测结果混淆矩阵Table 5 Confusion matrix of prediction results of best algorithms
表5 中,真正例(true positive,TP)表示正确预测正例候选算法为最优的元实例数,假反例(false negative,FN)表示错误预测反例候选算法为最优的元实例数,真反例(true negative,TN)表示正确预测反例候选算法为最优的元实例数,假正例(false positive,FP)表示错误预测正例候选算法为最优的元实例数。
基于混淆矩阵,查准率(precision,Pre)、查全率(recall,Rec)、假正例率(false positive rate,FPR)和特异度(specificity)指标的计算如式(6)~式(9)所示,其中查全率也被称为真正例率(true positive rate,TPR)或灵敏度(sensitivity)。
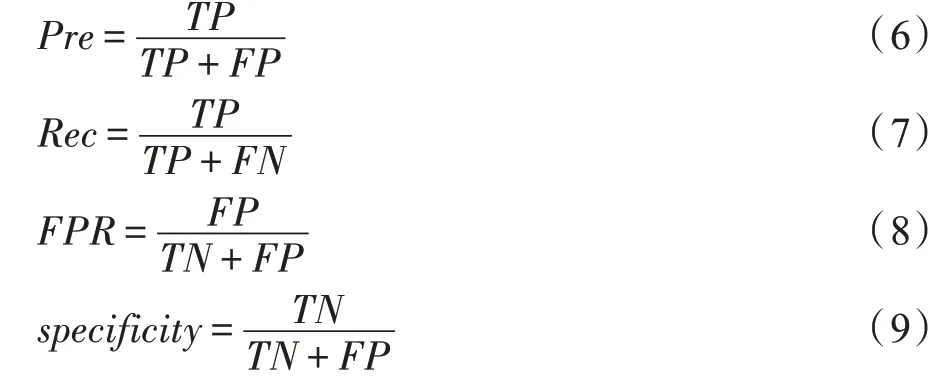
F1 得分是上述查准率和查全率的加权调和平均,其计算如式(10)所示:

基于TPR和FPR,可以计算得到AUC(area under curve)性能指标,如式(11)所示:

平衡准确率(balanced accuracy,BA)指标计算灵敏度和特异度的均值,如式(12)所示:
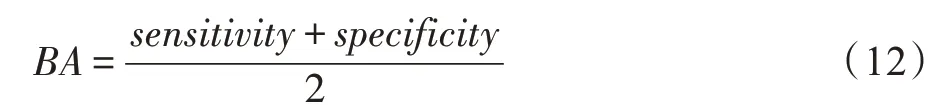
文献[24]提出RA 指标,其度量预测最优算法与历史最优算法的性能差距,如式(13)所示:

其中,PAp,D和PAb,D分别表示在给定数据集D上的预测最优算法与历史最优算法的性能,PAw,D表示数据集D上历史最差算法的性能,该历史最差算法根据元知识中的候选算法性能信息确定。
2.3.2 基于算法排序指标
对算法排序结果进行评估的指标包括斯皮尔曼排序相关系数(Spearman rank correlation coefficient,SRC)、平均排序倒数(mean reciprocal rank,MRR)和排序命中率(hit ratio,HR)。
SRC 测度预测算法排序和历史算法排序的相似度,可以较为准确地评估算法全排序的结果,其计算如式(14)所示:
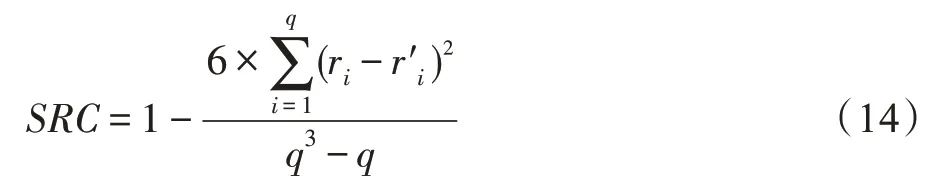
其中,q为候选算法数,ri和分别表示第i个候选算法在预测算法排序和历史算法排序中的位置。SRC值为[-1,1],其值越大表示元模型的预测结果越精确。
历史最优算法在预测算法排序中的排序位置是研究人员较为关心的结果,MRR 即通过历史最优算法快速地评估算法排序效果,其计算如式(15)所示:

其中,m为数据集数,branki表示数据集i的历史最优算法在预测算法排序中的排序位置,MRR值越大表明元模型性能越好。
针对输出算法部分排序的元模型,常用排序HR指标测度其性能,该指标对元模型预测算法的可用性进行简要评估,其计算如式(16)所示:

其中,m为数据集数;对于数据集i,其历史算法排序中的前k个最优算法构成一个集合,预测算法部分排序中的k个算法构成另一个集合;当上述集合的交集不为空时,HitCounti值为1,表示预测“命中”,反之,HitCounti值为0,表示“未命中”。随着k值增加,预测更容易“命中”,命中率随之提高。
2.3.3 基于算法集合指标
在以算法集合为元目标的研究中,常用向量(a1,a2,…,aq)表示算法集合,其中ai值为1 表示第i个候选算法为合适算法,为0 表示非合适算法,使用的元模型性能指标包括排名损失(ranking loss,RL)、汉明损失(Hamming loss,HL)和集合HR。
文献[58]预测算法为合适算法的概率并根据概率对算法排序,当概率超过给定阈值时将算法并入预测算法集合,从而同时获取预测算法集合和预测算法排序;当合适算法的排序比非合适算法的排序大时,则预测错误,由此可以通过RL 指标计算历史算法集合中的合适算法被错误预测次数,如式(17)所示:
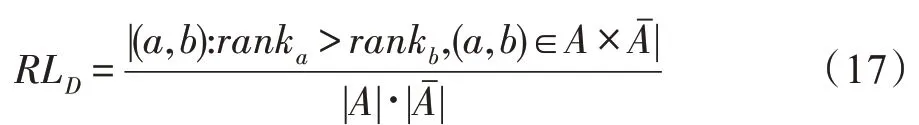
其中,A和表示数据集D上的历史算法集合及其补集,ranka和rankb分别表示算法a∈A和算法b∈Aˉ在预测算法排序中的排序位置。RL 指标值越小,说明元模型的错误预测次数越少,其性能越强。
HL 指标利用算法集合向量元素值的二元性质,计算预测算法集合与历史算法集合向量的差异程度,如式(18)所示:

其中,q为候选算法数;对于数据集D,PD表示预测算法集合,TD表示历史算法集合;Δ 表示逐个对比PD和TD的对位元素,若相异则PDΔTD值加1。HL指标值越小表示元模型性能越好。
集合HR 与排序HR 指标计算方法一致,区别在于历史算法集合固定,集合HR 不受参数k影响。集合HR 值越大,元模型的表现越好。
此外,在使用回归元算法的研究中,均方误差(mean squared error,MSE)和均方根误差(root mean squared error,RMSE)指标被用于测度元模型性能,其计算回归模型的性能指标值预测误差,分别如式(19)和式(20)所示:
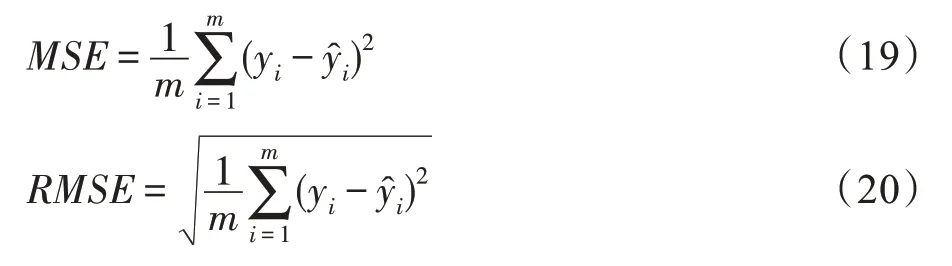
其中,m表示数据集数;对于数据集i,yi表示元知识中候选算法的历史性能指标值表示候选算法的预测性能指标值。
表6 总结了不同元模型性能指标的优缺点。
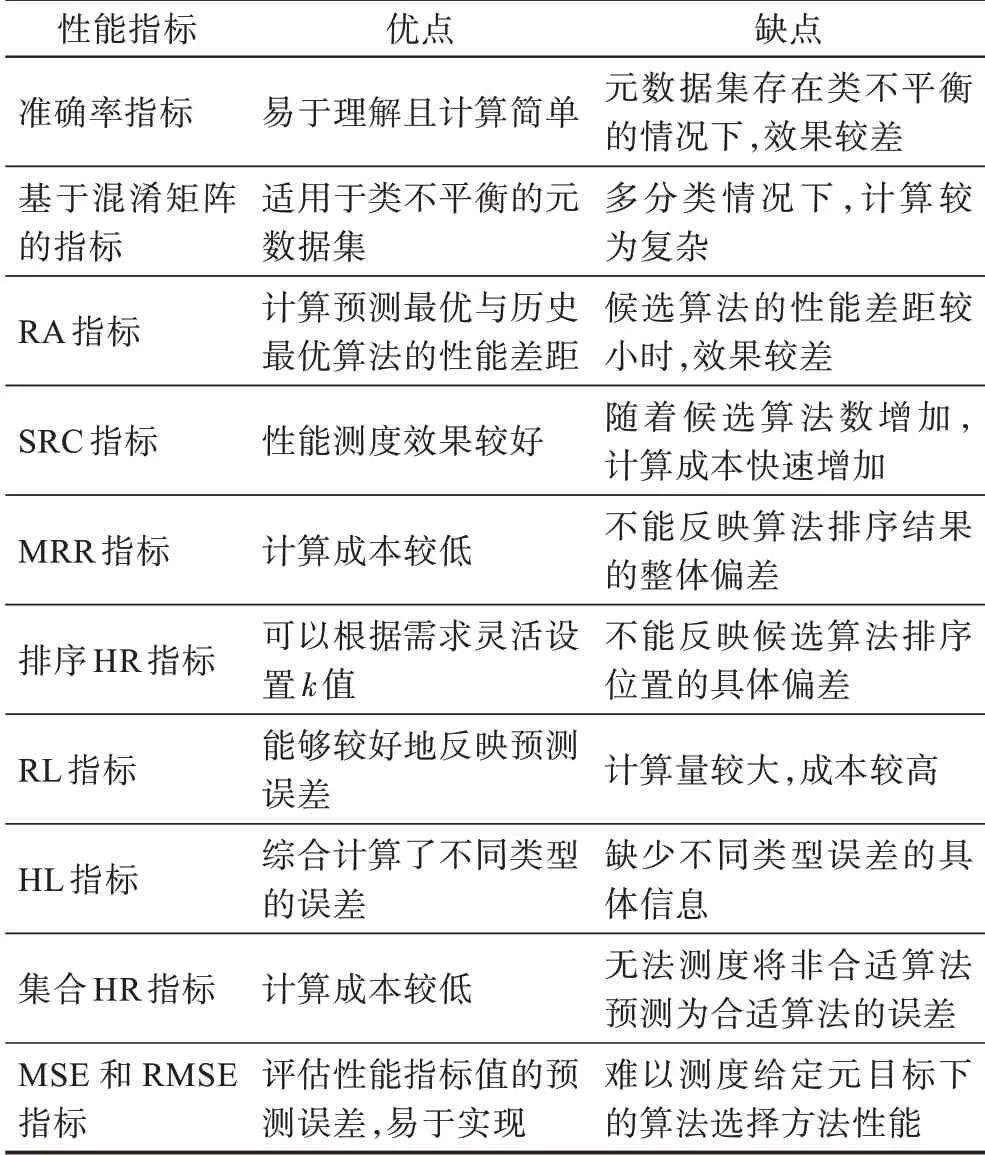
表6 元模型性能指标优缺点对比Table 6 Comparison of advantages and disadvantages in different meta-model performance measures
基于最优算法的指标中,准确率指标应用广泛,计算简单,但当元数据集存在类不平衡时难以反映元模型的综合性能;相较于准确率,查准率、查全率、F1 得分等基于混淆矩阵的指标考虑了正负例的预测性能,更适用于类不平衡的元数据集,但指标在多分类情况下的计算较为复杂;RA 指标计算预测最优算法和历史最优算法的归一化性能差距,然而在候选算法的性能差距较小时,该指标的效果较差。
基于算法排序的指标中,SRC 指标能够有效度量算法排序结果的偏差程度,但随着候选算法数增加,其计算成本也快速增加;MRR 指标计算简单,但是指标忽略了除最优算法外的其他候选算法,不能反映算法排序结果的整体偏差;排序HR 指标可以根据需求设置不同k值,较为灵活,然而该指标不能反映候选算法排序位置的具体偏差。
基于算法集合的指标中,RL 指标能较好地反映预测结果的误差,然而其计算量较大;HL 指标考虑了将合适算法预测为非合适以及将非合适算法预测为合适的两类误差,提供了综合性的评估结果,但是不能提供不同误差的明确信息;集合HR 指标易于计算,然而其无法衡量将非合适算法预测为合适算法的误差程度。MSE 和RMSE 指标评估性能指标值的预测误差,易于实现,但是在给定元目标下,两种指标难以评估算法选择方法的有效性。
3 基于元学习的算法选择应用
为了降低对数据进行分析决策的成本,研究人员广泛使用了基于元学习的方法进行算法选择。本章根据使用数据集类型和学习任务的不同,将算法选择研究分为分类应用、回归应用和聚类应用。考虑具体的应用内容,近年的算法选择研究应用情况如表7 所示。

表7 基于元学习的算法选择应用Table 7 Application of algorithm selection based on meta-learning
3.1 分类应用
分类问题是算法选择重要的研究方向,出现了大量的研究文献。为了构建具备一定规模的元数据集,提供更可信的算法选择结果,多数研究广泛使用来源于不同应用领域的分类数据集和不同种类的候选分类算法,并基于不同类型的元算法训练元模型完成算法选择[17,31,48]。自动机器学习(automated machine learning)是相关研究的热点之一,其通过算法选择和超参数优化等多个流程为给定任务构建最优机器学习模型[59-60]。部分研究采用基于元学习的方法从多个候选算法中选择部分较优算法,在此基础上,对所选算法进行超参数优化以减少整体时间开销。文献[61]选用12 种候选分类算法,采用k-NN 从中筛选较优算法进行超参数优化。文献[62]基于候选算法性能设计一种比较规则,根据规则为每个数据集确定较优算法,并采用决策树算法构建元模型。文献[63]在上述研究的基础上,针对自动机器学习的可扩展性问题,提出了一种分布式自动机器学习框架,实验表明该框架在大型数据集上具备较优性能。
随着各领域数据量的增加和方法技术的扩展,聚焦于特定领域的算法选择研究逐渐增多。在生物分析领域中层次分类(hierarchical classification)问题较为常见,其数据集的类别之间存在层次关系,文献[64]提出27 种层次分类数据集元特征,采用J48 决策树算法训练元模型,生成层次分类算法的选择规则。文献[65]面向网络安全领域中的网络攻击检测问题,通过SVR 元算法训练元模型,预测5 种候选分类算法的查全率并据此完成算法排序。
在针对图像数据进行分析的研究中,文献[66]采用卷积神经网络(convolutional neural network,CNN)提取图像元特征向量,在此基础上使用RF 训练元模型,选择用于图像分类任务的最优CNN 模型。图像分割对图像进行像素级别的分类,是图像数据处理中的重要步骤,文献[67]从色彩、质量、纹理等多个方面提取图像元特征,对比了3 种元算法的算法选择效果,其中RF 元算法的性能更优。针对医学影像的图像分割任务,文献[68]使用CNN 提取图像元特征,通过基于回归的方法预测深度学习模型的图像分割性能。
部分研究为分类数据集选择数据处理技术。分类数据集类不平衡问题可以通过多种数据集采样方法加以解决,如过采样、欠采样等,文献[44,69]首先确定用于类不平衡数据集的分类算法,在此基础上采用基于元学习的方法为数据集选择合适采样方法,提升分类算法的性能。异常检测(anomaly detection)技术是提升数据集数据质量的重要手段,在诸多领域中得到了重视。文献[70]提出5 种异常数据元特征,使用基于元学习的方法选择最优异常检测算法,验证所提元特征的应用效果。文献[71]针对航空设备故障诊断数据的高维问题,以选择最优特征选择算法为目标,设计基于元学习的算法选择系统以避免遍历特征选择算法的时间和空间成本。文献[72]对基因表达数据分析展开研究,设计从4 种特征选择算法和3 种分类算法中选择最优组合的算法选择方法,对比实验了神经网络、轻量梯度提升机(light gradient boosting machine)和k-NN 元算法的性能差异,结果显示神经网络和轻量梯度提升机均优于k-NN。
此外,文献[73]考虑集成分类算法在人类活动识别系统中的应用,基于k-NN 元算法为集成分类器选择最优集成剪枝(ensemble pruning)算法,对集成分类器中的基学习器进行修剪筛除,从而降低应用集成分类算法的计算开销。
3.2 回归应用
回归与分类均为有监督学习问题,在数据集属性等方面具有一定的相似性,文献[37]受到分类元特征研究的启发提出回归数据集元特征,文献[46,55]则设计可以兼顾分类和回归任务的算法选择系统。
算法选择研究在回归应用中也呈现出一定的领域针对性。定量构效关系(quantitative structure activity relationship)表示化合物分子结构和化合物活性之间的映射关系,文献[45]分析定量构效关系学习问题中药物成分和蛋白质靶标的特征,采用基于元学习的方法选择最优回归算法。文献[74]基于元学习方法设计算法选择框架,采用RF 元算法形成15 个候选回归算法的算法排序,为数据科学家在大数据分析过程中提供决策助力。
基于时序数据的回归预测是不同领域中的重要任务[50]。文献[42]重点研究外部天气因素对短期电力负荷需求的影响,基于此提出相应的元特征并开展算法选择研究。针对电力消耗预测问题,文献[75]分别采用了k-NN、RF 等5 种元算法生成元模型,从4种时序预测算法中选择最优算法,其中RF 具备优异表现。文献[76]以能源消耗预测为应用领域,考虑时序数据中的时间属性,结合汇总统计方法提出基于时间属性的元特征,并通过聚类方法分析该元特征的使用效果。在文献[76]的基础上,文献[77-78]使用多种时序数据集元特征,结合大数据和微服务技术,构建基于元学习的时序预测算法选择框架。正确评估软件在一定时间段内发生故障失效的概率可以降低软件测试、维护和发布的成本,文献[79]提出4 种元特征描述软件故障数据,分别采用J48 决策树和神经网络作为元算法,从5 种软件可靠性分析模型中选择最优模型。
推荐系统(recommendation system)旨在通过推荐算法建立用户与项目之间的关系,预测用户对项目的评分,从而为用户推荐感兴趣的项目。文献[80]结合聚类方法构建推荐算法选择系统,其首先通过k均值(k-means)聚类算法将用户推荐数据集划分为10个聚类簇,然后根据推荐算法在聚类簇各实例上的平均性能为聚类簇选定最优推荐算法。最后,基于1-NN 为新数据集确定最近邻的聚类簇,得到最优算法的预测结果。文献[81]在使用14 个用户推荐数据集和3 种推荐算法构建元数据集的基础上,根据14 个元实例的统计数据合成新的元实例扩充元数据集,分别应用了4 种元算法进行实验。文献[82]将推荐算法在用户推荐数据集上的排名线性转换为评分作为算法元特征,结合数据集元特征构建元数据集,实验对比了3 种元算法的性能表现。
3.3 聚类应用
相较于算法选择在分类和回归任务中的应用,面向聚类问题的算法选择研究相对较少。文献[26]使用10 种候选聚类算法和11 种聚类性能指标展开研究,其利用元实例的元特征信息,通过聚类算法划分元实例的聚类簇并选出簇的原型,然后采用1-NN 为新数据集选择与其元特征距离最近的原型,使用原型所对应的单个元实例或元实例聚类簇完成算法选择决策。文献[35]使用7 种聚类算法和4 种聚类指标进行实验,对k-NN 与DeepFM 深度学习模型的算法排序性能进行对比,结果显示DeepFM 的性能较优。文献[38]选用10 种聚类算法和13 种聚类指标设计算法选择实验,将所提元特征与其他3 类元特征进行对比分析,结果验证了所提元特征对聚类数据集特性具有良好的反映能力。文献[83]面向在线算法服务问题,考虑运行时间和准确率两种算法服务质量,采用分类元算法为用户选择最优聚类算法,采用回归元算法预测聚类算法的服务质量为用户提供算法排序。文献[84]通过基于回归的方法构建元模型预测8种聚类算法的性能指标值,分析25 种聚类问题元特征的应用效果。
个别研究考虑聚类算法中的关键参数,通过基于元学习的方法进行选择设置。文献[13]从9 种距离度量方法中进行选择,通过RF 元算法预测最优距离度量方法,采用k-NN 元算法预测距离度量方法的排序,分别为两种聚类算法确定其在不同数据集上的合适度量方法。文献[28]以聚类算法的聚类簇个数设置为研究点,提出一种元特征向量描述聚类数据集的数据密度,通过基于回归的方法预测聚类算法在设置不同聚类簇个数时的性能指标值,为算法确定其最优聚类簇个数设置。
4 实验分析
为了比较不同类型元算法的性能并分析其适用性,本章通过分类算法选择实验对元算法的算法选择性能进行量化对比。
4.1 实验设置
考虑到实验的可参考性,数据集、元特征、候选算法、元目标等均采用现有研究中常见的设置,具体如下所述。
使用来自UCI、KEEL 和StatLib 的140 个分类数据集,这些数据集在数据来源领域、实例个数、属性个数和类型等方面具有一定的差异性,构成多样化的数据集,从而能够有效评估元算法的性能。实验数据集信息如表8 所示。为了使元特征能够提取并反映数据集的原始特性,实验暂不考虑数据质量对算法性能的影响,不对数据集进行数据预处理。
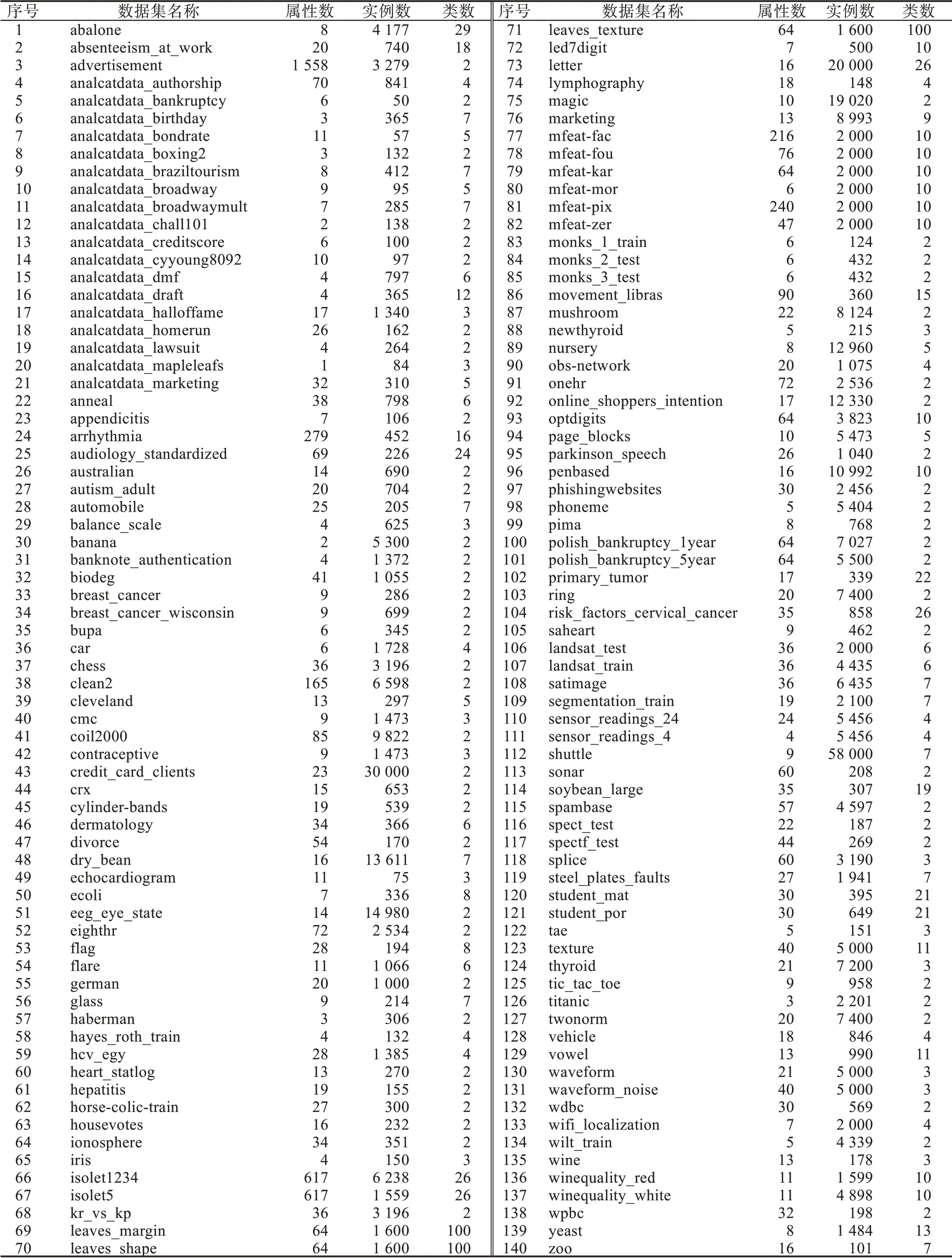
表8 实验数据集信息Table 8 Information of experiment datasets
通过元特征提取工具MFE[12]提取数据集的150种元特征,包括77 种基于统计和信息论的元特征、24种基于模型的元特征、14 种基于基准的元特征和35种基于问题复杂度的元特征。
使用8 种sklearn[85]机器学习平台的分类算法作为候选算法,包括k-NN、RF、支持向量机(support vector machine,SVM)、逻辑回归(logistic regression,LoR)、NB、LDA、C4.5 决策树和多层感知机(multilayer perceptron,MLP),均采用sklearn 中的默认参数设置。MLP 是深度学习中的经典算法之一,而深度学习中所令人熟知的代表性技术是CNN。为提供较为全面的参考,本文基于Keras[86]构建CNN 模型,出于实现的简易性和对不同数据集的适用性考虑,使用一个含有32 个卷积核的一维卷积层、一个全连接层以及一个最大池化层构成CNN 的隐藏层。此外,设置卷积层和全连接层使用ReLU(rectified linear unit)激活函数,输出层使用Softmax 激活函数。
以最优算法为元目标,通过5 次10 折交叉验证计算各候选算法在实验数据集上的准确率、查准率、查全率、F1 得分和ARR(adjusted ratio of ratios)[87]指标值,确定各数据集的最优算法,构建5 种指标对应的元数据集。上述指标中,ARR 综合考虑算法的准确率和运行时间,其计算如式(21)所示:
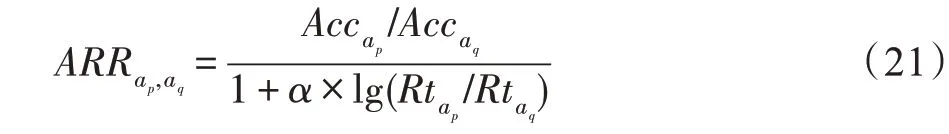
其中,ap和aq表示候选算法;Acc和Rt表示算法在数据集上的准确率和运行时间;α为可变参数,表示准确率和运行时间的相对重要程度,α值越大则运行时间越重要。实验中ARR 的α参数取值包括研究中常用的0.1、0.01 和0.001,以获取更全面的算法性能比较结果。
采用sklearn 中默认参数设置的C4.5、CART、k-NN、LR、SVR、RF 和XGB 作为元算法,通过留一法交叉验证获取元算法的准确率、查准率、查全率、F1 得分和推荐准确率性能指标值。
4.2 实验结果与分析
分别用MAcc、MPre、MRec和MF1代表准确率、查准率、查全率和F1 得分指标对应的元数据集,使用MA1、MA2和MA3表示ARR 指标在α值分别取0.1、0.01 和0.001 时生成的元数据集,各元数据集中各候选算法的胜出次数如表9 所示。从表9 可以看出,RF候选算法仅在MA1元数据集上的胜出次数较少,可见其具有优越的分类性能,但是运行时间是其较为明显的短板。与RF 相对的是k-NN 和NB,得益于算法较快的运行速度,其在ARR 指标上具备一定优势,但分类性能较差,因此,随着α值的减小,运行时间的重要性降低,二者在ARR 元数据集中的胜出次数减少。SVM 和LoR 的分类性能较优且具有合适的时间开销,在5 种指标上均取得了较好结果。LDA 和C4.5的分类性能强于k-NN 和NB,另一方面,两种候选算法在ARR 指标上也具有优良表现,说明其在运行时间和准确率两方面较为均衡。MLP 和CNN 在各数据集上的运行时间最长,但二者在部分数据集上的分类性能具有一定优势,因而在MA2和MA3上仍取得了一定次数的胜出。
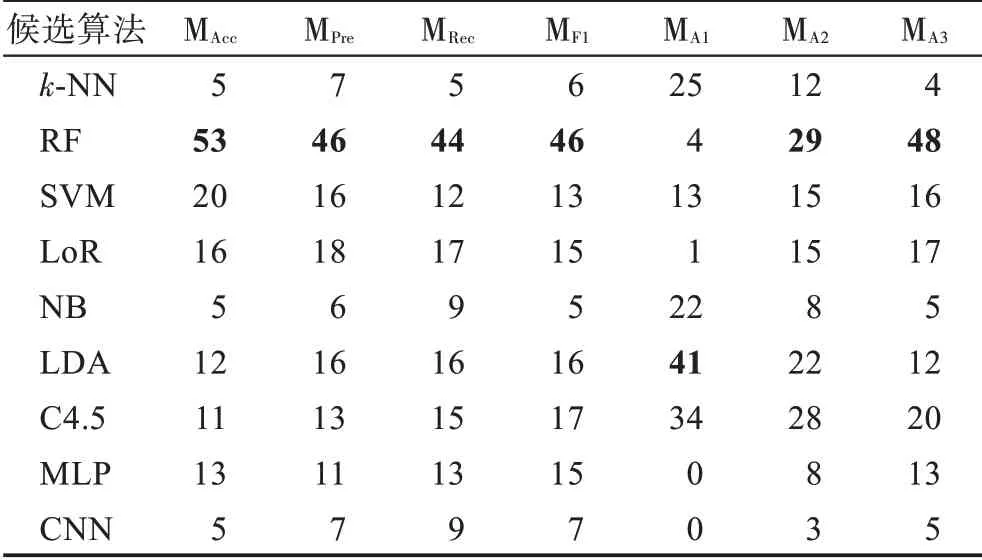
表9 候选算法胜出次数Table 9 Win times of candidate algorithms
元算法在各元数据集上的准确率、查准率、查全率、F1 得分和推荐准确率指标值如表10~表14 所示。
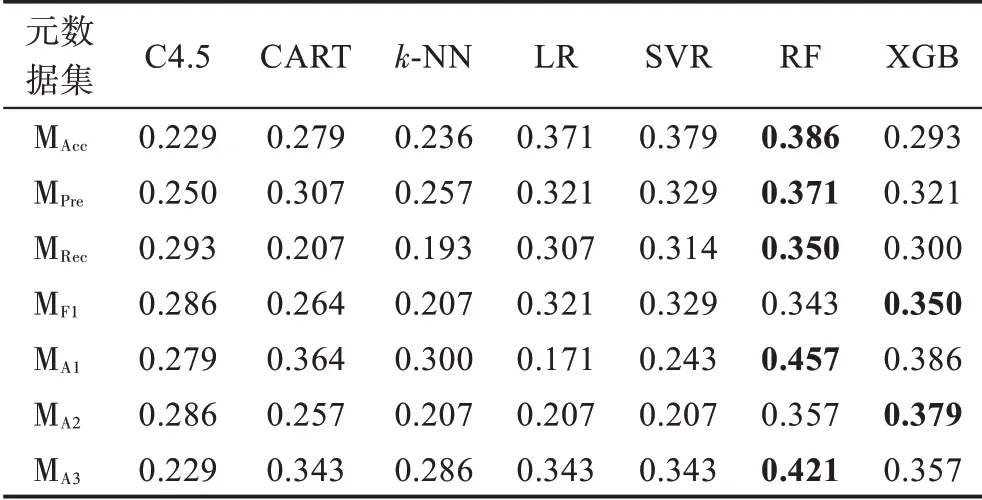
表10 元算法准确率指标值Table 10 Accuracy value of meta-learners
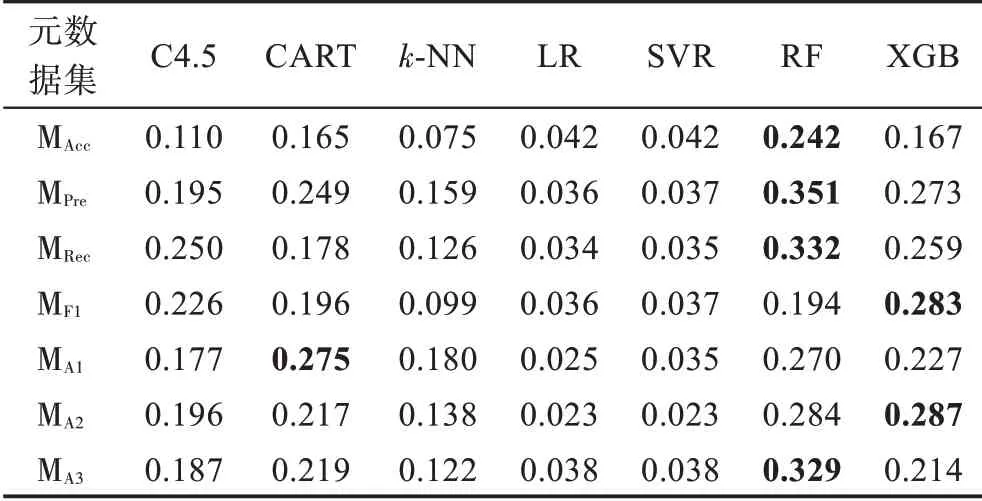
表11 元算法查准率指标值Table 11 Precision value of meta-learners
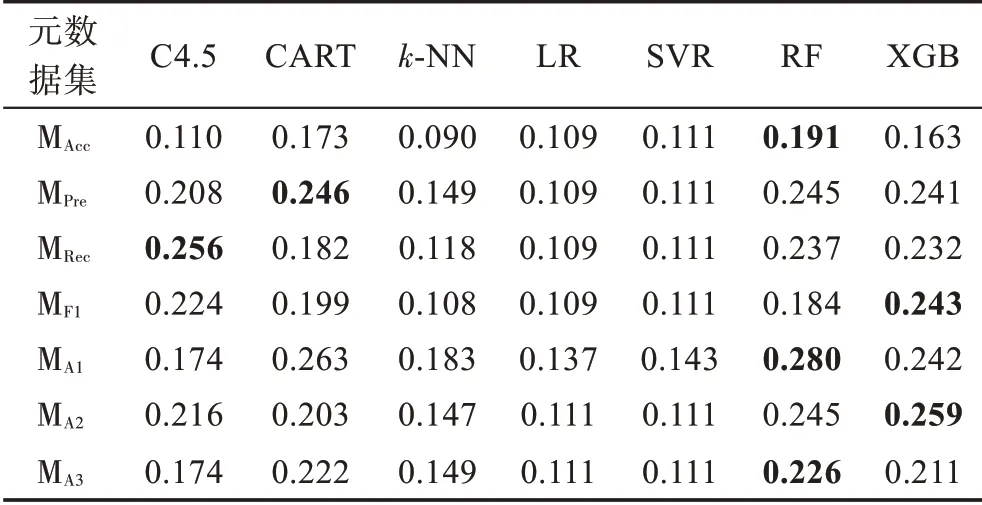
表12 元算法查全率指标值Table 12 Recall value of meta-learners
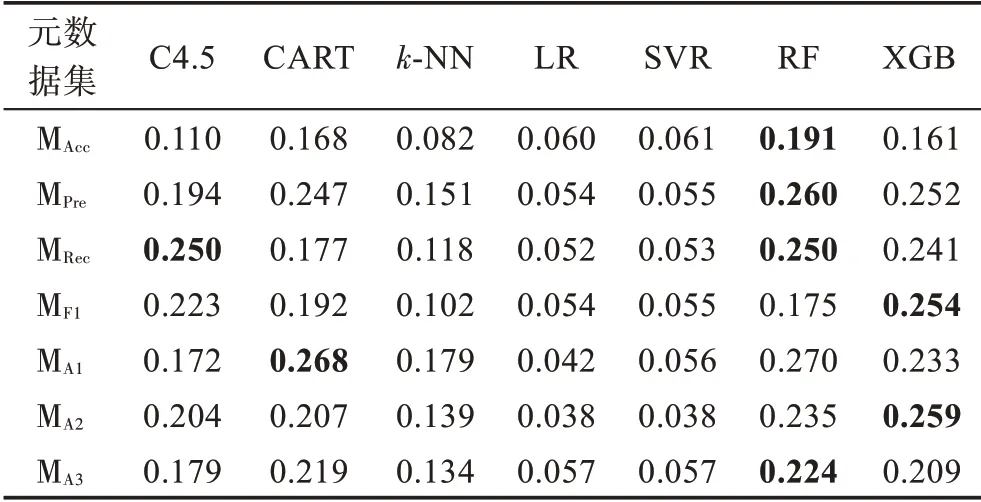
表13 元算法F1 得分指标值Table 13 F1 score value of meta-learners
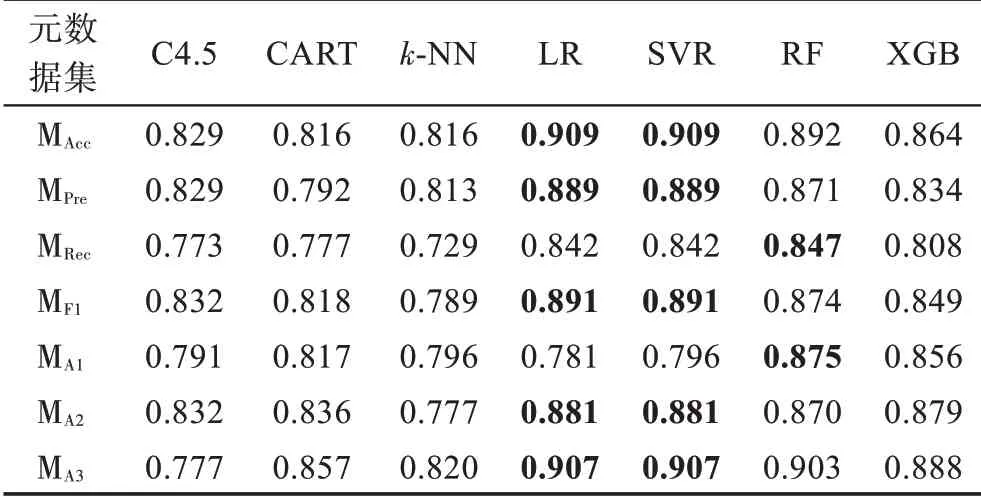
表14 元算法推荐准确率指标值Table 14 Recommendation accuracy value of meta-learners
观察表10~表14 可以发现,基于规则的C4.5 和CART 元算法在各元数据集上的性能表现相对平庸且稳定,两种元算法的整体性能较为接近,在不同元数据集和性能指标上各有优劣。基于距离的k-NN 元算法在各项指标上表现较差,难以在算法选择性能方面与其他元算法竞争。基于回归的LR 和SVR 元算法性能非常接近,两者在准确率指标上的性能较好,在查准率、查全率和F1 得分指标上的表现较差;另一方面,除MA1外,其在各元数据集上具备优越的推荐准确率性能。基于集成学习的RF和XGB元算法在不同元数据集的多个指标上可以取得最好结果,而两种元算法中RF更胜一筹,展现了一定的性能优势。
根据实验结果对元算法进行总结分析,基于规则的元算法整体表现较好,然而,该类元算法在各方面不具备突出优势,既在灵活性方面不如k-NN 元算法,又在算法选择性能方面不如基于集成学习的元算法。基于距离的k-NN 元算法整体表现较差,但其易于实现和调整、运行开销较小的特点,使其在对算法选择性能要求宽松但需要快速获得算法选择结果的应用场景中更有用武之地。基于回归的元算法可以产生与历史最优算法在性能上较接近的预测结果,但该方法生成多个回归元模型,具有较高的运行时间开销。此外,当回归元数据集中的性能指标值较为接近时,多个元模型的误差使该方法更容易将与最优算法性能指标值较为接近的其他候选算法预测为最优,因此,该方法难以适用于候选算法数较多或算法性能指标值差距较小的情况。基于集成学习的元算法整体表现出优异且稳定的算法选择性能,然而其运行开销较高。此外,直接使用常规的策略和参数设置难以充分利用集成的优势,该类型元算法仍有较大的性能提升空间。
5 问题与发展方向
基于元学习的方法经过多年发展,已经成为了解决算法选择问题的主要方法,相关研究成果也表明了这一方法在不同领域的适用性。然而,基于元学习的算法选择方法仍然存在许多亟待解决的问题,本章结合方法的关键内容和实际应用,探讨当前研究存在的挑战,阐述未来发展方向。
(1)元特征方面。随着不同类型元特征的提出和完善,元特征数量逐渐增加,元特征冗余现象也愈加突出。为了提高元算法性能,降低元模型训练和元特征提取的计算成本,可以研究计算开销更低且更能反映数据集特性的元特征,或者设计方法从已有的元特征中选择互补的元特征集合。
随着深度学习的快速发展,不同结构的数据都可以通过相应的向量嵌入方法映射为长度固定的向量,而将历史数据集转换为统一结构,通过向量嵌入方法提取元特征向量成为了元特征发展的一大趋势。
(2)元数据集方面。研究中,元数据集经常存在元实例数量较少或类不平衡的问题。对此,可以选择在来源领域、实例个数、属性类型和个数等方面互补的历史数据集,形成更多样化、数量更丰富的问题实例;应用数据增强方法亦可以扩大元数据集规模,使训练的元模型具备更强的泛化能力[67];最后,采用多种准则评估候选算法性能[88],降低综合性能较弱的候选算法选择概率,能够在一定程度上解决元数据集的类不平衡问题。
目前,多数研究关注于构建静态元数据集,即元数据集的内容固定不变,而根据已完成的算法选择结果,对元数据集进行反馈调整是研究方向之一。
(3)元算法方面。以算法集合为元目标构建多标签分类元数据集的研究较少,多标签分类算法和相关技术的应用是后续研究的一个重要研究点。此外,在部分应用场景中数据的获取较为困难,难以构建较大规模的元数据集,能够利用少量数据进行训练,充分发掘元特征与候选算法性能关系的元算法仍有待研究。
考虑到元特征的提取较为灵活,同时,元特征从不同角度描述数据集,具备一定互补性。设计集成学习方法,提取不同元特征构建元模型并进行组合,是提升算法选择方法整体泛化性能的可行方向。
(4)元模型性能指标方面。元模型的性能依赖于所选择的性能指标,如何根据元目标和元数据集特点选择合适的性能指标是必需考虑的问题之一。
研究中使用的指标忽略了错误预测的成本,对不同类型的预测错误设置不同成本权重,如合适算法被分类为不合适算法的错误成本更高,是元模型性能指标发展方向之一。
(5)动态算法选择方面。在实际应用场景中,针对流式数据的算法选择成为了基于元学习的算法选择方法发展趋势之一[89-90]。在此基础上,更进一步地根据资源需求和环境特点,动态地完成算法选择决策,是算法选择方法与实际应用需求相匹配的一个重要发展方向。
数据集的实例数量、类别数量、属性个数等特性易于获取且对数据集整体结构有着直观的表现。利用上述数据集信息,在算法选择过程中动态地为给定的候选算法提供指导性规则或偏好权重,是未来研究中的关注点之一。
