面向单调特征选择的改进模糊排序互信息

皮 洪，罗 川+，李天瑞，陈红梅

1.四川大学计算机学院，成都610065

2.西南交通大学计算机与人工智能学院，成都611756

从不同决策值之间是否存在有序结构的角度，可将分类问题分为有序分类及名义分类[1]。对于有序分类任务，不同决策值之间存在着有序关系。例如，学生的成绩可以分为5 个等级，分别是不合格、合格、中等、良好、优秀，在这5 个等级中存在有序关系，优秀表示最好的等级，而不合格则是最差的等级。当两个样本的条件特征值存在优劣关系，并且其决策特征值也存在对应的优劣关系，那么这两个样本之间存在单调约束。在有序分类的基础上，假设所有条件特征与决策特征之间都存在单调性依赖约束，那么该有序分类问题称为单调分类问题。单调分类任务广泛存在于信用评价、医疗诊断、风险评估等决策领域，具有重要的研究意义和实际应用价值。

特征选择是从原始特征中选择最具类别辨识性的特征以降低特征维度的数据处理过程[2-4]。近年来，面向单调分类任务的特征选择方法逐渐成为了人们关注的热点问题，并取得了一些研究成果。Hu等将最大决策边界准则引入到具有单调性约束的有序分类问题中，提出了基于ReliefF 和Simba 的单调特征选择算法[5]。Pan 等定义了特征的单调依赖度并提出了通过使用梯度下降最大化模糊偏好依赖的特征选择算法[6]。考虑到同时含有名义分类特征和单调分类特征的异构有序分类问题，Pan 和Hu 进一步定义了基于异构单调分类一致性的特征相关性度量函数，并利用基因算法对异构单调数据集中的最优特征子集进行求解[7]。Villela 等基于最大决策边界稀疏分类器，提出了一种基于容许有序搜索策略的包裹式有序特征选择算法[8]。

互信息作为信息论中一种常用的度量，通常用于评估两个随机变量之间的相关性。在名义分类任务中，已经提出了大量基于互信息的特征选择算法[2,9-13]。Qian 等针对不完备数据集提出了一种基于互信息的特征选择算法，并证明了互信息的单调性[2]。Kwak等提出了一种计算连续输入特征及离散输出类别间的互信息的方法，并将其应用到输入特征贪心选择算法中[11]。Battiti探讨了互信息准则在评估候选特征集的应用场景，并利用互信息准则来选择一组具有高度代表性的特征，将其作为神经网络分类器的输入数据[12]。Peng 等结合mRMR（minimal-redundancymaximal-relevance）及其他方法（如包装器）提出了一种两阶段的特征选择方法，能够以极低的代价选出一组具有高度代表性的特征[13]。为了将基于互信息的特征相关性度量准则引入到基于单调性约束的有序分类问题中，Hu 等定义了排序互信息（rank mutual information，RMI）及模糊排序互信息（fuzzy rank mutual information，FRMI），以评估单调分类任务中条件特征与决策特征之间的单调一致性，并基于这两种度量提出了面向单调分类的特征选择算法[1]。许行等在Hu 的算法的基础上，首先利用双向有序互信息生成不同的决策树，然后集成其分类规则得到最终的决策结果[14]。然而，实际应用中由于低质信息的存在，使得单调分类任务中往往存在决策不一致性。Hu 等所定义的基于RMI 及FRMI 的特征一致性度量准则在处理不一致单调分类任务时不满足特征集合与度量准则之间的单调性限制关系，进而影响特征重要性排序的启发式搜索过程。鉴于此，本文在Hu 等提出的RMI 和FRMI 的基础上提出了一种新颖的不一致单调分类中满足单调性限制关系的模糊排序条件熵以及模糊排序互信息，并将这种模糊排序互信息与最大相关最小冗余准则结合起来，实现了不一致单调分类任务的特征选择问题。在UCI 公开数据集上的仿真实验进一步验证了本文提出的特征选择算法具有更好的单调分类性能。

1 基本概念

本章介绍了单调有序分类、有序关系以及模糊排序互信息等相关基本概念。

1.1 单调有序分类

在粗糙集理论中，三元组DS=U,A,D是一个决策系统，其中U被称为论域，表示样本的非空有限集合；A表示条件特征的非空有限集；D表示决策特征集。令决策特征集为D={d1,d2,…,dk}，若任意di∈D是名义型特征，则U,A,D是一个名义分类决策系统。若决策特征满足关系d1＜d2＜…＜dk，则称U,A,D是一个有序分类决策系统。进一步，若样本的条件特征与决策特征之间存在单调约束关系，即对∀x∈U，v(x,A)≤v(x′,A) 有f(x)≤f(x′)，其中v(x,A)表示样本x在特征集A上的取值，f为决策函数。那么，就称U,A,D是一个单调分类决策系统。为了便于讨论，本文仅讨论有序关系增加的相关问题。

∀xi∈U，样本xi关于特征子集B的有序信息粒可表示为：

∀xi∈U，样本xi关于决策特征D的有序信息粒可表示为：

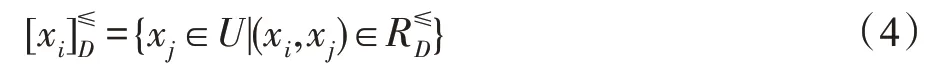
（1）当v(xi,a)＞v(xj,a)时，rij∈[0,0.5)；

（2）当v(xi,a)=v(xj,a)时，rij=0.5；

（3）当v(xi,a)＜v(xj,a)时，rij∈(0.5,1.0]。

使用Logsig Sigmoid 函数来计算样本xi和xj之间的有序隶属度rij：

样本xi的模糊有序集可表示为：

其中，rij能够反映样本xi劣于xj的程度[15]。

1.2 已存在的模糊排序互信息

为了处理单调分类决策系统中的特征选择问题，Hu 等[1]从信息论的角度定义了一种模糊排序条件熵和模糊排序互信息。

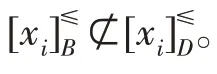
2 单调分类决策系统中的模糊排序互信息

本章将给出一种模糊排序互信息的定义，用于度量单调分类任务中的条件特征与决策特征间的单调一致性。这种新的定义能够克服单调分类任务不一致时模糊排序互信息不单调的缺点[16-17]。

为了定义新的模糊排序互信息，本文首先给出新的模糊排序熵及模糊条件排序熵的定义以及相关性质。

因此，模糊条件排序熵能够写为如下形式：

由上述讨论可以看出函数g(x,y)分别关于两个变量单调递增。

由上述两式可得g′≥0 且g′单增。

为了比较5种模型的具体预测精度，采用均方差(Mean Square Error， MSE)和决定系数(Determination Coefficient， R2)作为模型的评价指标。MSE是预测数据和原始数据对应点误差的平方和的均值，MSE越接近于0，代表数据预测结果越精确。R2是通过数据的变化来表示拟合结果的好坏，R2越接近于1，代表输入变量对输出变量的解释能力越强，对数据拟合的效果也越好。

这与已有条件矛盾，故假设不成立，即D完全依赖于B。

在给出上述定义及性质后，下面将定义新的模糊排序互信息。

3 特征选择的模糊排序互信息准则

本章首先讨论单调分类决策系统中模糊排序互信息用于特征选择的有效性，接下来介绍基于模糊排序互信息的特征选择算法。

3.1 模糊排序互信息的有效性

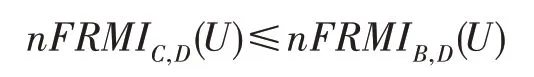
从定理4 中可以得出新定义的模糊排序互信息在一致单调分类决策系统中及不一致单调分类决策系统中均满足单调性。

3.2 基于模糊排序互信息的特征选择算法

上述章节提出了用于单调分类决策系统的基于模糊排序互信息的特征度量准则，接下来讨论基于该准则的特征选择算法。

在特征选择过程中，需要考虑两方面：所选特征间的冗余度要尽可能小以及所选特征与决策特征之间的相关性要尽可能大。从相关性及冗余度的角度来说，最优的m个特征是与分类最相关的特征。但是最优m个特征之间可能存在冗余，因此最相关的m个特征不一定比其他m个特征得到更好的分类准确率。因此，特征选择应该被分为两个过程：如何度量特征与决策特征之间的相关性以及如何处理特征间的冗余性。特征相关性可以利用本文定义的模糊排序互信息来度量。第二个问题可由下述定义4 解决，即采用最大相关最小冗余（mRMR）准则来选择当前第|B|+1个特征。

本文提出了一种两阶段的特征选择算法。第一个阶段根据特征评价函数对所有条件特征进行排序。将从候选特征集中选择最大化e(aj)的特征。被选择的特征与之前所选的特征冗余度小且与决策特征的相关性大。第一阶段的具体过程见算法1。在第二个阶段，利用算法2 选择出一个最具类别辨识性的特征子集。该特征子集具有最好的分类性能。

算法1模糊决策系统的特征排序

算法2选择最优特征子集的Wrapper算法

输出：最优特征子集B*。

1.将B分为如下子集：B1={ai1},B2={ai1,ai2},Bn={ai1,ai2,…,ain}

2.fork=1 tondo

3.从数据集DS中移除不包含在Bk中的特征，并将这个新得到的数据集记为DSk

4.在给定分类器下计算数据集DSk的分类性能

5.从所有数据子集中选出分类性能最好的数据集DSk0

6.令B*=Bk0

7.返回B*

4 实验分析

本章将通过实验验证所提方法的有效性及高效性。本文将第3 章提出的评价准则nFRMI与Hu 等提出的FRMI进行比较。

在接下来的实验部分，本文共使用两种单调分类器对所提方法的分类精度进行性能评测，分别是OLM（ordered learning model）[18]和OCC（ordinal class classifier），均在Weka 中得以实现。这两种分类器用于在Wrapper 阶段计算特征子集的分类性能，并由此选择出具有最优分类性能的特征子集。

本章的所有实验均采用10 折交叉验证法，将数据集分为10 份，轮流将其中9 份用作训练数据，剩余1 份用作测试数据。每次测试将得到对应的分类精度。10 次测试的结果平均值作为最终的算法评价指标。本文选取了4 组单调分类数据集进行性能实验，数据集详细信息如表1 所示。

表1 数据集描述Table 1 Description of datasets

表2 和表3 的数据描述了本文算法与对比算法在不同单调分类器作用下所得到的最优特征子集在10折交叉验证中的平均分类精度及标准差，每行中的最优分类精度用粗体表示。FRMI表示该列实验结果是基于Hu等所提出的度量函数的特征选择算法所得到的，nFRMI则表示实验结果是基于本文算法得到的。

表2 OLM 分类器下的分类精度比较Table 2 Comparison of classification accuracy by OLM 单位：%

表3 OCC 分类器下的分类精度比较Table 3 Comparison of classification accuracy by OCC 单位：%

从表2、表3 可以看出，分类器的选择会影响最终的分类精度。当选择分类器OLM 时，本文算法所得到的特征子集的分类精度在所有数据集上均优于原始数据集。与基于FRMI 的特征选择算法相比，基于nFRMI 的特征选择算法所得特征子集的分类精度在Crx、Ionosphere 及MachineCPU 三个数据集上是更优的，而在Pima 数据集上分类精度是相等的。当选择OCC 分类器时，基于nFRMI 的特征子集的分类精度在所有数据集上均优于原始数据集。与FRMI 相比，nFRMI 在Ionosphere、MachineCPU 及Pima 数据集上分类精度更优。

图1 和图2 分别展示了采用不同特征选择算法进行特征选择时，随着特征数量的增大基于OLM 和OCC 分类器的平均分类精度的变化趋势。从实验结果可以看出，除了OCC 分类器下的Crx 数据集，由基于nFRMI 的特征选择算法所得特征子集的分类精度优于或等于基于FRMI 的特征选择算法。另一方面，选用OLM 分类器的Ionosphere 数据集以及选用OCC分类器的MachineCPU 数据集，基于nFRMI 特征选择算法得到的特征子集在特征个数及分类精度两方面均优于基于FRMI 的特征选择算法。从数据集Ionosphere 可以看出，在特征选择的初始阶段，nFRMI的分类精度劣于原始数据集。随着特征选择的进行，nFRMI 的分类精度整体呈现上升趋势，直至优于原始数据集。从上述实验结果可得，基于nFRMI的特征选择算法在不同分类器、不同数据集下均能够提升分类精度并降低数据维度，且在大部分数据集下分类精度优于传统的基于FRMI的特征选择算法。这表明本文算法对于面向不一致性单调分类任务的特征降维问题是有效的。

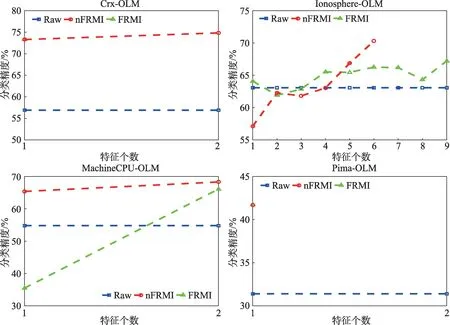
图1 OLM 分类器下所选特征的分类精度比较Fig.1 Comparison of classification accuracies with different number of selected features by OLM

图2 OCC 分类器下所选特征的分类精度比较Fig.2 Comparison of classification accuracies with different number of selected features by OCC

5 结束语

本文针对单调有序分类任务，提出了一种新颖的基于改进模糊排序互信息的特征选择算法，该算法能够有效克服已存在的模糊排序互信息在不一致性单调分类任务中不满足单调性约束的缺点。在特征选择过程中，使用最大相关最小冗余准则来确保所选特征之间的低冗余以及与决策特征之间的高相关性。实验部分，将本文算法与基于传统模糊排序互信息的特征选择算法在四个不一致性单调分类数据集上进行了对比实验，分析了两种算法得到的特征子集在两种单调分类器OLM 和OCC 下的分类精度性能比较。实验结果表明，与基于已存在模糊排序互信息的特征选择算法相比，本文算法在大部分数据集下能得到更优的分类精度，因此本文算法对于不一致性单调分类任务是有效的。

在后续工作中，将对本文所提出的改进模糊排序互信息在噪声数据干扰下的鲁棒性问题进行分析。并针对所提算法的计算效率问题进行优化，将其进一步扩展到面向动态单调分类的高效特征选择。