基于引信多维信息的防空导弹引战配合规律设计及仿真
2023-01-17施振兴苏怀维
贾 岛,王 楷,陈 磊,施振兴,苏怀维
(1.上海机电工程研究所,上海 201109;2.重庆红宇精密工业集团有限公司,重庆 402760)
防空导弹引战配合延迟时间用于在引信探测到目标启动后战斗部最佳炸点位置的调整,以保证导弹对目标的有效毁伤,满足武器系统对典型目标的单发杀伤概率指标要求[1]。目前,防空导弹引战配合延迟时间主要采用对相对速度进行插值,辅以根据目标类型、交会角等条件进行修正的方法[2]。由于引战配合延迟时间受相对速度、导弹及目标姿态、脱靶量、脱靶方位等诸多参数影响[3-4],无法用上述差值方法进行精确描述。若弹目交会末端相对速度、交会角、脱靶量等差异较大,现有方法很难同时兼顾,导致引战配合效率下降,甚至导致战斗部无法有效毁伤目标。
随着引信技术的发展,引信对弹目交会末端目标信息的测量手段越来越丰富,对交会末端目标信息的测量手段也越来越先进,由传统的仅具备侧向定角探测能力逐渐发展了倾角测量、方位角测量和弹目距离测量技术[5]。如何将这些测量信息用于引信启动后延迟时间的计算,形成能够兼顾全空域各类复杂交会条件的引战配合规律,成为引战系统设计的关键问题之一。
1 基于引信多维信息测量的引战配合模型
典型弹目交会条件如图1所示。
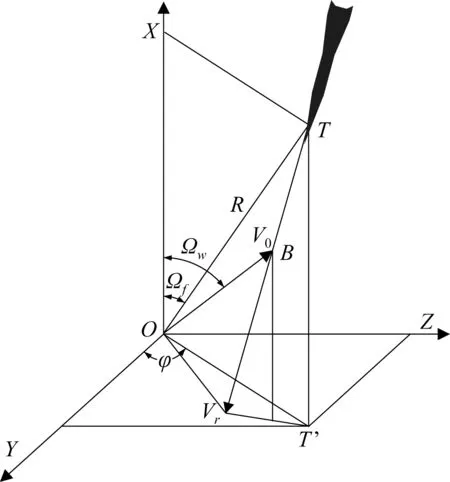
图1 典型弹目交会示意图Fig.1 Standard missile-target crossing
图1中,坐标系OXYZ为导弹弹体坐标系,某时刻目标位置为T,则
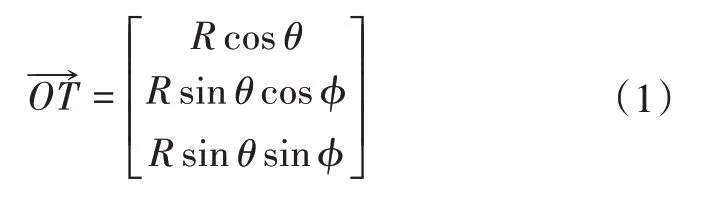
其中,R为引信启动时刻导弹与目标距离;Ωf为目标与弹轴夹角,对于侧向定角引信,Ωf为引信天线主波束倾角;φ为目标在OYZ方向的投影与Y轴的夹角。
根据“目标要害部位命中准则”,最佳炸点B应满足
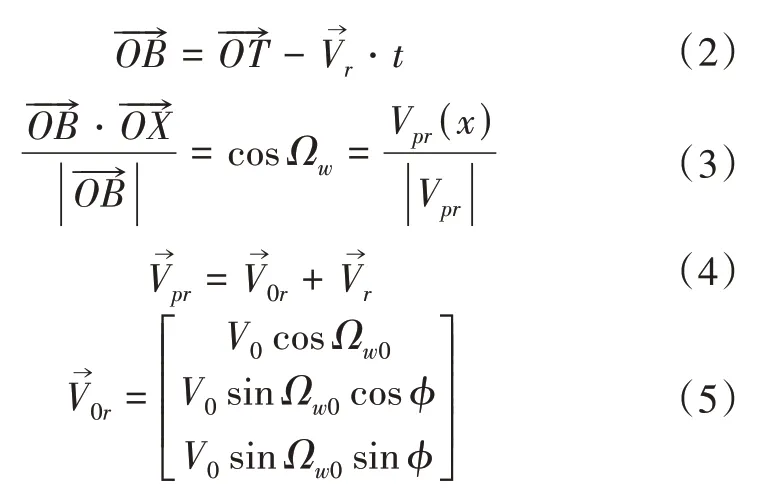
其中,Ωw为战斗部动态飞散方向角;Ωw0为战斗部静态飞散方向角;为弹目相对速度矢量;为破片动态飞散速度矢量;为破片静态飞散速度矢量;V0为破片静态飞散初速;为单位矢量。
由上述分析可知,决定引信最佳延迟时间t的因素包括两类:(1)引战系统自身的参数Ωf、V0和φw0;(2)弹目交会条件相关参数R、Vr、φ。
综上所述,对于给定的引战系统来说,系统本身的参数为不变量,延迟时间主要与弹目交会条件密切相关[6]。而上述交会条件参数中弹目相对速度Vr可由导弹制导系统测量信息(导弹和目标的速度、姿态等)解算得到,弹目距离R可利用引信线性调频测距技术或多普勒二维高分辨距离测量技术获取,目标方位角φ采用引信多路天线实时扫描比幅或比相技术获取。
考虑到该模型计算过程复杂,实际引信信号处理时间极短。直接将该模型嵌入导弹硬件计算平台内,在毫秒甚至微秒级时间内完成给定条件的延迟时间计算难度极大。因此,可考虑利用神经网络模型,利用式(2)通过大量的复杂交会条件仿真获取不同条件下最优延迟时间,作为学习样本,通过神经网络学习样本的模型特征[7-9]。将学习到的网络模型嵌入弹上计算平台,实现复杂条件下引战配合延迟时间的快速计算。
2 神经网络算法模型构建
建立神经网络模型时可利用弹目交会参数作为输入参数,以模型仿真计算的最优延迟时间作为输出参数。
考虑如下惯性坐标系XOY:原点O位于脱靶点处,X轴与弹目交会末端目标坐标系X轴方向一致,Y轴与弹目交会末端目标坐标系Y轴方向一致。在上述惯性系下,目标速度矢量简化为X方向速度大小。选取弹目交会末端导弹运动参数(速度大小vm,偏航角φm,俯仰角θm,滚动角γm,攻角αm,侧滑角βm)和目标运动参数(速度大小vt)和脱靶参数(R,φ)共9 个参数组成输入层。输出层为单一参数引战配合延迟时间t。选取4层隐含层,每层10个神经元节点。
其中,隐含层传输函数采用双曲正切函数(Tan-Sigmoid),即
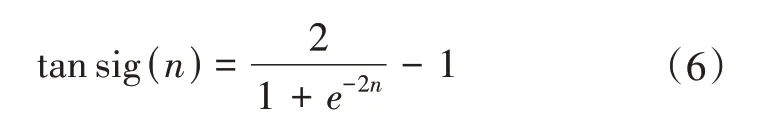
输出层传输函数采用线性传输函数。
神经网络计算训练过程如下:
(1)网络初始化。根据输入输出(X,Y)确定网络输入层节点数n、隐含层节点数l,输出层节点数m,初始化输入层、隐含层和输出层神经元之间的连接权值ωij,ωjk,初始化隐含层阈值a,输出层阈值b,给定学习速率和神经元激励函数。
(2)信息正向传递。神经网络输出计算如下:
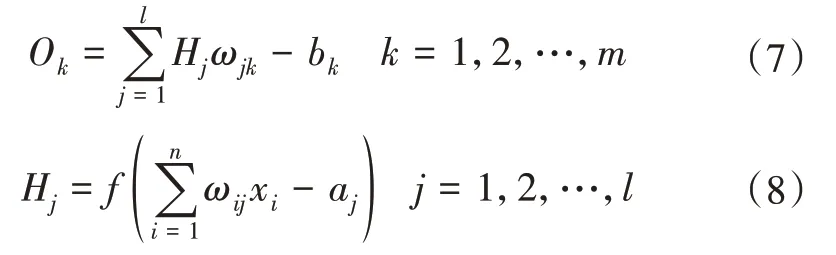
其中,f为隐含层激励函数。
(3)误差反向传播。计算过程如下:
其中,η为学习速率。
3 仿真分析与结果对比
随机生成4000 组弹目交会参数作为输入数据,并基于引信多维信息测量的引战配合模型,计算引战配合最佳延迟时间,作为对应输出数据。从输入输出数据中随机选取3800 组数据作为神经网络训练数据,200 组数据作为网络测试数据,并对数据进行归一化处理。
按该方法进行神经网络训练及验证,可利用遗传算法对网络中的权值和阈值进行寻优,适应度函数为预测输出和期望输出的误差绝对值之和。仿真结果如下。
3800 组训练样本与最佳延迟时间最大误差不超过0.4%(图2),验证样本下,经过训练后的神经网络预测结果与利用“最佳延迟时间”准则计算结果十分接近,平均误差仅为0.06%,最大误差为-1.59%。
利用传统插值方法计算得到的引战配合延迟时间与“最佳延迟时间”误差平均值为23%,最大误差为44.1%,如图3-5所示。
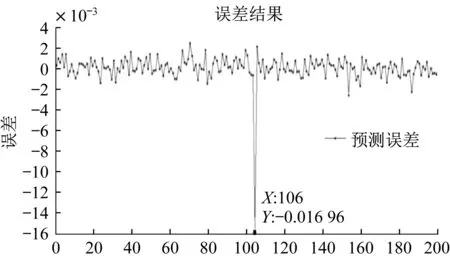
图4 验证样本预测误差Fig.4 Prediction error of validation data
利用某型防空导弹引战配合设计参数,分别采用上述2种引战配合延时规律,对验证样本的200条弹道进行了单发杀伤概率计算及引战配合仿真(表1)。结果表明,采用神经网络算法,防空导弹平均单发杀伤概率较传统插值算法提高了17.3%。

表1 不同算法导弹单发杀伤概率对比Tab.1 Comparison of killing probabilities of different methods for single missile
4 结 论
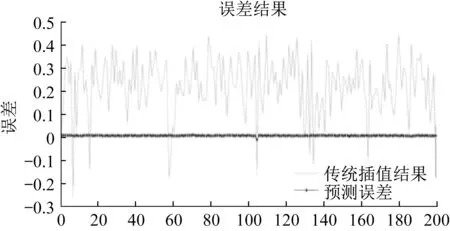
图5 验证样本预测误差与传统方法误差对比Fig.5 Comparison between the prediction error of validation data and that of the traditional method
利用神经网络算法,选择弹目交会末端导弹运动参数、目标运动参数和脱靶参数作为输出参数,对防空导弹引战配合最佳延迟时间样本进行训练,得到的模型能够很好地预测最佳引战配合延迟时间。该方法较传统引战配合延迟时间算法显著提高了对不同交会条件、脱靶条件的适应性,能够显著提高防空导弹单发杀伤概率。上述输出参数均能通过导弹飞行过程中雷达、惯导设备、导引头、引信等传感器测量获得,训练得到的神经网络算法简单,易于实施,可以应用在现有硬件条件的防空导弹中。
