基于改进遗传算法的路径规划问题应用

辛 钢, 宋少忠, 张 慧, 安 毅

(1. 吉林工商学院 工学院, 长春 130507； 2. 吉林工程技术师范学院 a. 数据科学与人工智能学院; b. 电气与信息工程学院, 长春 130052； 3. 长春汽车工业高等专科学校 信息技术学院, 长春 130013)

0 引 言

随着信息化赋能传统产业的迭代升级, 城市物流行业的信息化技术发展也越来越重要, 降低物流成本, 对多品类、 高频次的运输需求研究更有意义。评价程度较高的物流管理方法是指以合理的路线要求、 规范的运行时刻和较高的集载率保证每个汽车零部件供应商与总体装配中心的库存成本和运输成本双向降低, 其流程实现的复杂涌现程度和非线性较高。在传统的物流运输模式下, 多频次运输意味着车辆的集载率下降, 导致运输成本提高, 而循环取货物流模式高集载率的特性可在降低总体装配中心库存量的同时, 减少汽车零部件供应商本身的物流风险以及缺货甚至停线的风险, 从而降低综合物流成本, 整个模式由“推动式”取料转变为“拉动式”取料[1]。

近年来, 国内外诸多学者对路径规划方法进行了广泛研究。自然科学界的编码方法已经应用于智能化算法中, 如群体竞争优化算法[2]、 免疫算法[3]、 神经网络算法和模糊算法[4]等。启发式算法在路径寻优问题上起着重要作用, 其中蚁群算法易于与其他方法相互融合[5], 模拟退火算法无需考虑求解方向和初始状态[6], 自适应蚁群算法可解决易陷入局部最优和收敛速度等问题[7], 而基于改进遗传算法的高速公路交通拥堵状况的预测模型[8], 基于改进狼群算法的多机协同目标分配模型[9], 基于K-means的聚类模型和遗传算法的灾区救援路径规划[10], 很多模型都是以遗传算法为基础改进的。目前, 有学者将NSGA-Ⅲ(Non-dominated Sorting Genetic Algorithm, the Third Version)算法与势场蚁群算法进行融合设计在二维和三维栅格地图应用, 做无人机协同航迹规划[11]。不同于移动机器人和无人机在不同地形为了避障选择规划合适的路径[12], 制造业物流运输的路径规划需要考虑更多服务需求。传统的汽车零部件运输过程仅考虑在时间窗约束下或最优配送路线规划与匹配问题, 这造成了车辆集载率过度和容量浪费等问题, 导致物流运输成本没有达到最小化。针对此类资源浪费问题, 以实际需求出发, 按照合理高效的循环取货模式, 以Q城市汽车厂A从各供应商循环获取汽车零部件事件为例, 基于汽车厂A内实际需求作为出发点, 面对物流成本和运作效率的双重考验, 考虑循环取货过程中的零部件需求量、 供应商订单详情、 选配运输车辆容载率、 单车器具体积占比、 取送顺序、 厂区与供应商之间的时间需求等因素, 笔者提出遗传和大规模邻域搜索算法, 求解最优配送方案路径规划, 为有效落实高效循环取送货提供借鉴方案。

1 问题描述

基于汽车厂A产业需求和物流管理实际情况需要不断更新最优运输方案, 更新过程如图1所示, 汽车厂A循环取送货流程如图2所示。

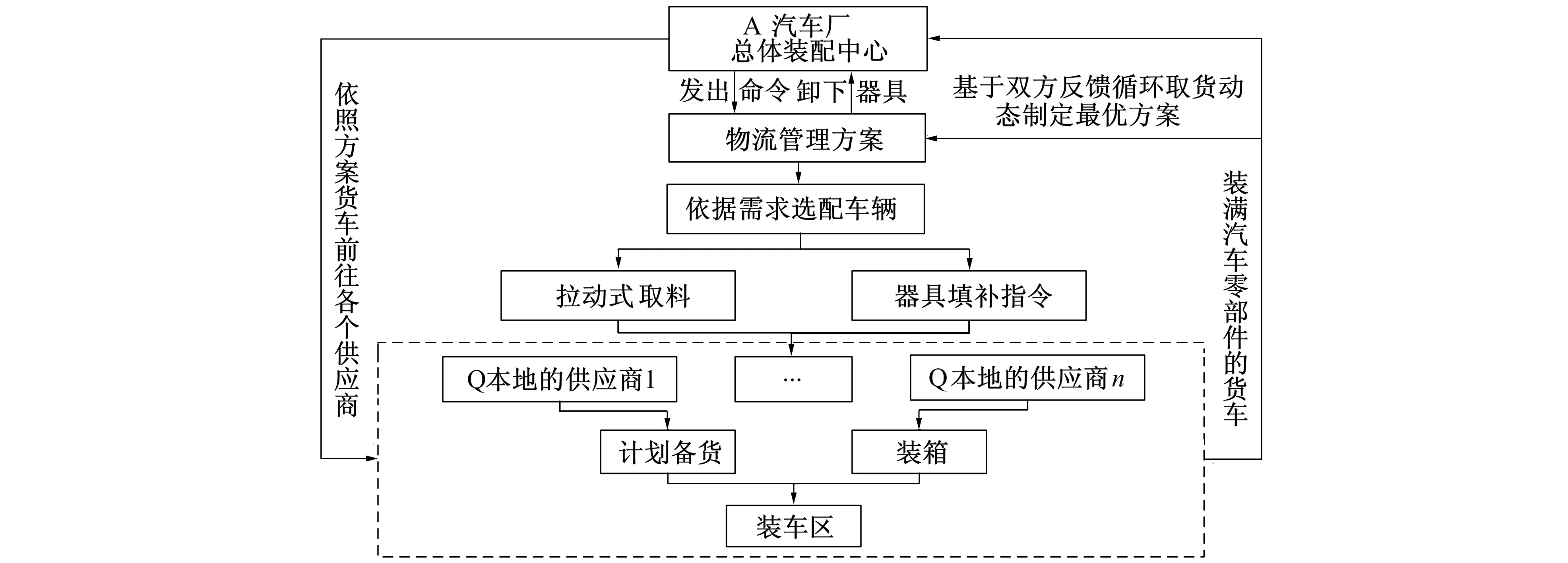
图2 A汽车厂循环取送货流程图Fig.2 Flow chart of automotive equipment manufacturer A’s milk-run

以Q地45个汽车零部件供应商为例, 按照计划对不同数量的汽车零部件提出需求, 即总体装配中心从供应商工厂取出货物, 由一个车队(包含不同车型)负责分别领取汽车零部件, 组织适当的行车路线, 目标是使汽车厂A的需求得到满足, 并能在一定约束下, 如厂A与供应商双方的时间窗、 选配车辆的容载率及利用率等条件, 达到诸如路程最优、 成本最小等目的。

2 基于遗传和大规模邻域搜索算法的设计

在现有文献中, 遗传算法作为将自然界的奥秘进行解码, 并应用于科学实践的典型。如基于多种群空间映射遗传算法的立体仓库储位优化问题[13], 在系统寻优上表现尤为突出, 旨在设计出一个能很好地解决车辆零部件运输问题的遗传算法, 为解决局部搜索能力弱的问题, 结合大规模邻域搜索算法LNS(Large Neighborhood Search)[14], 不仅将采用Solomon 数据集中的算例验证其正确性, 还会将其与普通的遗传算法进行对比, 最后基于汽车厂A的实际需求进行数值仿真验证其适用性。

利用遗传算法求解路径优化问题时, 不仅传承了染色体编码方式简洁性的特点, 又将大规模邻域搜索算法融入其中, 以此提高了算法的可靠性和高效性。其中, 用编码表达配送任务, 如123845967, 其中8和9代表总体装配中心汽车厂A, 并将汽车零部件供应商客户1234567划分为3段, 即划分为3条路径, 分别为0-1-2-3-0、0-4--5-0、0-6-7-0, 其中0代表总体装配中心汽车厂A, 这种处理方法便于统计当汽车零部件供应商数量固定且最大车辆使用数目也确定时的情况下, 以此作为遗传算法中染色体编码的具象表示, 进而更方便选取合适的适应度函数、 种群初始化、 选择操作、 交叉操作、 变异操作及大规模邻域搜索操作。

在适应度函数的处理上, 为确保解码的各条配送路径都满足载重量约束和时间窗约束, 笔者在求解过程中采用惩罚函数的方法解决违反约束问题, 具体计算如下

f(s)=c(s)+αq(s)+βw(s)

(1)

其中c(s)为选配车辆行驶的总距离,q(s)为违反各条路径车辆的容量约束之和,w(s)为违反所有供应商的时间窗约束之和。调节参数时, 根据违反约束条件的难易程度设定α与β的值。因容量限制为可控因素, 相比之下, 交通路况等信息对时间窗影响较为常见, 故将α设为10,β设为100。所有供应商违反的时间窗约束之和w(s)的计算如下

(2)

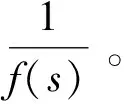
基于遗传和大规模邻域搜索算法中种群初始化至关重要, 构造初始解目的是降低遗传算法的搜索难度。过程如下：假设供应商数目为n, 一是从所有供应商中随机选择一个p； 二是初始化选配车辆使用数目q； 三是生成一个遍历所有供应商的序列Seq, 从随机选择的p供应商开始, 依次遍历至最后一个供应商n, 再从起始的供应商1开始继续遍历到p之前的所有剩余供应商; 最后, 遍历过程将生成初始解, 按照序列Seq进行遍历, 并将遍历到的供应商Seq(i)添加到k条路径中, 此时应分为第k条路径是否符合载重重量约束的两种情况： 1) 若符合, 则继续对插入位置进行考量, 包含当前路径为空时直接添加Seq(i)、 当前路径只有一个供应商时要根据左时间窗的大小添加Seq(i)以及当前路径有至少2个供应商时, 要遍历路径中连续的供应商的中间插入Seq(i), 按照Seq(i)的左时间窗是否在插入位置的前后供应商的左时间窗之间的原则, 决定Seq(i)当即插入还是将其放在当前路径的末尾处； 2) 若不符合, 则先使用目前选配的车辆, 对供应商Seq(i)之前的所有供应商进行访问, 然后再更新选配车辆数目。遍历过程中生成的这个初始解就是一个完整的配送方案, 将配送方案中的各条路径进行合并, 采用染色体编码方式, 将该种群转换为个体的过程就是种群的初始化过程。

这里采用轮盘赌选择方法, 按照适应度值的大小选择若干个适应度值大的个体进行后续的交叉、 变异以及大规模邻域搜索操作, 以染色体12345678编码为例, 后续过程如图3所示。值得提出的是, 交叉操作时先随机确定交叉位置, 然后将父代基因进行交换, 最后按照顺序原则, 剔除后出现的重复基因编码； 同样, 变异操作也要先随机确定变异基因的位置, 再进行变异基因的交换。

图3 生成新一代种群的过程示意图Fig.3 Schematic diagram of the process for generating a new generation of population

为保证求解质量, 将遗传算法与大规模邻域搜索算法(LNS)相结合, 其中LNS算法是交替使用destroy和repair两个方法逐步改善初始解的过程。将破坏和修复的思想融入物流规划中, 具体流程如下： 先使用破坏算子从当前解中移除若干个供应商, 再利用修复算子将被移除的供应商重新插回到破坏的解中。移除原则是基于相似性计算得到的若干个相似的供应商, 而插入原则是在满足重量约束和时间窗约束的前提下, 尽可能将移除的供应商插回到使车辆行驶总距离增加最少的位置上。

3 改进前后的算法运行结果对比分析

为验证笔者提出算法的正确性、 适用性与优越性, 将Solomon数据集中包含的rc205算例的23个随机点(包含一个总体装配中心)作为测试集算例。本测试仅选择了该数据集的一部分, 而原始数据集一共包含56个不同的算例, 每个算例包含多种信息, 包括供应商的坐标、 总体装配中心的货物需求量、 供应商的服务时间、 每个供应商的时间窗要求、 可选配车辆总数以及运输车辆的最大容载率等[15]。将遗传算法和提出的改进遗传算法求解目标函数的性能作为目标, 对前后两种算法求解目标函数进行了对比分析, 结果如表1所示。

表1 遗传算法与改进遗传算法的对比分析

图4 基于新提出算法的最优配送方案路线图Fig.4 Route map of optimal distribution scheme based on the new proposed algorithm

在试验过程中, 由于遗传算法收敛速度较慢, 而且收敛值也不理想, 大概在 360代开始收敛。而提出的改进遗传算法全局收敛性更强, 前期就能迅速收敛至最小值附近, 相比较而言, 收敛值更好, 大概在120代时开始收敛。笔者提出的改进遗传算法具体的最优配送方案路线如图4所示, 其最优配送方案路线如表2所示。

表2 最优配送方案路线表

4 数值仿真结果

针对带有左右时间窗容量受限的循环取货车辆路径优化问题, 为验证提出算法的有效性及优化过程中的收敛情况, 以Q市地图为例, 选取45个汽车零配件供应商和汽车厂A总体装配中心实际地址建立坐标系并进行算法仿真。各工厂相对距离和取送货的左右时间窗信息如表3所示, 其中“0”为起始点汽车厂A总装中心, 其坐标(10 km,10 km), 从“1”开始依次表示45个汽车零部件供应商, 汽车厂A选配车辆分别向Q市本地各个汽车零部件供应商按需循环取货。基于Q市实际路况, 以厂A为总装中心, 45个汽车零配件供应商与厂A的相对位置换算成坐标距离, 单位为km, 例如2号零部件供应商在厂A的西南方向, 西向2.1 km, 南向3.4 km处； 车辆对零部件供应商服务时间包括其进出供应商公司的时间和装载汽车零部件的时间, 设为30 min； 假设各个供应商公司汽车零配件包装箱大小相同, 根据选配车辆的大小不同, 普通车辆容载率设为100箱, 加长车辆容载率设为150箱； 选取厂A总装中心和所有供应商的左时间窗的最小值, 将其设为0, 其他时间窗以0为界, 以分钟为单位换算成每个供应商的左右时间窗, 例如已选取左时间窗1时00分为最小值, 2号供应商的服务时间是14时45分-15时30分, 则2号供应商的左时间窗为14时45分-1时00分=825 min, 右时间窗15时30分-1时00分=870 min。

仿真参数设置种群初始值随机, 优化收敛过程如图5所示, 仿真结果显示当迭代次数为第20代左右时, 最优值开始呈现收敛。当迭代次数为第100代时, 求出最优解, 其车辆使用数目为9辆, 车辆行驶总距离为207.803 4 km, 违反受限容量车辆数目为1辆, 违反约束左右时间窗车辆为3辆, 算法寻优时间为280.702 s, 具体的最优配送方案路线如图6所示, 最优配送方案路线如表4所示。

图5 优化收敛过程图 图6 最优配送方案路线图Fig.5 Optimization convergence process diagram Fig.6 Optimal distribution route map

表4 最优配送方案路线表

5 结 语

笔者提出了一种改进的遗传算法, 通过遗传和大规模邻域搜索算法相结合解决了以汽车厂A为实例的汽车零部件运输最优路径规划问题。首先, 将厂A与供应商之间的配送任务关系进行染色体编码。其次, 建立满足载重量约束和时间窗约束惩罚值的适应度函数。同时在遗传过程中, 利用破环算子移除供应商, 利用修复算子重新插入移除的供应商, 使总运输距离尽量小。基于相同测试集对改进前后的算法运行结果进行了对比分析, 对比结果显示提出的改进遗传算法在性能上具有显著的优越性。最后, 将算法的适用性和规划路线的收敛情况为出发点, 以Q市本地的45个供应商数据为例, 成功检验了算法在实际中的有效性和适用性。

参考文献：

[1]车路涛, 杨中华, 聂丞彬. 汽车零部件入厂物流优化问题研究现状与趋势 [J]. 物流科技, 2022, 45(2): 27-31.

CHE Lutao, YANG Zhonghua, NIE Chengbin. A Literature Review on Optimization of Inbound Logistics of Automobile Parts [J]. Logistics Technology, 2022, 45(2): 27-31.

[2]王晓丽, 贾东明. GCOA算法----一种新的智能优化算法 [J]. 价值工程, 2017, 36(22): 170-171.

WANG Xiaoli, JIA Dongming. GCOA Algorithm: A New Intelligent Optimization Algorithm [J]. Value Engineering, 2017, 36(22): 170-171.

[3]刘丽峰, 张树清, 李新红. 人工免疫算法路径规划在林火救援中的应用 [J]. 吉林大学学报(信息科学版), 2012, 30(4): 433-440.

LIU Lifeng, ZHANG Shuqing, LI Xinhong. Application of Artificial Immune Algorithm in Forest Fire Rescue Path Planning [J]. Jilin University (Information Science Edition), 2012, 30(4): 433-440.

[4]狄勇. 基于模糊神经网络和粒子群优化算法的机器人路径规划研究 [J]. 信息系统工程, 2018(6): 135-136,139.

DI Yong. Research on Robot Path Planning Based on Fuzzy Neural Network and Particle Swarm Optimization Algorithm [J]. China CIO News, 2018(6): 135-136,139.

[5]郑娟毅, 付姣姣, 程秀琦. 面向物流车辆路径规划的自适应蚁群算法 [J]. 计算机仿真, 2021, 38(4): 477-482.

ZHENG Juanyi, FU Jiaojiao, CHENG Xiuqi. Adaptive Ant Colony Algorithm for Logistics Vehicle Path Planning [J]. Computer Simulation, 2021, 38(4): 477-482.

[6]蒋丽, 王静, 梁昌勇, 等. 基于改进蚁群算法的众包配送路径研究 [J]. 计算机工程与应用, 2019, 55(8): 244-249.

JIANG Li, WANG Jing, LIANG Changyong, et al. Research on Crowdsourcing Distribution Path Based on Improved Ant Colony Algorithm [J]. Computer Engineering and Applications, 2019, 55(8): 244-249.

[7]张庆华, 吕小丹. 电商退换货车辆路径问题及蚁群算法研究 [J]. 计算机工程与应用, 2018, 54(22): 239-245.

ZHANG Qinghua, LÜ Xiaodan. Research on Vehicle Routing Problem with Return and Replacement in E-Commerce Environment and Its Solution to Ant Colony Algorithm [J]. Computer Engineering and Applications, 2018, 54(22): 239-245.

[8]黄承锋, 陈一铭, 李元龙. 基于改进GA算法的高速公路交通拥堵状况预测 [J]. 吉林大学学报(信息科学版), 2022, 40(2): 198-205.

HUANG Chengfeng, CHEN Yiming, LI Yuanlong. Highway Traffic Congestion Prediction Model Based on Improved Genetic Algorithm [J]. Journal of Jilin University(Information Science Edition), 2022, 40(2): 198-205.

[9]陈杰, 薛雅丽, 叶金泽. 基于改进狼群算法的多机协同目标分配研究 [J]. 吉林大学学报(信息科学版), 2022, 40(1): 20-29.

CHEN Jie, XUE Yali, YE Jinze.Research on Multi-Aircraft Cooperative Target Assignment Based on Improved Wolves Algorithm [J]. Journal of Jilin University (Information Science Edition), 2022, 40(1): 20-29.

[10]周小琳, 焦子恒, 胡锦林, 等. 基于智能算法的灾区救援路径规划 [J]. 吉林大学学报(信息科学版), 2020, 38(4): 516-521.

ZHOU Xiaolin, JIAO Ziheng, HU Jinlin, et al. Route Planning of Disaster Relief Based on Intelligent Algorithm [J]. Journal of Jilin University (Information Science Edition), 2020, 38(4): 516-521.

[11]袁梦顺, 陈谋, 吴庆宪. 基于NSGA-Ⅲ算法的多无人机协同航迹规划 [J]. 吉林大学学报(信息科学版), 2021, 39(3): 295-302.

YUAN Mengshun, CHEN Mou, WU Qingxian. Cooperative Path Planning for Multiple UAVs Based on NSGA-Ⅲ Algorithm [J]. Journal of Jilin University (Information Science Edition), 2021, 39(3): 295-302.

[12]李森杰, 郑洪瀛, 杨超, 等. 基于A*与DWA算法的混合路径规划算法研究 [J]. 吉林大学学报(信息科学版), 2022, 40(1): 132-141.

LI Senjie, ZHENG Hongying, YANG Chao, et al. Research on Hybrid Path Planning Algorithm Based on A*and DWA Algorithm [J]. Journal of Jilin University(Information Science Edition), 2022, 40(1): 132-141.

[13]隋振, 张天星, 吴涛, 等. 基于多种群空间映射遗传算法的立体仓库储位优化 [J]. 吉林大学学报(理学版), 2022, 60(1): 127-134.

SUI Zhen, ZHANG Tianxing, WU Tao, et al. Storage Optimization of Three-Dimensional Warehouse Based on Multi Population Space Mapping Genetic Algorithm [J]. Journal of Jilin University (Science Edition), 2022, 60(1): 127-134.

[14]南丽君, 陈彦如, 张宗成. 改进的自适应大规模邻域搜索算法求解动态需求的混合车辆路径问题 [J]. 计算机应用研究, 2021, 38(10): 2926-2934.

NAN Lijun, CHEN Yanru, ZHANG Zongcheng. Improved Adaptive Large Neighborhood Search Algorithm for Mixed Fleet Routing Problem of Dynamic Demands [J]. Application Research of Computers, 2021, 38(10): 2926-2934.

[15]凌海峰, 谷俊辉. 带软时间窗的多车场开放式车辆调度 [J]. 计算机工程与应用, 2017, 53(14): 232-239.

LING Haifeng, GU Junhui. Study on Multi-Depot Open Vehicle Routing Problem with Soft Time Windows [J]. Computer Engineering and Applications, 2017, 53(14): 232-239.