基于VMD-熵方法的管道信号特征提取方法

侯 男, 张 超, 路敬祎, 宋南南

(东北石油大学 a. 三亚海洋油气研究院, 海南 三亚 572025; b. 人工智能能源研究院; c. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318)

0 引 言

目前, 我国对油气等能源的需求量越来越多, 管道运输成为主要的能源输送工具之一。随着输气管道的总长度不断增加, 管线锈蚀、 施工以及人为破坏等因素造成的安全问题也日益引起人们重视。输气管道一旦出现泄漏, 将会给社会以及人类带来不可预估的危害[1]。因此, 对管道泄漏检测技术进行研究是十分必要的。

近年来, 国内外学者们已经提出了许多行之有效的管道泄漏监测技术, 如光纤法[2]、 声波法[3]和统计分析方法[4]等, 其中声波法具有灵敏度高、 误报率低、 实时性强的优点, 常应用于管道泄漏检测[5]。为此笔者基于声波法, 设计出一种具有较高准确率的输气管道泄漏检测特征提取方法。

目前, 针对管道信号的去噪预处理, 人们普遍采用非线性信号处理方法。采集的信号经变分模态分解(VMD： Variational Mode Decomposition)算法处理, 分解成多个本征模态函数(IMF： Intrinsic Mode Function), 每个IMF对应一个中心频率。文献[6-8]研究了VMD算法在管道泄漏检测中的应用, 并通过实验验证所提出的改进方法均是有效的。实验证明, VMD算法对信号的分解效果远超局域均值分解、 经验模态分解等方法, 具有一定的可行性与优越性。因此笔者以VMD算法为基础对管道信号进行去噪处理, 为后续的特征提取提供有效的数据集。

针对管道内随机复杂的声波信号, 人们使用熵值计算泄漏信号中产生新模式的概率大小, 并确定信号的复杂性。王超群[9]针对天然气管道缺陷检测, 采用能量熵对分解模态提取能量熵值, 并用其作为模糊C-均值聚类算法(FCM： FuzzyC-means Clustering Algorithm)的输入特征矩阵, 得出能量熵具有抗噪能力强, 稳定性好的结论。李传宪等[10]将峭度熵用于管道负压波信号泄漏检测特征提取中, 但该特征熵只能有效区分出切泵产生的负压波, 具有一定的局限性。刘炜等[11]将模糊熵和相似度结合用于对管道泄漏检测与定位, 证明该方法简单实用, 泄漏检测和定位可靠性强。

综上, 为使管道信号有效特征被准确提取, 笔者提出了基于VMD-熵方法的特征提取方法。从能量、 冲击特性和时间序列复杂度3个方面选取能量熵、 峭度熵和模糊熵作为特征参数, 首先将采集到的管道信号进行去噪处理； 然后计算去噪后管道信号的能量熵、 峭度熵和模糊熵, 将3个特征参数组成一组特征向量； 最后利用极限学习机(ELM： Extreme Learning Machine)对管道信号进行模式识别, 并通过实验证明了所提方法是可行的。

1 相关理论

1.1 能量熵

当运输管道出现异常状况时, 不同工况信号自身携带的能量存在差异。由于每个分量包含不同频段的信息, 当原始信号处于不同状态时, 信号在某些分量的能量分布就会发生变化。因此笔者从工况信号能量角度考虑, 利用能量熵对不同信号进行特征提取, 以达到提取信号有效信息的目的。能量熵的求解过程如下。

1) 计算每个有效IMF分量的能量

(1)

其中N为信号采样长度；xi为信号幅值。

2) 计算能量总和

(2)

其中m为有效分量个数。

3) 计算每个IMF分量的能量与总能量的比值和IMF分量的能量熵

pj=Ej/E

(3)

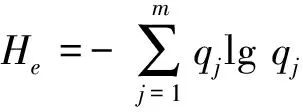
(4)

1.2 峭度熵

当输气管道发生异常时, 常出现包含明显冲击成分的工况信号。峭度可用于表征信号的冲击特性, 特别适用于轴承、 齿轮等机械的早期故障诊断, 但其属于时域特征中的无量纲量, 对信号不能进行准确的时频分析[12]。因此, 笔者基于峭度对冲击信号敏感的前提, 使用峭度熵对管道信号进行特征提取, 既保留了峭度的原始特性, 又从熵的角度考虑信号复杂性。计算过程如下。

1) 计算每个有效IMF分量的峭度

(5)

2) 计算峭度总和

(6)

其中m为有效分量个数。

3) 计算每个IMF分量的峭度与总峭度的比值和IMF分量的峭度熵

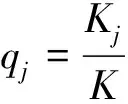
(7)

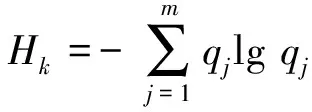
(8)

1.3 模糊熵

模糊熵是用于衡量时间序列复杂度的算法, 利用模糊隶属度函数计算两个向量的相似程度, 一定程度上可增强原始信号的抗干扰性能[13]。模糊熵的具体计算步骤如下[14]。

1) 假定数据长度为N的时间序列为{xi}={x1,x2,…,xN}, 对模式维数m初始化操作, 形成向量Xm(i), 如下

Xm(i)=[x(i),x(i+1),…,x(i+m-1)]-u(i)

(9)

(10)

其中Xm(i)为重构后的时间序列,i=1,2,…,N-m+1；u(i)为m个连续xi的均值。

2) 计算向量Xm(i)与Xm(j)之间的距离, 如下

(11)

其中i,j=1,2,…,N-m+1且i≠j。

3) 借助模糊隶属度函数定义向量Xm(i)和Xm(j)之间的相似程度, 如下

(12)

其中r为相似容限参数,r=Rδ, 其中R为常数,δ为数据的标准差。

4) 向量Xm(i)和Xm(j)之间的相似度定义为

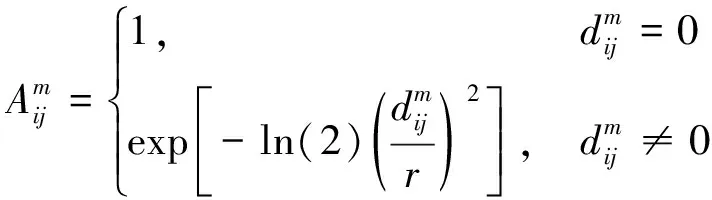
(13)

5) 定义函数

(14)

则可得m维度下的关系维度, 如下

(15)

6) 对m+1维向量重复步骤1)～5), 计算出m+1维度下数据的关系维度, 如下

(16)

7) 模糊熵的定义如下

FFuzzyEn(m,r,N)=lnΦm(r)-lnΦm+1(r)

(17)

根据文献[15]可知, 参数m、r、N设置值变化对模糊熵影响较小, 稳定性较好, 证明了模糊熵在抗噪性能方面的优势, 并且模糊熵值越大, 时间序列复杂度越高。因此, 笔者选用模糊熵作为管道特征提取参数, 在计算管道信号模糊熵时, 选择m=2,r=0.2。

1.4 极限学习机

2004年Huang等[16]提出一种基于单隐藏层前馈神经网络的监督型学习算法-极限学习机。ELM算法的网络结构由输入层, 隐含层以及输出层构成。用户输入的数据通过输入层传输到ELM中； 隐含层主要利用激励函数对信息进行变换； 输出层负责将转换后的数据向外部展示[17]。其网络基本结构如图1所示。

图1 ELM的基本结构Fig.1 The basic structure of ELM

由图1可看出, ELM属于一种多层神经网络, 每层级网络由多个神经元组成, 同一层级中的神经元彼此独立, 各层级之间前后连接, 每层的输出作为下一层的输入, 数据流动只有前向传递, 无反馈传播。其主要算法过程如下。

假定输入N个训练样本(xi,ti), 其中i=1,2,…,N,xi=(xi1,xi2,…,xin)T∈Rn,ti=(ti1,ti2,…,tim)T∈Rm,n为输入层节点个数,m为输出层节点数目。具有L个隐含层节点的标准单隐藏层前馈神经网络如下

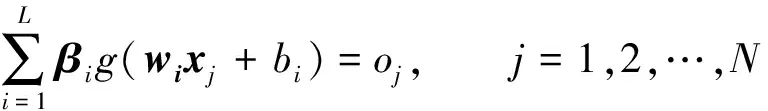
(18)

其中g(x)为激活函数, 第i个隐含层节点与输入层节点之间的输入权重为wi=(wi1,wi2,…,win)T,βi=(βi1,βi2,…,βim)T为第i个隐含层节点与输出层节点之间的输出权重,bi为第i个隐含层节点的偏置。

ELM训练模型的最终目标是使输出的误差逼近于零, 如下

(19)

将式(18)与式(19)联合简化如下

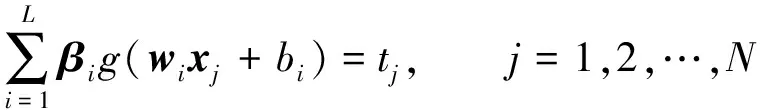
(20)

式(20)整理为用矩阵表示

Hβ=T

(21)

其中H为神经网络的隐含层输出矩阵,β为输出权重,T为期望输出矩阵。

(22)

(23)

最终求得

β=H+T

(24)

其中H+为矩阵H的穆尔-彭罗斯(Moore-Penrose)广义逆。

2 VMD-熵方法的特征提取方法

笔者对管道泄漏检测涉及的研究内容主要包括以下3个方面： 信号去噪、 特征提取和模式识别, 具体流程如下：

步骤1) 利用声波传感器采集多组管道正常、 泄漏和敲击信号；

图2 笔者方法流程图Fig.2 Flowchart of the method

步骤2) 对采集的管道工况信号进行去噪预处理；

步骤3) 提取不同工况下信号的能量熵、 峭度熵以及模糊熵, 通过多组管道信号拟合曲线观察特征提取效果；

步骤4) 将能量熵、 峭度熵以及模糊熵组合成一组特征向量输入到极限学习机中进行模式识别, 得到分类准确率结果。笔者方法流程如图2所示。

3 实验结果与分析

实验数据均来源于东北石油大学天然气管道泄漏检测模拟实验平台。管道总长为160 m, 管径为DN50, 管线上均匀分布15个泄漏点, 彼此间隔为10 m。实验平台利用压缩空气机为管道输送气体模拟天然气管道, 其中气体压力为0.5 MPa, 流量60 m3/h[18]。该平台的管道系统及控制台如图3a和图3b所示。采用LabVIEW编程环境采集正常、 泄漏和敲击3种工况信号, 采样频率为3 000 Hz。3种工况的采集方式如下： 正常信号为管道内气体正常输送的情况下采集的； 泄漏信号利用手动开关四分球阀阀门大小获取； 敲击信号是通过人为敲打管道外壁模拟的。管道泄漏检测实验平台采集得到的3种工况信号如图4所示, 可以看出, 管道工况的时域波形中含有较明显的噪声信号。

图3 管道泄漏检测模拟实验平台Fig.3 Simulation experimental platform of pipeline leakage detection

3.1 信号预处理

输气管道内的工况信号在传播过程中, 都会受到管道外仪器设备运行、 室外环境、 采集系统等影响产生一些随机噪声, 由于这些噪声都包含在采集到的数据中, 淹没一部分有效信号分量, 使泄漏检测的准确率降低[19]。因此, 为实现对管道泄漏信号有效特征的提取以及泄漏检测准确率的提高, 需要对采集的原始含噪管道信号进行去噪预处理, 使管道信号保留有效信号分量, 去除噪声分量。笔者采用张超等[20]提出的去噪方法, 利用混沌和sigmoid函数改进粒子群寻优搜索最优参数组[K,α], 输入VMD中进行信号分解, 并与欧氏距离结合去噪, 对图4中的工况信号进行去噪预处理, 得到去噪后的管道信号, 如图5所示。由图5可以看出, 3种管道工况信号已去除大部分毛刺, 且保留原始信号的基本形态, 为后续特征提取提供了有效数据集。

图4 3种原始含噪管道信号 图5 3种去噪管道信号Fig.4 Three kinds of original pipeline signals containing noise Fig.5 Three kinds of denoising pipeline signals

3.2 特征提取

为验证笔者选取特征参数的效果, 取3类工况信号样本各20组, 经去噪处理后, 得到管道信号如图5所示。由图5可看出, 管道不同工况信号波形波动的随机性和复杂度不同。因此笔者从能量、 冲击特性和时间序列复杂性3个角度选取能量熵、 峭度熵和模糊熵作为特征参数, 对不同工况信号进行分析。计算重构后信号的能量熵、 峭度熵和模糊熵, 得到的拟合曲线如图6所示。

图6 3种工况信号20组样本能量熵、 峭度熵和模糊熵拟合曲线Fig.6 Fitting curves of 20 groups of sample energy entropy, kurtosis entropy and fuzzy entropy for signals under three working conditions

由图6a可看出, 泄漏信号产生的能量熵值最小, 正常信号和敲击信号产生的能量熵与之相比较大, 但敲击信号和正常信号的能量熵值基本接近, 无明显区别。这说明, 能量熵虽可以描述泄漏信号特征, 但无法对其他两种信号有效提取, 若作为单一特征进行特征提取, 可能不够全面。

由图6b可知, 敲击信号产生的峭度熵最大, 泄漏信号和正常信号的峭度熵值相差不大, 有部分样本出现重合。因此, 峭度熵适用于敲击信号的工况识别, 对其他两种信号有较差的识别效果。

由图6c可知, 相比于能量熵和峭度熵只能较好地区分出一种工况信号, 模糊熵可以较好区分出3种信号, 正常信号的模糊熵最大, 敲击信号的模糊熵值处于中间, 而泄漏信号的模糊熵值最小。因此, 模糊熵可用于3种工况的分类识别。

3.3 ELM工况识别

图7 基于VMD-熵方法的ELM识别效果 Fig.7 ELM recognition effect based on VMD-entropy method

为验证笔者特征提取方法的分类识别效果, 将能量熵、 峭度熵和模糊熵构建成一组特征向量输入ELM中, 用于实现管道工况的模式识别。取3种类型的工况信号(正常信号、 泄漏信号和敲击信号)各100组, 得到300组样本集, 训练集与测试集比例为4 ∶1。首先利用240组管道数据样本对ELM原始模型进行训练, 得到训练好的ELM模型, 然后将60组测试样本输入训练好的ELM中进行模式识别, 得到测试样本识别分类准确率结果如图7所示。在图7中, 纵坐标表示测试集样本类别, 用纵坐标值1.0表示敲击信号, 用纵坐标值2.0表示泄漏信号, 用纵坐标值3.0表示正常信号。

由图7可看出, 在60个测试样本中, 仅在敲击样本中存在1个样本分类错误, 对泄漏和正常信号样本识别准确, 分类识别准确率达到98.33%, 说明笔者提出的基于VMD-熵方法经ELM识别具有较高的准确率。为验证笔者提出的特征提取方法的优越性, 将能量熵和峭度熵、 能量熵和模糊熵、 峭度熵和模糊熵、 峭度熵、 能量熵和模糊熵作为特征向量对3种工况进行ELM分类, 得到分类效果图如图8所示。由图8a可知, 将能量熵和峭度熵组成特征向量进行模式识别, 敲击信号存在5个分类错误, 正常信号存在1个分类错误, 虽然泄漏信号无分类错误, 但无法确定管道异常是由于敲击还是正常引起的。由图8b可看出, 利用能量熵和模糊熵组成特征向量进行ELM识别, 对敲击信号识别效果较差, 出现3个分类错误, 正常信号存在1个, 仍不能准确区分出管道异常情况。

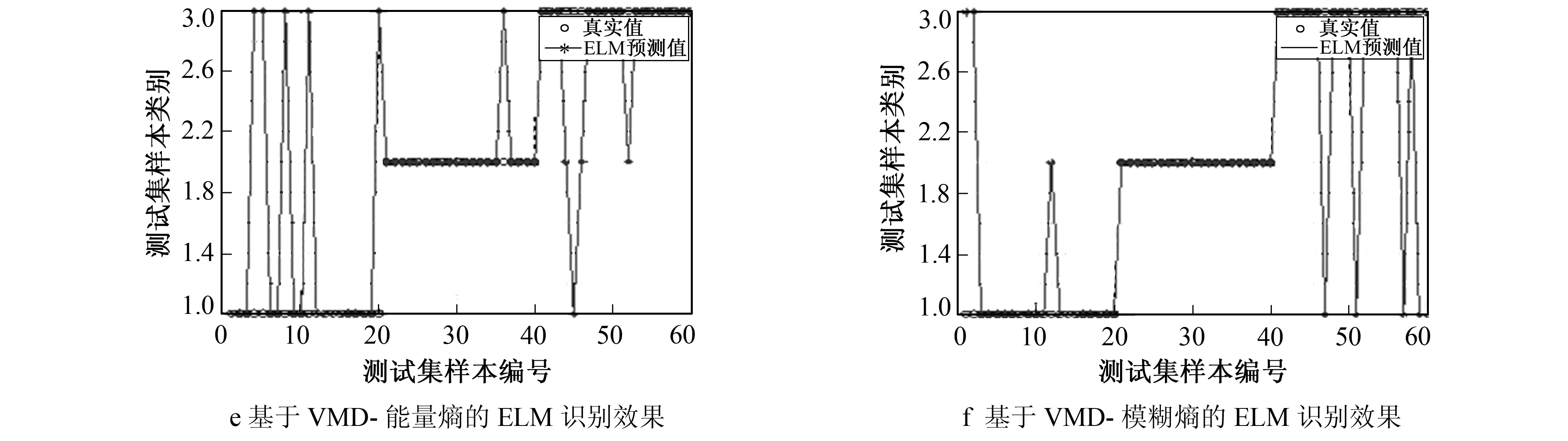
图8 基于各方法的ELM识别效果Fig.8 ELM recognition effect based on various methods

图8c是利用峭度熵和模糊熵进行识别, 可以看出敲击信号存在2个分类错误, 正常信号有3个, 不能判断出管道异常由何种情况引起。图8d把峭度熵作为单一特征参数进行识别, 敲击信号存在2个分类错误, 正常信号存在4个。图8e再把能量熵作为单一特征参数进行识别, 可以看出分类效果是最差的, 3种工况信号均存在错误。图8f是能量熵作为特征参数, 可以看出敲击信号存在3个分类错误(2个被分到了正常信号中, 1个分到了泄漏信号), 正常信号有5个, 分类效果较差。由此可知, 笔者所提特征提取方法具有明显优越性。

为使不同特征提取方法对管道信号分类效果对比更加直观, 将样本分类准确率进行整理得到表1。表1中的数值表示通过不同特征提取向量管道信号的240个训练样本正确分类的结果、 管道信号的60个测试样本正确分类的结果以及总准确率。

表1 不同方法ELM识别准确率

由表1可知, 基于能量熵、 峭度熵、 模糊熵组成的特征向量输入到ELM中准确率最高, 为98.33%； 而基于能量熵和峭度熵组成的特征向量输入到ELM中准确率较低, 为90%； 基于能量熵和模糊熵以及基于峭度熵和模糊熵分别组成的特征向量输入到ELM中, 虽然测试集的准确率相同均为91.67%, 但对训练样本分类识别基于峭度熵和模糊熵的特征向量效果较好； 单一熵作为特征的识别效果不如以上4种, 基于能量熵的识别准确率仅为83.33%, 基于模糊熵分类准确率稍高一些, 为86.67%, 基于峭度熵比前两者较好, 为88.33%。综上所述, 笔者提出的基于VMD-熵方法的特征提取经过ELM的分类识别, 无论是训练样本还是测试样本都达到了很高的准确率, 对管道不同工况信号有较好的识别效果。

4 结 语

在天然气管道泄漏检测过程中, 准确提取特征向量, 可以有效提高管道泄漏检测的准确性。因此, 笔者提出一种基于VMD-熵方法的管道信号特征提取方法。利用采集到的多组实际信号进行实验, 从不同角度选取能量熵、 峭度熵和模糊熵作为ELM的输入特征, 对不同特征提取方法的分类识别效果进行实验对比, 结果表明笔者所选特征参数组成的特征向量, 比基于能量熵和峭度熵、 基于能量熵和模糊熵、 基于峭度熵和模糊熵组成的特征向量以及单一熵作为特征参数的ELM工况识别准确率更高, 分类准确率达到98.33%。可见笔者选取的特征参数组合可以明显提高管道工况信号的分类精度, 证明了笔者方法的可行性与优越性。

参考文献：

[1]赵峰. 石油天然气长输管道的泄漏原因及检测方法研究 [J]. 石化技术, 2019, 26(10): 294-295.

ZHAO Feng. Study on Leakage Causes and Detection Methods of Long Distance Oil and Gas Pipeline [J]. Petrochemicals Technology, 2019, 26(10): 294-295.

[2]韩玲娟. 基于干涉型分布式光纤传感的天然气管道泄漏信号监测与识别 [D]. 杭州： 中国计量大学质量与安全工程学院, 2017.

HAN Lingjuan. Gas Pipeline Leakage Signal Monitoring and Recognition Based on Interferometric Distributed Fiber Optic Sensing [D]. Hangzhou: College of Quality and Safety Engineering, China Jiliang University, 2017.

[3]阚玲玲, 梁洪卫, 高丙坤, 等. 基于次声波的天然气管道泄漏检测系统设计 [J]. 化工自动化及仪表, 2011, 38(6): 653-655.

KAN Lingling, LIANG Hongwei, GAO Bingkun, et al. Design of Gas Pipeline Leak Detection System Based on Infrasonic Wave [J]. Control and Instruments in Chemical Industry, 2011, 38(6): 653-655.

[4]OVENS. Leak Detection in Pipelines by the Use of State and Parameter Estimation [D]. Disambiguation: Faculty of Information Technology and Electrical Engineering, Norwegian University of Science and Technology, 2014.

[5]刘翠伟, 敬华飞, 方丽萍, 等. 输气管道泄漏声波衰减模型的理论研究 [J]. 振动与冲击, 2018, 37(20): 109-114.

LIU Cuiwei, JING Huafei, FANG Liping, et al. Theoretical Study on Acoustic Attenuation Model of Gas Pipeline Leakage [J]. Journal of Vibration and Shock, 2018, 37(20): 109-114.

[6]LU J, YUE J, ZHU L, et al. An Improved Variational Mode Decomposition Method Based on the Optimization of Salp Swarm Algorithm Used for Denoising of Natural Gas Pipeline Leakage Signal [J]. Measurement, 2021, 185： 110107-1-110107-14.

[7]周怡娜, 路敬祎, 董宏丽, 等. 云相似度测量的变分模态分解去噪方法 [J]. 吉林大学学报(信息科学版), 2020, 38(1): 9-17.

ZHOU Yina, LU Jingyi, DONG Hongi, et al. Variational Mode Decomposition Denoising Method for Cloud Similarity Measurement [J]. Journal of Jilin University (Information Science Edition), 2020, 38(1): 9-17.

[8]杨丹迪, 路敬祎, 周怡娜, 等. 改进VMD算法在管道泄漏检测中的应用 [J]. 吉林大学学报(信息科学版), 2020, 38(4): 385-393.

YANG Dandi, LU Jingyi, ZHOU Yina, et al. Application of Improved VMD Algorithm in Pipeline Leakage Detection [J]. Journal of Jilin University (Information Science Edition), 2020, 38(4): 385-393.

[9]王超群. 应用CEEMD的天然气管道缺陷诊断方法研究 [D]. 北京： 中国石油大学(北京)机械与储运工程学院, 2020.

WANG Chaoqun. Research on Gas Pipeline Defect Diagnosis Method using CEEMD [D]. Beijing: College of Machinery and Storage and Transportation Engineering, China University of Petroleum (Beijing), 2020.

[10]李传宪, 逯雯雯, 石亚男, 等. 基于改进CEEMDAN-熵方法的管道泄漏工况识别 [J]. 石油化工高等学校学报, 2020, 33(1): 88-96.

LI Chuanxian, LU Wenwen, SHI Yanan, et al. Pipeline Leakage Condition Identification Based on Improved CEEMDAN-Entropy Method [J]. Journal of Petrochemical Universities, 2020, 33(1): 88-96.

[11]刘炜, 刘宏昭. 应用模糊熵和相似度的管道泄漏检测与定位 [J]. 机械科学与技术, 2016, 35(3): 437-443.

LIU Wei, LIU Hongzhao. Pipe Leakage Detection and Location Using Fuzzy Entropy and Similarity [J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(3): 437-443.

[12]刘鹭航, 张强, 王虹, 等. 基于峭度熵与分层极限学习机的动量轮轴承故障诊断研究 [J]. 中国空间科学技术, 2021, 41(3): 97-104.

LIU Luhang, ZHANG Qiang, WANG Hong, et al. Fault Diagnosis of Momentum Wheel Bearing Based on Kurtosis Entropy and Layered Extreme Learning Machine [J]. Chinese Space Science and Technology, 2021, 41(3): 97-104.

[13]刘新发. 基于EEMD多尺度模糊熵的S700K转辙机故障诊断的研究 [D]. 兰州： 兰州交通大学自动化与电气工程学院, 2020.

LIU Xinfa. Research on Fault Diagnosis of S700K Point Machine Based on EEMD Multi-Scale Fuzzy Entropy [D]. Lanzhou： School of Automation and Electrical Engineering, Lanzhou Jiaotong University, 2020.

[14]董国新. 基于ELMD多尺度模糊熵和概率神经网络的暂态电能质量识别 [D]. 秦皇岛： 燕山大学电气工程学院, 2016.

DONG Guoxin. Transient Power Quality Recognition Based on ELMD Multi-Scale Fuzzy Entropy and Probabilistic Neural Network [D]. Qinghuangdao： School of Electrical Engineering, Yanshan University, 2016.

[15]王磊, 纪国宜. 基于EMD模糊熵和SVM的转子系统故障诊断 [J]. 噪声与振动控制, 2012, 32(3): 171-176.

WANG Lei, JI Guoyi. Fault Diagnosis of Rotor System Based on EMD Fuzzy Entropy and SVM [J]. Noise and Vibration Control, 2012, 32(3): 171-176.

[16]HUANG G B, ZHU Q Y, SIEW C K. Extreme Learning Machine: A New Learning Scheme of Feed Forward Neural Networks [J]. Proceedings of International Joint Conference on Neural Networks, 2004, 2(2): 985-990.

[17]崔凯. 基于支持向量机和极限学习机的管道缺陷分类方法研究 [D]. 沈阳： 东北大学信息科学与工程学院, 2014.

CUI Kai. Research on Pipeline Defect Classification Method Based on Support Vector Machine and Extreme Learning Machine [D]. Shenyang: College of Information Science and Engineering, Northeastern University, 2014.

[18]梁洪卫. 油气管道泄漏声波信号检测与识别技术研究 [D]. 大庆： 东北石油大学电气信息工程学院, 2019.

LIANG Hongwei. A Study on Detection and Identification Technology of Oil and Gas Pipeline Leakage Acoustic Signal [D]. Daqing: School of Electrical & Information Engineering, Northeast University of Petroleum, 2019.

[19]周怡娜, 董宏丽, 张勇, 等. 基于VMD去噪和散布熵的管道信号特征提取方法 [J]. 吉林大学学报(工学版), 2022, 52(4): 959-969.

ZHOU Yina, DONG Hongli, ZHANG Yong, et al. Feature Extraction Method of Pipeline Signal Based on VMD Denoising and Dispersion Entropy [J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(4): 959-969.

[20]张超, 侯男, 路敬祎, 等. 改进的PSO-VMD算法及其在管道泄漏检测中的应用 [J]. 吉林大学学报(信息科学版), 2021, 39(1): 28-36.

ZHANG Chao, HOU Nan, LU Jingyi, et al.Improved PSO-VMD Algorithm and Its Application in Pipeline Leakage Detection [J]. Journal of Jilin University (Information Science Edition), 2021, 39(1): 28-36.