基于并行自注意力的石窟寺岩体裂隙发育研究
2023-01-17孙美君郭红桐张及鹏张景科
孙美君, 郭红桐, 王 征, 刘 洋, 张及鹏, 张景科, 李 黎
(1. 天津大学 智能与计算学部, 天津 300350; 2. 兰州大学 土木工程与力学学院, 兰州 730000;3. 中国文化遗产研究院, 北京 100029)
0 引 言
石窟寺大多开凿于砂岩沉积层上, 在自然因素和人为活动的影响下, 砂岩沉积层纵横裂隙发育, 加上砂岩遇水强度急剧下降等原因, 石窟寺发育出不同程度的裂隙病害[1], 主要表现为威胁岩体稳定性的卸荷裂隙和遇水渗漏的构造裂隙。在岩体本身结构力变化和雨水入渗等多种因素的共同作用下, 卸荷裂隙和构造裂隙会持续发育扩张, 极有可能导致岩体呈倾倒式、 滑移式、 断裂式破坏, 从而导致整个洞窟发生坍塌, 对文物本体造成不可挽回的损失, 甚至会危及管理人员及游客的生命安全。
除了人为活动和突发的重大气象灾害外, 从力学角度可将影响石窟寺岩体裂隙发育的原因分为岩体本身结构、 水和温度等[2-3]。其中岩体本身结构强度是影响岩体变形破坏的内在因素, 对岩体裂隙发育起主要控制作用。水则是最为重要的环境因素。岩土吸水后, 在岩体内部产生膨胀压力, 从而降低岩石强度。同时, 含结晶水盐类会聚集在岩土表面, 结晶时会产生压力, 从而加速岩体裂隙扩张破坏。此外, 温度也是影响岩体裂隙发育的重要因素。石窟寺大多处于西北地区, 昼夜、 季节温差等变化极大, 造成岩土体的交替性膨胀收缩, 从而在岩土体中产生温差应力, 进而影响岩体裂隙的发育。
石窟寺岩体裂隙发育预测问题的关键难点在于: 影响石窟寺岩体发育的因素存在多样化, 同时各项指标变化极其缓慢和微小。在这样的特殊环境下, 如何充分考虑岩体裂隙本身的结构性质并准确捕捉到多元因素间的非线性依赖关系, 进而构建解决石窟寺在不确定环境下的裂隙发育微变化预测问题的深度学习模型。而目前传统的机器学习方法在岩体裂隙发育的预测方面基本属于空白, 其他的统计学方法也难以对该问题进行建模, 并且在该领域国内外没有建立相关的数据集, 这也是岩体裂隙预测中的又一大难点。
笔者针对以上问题开展石窟寺岩体裂隙发育预测研究, 主要贡献如下。
1) 提出了一种新的基于深度学习方法的岩体裂隙发育预测网络模型, 即并行自注意力机制混合网络模型。该模型利用卷积与循环网络模块捕获时间相关性, 通过自注意力机制处理复杂的变量依赖关系, 有效提升了方法的准确性。
2) 创建了国内外首个该领域的数据集。将甘肃陇东地区规模最大的北石窟寺, 和四川省安岳石窟寺作为数据采集地点, 利用不同监测技术分别对石窟寺整体和岩体局部裂隙进行实时监测并保存数据, 最终形成一套完整的多元裂隙发育数据集。
1 相关工作
石窟寺岩体裂隙发育预测是时序数据预测领域的应用。自回归综合移动平均模型(ARIMA: Autoregressive Integrated Moving Average Model)[4]是典型的线性单变量时序数据预测模型。ARIMA的流行是由于其统计特性及模型选择过程中的Box-Jenkins方法。属于该类的还有其他自回归时间序列模型, 包括自回归模型(AR: Autoregressive Model)、 移动平均模型(MA: Moving Average Model)和自回归移动平均模型(ARMA: Auto-Regressive Moving Average Model)。然而, 这些自回归时间序列预测模型很难直接应用于多元数据的预测任务中, 因为对高维时序数据, ARIMA模型计算量太大, 不能很好地拓展到多变量时序数据。
另外, 向量自回归模型(VAR: Vector Autoregressive Model)[4-5]广泛用于多元时序数据预测, 它自然地将AR模型拓展到多变量时序数据。然而, 基于AR的模型和基于VAR的模型都无法捕捉到变量间的非线性依赖关系。因此, 为了对非线性进行建模, 使用了非线性模型的一些变体, 例如岭回归(RR:Ridge Regression)[6]、 线性支持向量回归(LSVR: Linear Support Vector Regression)[7]和高斯过程(GP: Gaussian Processes)[8]。但这些方法可对设定好的非线性关系进行建模, 却无法捕获多元时序数据的多种形式的非线性关系。
近年来, 深度神经网络由于其强大的捕捉非线性相互依赖关系的能力而受到极大关注。长短期记忆网络(LSTM: Long Short-Term Memory)[9]和门控循环单元(GRU: Gate Recurrent Unit)[10]作为递归神经网络(RNN: Recurrent Neural Network)的一种变体, 已在一些自然语言处理任务中取得优秀的成果, 同时也应用于多领域的多元时序数据预测任务, 如油田注水[11]、 功率预测等[12]。例如, 经常使用递归神经网络或其变体提供非线性时间序列预测。为实现更准确的预测, 最近学者们提出了更为复杂的网络框架结构, 如双自注意力网络(DSANet: Dual Self-Attention Network)[13], 利用全局时域卷积和局部时域卷积, 以捕获全局和局部时域模式的复杂混合。但对石窟寺岩体裂隙短期预测任务, 由于石窟寺岩体裂隙变化周期十分漫长, 短期预测也需要相对长期的数据信息, 需要对长期的更为复杂的依赖模式进行建模。然而, DSANet可能对相对长期的信息不敏感, 不能完全捕获时序数据特征。另外, 自注意力机制(Self-Attention)[14]在自然语言处理任务中展现出强大的性能, 它可以捕获句子中单词的句法特征, 同时可以更容易地捕获长距离的相互依赖特征。但Self-Attention的计算需要二次计算时间复杂度, 而且Self-Attention的操作会使模型复杂度较高, 并且对长输入, 具有较高的内存使用率, 因此文献[15-16]都采用改进方法降低自我注意机制的计算复杂度。在DSANet中, 将自注意力网络应用于时序数据预测任务, 用于捕捉多元时序数据中不同序列之间的依赖关系。
综上所述, 基于统计学的时序数据预测方法和现有的深度学习方法不适用于本文中的应用场景, 不能准确捕捉时间步长和不同单变量序列中的复杂依赖关系, 因而不能对石窟寺岩体裂隙发育进行建模。
2 基于深度学习的岩体裂隙发育预测
2.1 问题定义
石窟寺岩体裂隙发育预测是典型的多变量时序数据预测问题。裂隙宽度的发育不仅取决于岩体裂隙宽度的历史数据, 还取决于多种外界环境影响因素数据, 这些数据间潜在的相关性对预测岩体裂隙未来值至关重要。
2.2 网络结构
笔者提出了一种新的基于深度学习方法的时间序列网络模型FDPNet, 模型架构如图1所示。首先利用并行网络充分发挥局部卷积模块和全局循环模块在解决时间序列问题方面的优势, 对多元时间序列中的每个单变量序列提取时间特征, 构建具有不同时间尺度的时间模式表示向量; 之后自注意力模块利用稀疏自注意力机制对不同单变量序列进行建模, 捕捉不同时间序列之间的依赖关系; 最后将自注意力网络模型输出与自回归模型输出进行求和, 得到最终的预测结果。
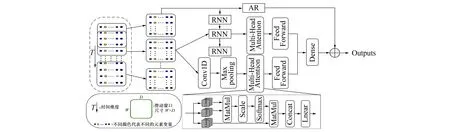
图1 FDPNet模型架构图Fig.1 Architecture of FDPNet
2.2.1 全局循环模块
当前预测时刻的数值与时间窗口中不同时间步长的数值存在多种依赖关系, 因此要考虑时间窗口中不同的时间模式。对多元时序数据预测问题, 经常使用RNN捕捉时间模式, 然而由于梯度消失的影响, 其难以对长时间序列进行建模。因此选用RNN的变体LSTM, 它解决了梯度反传过程中由于梯度逐步缩减而产生的梯度消失问题。具体到时序数据任务中, 其非常适合用于处理时间序列高度相关的问题, 尤其是复杂的长序列问题, 这是卷积神经网络(CNN: Convolutional Neural Networks)无法媲美的。
对单变量时间序列{x1,x2,…,xT}, 其中xi∈n, LSTM会定义递归函数F, 并在其中引入记忆单元, 因此其可更好地解决长期依赖问题。LSTM计算每个时刻t的隐藏层状态ht,ct定义如下
ht,ct=F(ht-1,ct-1,xt)
(1)
其由
定义。其中it,ft,ot和ct∈m,Wxi,Wxf,Wxo和Wxg∈m×n, sigmoid为激活函数, ⊙为按元素相乘。
全局循环模块用于提取单变量时间序列的所有时间步长的时域模式, 通过对不同单变量序列进行特征提取, 最终得到时间模式表示矩阵, 矩阵中的每列可看作是一个单变量序列的时间表示。
2.2.2 局部卷积模块
考虑到与预测时刻相对距离更近的时间步长对预测准确性的影响更大, 笔者还采用了并行于全局循环模块的局部卷积模块, 用于捕捉短期时间模式。相比于长期时间模式, 短期时间模式对时间序列预测更有帮助。

2.2.3 自注意力模块
对多元时序数据预测, 笔者试图利用历史数据预测未来值。但不可忽略的是, 多元时序数据中的不同序列之间可能存在复杂的动态依赖关系。因此, 为提升模型预测能力必须要准确捕捉不同时间序列之间的相互依赖性。在文中加入自注意力模块, 其由稀疏自注意力层和前馈网络层组成。
通常传统的自注意力机制输入形式是元组输入(Query,Key,Value), 然后进行缩放点积, 可表示为
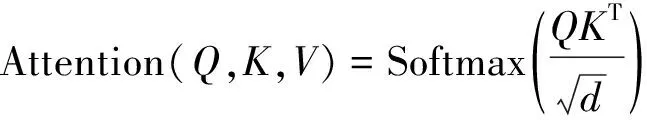
(7)
其中Q∈LQ×d,K∈LK×d,V∈LV×d, Softmax为激活函数,d为输入数据的维数。为进一步研究自注意力机制原理, 设定qi,ki,vi分别代表Q,K,V的第i行, 则第i个Query的注意力稀疏的概率公式定义为
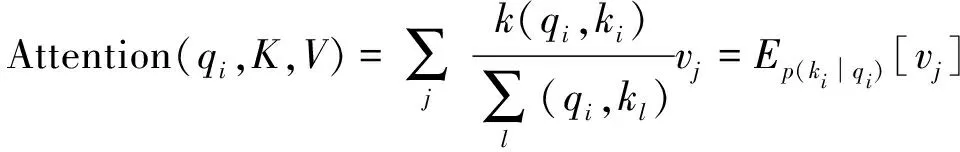
(8)

根据研究发现, 自注意力机制的概率分布存在潜在的稀疏性。为度量Query的稀疏性, 由Zhou等[16]研究得知, 可使用KL(Kullback-Leibler)散度。因此可得到稀疏注意力机制的公式为

(9)
前馈网络层由两个线性变换层组成, 稀疏自注意力机制的输出结果经过前馈网络层, 得到最终的输出。
2.2.4 自回归模块

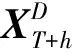

(10)
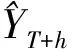
3 实 验
3.1 数据集
将甘肃陇东地区规模最大的北石窟寺和四川省的安岳石窟寺作为数据采集地点, 对石窟寺整个区域、 石窟寺洞窟和岩体裂隙进行数据监测。在石窟寺整个区域利用综合气象站、 无人机遥感、 全球导航卫星系统位移监测等监测技术进行区域定位, 观测区域位移变化和气象状况。在石窟寺洞窟中, 布设温湿度监测装置和智能激光断面扫描设备, 充分监测岩体裂隙局部发育变化。

图2 裂隙宽度数据采集环境Fig.2 Fissure data collection environment
笔者的数据集从2020年10月21日开始采集, 截止2021年12月10日, 数据集中含有温度、 湿度、 霜点等外部环境数据以及裂隙宽度、 岩体震动幅度数据等。裂隙宽度数据采集频率为2 h一次, 温湿度等环境信息数据采集频率为20 min一次, 岩体震动数据采集频率为1 s一次。不同采样频率的数据经过预处理操作, 最终形成一套完备的石窟寺岩体裂隙监测数据集GTMD (Grotto Temple Rock Mass Monitoring Dataset)。数据集详细信息如表1所示, 各元素采集频率均为2 h一次。

表1 数据集详细信息
通常传感器采集的数据往往会引入噪声且存在数据不平滑的现象, 同时由于外界环境数据与裂隙宽度数据的采样频率不同, 使原始数据不能直接用于模型输入。基于此, 对数据集进行了预处理, 首先对采集的数据进行标准化操作, 使采样频率高的数据向采样频率低的数据对齐, 并在同一段时间区间内, 针对采集时间间隔短的外部环境变量数据进行分时段取值使其与裂隙宽度数据, 在时间上对准于同一时刻, 最终结果是统一数据元素的数量级为2 h; 此外使用奇异谱分析(SSA: Singular Spectrum Analysis)算法对数据进行去噪, 之后对数据集进行卷积平滑。经过数据预处理操作, 构建了完整的多元时序数据集, 可直接用于模型输入, 使模型预测结果更为精准。
实验中, 预处理后的数据集按照时间顺序分为训练集(60%)、 验证集(20%)、 测试集(20%)。
3.2 实验细节及评价指标
实验基于Python 3.5环境, 使用深度学习框架Pytorch 1.2和机器学习库Scikit-learn实现笔者模型和基准模型。硬件环境配置为Intel E5, 24核48线程, 显卡为NVIDIA RTX2080Ti。
为评估FDPNet的有效性, 使用常见的算法作为基准模型在相同度量指标下对其进行对比, 基准模型如下:
1) AR: 线性自回归模型[4];
2) LSVR: 具有支持向量回归目标函数的向量自回归模型[17];
3) CNN: 含有卷积层和池化层的卷积神经网络[18];
4) LSTM: 长短期记忆网络[9];
5) DSANet: 自双向注意力网络模型[13]。
在实验过程中, 对所有方法可调参数进行网格搜索, 对超参数进行优化, 通过优化超参数之间的最优组合改善模型性能。对笔者网络模型, 预测窗口大小范围是{3,6,12,24}, 这表明单次预测窗口设置为6~48 h。网络模型中局部卷积模块中的卷积核长度从{3,6,12}中选择。笔者使用Adam优化器更新梯度, 并且设置学习率为0.01。
在GTMD数据集上, 笔者提出的模型与其他相关模型进行了比较, 为衡量多变量时间序列预测的各种方法的有效性, 实验遵循相同的评价指标: 均方根误差(RMSE: Root Mean Square Error)、 平均绝对误差(MAE: Mean Absolute Error)。评价指标分别定义为
1) 均方根误差(RMSE)
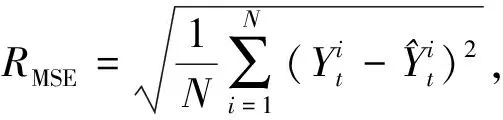
(11)
2) 平均绝对误差(MAE)
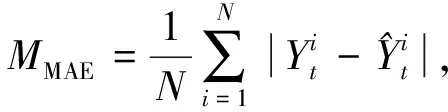
(12)

3.3 结果分析
笔者总结了大量实验结果对基准模型和FDPNet的时序数据预测性能进行分析。表2给出了基准模型和FDPNet在GTMD数据集上的多元时序数据预测实验结果和不同模型评价指标的比较分析。模型实验结果如图3所示。
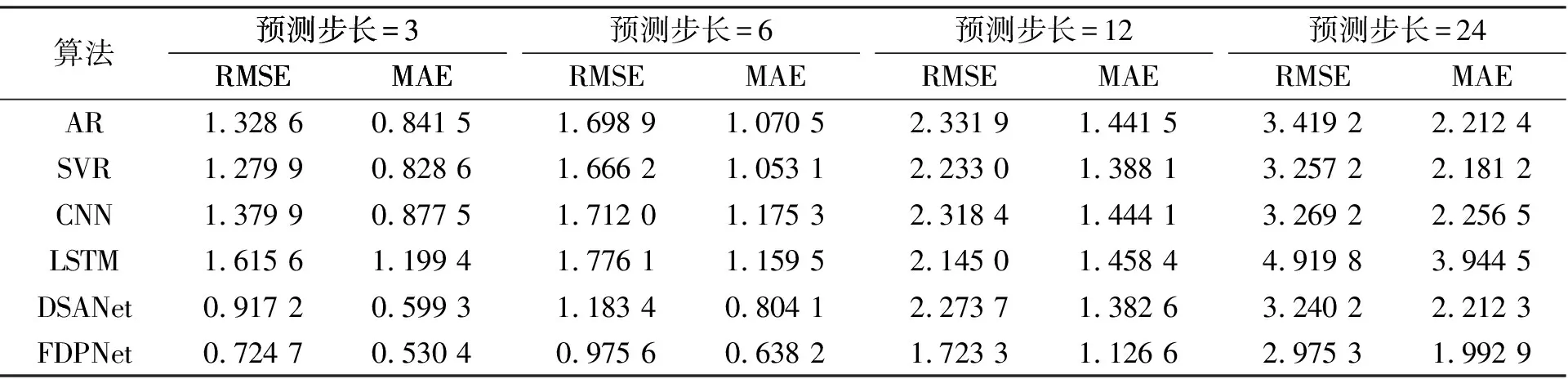
表2 不同算法模型在石窟寺岩体数据集上的实验结果
如表2所示, 实验结果表明, 笔者模型在不同时间步长上都具有最优的预测性能, 并且与单一的深度学习模型和线性自回归模型相比, FDPNet显著提高了预测精度。另外, 笔者通过实验发现了一个普遍现象, 当预测时间步长增加时, 所有模型的数据预测能力逐渐下降, 这说明在进行多步迭代预测时, 预测误差在不断增加, 这也反映了时序数据预测的一个实际问题, 即预测的时间步长越长, 预测难度越大。根据实验结果还可以看出, 与基准方法相比, FDPNet在短期预测时能保持最低的预测误差, 这说明FDPNet完全可以捕捉不同时间步长与多个时间数据序列中的依赖关系。
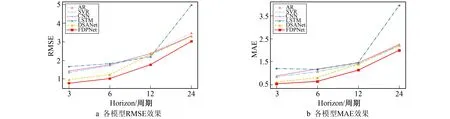
图3 模型实验结果折线图Fig.3 Model experiment results
众所周知, 时间窗口的大小会对模型预测性能产生影响。为选择最佳的时间窗口大小, 利用基准模型DSANet和笔者模型进行参数敏感度实验, 实验结果如表3所示。当时间窗口大小w=36时, FDPNet在时间窗口参数范围内具有最小的预测误差, 基准模型预测性能也基本优于其他时间窗口大小。因此, 可得出结论: 在该时间窗口中已经包含了所有对预测未来值有用的特征, 它是最优的时间窗口大小。

表3 时间窗口大小w敏感度实验
3.4 消融实验
为验证FDPNet设计的有效性, 进行了详细的消融研究。因此对笔者模型框架中每次移除一个模块, 将移除模块的基准模型命名如下。
1) w/oGL: 网络框架中移除全局循环模块。
2) w/oLC: 网络框架中移除局部卷积模块。
3) w/oAR: 网络框架中移除AR模块。
消融实验使用RMSE和MAE作为评价指标, 实验结果如图4所示。实验结果表明, 笔者网络框架在不同预测步长的情况下都得到最优的预测结果。
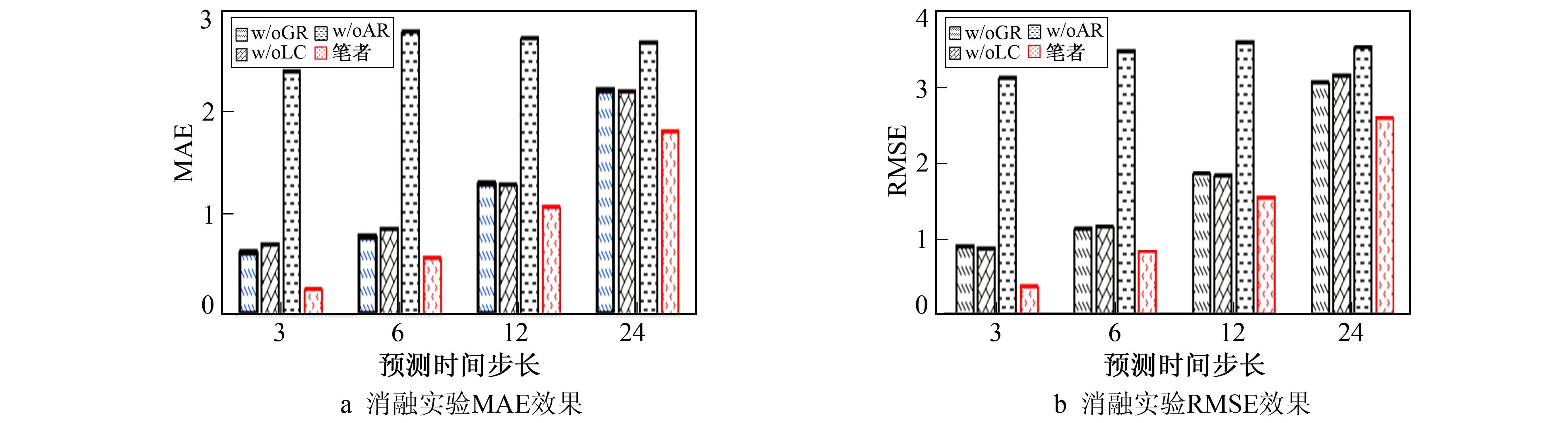
图4 消融实验结果Fig.4 Ablation experiment results
图4结果表明, 设计良好的模型结构会使模型更具鲁棒性和有效性。在框架中移除AR模块后, 模型数据预测性能大幅度下降, 说明AR模块在本数据集上进行数据预测时具有至关重要的作用。w/oGL和w/oLC两种模型出现预测性能小幅度下降的现象, 这说明单分支模型可以捕获大部分特征, w/oLC可以充分提取短期时间模式特征, 但却丢失相对长期的特征, 从而导致预测性能下降。消融实验充分证明, 框架中的所有模块是不可缺少的。
4 结 语
针对石窟寺关键岩体裂隙发育预测任务, 笔者提出了一种新颖的深度学习网络框架FDPNet。通过将局部卷积模块、 全局循环模块与强大的自注意力网络相结合, 充分捕获不同时间步长与不同时间序列之间复杂的非线性相互依赖关系。同时加入自回归模型, 使线性模型和非线性神经网络模型相结合, 显著提高了多元时序数据的预测准确率。笔者着重于对石窟寺岩体发育进行短期预测, 在GTMD数据集上可以实现较好的预测结果。而对于石窟寺岩体, 周期是漫长的, 可能会存在周期模式, 因此石窟寺岩体裂隙发育长期预测也是下一步研究方向。
参考文献:
[1]王茜. 石窟寺窟体破坏机理及稳定性分析 [D]. 西安: 西安建筑科技大学理学院, 2020.
WANG Qian. Damage Mechanism and Stability Analysis of Grottoes [D]. Xi’an: College of Science, Xi’an University of Architecture and Technology, 2020.
[2]王逢睿, 肖碧. 甘肃北石窟寺第165窟岩体稳定性分析研究 [J]. 敦煌研究, 2011(6): 65-69,127.
WANG Fengrui, XIAO Bi. Stability Study of the Rock from Cave 165 in the Beishiku Cave Temple [J]. Dunhuang Research, 2011(6): 65-69,127.
[3]宋文玉. 甘肃庆阳北石窟寺病害分析及防治对策 [C]∥2005年云冈国际学术研讨会论文集(保护卷). 北京: 云冈石窟研究院, 2005: 123-128.
SONG Wenyu. Disease Analysis and Control Countermeasures of North Grotto Temple in Qingyang, Gansu [C]∥2005 Yungang International Symposium Proceedings (Protection Volume). Beijing: Yungang Grottoes Research Institute, 2005: 123-128.
[4]YOUNG P, SHELLSWELL S.Time Series Analysis, Forecasting and Control [J].IEEE Transactions on Automatic Control, 1972, 17(2): 281-283.
[5]LÜKEPOHL H. New Introduction to Multiple Time Series Analysis [M]. [S.l.]: Springer Science & Business Media, 2005.
[6]HOERL A E, KENNARD R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems [J]. Technometrics, 1970, 12(1): 55-67.
[7]CAO L J, TAY F E H. Support Vector Machine with Adaptive Parameters in Financial Time Series Forecasting [J]. IEEE Transactions on Neural Networks, 2003, 14(6): 15061518.
[8]ROBERTS S, OSBORNE M, EBDEN M, et al. Gaussian Processes for Time-Series Modelling [J]. Philosophical Transactions, 2012, 371(1984): 20110550.
[9]HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory [J]. Neural Computation, 1997, 9(8): 1735-1780.
[10]CHUNG J, GULCEHRE C, CHO K. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling [J/OL]. [2022-01-25]. https:∥doi.org/10.48550/arXiv.1412.3555.
[11]于志刚, 张德政, 宋文江, 等. 基于长短期记忆神经网络的油田注水预测 [J]. 吉林大学学报(信息科学版), 2022, 40(1): 77-81.
YU Zhigang, ZHANG Dezheng, SONG Wenjiang, et al. Oil Field Water Injection Prediction Based on LSTM Neural Networks [J]. Journal of Jilin University (Information Science Edition), 2022, 40(1): 77-81.
[12]高金兰, 李豪, 邓蒙. 基于GAVMD-SGRU模型的风电场短期功率预测 [J]. 吉林大学学报(信息科学版), 2021, 39(6): 647-655.
GAO Jinlan, LI Hao, DENG Meng . Short Term Power Prediction of Wind Farm Based on GAVMD-SGRU Model [J]. Journal of Jilin University (Information Science Edition), 2021, 39(6): 647-655.
[13]HUANG S, WANG D, WU X, et al. DSANet: Dual Self-Attention Network for Multivariate Time Series Forecasting [C]∥Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing, China: Association for Computing Machinery. New York, USA: ACM, 2019: 2129-2132.
[14]VASWANI A, SHAZEER N, PARMAR N, et al. Attention is All You Need [J]. Advances in Neural Information Processing Systems, 2017, 30: 5999-6009.
[15]ZHU C, PING W, XIAO C, et al. Long-Short Transformer: Efficient Transformers for Language and Vision [J]. Advances in Neural Information Processing Systems, 2021, 34: 17723-17736.
[16]ZHOU H, ZHANG S, PENG J, et al. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting [J/OL]. [2022-01-05]. http:∥doc88.com/P-28939694659635.html.
[17]VAPNIK V, GOLOWICH S E, SMOLA A. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing [J]. Advances in Neural Information Processing Systems, 2008(9): 281-287.
[18]LECUN Y, BENGIO Y. Convolutional Networks for Images, Speech, and Time Series [J]. The Handbook of Brain Theory and Neural Networks, 1995, 3361(10): 1995.
