隧道侧壁效应下的交通流粘滞特性建模

李振江, 万 利, 吴 涛, 陶楚青

(山东省交通规划设计院集团有限公司 隧道与地下工程设计分院, 济南 250000)

0 引 言

由于交通流之间相互干扰, 如交通流内部交通个体之间、 各交通流之间以及道路边缘固体设施对交通流的干扰, 会使交通流产生粘滞效果, 主要表现为同一交通流的通行速度降低或相邻交通流的通行速度分布不均。因为交通流的粘滞特性对交通状态有很大影响, 所以人们在研究宏观交通流模型时往往引入交通流粘滞力, 以增强模型的可信度。但目前人们对交通流粘滞特性的研究报道较少, 仅有部分学者建立了相应的粘滞力模型。如以自由流速度和换道车辆数为参数, Ke等[1]建立了车辆换道行为下的交通流内部车辆间的粘滞力模型； 以车流密度、 车辆速度、 制动距离和视距为参数, 马健等[2]研究了交通流内部车辆间的粘滞力模型； 以流体力学和牛顿内摩擦力为基础, 龙小强等[3]研究了非机动车道影响下机动车道的粘滞力模型, 程瑶[4]研究了机动车流影响下自行车流的粘滞力模型以及机动车流内部车辆间的粘滞力模型。

特殊路段隧道具有相对封闭、 光线不良且空间有限的特点[5-6]。因此行车过程中驾驶人总会受到隧道侧方墙壁的压迫, 导致驾驶人倾向于降低车速并靠向路中行驶, 常出现占用同向车道线甚至侵占车道中心线的情况, 并在一定程度上造成交通拥堵或事故[7-8]。为减少侧壁效应造成的影响, 吴琼等[9]基于侧壁效应为隧道设计了合理的隧道侧墙图案, 改善了隧道内的视觉环境, 提高了行车安全性。宋子璇等[10]研究并分析了隧道侧壁的图案颜色、 图形和间距问题, 并给出了合适的侧壁设计方案, 增强了驾驶员的速度感和安全感。顾洪源[11]通过数值模拟和理论分析对大断面隧道断面优化及其设计参数进行了较深入的研究, 并对隧道高宽比进行了灵敏度分析。冯强等[12]利用断面仪扫描获得了隧道轴线偏位、 净宽及拱顶与拱腰高度的计算式, 给出了隧道断面轮廓尺寸的量测计算结果。

目前, 对交通流粘滞特性的研究主要立足于常规道路交通流, 而对隧道场景涉猎不足。虽然隧道侧壁对交通流的压迫效应是造成交通事故的重要因素, 但在对隧道安全防护中很少有对隧道侧壁对交通流的粘滞影响研究, 多数是研究隧道侧壁的外观设计或隧道的断面设计。若能建立隧道侧壁间距与隧道交通流粘滞特性的相互关系, 将在提高隧道最外侧车道利用率和隧道运行速度上发挥巨大作用, 并且能在隧道断面优化方面奠定良好基础。基于上述分析, 研究隧道的交通流特性尤其不能忽视隧道侧壁对交通流的干扰。因此, 笔者分析隧道侧壁效应下的交通流粘滞特性, 并对其进行理论建模, 以实现对隧道交通流粘滞特性的定量分析。

1 隧道侧壁效应下交通流粘滞特性分析

在隧道这种特殊路段, 侧壁效应使隧道交通流的粘滞特性更加明显。隧道的侧壁效应是驾驶员感受到隧道侧壁的压迫而引发的一系列驾驶行为改变现象。在侧壁效应作用下, 驾驶员越靠近侧壁感受到的压迫越大, 越倾向于低速行驶, 越远离侧壁感受到的压迫越小, 越倾向于快速行驶。而靠近侧壁的驾驶员为减轻强大的压迫感, 会选择逐渐远离侧壁, 并提高车速。这就是隧道侧壁效应下的交通流粘滞特性(见图1)。

图1 隧道侧壁效应下的车辆运动特性Fig.1 Vehicle motion characteristics under tunnel sidewall effect

在流体力学上, 流体为抵抗流体层之间的相对运动产生了粘滞力, 使流体具有粘滞特性。而隧道侧壁效应下的交通流粘滞特性与流体的粘滞特性相似。因此如果将交通流类比于流体, 可将流体力学中研究流体粘滞特性的理论应用到交通流中。

2 流体粘滞特性模型

2.1 流体粘滞系数模型

雷诺数是粘性流体运动中最重要的物理量, 可得到流体的粘滞系数, 从而表征流体的粘滞特性[13]。因此笔者借鉴流体雷诺数公式推导交通流雷诺数模型, 在此基础上推导交通流粘滞系数。

1883年雷诺发现流体有层流和紊流两种不同的流动状态。当流体速度较小时, 各层流体分层运动, 互不干扰； 当流体速度增大时, 各层流体逐渐发生横向运动, 产生紊流状态。而流体呈何种运动状态, 不仅与流体的速度v有关, 还与流体的密度ρ、 流体圆管直径d和动力学粘滞系数μ等因素有关。考虑这些因素可得到一个无量纲雷诺数

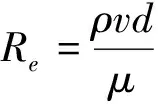
(1)

根据分子运动论, 动力学粘滞系数μ与ρcλ成正比, 其中c为分子运动的平均速度,λ为分子的平均自由程。因此, 经变换, 雷诺数近似于

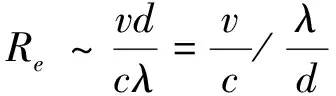
(2)

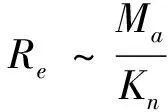
(3)

从而得到流体的粘滞系数为

(4)

2.2 流体粘滞力模型

1687年, 牛顿做了层状流体的粘性实验[13], 在两块相距为d的平行平板之间充满粘性流体, 让下板A静止不动, 让上板B在切向力F的作用下以速度V做匀速直线运动, 实验装置如图2所示。

图2 牛顿流体粘性实验图Fig.2 Experimental diagram of Newtonian fluid viscosity

(5)

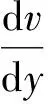
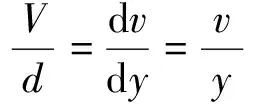
(6)

由于两板间各流体层的速度不同, 因此各层之间会产生切向力τ, 这和两个相对运动的固体之间产生的摩擦力十分相似, 该力也称为粘滞力。由于作用在上板的切应力与板的运动速度成正比, 与两板间距d成反比, 即

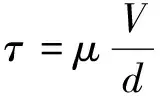
(7)

其中μ为动力学粘滞系数, 表示流体粘度, 是一个物理常量。在此基础上, 各流体层间的切应力为

(8)

由此, 流体力学中流体的粘滞特性, 即粘滞力和粘滞系数具有式(4)所示关系, 粘滞力可由流体的动力学粘滞系数、 速度、 密度和与下板的间距表示。反映到隧道交通流上, 即可认为隧道交通流的粘滞力与交通流的动力学粘滞系数、 速度、 密度以及交通流与隧道侧壁的间距有关。

3 隧道交通流粘滞特性理论建模

3.1 隧道侧壁压迫强度

隧道侧壁效应下交通流的粘滞特性与隧道侧壁给交通流带来的压迫强度有十分密切的关系, 通过上述分析可知, 隧道侧壁给交通流施加的压迫强度与交通流和隧道侧壁之间的距离成反比。因此, 笔者定义一种隧道侧壁压迫场, 将隧道侧壁的压迫强度类比于压迫场场强。根据Li等[14-15]建立的道路边界势场模型, 隧道侧壁产生的压迫场模型E为

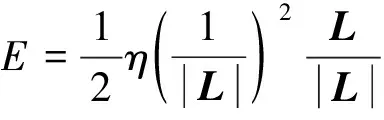
(9)

其中η为场强系数, 取值为3；L为隧道侧壁指向交通流的距离向量。

3.2 交通流粘滞系数模型

除了隧道侧壁的压迫效应对隧道交通流粘滞特性的影响, 交通流本身的粘滞系数也是影响交通流粘滞特性的一个关键因素。笔者将流体雷诺数对应到交通流中, 得到交通流雷诺数ReJ为

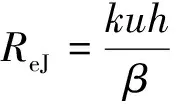
(10)

其中u为交通流速度；h为各交通流占用路段宽度, 近似于车道宽度；β为交通流动力学粘滞系数。对雷诺数的另一种近似表达方式, 在交通流中, 马赫数可用于表示交通流压缩程度的参数, 即交通流压缩系数a表示, 克努生数可用于表示交通流疏密程度的参数, 即交通流密度k表示, 于是交通流雷诺数ReJ还可表示为

(11)

其中交通流压缩系数可根据文献[4], 交通流密度函数表示为

(12)

并且由格林希尔治模型得到

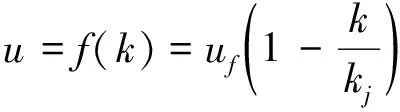
(13)

由此, 隧道交通流动力学粘滞系数求解为

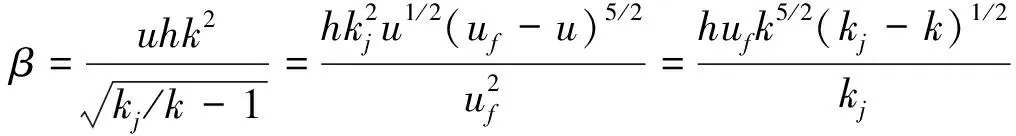
(14)

3.3 交通流粘滞力模型

对流体而言, 切应力与各流体层离下板A的距离呈反比, 即距离越近切应力越大, 距离越远切应力越小。而对隧道交通流而言, 粘滞力与隧道侧壁压迫强度成正比, 即压迫强度越大交通流粘滞力越大, 压迫强度越小交通流粘滞力越小。因此, 受隧道侧壁效应作用的交通流的粘滞力模型ω为

(15)

化简得到

(16)

由于隧道构造形式多样, 有单向和双向以及单车道和多车道之分, 所以以车道为分界线可将隧道中各车道车流分为不同的交通流i。并且由于不同交通流在隧道中的位置不同, 引发其产生粘滞效应的对象也不同。通过对隧道中不同位置交通流粘滞特性的影响因素分析, 最终可将隧道形式分为4种类型。

第1种是单向单车道隧道。在该隧道中, 唯一的交通流受到两侧隧道侧壁的压迫效应。因此该交通流的粘滞力模型为

(17)

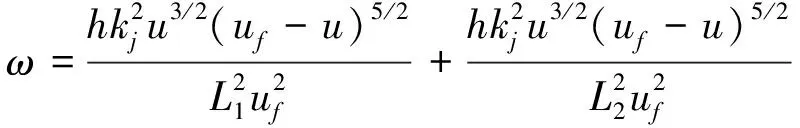
(18)

第2种是单向多车道。在该隧道中, 最左侧和最右侧车道分别受两侧隧道侧壁的影响, 并且由于隧道中有快慢车道的区别, 所以左侧快车道交通流同样会受到右侧慢车道交通流的影响, 此时快速交通流的侧壁为低速交通流。因此假设该隧道交通流从右向左依次标记为交通流1、 交通流2至交通流N, 则各股交通流i的粘滞力模型为

(19)

(20)

第3种是双向两车道。在该隧道中, 双向交通流由于道路中心线的限制几乎不产生粘滞效应, 仅两个单向交通流受到各自方向隧道侧壁的影响。这种情况下, 两个交通流的粘滞力模型相一致, 为

(21)

(22)

第4种是双向多车道。在该隧道中, 两侧最外侧车道同样受到侧方墙壁的压迫效应, 并且由于单向车道数的增多, 导致内侧快车道交通流同样受到旁边慢车道交通流的影响。假设单向交通流从右向左依次标记为交通流1、 交通流2至交通流N, 两侧一致。则该隧道中各车道交通流i的粘滞力模型为

(23)

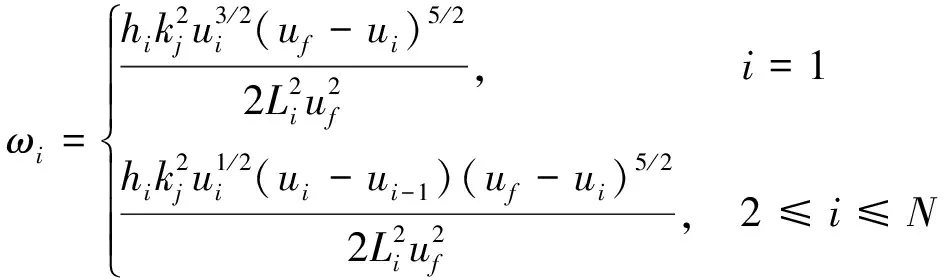
(24)

4 隧道交通流粘滞特性案例分析

4.1 粘滞系数分析

根据笔者的交通流粘滞系数模型, 粘滞系数与交通流的密度或速度以及交通流所在车道宽度有关。根据常规车道宽度信息, 将隧道车道宽度取为3～4 m, 交通流密度取为0～kj,kj=0.075 veh/m, 得到图3所示的车道宽度、 交通流密度和粘滞系数的关系图。并且车道宽度通常取值为3 m、3.25 m、3.5 m和3.75 m, 将这4种情况下粘滞系数与交通流密度的关系曲线绘制在图4中, 以此分析交通流密度对粘滞系数的影响。

图3 车道宽度、 交通流密度与粘滞系数关系 图4 车道宽度固定时交通流密度与粘滞系数曲线Fig.3 Relationship between lane width,traffic flow density and viscosity coefficient Fig.4 Traffic flow density and viscosity coefficient curve when the lane width is fixed

图3和图4表明, 当交通流密度相同时, 随着车道宽度增大, 交通流的粘滞系数成比例增大； 而当车道宽度相同时, 随着交通流密度增大, 交通流粘滞系数呈先增大, 达到最大值, 而后再降低的过程。

4.2 粘滞力分析

根据笔者隧道侧壁效应下的粘滞力模型, 粘滞力与交通流速度、 侧壁压迫强度有关, 其中侧壁压迫强度可通过距离间接反应。将隧道车道宽度取3.75 m, 隧道最外侧交通流1速度取值为0～uf, 设uf=33.3 m/s。并且将隧道侧壁与交通流的间距取为0～1 m。由此得到图5所示的交通流速度、 侧壁间距与粘滞力关系图。并且根据隧道侧壁压迫场模型得到图6所示的侧壁间距和压迫强度曲线图。

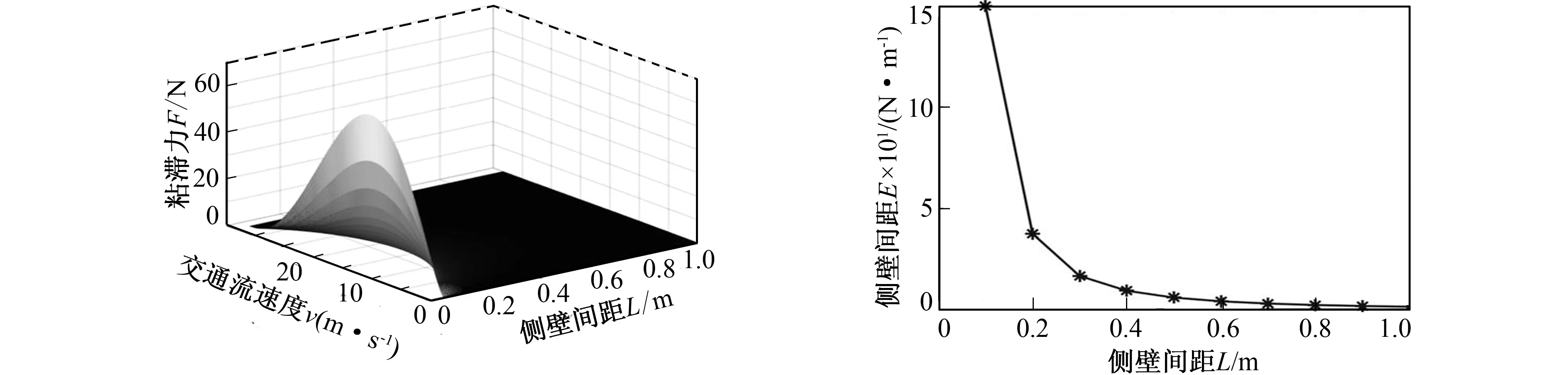
图5 交通流速度、 侧壁间距与粘滞力关系图 图6 侧壁间距和压迫强度曲线图 Fig.5 Relationship between traffic flow velocity,sidewall spacing and viscous force Fig.6 Curve of sidewall spacing and compression strength

图5和图6表明, 当交通流速度相同时, 侧壁间距越小, 受到的压迫强度越大, 粘滞力越大。且压迫强度相同时, 粘滞力随交通流速度增大呈先增大后减小的变化过程。其中粘滞力随速度增加而增加的过程表明, 当交通流密度较大, 造成拥堵时, 粘滞力对速度的影响不明显。这与隧道侧壁效应下的交通流粘滞特性一致。

4.3 粘滞力标定

虽然上述已经分析了交通流粘滞力与隧道侧壁间距和交通流速度的关系, 但由于无法知道隧道中各股交通流的常规粘滞力值, 所以无法为速度已知的隧道设计合理的侧壁间距。如果能标定隧道各股交通流的常规粘滞力, 则根据隧道交通流的设计速度即可求解最佳侧壁间距。由于隧道类型多样, 所以笔者仅选择单向多车道一种类型隧道进行标定。

选取广州广明高速的祈福隧道作为隧道交通流粘滞力标定的原始隧道。该隧道为双洞隧道, 单洞全长1 988 m, 净宽14.5 m, 单向三车道, 车道宽度3.75 m, 设计速度27.8 m/s, 左侧侧壁间距0.5 m, 右侧侧壁间距1.00 m[16]。假设交通流之间的侧壁间距为0.75 m。该隧道设计合理、 常年运行畅通, 可认为在该隧道的结构设计下交通流运行处于平衡状态, 因此由该隧道数据标定的常规粘滞力具有普遍意义, 但也仅限于单向多车道。针对该隧道开发了相应的数字孪生平台, 可采集隧道交通流运行信息, 如图7所示。

图7 广州祈福隧道数字孪生平台Fig.7 Guangzhou Clifford Tunnel digital twin platform

单向三车道被划分为超车道、 快车道和慢车道, 各车道平均速度通过隧道监控平台实时采集, 笔者选取了60 s的监控数据, 采集各车道平均交通流速度, 如表1所示。在此基础上隧道各参数以及常规粘滞力的标定结果如表2所示。

表2标定结果显示, 在单向三车道隧道中, 超车道、 快车道、 慢车道的常规粘滞力大约为0.130 8 N、0.003 2 N和0.094 5 N。基于此, 通过上述粘滞力模型可为其他设计速度已知的单向三车道隧道设计合理的侧壁间距, 也可通过其他运行良好的单向三车道隧道的运行和结构数据反向验证粘滞力的标定结果。但由于数据采集的限制, 这里只根据仅有的隧道数据进行粘滞力标定工作。此方法也适用于其他类型隧道的交通流设计速度和侧壁间距优化工作。

表1 各车道交通流平均速度统计表

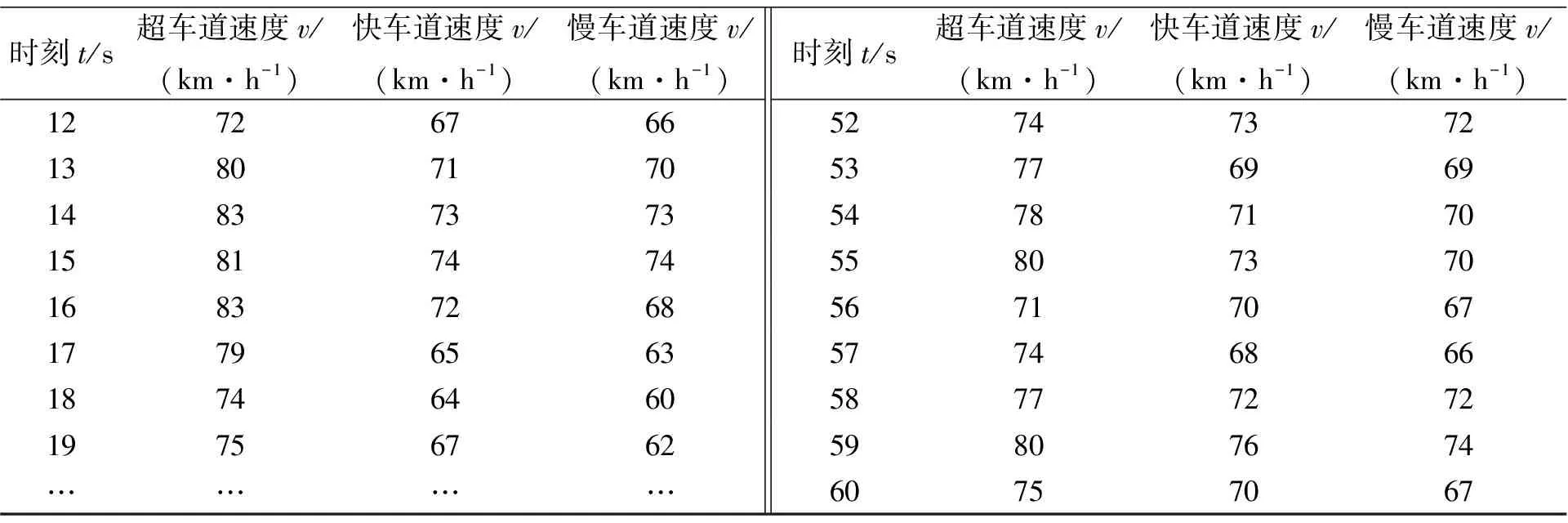
(续表1)

表2 粘滞力标定结果

5 结 语

笔者针对隧道交通流受隧道侧壁压迫从而增大交通流粘滞性的问题, 分析了隧道侧壁效应给隧道交通流运行带来的影响, 并借助流体力学分析流体粘滞特性的相关理论知识, 进行了隧道侧壁效应作用下的交通流粘滞特性理论建模, 构建了隧道侧壁给交通流造成的压迫强度模型, 以及隧道交通流的动力学粘滞系数模型和粘滞力模型。首先进行了隧道交通流粘滞系数和粘滞力的数值实验, 实验结果能直观表达交通流粘滞系数与车道宽度和交通流密度的关系以及交通流粘滞力与侧壁间距和交通流速度的关系； 其次进行了隧道粘滞力标定实验, 实验结果表明单向三车道隧道中三股交通流的常规粘滞力分别为0.130 8 N、0.003 2N和0.094 5 N, 该结论可作为单向三车道隧道断面优化的理论基础。未来研究可采集大量的不同类型隧道的运行和结构数据, 进一步优化并标定其他类型隧道交通流的常规粘滞力。

参考文献：

[1]KE Hongtang, LIU Xiaohe, GUO Mingming, et al. A New Traffic Model with a Lane-Changing Viscosity Term [J]. Chinese Physics B, 2015, 24(9): 592-598.

[2]马健, 张丽岩, 李克平. 考虑粘滞与压缩特性的改进宏观交通流模型研究 [J]. 公路工程, 2015, 40(6): 64-70.

MA Jian, ZHANG Liyan, LI Keping. A Study on Improved Macroscopic Traffic Flow Model Considering Viscosity and Compressive Properties [J]. Highway Engineering, 2015, 40(6): 64-70.

[3]龙小强, 晏启鹏. 非机动车道对机动车道干扰的流体内摩擦模型 [J]. 中国公路学报, 2002(1): 103-105.

LONG Xiaoqiang, YAN Qipeng.Liquid Inner-Friction Model about Non-Maneuverable Lane Interference with Motor Lane [J]. China Journal of Highway and Transport, 2002(1): 103-105.

[4]程瑶. 交通流压缩与粘滞特性研究 [D]. 长春： 吉林大学交通学院, 2007.

CHENG Yao. Study on Compressibility and Viscosity of Traffic Flow [D]. Changchun: College of Transportation, Jilin University, 2007.

[6]XU L, XU X, DING C, et al. Spatial-Temporal Prediction of the Environmental Conditions Inside an Urban Road Tunnel during an Incident Scenario [J]. Building and Environment, 2022, 212: 108808.

[7]陈聪. 基于视觉信息的高速公路隧道行车安全评价指标研究 [D]. 上海： 同济大学交通运输工程学院, 2011.

CHEN Cong. Research on the Evaluation Index of Highway Tunnel Driving Safety Based on Visual Information [D]. Shanghai: College of Transportation Engineering, Tongji University, 2011.

[8]赵飞, 李洋洋, 韩晖. 基于交通事故数据的高速公路隧道路段安全性分析 [J]. 北方交通, 2021(11): 83-86.

ZHAO Fei, LI Yangyang, HAN Hui. Safety Analysis of Expressway Tunnel Section Based on Traffic Accident Data [J]. Northern Communications, 2021(11): 83-86.

[9]吴琼, 潘晓东, 杨辉, 等. 基于侧墙效应的隧道行车安全实验研究 [J]. 公路工程, 2013, 38(5): 99-102,118.

WU Qiong, PAN Xiaodong, YANG Hui, et al. Research on Driving Safety Experiment of Tunnel Based on Sidewall Effect [J]. Highway Engineering, 2013, 38(5): 99-102, 118.

[10]宋子璇, 潘晓东, 李少帅, 等. 基于侧墙效应的隧道行车安全评价基础研究 [J]. 公路工程, 2010, 35(3): 10-13,18.

SONG Zixuan, PAN Xiaodong, LI Shaoshuai, et al. Study on Driving Safety Evaluation Based on Tunnel Sidewall Effect [J]. Highway Engineering, 2010, 35(3): 10-13,18.

[11]顾洪源. 大断面小净距隧道断面优化及其设计参数研究 [J]. 铁道标准设计, 2013(2): 85-89.

GU Hongyuan. Section Optimization and Design Parameters Study on Large-Spanned Small-Spaced Twin-Tube Tunnel [J]. Railway Standard Design, 2013(2): 85-89.

[12]冯强, 吴晓锁. 公路隧道断面轮廓尺寸量测计算 [J]. 公路交通科技(应用技术版), 2011, 7(9): 161-163.

FENG Qiang, WU Xaiosuo. Measurement and Calculation of Profile Dimensions of Highway Tunnels [J]. Journal of Highway and Transportation Research and Development (Application Technology Edition), 2011, 7(9): 161-163.

[13]路峻岭, 顾晨, 秦联华, 等. 关于流体力学黏滞及伯努利方程演示实验 [J]. 物理与工程, 2020, 30(1): 80-86,92.

LU Junling, GU Chen, QIN Lianhua, et al. Demonstration Experiments on Fluid Dynamics Viscosity and Bernoulli Equation [J]. Physics and Engineering, 2020, 30(1): 80-86,92.

[14]LI Linheng, GAN Jing, YI Ziwei, et al. Risk Perception and the Warning Strategy Based on Safety Potential Field Theory [J]. Accident Analysis and Prevention, 2020, 148: 105805.

[15]LI Linheng, GAN Jing, JI Xinkai, et al. Dynamic Driving Risk Potential Field Model under the Connected and Automated Vehicles Environment and Its Application in Car-Following Modeling [J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 23(1): 122-141.

[16]罗立娜. 广明高速公路祈福隧道主体结构工程设计 [J]. 广东公路交通, 2012(1): 31-34.

LUO Lina. Structural Design of Qifu Tunnel of Guangzhou-Gaoming Expressway [J]. Guangdong Highway Communications, 2012(1): 31-34.