2022年新高考卷解三角形试题的多解与拓展*
2023-01-16广东省中山市实验中学528404杨沛娟广东省中山市濠头中学528437
广东省中山市实验中学 (528404) 杨沛娟 广东省中山市濠头中学 (528437) 张 宇
1.试题呈现
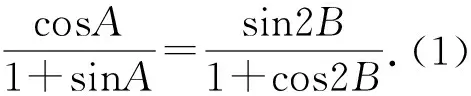
2.解法分析

3.解法探究
3.1 第(1)题解法
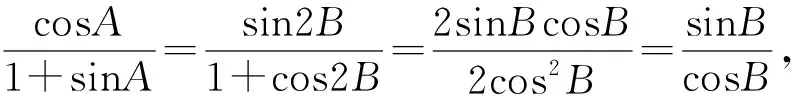
评注:此解法用到了诱导公式及三角形的内角和公式,思路清晰,解法自然.
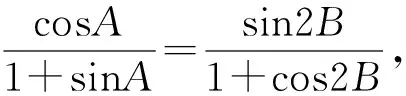


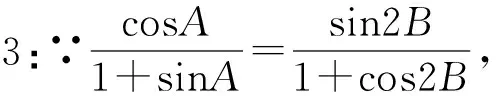

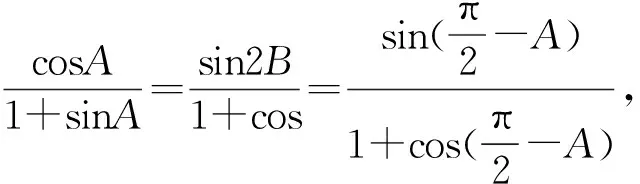
评注:此法将已知条件转化为两条直线的斜率问题,数形结合,体现了数学内部各版块知识的一致性,能较好地考查到学生的数学思维能力.

评注:此法将已知条件转化为两角和与差的正弦及余弦,同时巧妙地对角进行转化,过程简洁,易于理解和掌握.

评注:此法运用同构思想,通过构造函数得到两角的关系,简洁明快.
3.2 第(2)问解法
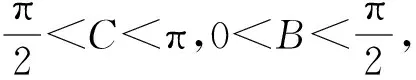
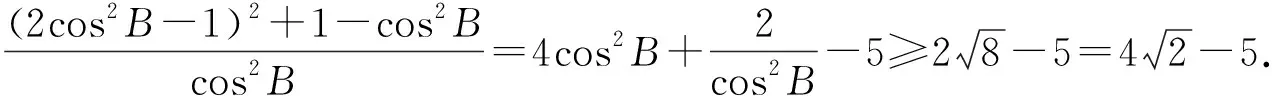
评注:此法由正弦定理化边为角,通过角的换元代换,将三个变元转化成一个变元,然后运用基本不等式得出最值,思路清晰,易于理解,需注意的是取等的条件.
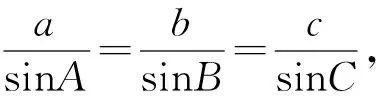

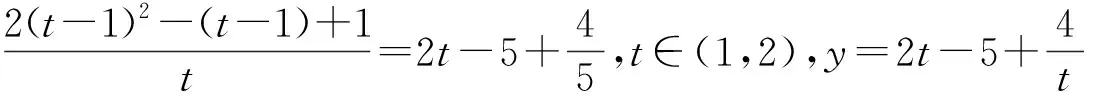
评注:此法运用正弦定理,再运用降幂公式,通过换元将其转化为函数的最值问题,然后用函数的单调性解决问题.



评注:此法将已知条件进行转化,然后化弦为切,运用基本不等式使问题得到解决.

评注:对于含有二次式的分式形式的最值问题,用判别式法是一种比较常见的方法.

评注:此法本质上与解法3是一样的.也可以由判别式法求得最值.
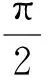
评注:解法6和解法1本质上是一致的,都是通过转化,然后直接用基本不等式求得问题的结论.
4 试题拓展
以上分别列举求解第(1)问和第(2)问的6种常见的方法,由于第(1)小问和第(2)小问相对独立,因此,在理论上完成此题的解法很多.限于篇幅,不再例举,留给读者作为练习.
经过进一步的分析探究可知,此题还可以进行如下的拓展.
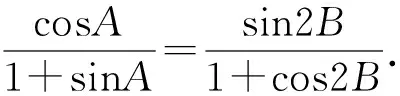
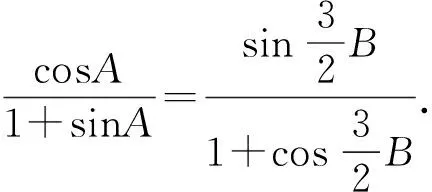
5 教学建议
解三角形是近年高考试题中经常出现的试题,这部分内容主要涉及到正弦定理,余弦定理,面积公式及射影定理等.因此教师在进行这类问题的教学或复习时,要加强基础知识方面的练习,基础知识扎实了,解决此类问题的时候,就能尽可能地避免解题过程中出现多解、错解或漏解的情况.
