赏析同时具有max和min符号的不等式问题*
2023-01-16北京市第一0一中学怀柔分校101407李加军
北京市第一0一中学怀柔分校 (101407) 李加军
在一些数学竞赛的不等式证明中,常常会在条件或结论中同时出现最大值max和最小值min符号,使得学生心理产生畏惧感.下面结合具体实例分析解决这类问题常用的数学方法和策略.
一、构造法
根据所给条件,构造相应的函数,利用函数的性质进行分析,从而得出结论.
例1 (2016美国数学奥林匹克竞赛试题)已知a,b,c∈R+,且max(a,b,c)≤4min(a,b,c),证明或者否定2ab+2bc+2ca≥a2+b2+c2.
解:结论是肯定的.证明如下:不妨设a≥b≥c>0,则c≤b≤a≤4c.令f(a,b,c)=a2+b2+c2-2ab-2bc-2ca,让上式中b,c固定,a变化,视作a的二次函数,记为g(a)=a2-2(b+c)a+b2+c2-2bc,其对称轴为a=b+c,由于a∈[c,4c],所以gmax(a)=max{g(c),g(4c)},又g(c)=c2-2(b+c)c+b2+c2-2bc=b(b-4c)≤0,g(4c)=16c2-6(b+c)c+b2+c2-2bc=(9c-b)(c-b)≤0,所以f(a,b,c)=g(a)≤0,即a2+b2+c2-2ab-2bc-2ca≤0,所以2ab+2bc+2ca≥a2+b2+c2.
例2 (第48届IMO试题)给定实数a1,a2,…,an,对每个i(1≤i≤n),定义:di=max{aj|1≤j≤i}-min{aj|i≤j≤n},并令d=max{di|1≤i≤n}.
(1)证明:对任意实数x1,x2,…,xn,有
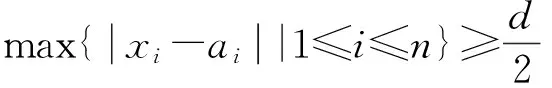
(2)证明:存在实数x1,x2,…,xn,使得式①中的等号成立.
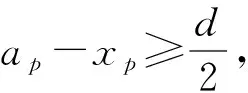

二、反证法
提出与结论相反的假设,利用已知条件与假设进行推理,得出矛盾.
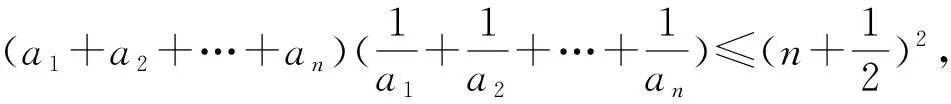
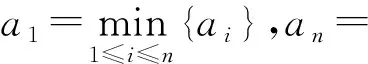
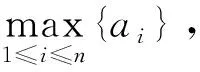

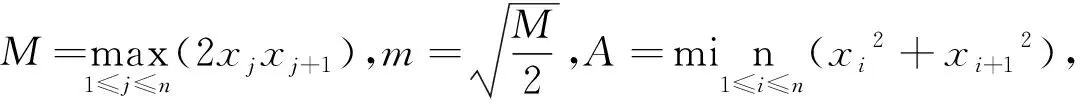

(2)若∃k∈N+,1≤k≤n,使得xk
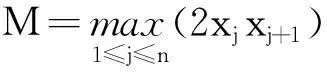
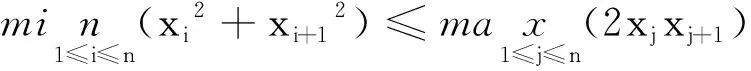
例5 (2008北大自招试题)已知a1+a2+a3=b1+b2+b3,a1a2+a2a3+a3a1=b1b2+b2b3+b3b1,且min(a1,a2,a3)≤min(b1,b2,b3),求证:max(a1,a2,a3)≤max(b1,b2,b3).
证明:不妨设a1≥a2≥a3,b1≥b2≥b3,则a3≤b3,下证:a1≤b1.
用反证法.若a1>b1,则构造两个函数:f(x)=(x-a1)(x-a2)(x-a3),g(x)=(x-b1)(x-b2)(x-b3),由已知条件a1+a2+a3=b1+b2+b3,a1a2+a2a3+a3a1=b1b2+b2b3+b3b1,得f(x)=g(x)+b1b2b3-a1a2a3.
一方面,f(a1)=g(a1)+b1b2b3-a1a2a3=0,f(a3)=g(a3)+b1b2b3-a1a2a3=0,故g(a1)=g(a3),另一方面,g(a3)=(a3-b1)(a3-b2)(a3-b3),a3-b3≤0,a3-b2≤0,a3-b1≤0,故g(a3)≤0,g(a1)=(a1-b1)(a1-b2)(a1-b3),a1-b1>0,a1-b2>0,a1-b3>0,故g(a1)>0,这与g(a1)=g(a3)矛盾.因此a1≤b1,即max(a1,a2,a3)≤max(b1,b2,b3).
三、分析法
从所证明的结论出发,步步寻求题目结论成立需要的充分条件,直至最后得到一个既定的事实.

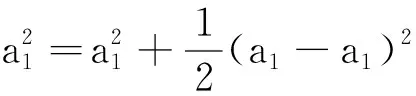
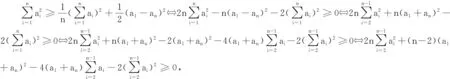
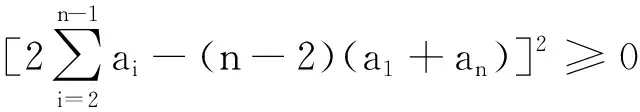
四、放缩法
利用最大值和最小值对一般值进行替换放缩,结合已知条件得到需要证明的结论.

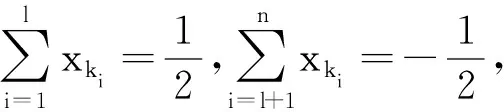
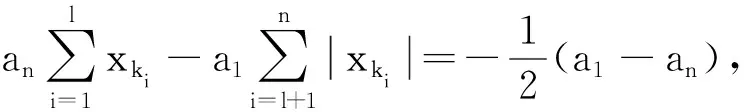

在平常学习中,我们要牢牢掌握数学基本思想、基本方法和基本策略,加强深度学习和深度思考,不断提升个人分析问题、解决问题的能力,发展数学思维,培养数学核心素养.
