对一道经典试题的再研究
2023-01-16江苏省连云港市外国语学校222003
江苏省连云港市外国语学校 (222003) 陈 洋
《普通高中数学课程标准(2017年版)》要求“提升学生的数学素养,引导学生会用数学的眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.”“高中数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新意识,提升数学学科素养.”而解题教学又是提升数学学科素养的载体,因此,在平常的教学中,我们要善于发现有价值的数学问题,通过有效的教学手段,让深度学习发生,进而发展学生的核心素养.
1 习题呈现
题目过点P(2,1)的直线l交x轴,y轴的正半轴于A,B两点,O为坐标原点.求△AOB面积S取最小值时直线l的方程.
这是笔者在开学初新授苏教版《选择性必修一》(2019)直线方程章节时选的一道经典题目,这道题题干简洁、内涵丰富,解法颇多,直线搭台,不等式唱戏,是难得一道培养学生思维品质的好题.
2 解法探究
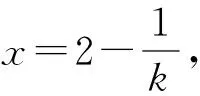

点评:从直线方程的点斜式入手,求出与x轴,y轴交点,代入面积公式,再利用基本不等式,这里要注意“一正,二定,三相等”的条件.

点评:直接从截距入手,利用基本不等式求解,运用基本不等式时,一定要注意成立条件.

点评:将其中一个变量用另一个变量表示,即消元,它是处理二元变量问题的基本方法,再通过添项,拆项构造基本不等式进行求解.

点评:用函数方程思想,转化成一元二次方程,利用根的判别式求解,注意△≥0只是保证方程有大于2的根的必要条件,要对S=4时,实数a是否大于2进行检验.

点评:由“1”想到三角代换,注意对参变量角θ的范围限制,再利用基本不等式求解.

点评:巧妙地构造定比,利用定比分点坐标公式,结合基本不等式求解.




图1
点评:引入“角参数”,利用解三角形知识,构造基本不等式求解.

点评:将其中一个变量用另一个变量表示,即消元,它是处理二元变量问题的基本方法,再利用导数求最值.
3 变式探究
变式(1)求过点P(2,1)且在两正半轴上的截距之和最小的直线方程;
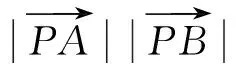
(3)求过点P(2,1)且与两坐标轴围成一等腰直角三角形的直线l方程;
(5)过点P(6,4)作直线l交直线y=2x于第一象限内的点A,交x轴正项于点B,求△AOB面积最小值时l的方程;
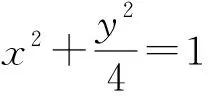
4 结语
在上述解题中,不同层次的学生都能获得不同程度的知识构建机会,让他们感受到数学活动的快
乐和对数学学习的兴趣,激发了对数学探究活动的欲望.纵观上述解法,有必要对其进行比较、评价、筛选,甄别出最优的解法,或提出这些解法中易错点、注意点,或提炼出问题探索中发现的有价值的数学思想方法,培育学生的数学学科素养.课堂上数学题并不在于多,而在于充分挖掘每一道题的内涵与外延,使每一道题的功能达到最大化,对在课堂中的数学问题,不是简单地给学生讲懂,而要讲变化(式)、讲拓展、讲思辨(方法),使学生以不变应万变,只有这样,才达到“授之以渔”的目的.
