基于函数思想的一道数列检测试题的求解
2023-01-16福建省福清第三中学350315何文昌
中学数学研究(江西) 2023年2期
福建省福清第三中学 (350315) 何 灯 何文昌
数列是一种特殊的函数,在解决数列问题时,要善于利用函数的知识,函数的观点,函数的思想,以它的概念、图象、性质为纽带,架起函数与数列的桥梁,揭示它们的内在联系,从而为解答数列问题提供新的途径.
基于函数思想的引领,本文给出福建省部分地市2022届高三毕业班诊断性联考(福建省省检)第12题一个直观的求解,展示了数学思想在问题求解中的强大作用,揭示了此类问题的本质.

A.{S2n}是递增数列 B.{S2n-1}是递减数列
C.{bn-cn}存在最大项 D.{bn-cn}存在最小项

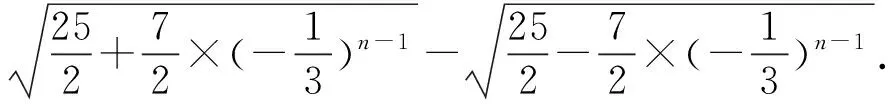
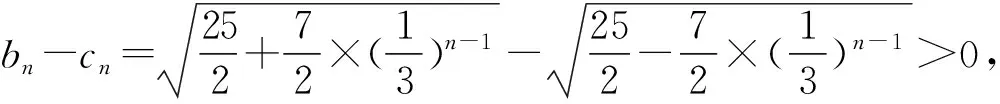
求解本题有两个难点,其一:数列{bn}及{cn}通项公式的推导,需要将题设条件进行合理的简化、合并;其二:将Sn与bn-cn表示出来,并判断其单调性.对于大部分同学而言,要突破上述两个难点并非易事.
下面我们尝试从函数思想入手,借助函数图象的直观特点,对问题进行剖析.

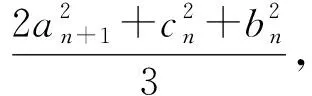
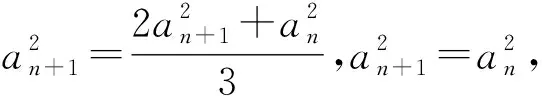

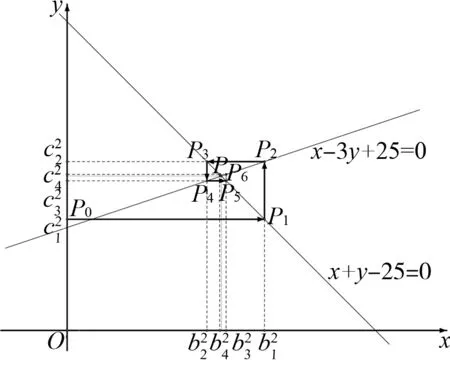
图1


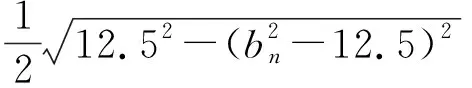
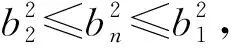
基于函数思想,借助于函数的图象、性质,我们实现了篇首问题的直观求解.在数列问题的求解中,我们可以尝试用函数的观点来看待,用研究函数的方法来研究,这样能够让我们站在更高的位置总览问题全局,为探索解决问题指明方向.
