从“题目解决”到“问题本质”的探究
——对2022广东省一模导数题的背景思考
2023-01-16广东省东莞实验中学523120蔡瑞卿
广东省东莞实验中学 (523120) 蔡瑞卿
一 原题呈现
题目已知f(x)=lnx+ax+1,f′(x)为f(x)的导函数.
(1)若对任意x>0都有f(x)≤0,求a的取值范围;
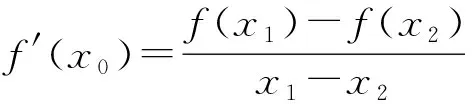
本题是2022年广东一模第21题,考察学生运用导数工具探索函数性质的能力,解题过程涉及零点存在定理,导数运算及其几何意义,运用导数研究函数的单调性等知识.设问中涉及x1,x2,a,x0四个变量,结构新颖,解题思路开放,解题过程蕴含了数形结合,分类讨论,转化与化归,函数与方程等丰富的数学思想.第(1)问常规设问答题起点较低,考查学生对基础知识,基本方法和基本技能的掌握,无论是通过分类讨论,还是分离变量法,学生基本上能够理清思路快速解决问题.第(2)问变量较多,解决问题的突破口难以寻找,思路的方向不易寻找,需要学生在把握基本思路的基础上,通过运算找到解决问题的契机,考查到学生分析问题和解决问题的能力,以及逻辑推理,数学抽象,数学运算等核心素养.
解:(1)易得a≤-1(过程略).
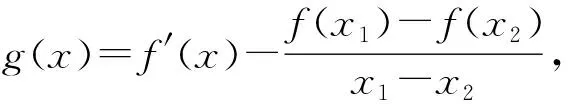

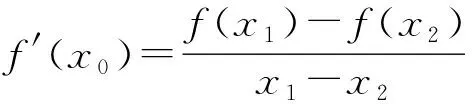
二 背景分析
该题第(2)问证明的结论实际是大学《数学分析》课程中的拉格朗日中值定理,该定理是高考函数与导数压轴题中的高频选题背景,在近些年全国卷中屡有出现,《普通高中数学课程标准(2017年版)》对高中数学课程的结构进行变革,也在选修课程A类“导数与微分”一章中引入拉格朗日中值定理,指导学生运用拉格朗日中值定理证明不等式,为学生将来步入大学学习高等数学打下坚实基础.这样的调整是对拉格朗日中值定理重要性的有力证明,一线教师应当能够理解运用该定理并将其作为教学教研的有力工具.
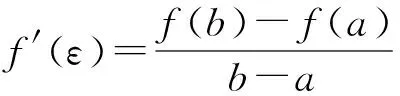
三 真题举例
近些年以拉格朗日中值定理为背景的高考题频繁出现,例如:
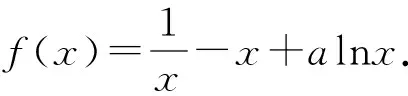
(1)讨论f(x)的单调性;

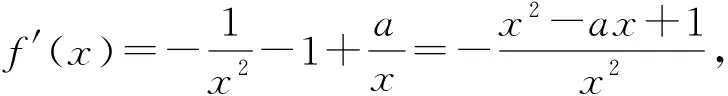
例2 (2017年新课标全国Ⅱ卷文)设函数f(x)=(1-x2)ex.
(1)讨论f(x)的单调性;
(2)当x≥0时,f(x)≤ax+1,求a的取值范围.

例3 (2016全国新课标Ⅱ卷文科21题)已知函数f(x)=(x+1)lnx-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若x∈(1,+∞),f(x)>0,求a的取值范围.
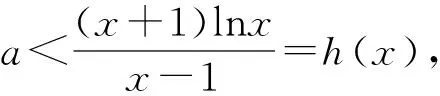
四 变式研发
对2022广东一模导数题的背景发掘,一方面可以开阔学生解决问题的思路,提高学生对高观点知识的兴趣,加强学生进一步学习数学的信心;另一方面借助拉格朗日中值定理,可以更方便地对题目进行变式教学,为一线教师对高考题的教学研究提供一般路径和方法.例如通过观察用拉格朗日中值定理解决16-18年全国卷导数压轴题的步骤发现,只要对解题过程中的g(x)进行不同类型的函数变换,就可以生成不同拉格朗日中值定理背景的恒成立问题,形成丰富的高观点变式训练题目.
变式1 已知函数f(x)=xlnx-a(x-1),若x∈(1,+∞),f(x)>0,求a的取值范围.(取g(x)=xlnx,答案:a≤1)

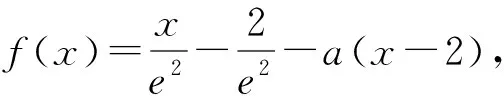
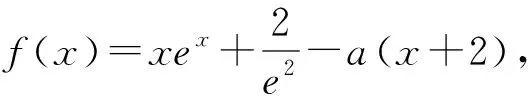
综上可见,“把握数学本质,启发思考,改进教学”是新课标的重要理念,高观点背景的发掘和方法的探究,有助于帮助学生揭示问题的数学本质,启发学生找到解决问题的正确方向和先进方法,更加深刻地理解问题,提升学生学习数学的兴趣,具备更广阔的数学视野.为此,一线教师应当把握合适的契机,为学生探究和掌握高观点知识做好铺垫,找准初等数学与高等数学的结合点,为学生学习更丰富的数学知识搭建好的平台.同时,教师只有具备了更多高观点的数学知识,对问题的理解才能更接近本质,进而提升自身专业能力和教学水平.
