巧用“两招”突破解三角形的解题障碍点
2023-01-16福建省永春第一中学362600张隆亿
福建省永春第一中学 (362600) 张隆亿
解三角形问题,能有效考査学生对正弦定理、余弦定理和三角恒等变换等基础知识,常出现在选择题、填空题与解答题之中,备受命题者的青睐.本文结合解三角形试题特点,梳理破解解三角形问题障碍点的两招.
第一招:利用方程思想突破解三角形的解题障碍点
涉及多个三角形的解三角形试题,往往是通过解条件充分的三角形进而求出其他的边角,抓住条件较丰富的两个三角形以及它们公共的边角.常见的解法是运用方程思想设元并根据题中的等量关系(等角、角互补、作平行线、作高、向量关系、面积关系、建立平面直角坐标系等)列方程(组)求解问题.因此,抓住方程思想的本质,提高思想认识,强化方程思维意识是解决这类问题的关键.
例1 (2022·泉州质检二)在ΔABC中,角A,B,C所对的边分别为a,b,c,且2acosB=2c-b,△ABC内一点P满足:PB⊥PC,∠APC=120°,且AC=3AB=3,求tan∠ACP.
分析:如图1,涉及∠ACP的三角形ΔAPC中,已知的条件只有AC=3,∠APC=120°,显然条件不够,但与△APC有公共边,与△ABP也有两个条件AB=1,∠APB=150°.因此,应该抓住△APC、△APC这两个三角形找出等量关系,列方程,进行求解.结合正弦定理及三角恒等变换,三角恒等变换即可求A=60°.

图1

例2 (2021·高考卷Ⅰ改编)记△ABC的内角A,B,C所对的边分别为a,b,c.已知点D在边AC上,b2=ac,AD=2DC,BD=b,求cos∠ABC.
分析:如图2,涉及∠ABC的三角形只有△ABC,但其条件不够.而三角形△ABD、△BCD涉及主要条件AD=2DC,BD=b,所以以退为进,通过△ABD、△BCD、∠ABC三个三角形中的两个三角形,找出a,b,c之间的联系.该题属于爪型三角形模型,常见有以下解法.

图2

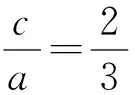


图3
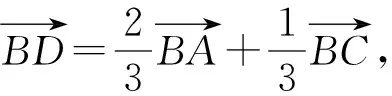
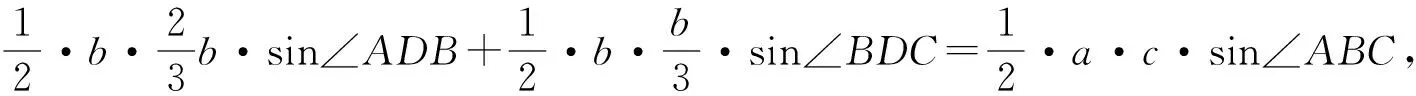
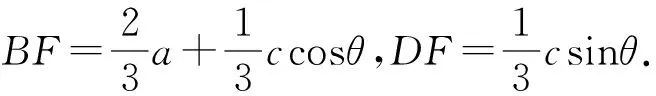

图4
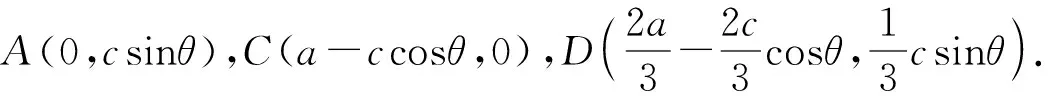
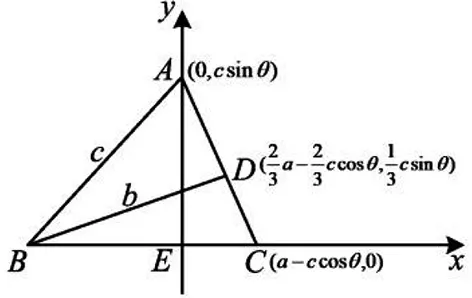
图5
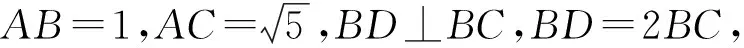

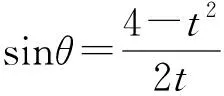
图6
例4 (2015·新课标Ⅰ)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是.
分析:如图7,平面四边形ABCD四个角及边BC确定,AD在△BCE内平行滑动,涉及AB的有△ABD,△ABC,但条件仍然不够,且较难整合所有条件,而△ADE却可以.因此抓住△ADE,△BCE这两个三角形找出等量关系,列方程,进行求解.
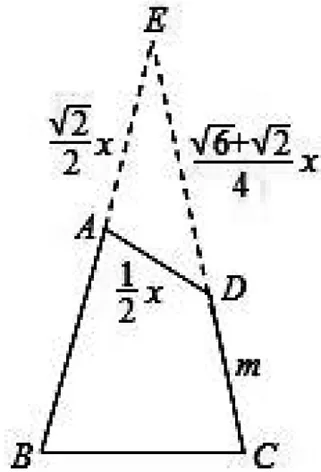
图7

第二招:利用动态三角形背景突破解三角形的解题障碍点
涉及动态三角形问题直接求解往往比较困难,一般运用化归与转化的数学思想,将动态三角形转化为定的轨迹或位置.常见动态三角形背景如下:
(1)圆:动态三角形中只知道一边及其对角;动态三角形中一边确定另外两边互相垂直;动态三角形所在的四边形对角互补;动态三角形中一边确定另外不等两边满足倍数关系(阿氏圆);推广的托勒密定理(四边形ABCD中,AC·BD≤AB·CD+AD·BC,当且仅当四边形ABCD为圆内接四边形,等号成立);题设条件等.


图8
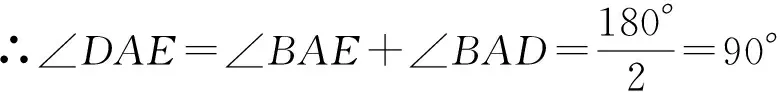
(2)椭圆:动态三角形中一边固定,另外两边和为常数;动态三角形中某两个角的正切之积为(0,1)常数(椭圆第三定义)等.

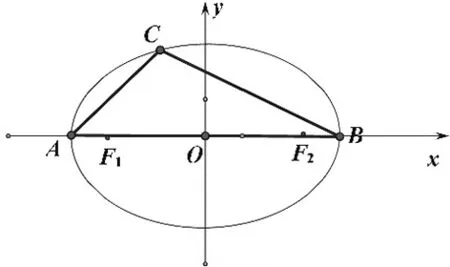
图9

(4)三角形:动态三角形所在的四边形延长某两边交于一点,所得的三角形不变.

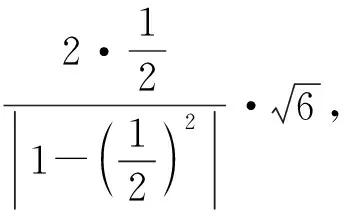
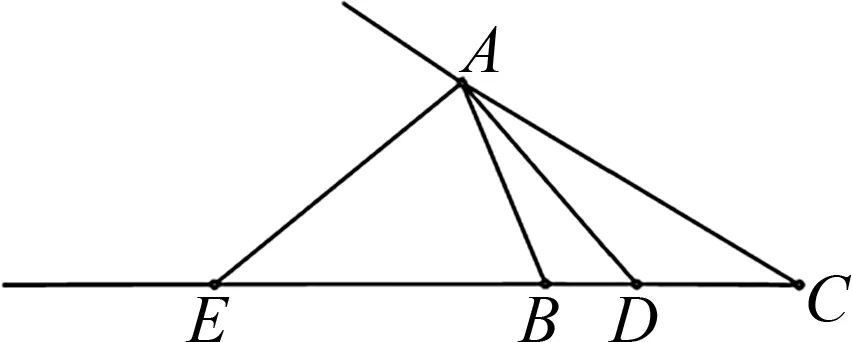
图10
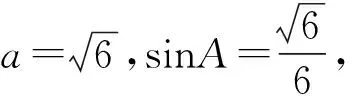
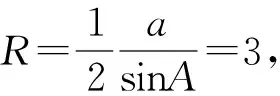

图11

例4另解:如图12,抓住动态四边形ABCD始终在确定的三角形△BCE内平行滑动,运用极限思想可便捷得出答案.

图12

例5 (2022·蚌埠校级模拟)在△ABC中,a,b,c分别为内角A,B,C的对边,若a+c=4,2sinB=sinA+sinC,则△ABC的面积的最大值为.
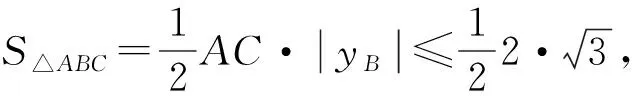
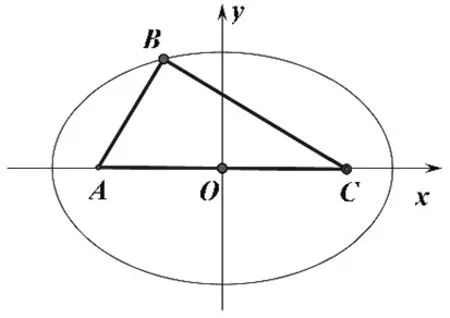
图13
变式在△ABC中,a,b,c分别为内角A,B,C的对边,若a-c=2,b=4,O为AC,则OB的取值范围为.
析解:由BA-BC=2 简而言之,涉及多个三角形的解三角形问题,正常思路受阻时,可以抓住条件充分的两个或以上三角形,运用函数方程思想突破解题障碍;涉及动态三角形的解三角形问题的解题关键是抓住动点的轨迹,运用轨迹思想、极限思想等方向思考解决问题的方法,化繁为简、化难为易,从而突破解题障碍.
