基于APOS理论的零点存在性定理教学要点
2023-01-16江西师范大学数学与统计学院330022魏素云易桂生
江西师范大学数学与统计学院 (330022) 魏素云 易桂生
一、APOS理论要义
APOS理论是由美国的杜宾斯基等人在数学教育与研究实践中发展形成的.该理论依据学生学习的心理建构过程,提倡教师在教学中,应以学生为主体,让学生主动探究、理解和掌握知识.其教学流程如图所示:
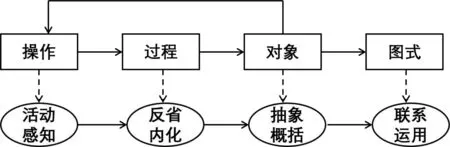
“操作”阶段(Action),学生需要通过操作来感知事物,理解所学内容的意义.通过操作,学生对何为函数零点和零点存在的条件会有一定的感性认识,同时,教师应向学生提供符合函数零点存在性定理学习的材料或者情景动画,并相应地设计出适合学生探究的学习活动,由此为归纳概括所学概念提供建构的固着点.
“过程”阶段(Process),强调学习者应把“操作”阶段中的感受进行反省内化.老师教学中,可以用问题串的形式,帮助学生从操作对象中跳出来,引发学生的思维逐步深入.
“对象”阶段(Object),学生通过对数学活动的思考、分析、比较及抽象之后得到函数零点的概念和零点存在性定理的条件,并在教师的引导下能用较严谨的数学语言准确地表述出其定义及存在性定理.
“图式”阶段(Scheme),学习者头脑中函数零点相关内容将以一种综合的图式呈现,并在其知识体系中占据独特的位置.这一阶段,学生对函数零点的概念有较为完整的认知结构或认知框架,教师在教学中相应地应可通过练习让学生达到对函数零点存在性定理的理解,由此帮助学生形成零点概念的整体图式.
二、教学目标及重、难点
1.教学目标
(1)能在结合具体的实例中,掌握函数零点的定义.
(2)能借助操作活动,归纳总结出“函数零点存在性定理”,并能理解该定理的条件.
(3)在辨析和操作的过程中感悟其数学思想方法,并养成严谨性的学习习惯、提高数学抽象和直观想象素养.
2.重点:函数零点存在性定理.
3.难点:函数零点存在条件的探究.
三、定理的教学过程
1.新课引入
问题1 2x-y-6=0表示什么?x=3表示什么?
预设:2x-y-6=0表面上看是方程.同时x=3也是二元一次函数与x轴交点的横坐标.
问题2 方程2x+2x-6=0是否有实根?
预设:部分学生会把该方程转化为两个函数y=2x与y=-2x+6,再数形结合判定出方程根所在的区间范围,也有学生想通过作出y=2x+2x-6的图像,但发现很困难.
设计意图:问题1主要是为函数零点概念做铺垫,更重要的是引导学生认识到方程与函数之间的特殊关系.问题2则是引发学生的认知冲突.
2.感知定理
方程和函数可以互相转化,求方程的根就是求函数与x轴的交点的横坐标.
让我们在直角坐标系中画一画,以线条来代替函数曲线,怎样画曲线才能与x轴有交点?
预设:师生根据图像,选择有交点的情况,并引导学生进行分类讨论.
问题3 什么条件下与x轴一定有交点呢?
预设:端点一上一下的时候.
问题4 在直角坐标系中怎样判断端点是在x轴一侧呢?
预设:根据函数值的符号来判断.
问题5 我们如何用一个统一的式子来表达A、B两点函数值是异号呢?
问题6 具备上述特征的函数y=f(x)的图像与x轴在区间(a,b)上一定有交点吗?
设计意图:将函数零点存在性定理作为解决课堂探究问题的过程性知识,让学生在动态操作中观察,探索和发现函数端点处的函数值,函数连续性对定理的影响.
3.定理形成
总结:对于函数y=f(x),把使f(x)=0的实数x叫做函数的零点.若函数y=f(x)在闭区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则f(x)在区间(a,b)内至少有一个零点.
设计意图:关注学生判定定理的形成过程,通过问题串,引导学生的思维逐渐深入,经历从具体到抽象并归纳总结出零点的判定定理.
4.定理辨析
结合函数图象,判断以下命题的正误性,若不正确,请通过函数图像举出反例.
(1)若函数y=f(x) 在[a,b]上满足f(a)·f(b)<0,则它在区间(a,b)内一定有零点.
(2)若函数y=f(x)在[a,b]上的图象连续,且它在区间(a,b)内有零点,则f(a)·f(b)<0.
(3)若函数y=f(x)在[a,b]上的图象连续,且f(a)·f(b)<0,函数y=f(x)在区间(a,b)内存在唯一零点.
设计意图:通过以上判断既是对学习活动情况的总结,又是对函数零点存在性定理作进一步的认识,(1)函数图象连续;(2)结论不可逆;(3)零点个数不确定.由此让学生的学习能达到概念的精致化目的.
5.定理运用
例1 若a A.(a,b)和(b,c)内 B.(-∞,a)和(a,b)内 C.(b,c)和(c,∞)内 D.(-∞,a)和(c,∞)内 解:由a 图1 设计意图:上述例题及变式是利用零点存在性定理判断零点是否落在某个区间,并能通过存在零点的区间求函数解析式中变量的取值范围,由此不仅可以通过零点存在性定理来判断,也可以采用数形结合的方法,通过图像的平移得出结论. A.0个 B.1个 C.2个 D.3个 变式讨论方程2x+2x-6=0解的个数与分布情况. 解:一方面,考察函数f(x)=2x+2x-6,其零点就是方程2x+2x-6=0的解.计算得f(1)=-2<0,f(2)=2>0.可见该函数在(1,2)内有零点.另一方面,由于2x单调递增而2x-6也单调递增,因此f(x)=2x+2x-6单调递增,所以该函数在(1,2)内恰有一个零点. 预设:本变式可通过学生练习并板书讲解完成. 设计意图:本例题及变式目的是强化通过两个函数图象的交点问题,解决根的存在及个数问题,并将函数的单调性与函数零点融入其中形成知识组块. APOS理论强调在数学教学中应该关注过程,教师要给学生抽象概括的机会,让学生从大量的事例中观察、分析、抽象概括出它们的本质属性.教学中应突出强调学生应经历一个从“形”到“数”的认识过程.由此达到深入把握数学内容的本质.在教学中教师重点在于促进学生的思考,设计出以知识的产生和发现的主线、并以知识产生的必要性与合理性为着力点,努力用问题引导实施教学.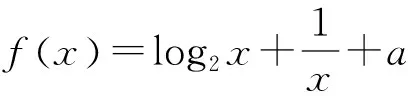
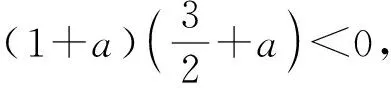


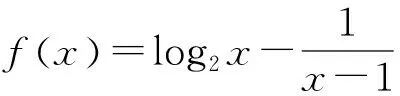
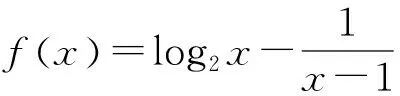
四、结语
