新型波形钢腹板组合梁桥车桥耦合振动仿真分析

2023-01-16余奋亿于海峰邱妍辉

广东公路交通 2022年6期

余奋亿，于海峰，邱妍辉

(1.广州通辉工程有限公司，广州 510640；2.广东交科检测有限公司，广州 510550)

0 引言

减轻桥梁上部结构自重一直是桥梁技术发展的重要课题之一。基于传统的钢-混组合梁桥，聂建国[1]等提出了一种新型的波形钢腹板组合桥梁结构，如图1所示。这种新型的组合桥梁可以有效减轻桥梁自重，充分发挥材料潜能，提髙桥梁的跨越能力。近年来，新型波形钢腹板组合梁桥得到了国内外众多研究学者的关注。

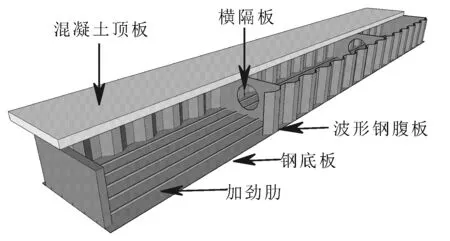
图1 新型波形钢腹板组合梁桥

波形钢腹板的弯曲性能、剪切性能、扭转性能、空间行为及动力性能是相关学者的研究热点之一。KOVESDI B[2]、刘梓锋[3]等研究了波形钢腹板组合梁桥的弯曲性能。PAPANGELIS J[4]、刘超[5]等针对波形钢腹板组合梁的抗剪性能进行了一系列研究。 PROKIC A[6]、张元海[7]等在波形钢腹板组合梁扭转性能方面做了大量工作。CHEN[8]、胡旭辉[9]等对波形钢腹板组合箱梁的剪力滞效应进行了深入研究。此外，在动力特性方面，国内学者也针对其弯曲振动、扭转振动及车致振动等进行了研究。胡霖远[10]等通过能量变分法分析各种边界条件下的波形钢腹板组合梁，导出波形钢腹板梁的频率方程，所得自振频率与有限元结果基本吻合。郑尚敏[11]等基于Hamilton原理推导了波形钢腹板扭转频率的解析解，并通过理论推导、试验验证和有限元相结合的方式，对波形钢腹板组合梁桥的自振频率展开了研究。邓露[12]等建立了车桥耦合振动程序，研究发现钢-混组合梁桥的极限承载力可靠度受到车致疲劳损伤的影响较大。

目前，针对该类新型波形钢腹板组合梁桥的车致动力效应的研究相对不多，基于此，本文以某跨径为30m的新型波形钢腹板组合梁桥为研究背景，运用ANSYS和UM软件建立ANSYS-UM联合车桥耦合仿真模型，分析了在单车工况、横向双车工况和纵向双车工况下桥梁的动力响应，并计算了桥梁在三种工况下的车致动力冲击系数。

1 车桥耦合振动仿真模型

1.1 路面不平整度模拟

路面不平整度通常作为车桥耦合振动主要的激励源之一[13]，直接影响到车桥耦合振动的动力响应。路面不平整度一般视为均值为零的高斯随机过程，其表达式可通过应用功率谱密度函数的傅里叶逆变换得到，如式(1)～式(2)所示。

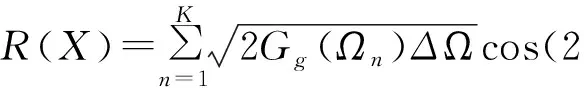
(1)

式中:X为桥梁纵向坐标；Ωn为离散采样点；ΔΩ为采样间距；k为采样数；θr为随机相位角。

Gq(Ω)=Gq(Ω0)(Ω/Ω0)-2Ωl≤Ω≤Ωu

(2)

式中：Ω为空间频率；Ωl为截止下限频率；Ωu为截止上限频率；Ω0为标准空间频率；Gq(Ω)为路面不平整度系数，其值根据路面状况确定。

根据路面状况良好程度和路面平整度功率谱密度值，ISO-8608标准将路面平整度划分为五个等级，分别为非常好(A)、好(B)、一般(C)、差(D)、非常差(E)。考虑路面平整度沿桥面横向变化，即车辆沿纵向行驶的路面平整度样本曲线不同，图2所示为C级平整度下车辆左、右车轮的平整度随机样本曲线。

图2 路面平整度样本曲线

1.2 车辆模型的建立

本文采用了更加符合实际情况的三轴车辆模型，该车辆模型的合理性在相关研究成果中已得到验证[14-15]。如图3所示，MC、JC和IC分别代表车体质量、俯仰惯量和侧倾惯量；Csi(i=1,2,…,6)和Ksi(i=1,2,…,6)表示车辆悬架阻尼和车辆悬架刚度；Mti(i=1,2,…,10)为轮胎质量；αC和βC分别为俯仰角位移和侧倾角位移；Zti(i=1,2,…,10)为轮胎位移；L1、L2和L3分别表示车体质心至前、中、后轴的距离；ZC表示车体的浮沉位移；b1表示悬架中心至车辆质心轴的距离；b2表示较近一侧轮胎至车辆质心轴的距离；b3表示较远一侧轮胎至车辆质心轴的距离。车辆的相关参数取值如表1所列。

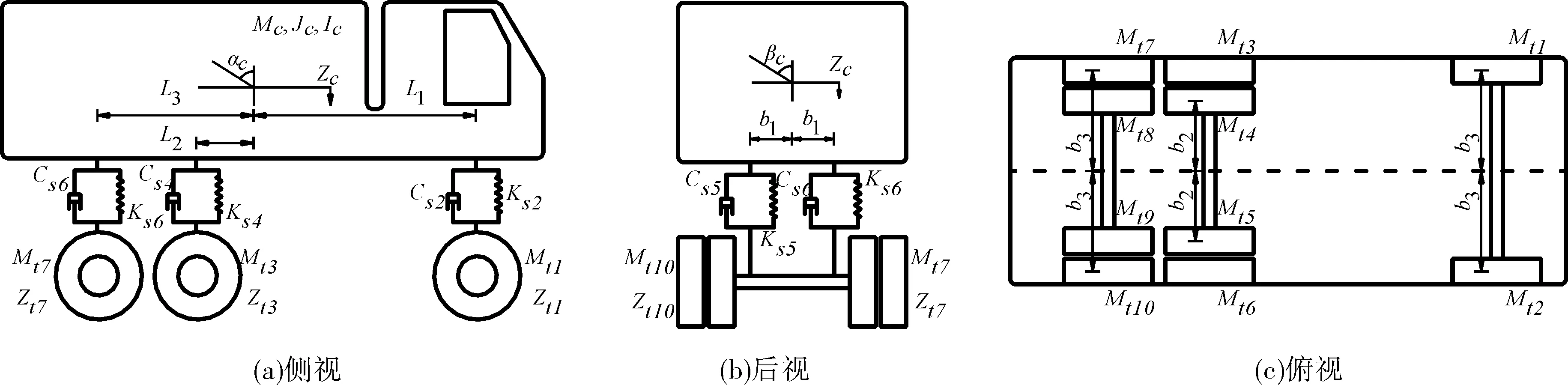
图3 车辆模型

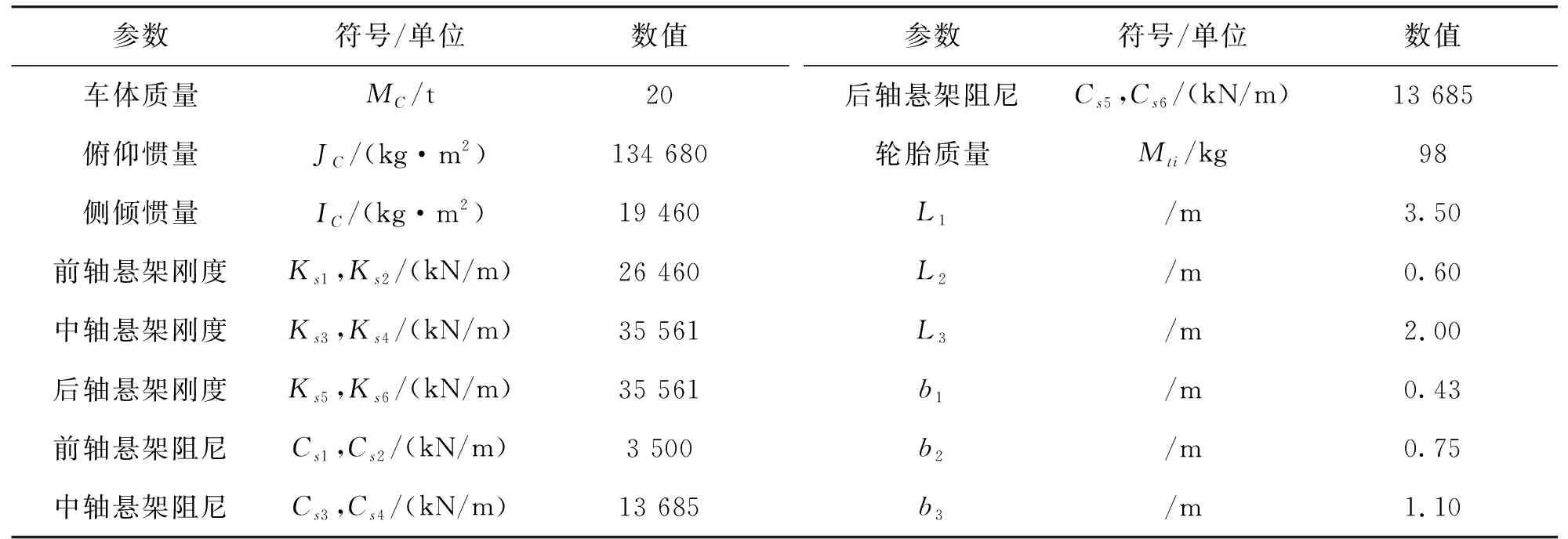
表1 车辆模型参数取值

车辆模型通过质量、弹簧和阻尼器模拟车辆的车体、悬挂和轮胎。通过Fiala轮胎模型模拟轮胎，车轮与桥面采用车轮圆盘模型，比单点接触模型具有更高的精度，能够准确地反映车辆在实际行驶过程中的动态特性[16]，如图4所示。

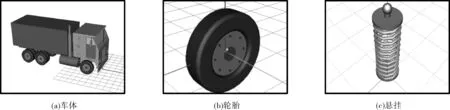
图4 车辆三维仿真模型

由达朗贝尔原理导出车辆的运动方程，表示为：

(3)

式中:Mv、Cv、Kv分别表示车辆的质量、阻尼和刚度矩阵；Dv表示车辆的位移矢量；Fvg表示由车辆自重引起的荷载矢量；Fvb表示轮胎变形引起的车桥相互作用力矢量。

1.3 桥梁模型的建立

本文的研究对象为某新型波形钢腹板组合简支梁桥，桥梁长30m、高1.5m，其横截面尺寸如图5所示。波形钢腹板采用的是BCSW1200型号，具体尺寸如图6所示。结构材料方面，混凝土为C50，钢材采用Q345C。混凝土和钢材的弹性模量分别为3.45×104MPa和2.06×105MPa，泊松比分别取0.2和0.3。

图5 桥梁横截面(单位：mm)

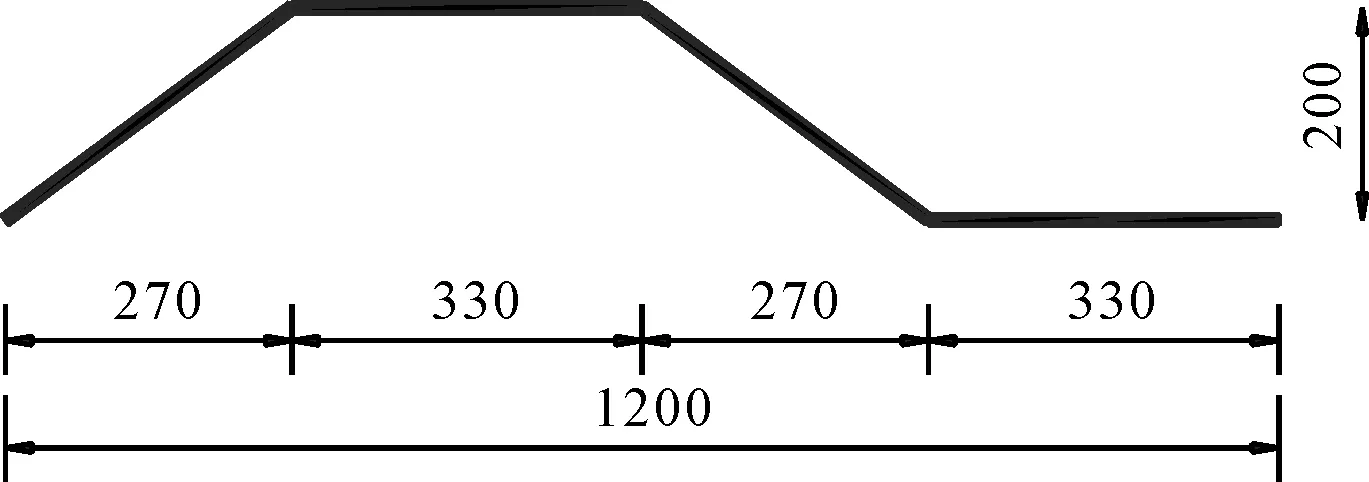
图6 波形钢腹板尺寸(单位：mm)

通过ANSYS软件构建桥梁的有限元模型，如图7(a)所示，其中混凝土和钢材分别采用SOLID45单元和SHELL63单元进行模拟。两种单元连接节点处通过节点耦合约束的方式建立刚性区域，全桥共建立节点52 575个，单元42 514个。通过ANSYS计算得到桥梁的第一阶弯曲自振频率为3.791Hz，一阶振型如图7(b)所示。

图7 有限元模型及振型

通过脉动法动力特性试验获取了桥梁实测自振特性，得到前三阶弯曲自振频率。桥梁现场试验状况如图8所示，功率谱密度如图9所示。

图8 现场数据采集

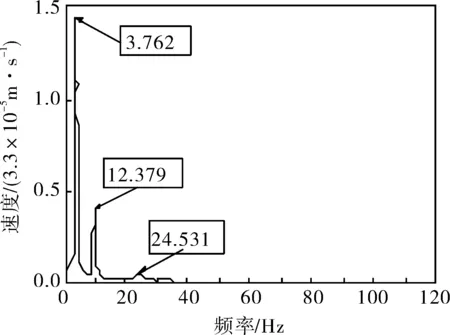
图9 功率谱密度

通过对比桥梁自振频率实测值与ANSYS计算值，验证所建有限元模型的准确性(表2)。结果表明，两者一阶弯曲自振频率的误差仅0.76%，数据吻合良好，有限元模型具有较高的准确性。

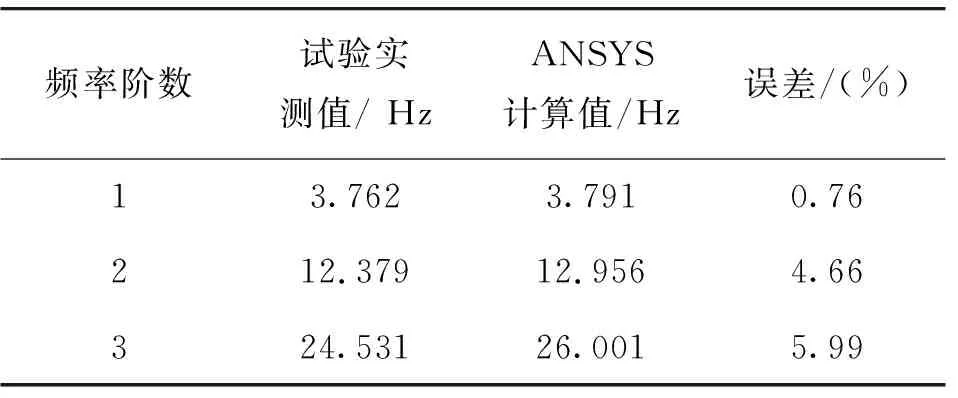
表2 弯曲自振频率实测值与ANSYS计算值对比

车辆荷载作用下桥梁结构的振动方程可表示为：

(4)

式中:Mb为桥梁的质量矩阵；Cb为桥梁的阻尼矩阵；Kb为桥梁的刚度矩阵；Db为桥梁的位移矢量；Fbv为车辆作用在桥面的作用力矢量。

1.4 车桥耦合模型的建立与验证

基于UM-ANSYS.exe接口程序将本文所建立的车辆模型和桥梁模型导入同一个UM仿真模型中，在UM软件中设置桥梁的约束节点，将车辆模型与桥梁模型进行耦合，得到车桥耦合振动仿真模型，如图10所示。为验证所建车桥耦合仿真模型的适用性，在ANSYS中也采用相同的车辆荷载进行多荷载步静力加载，获得桥梁静挠度计算值。通过对比UM计算值，表明数据吻合良好，误差为1.48%，验证了所建车桥耦合仿真模型的适用性(图11)。

图10 车桥耦合模型

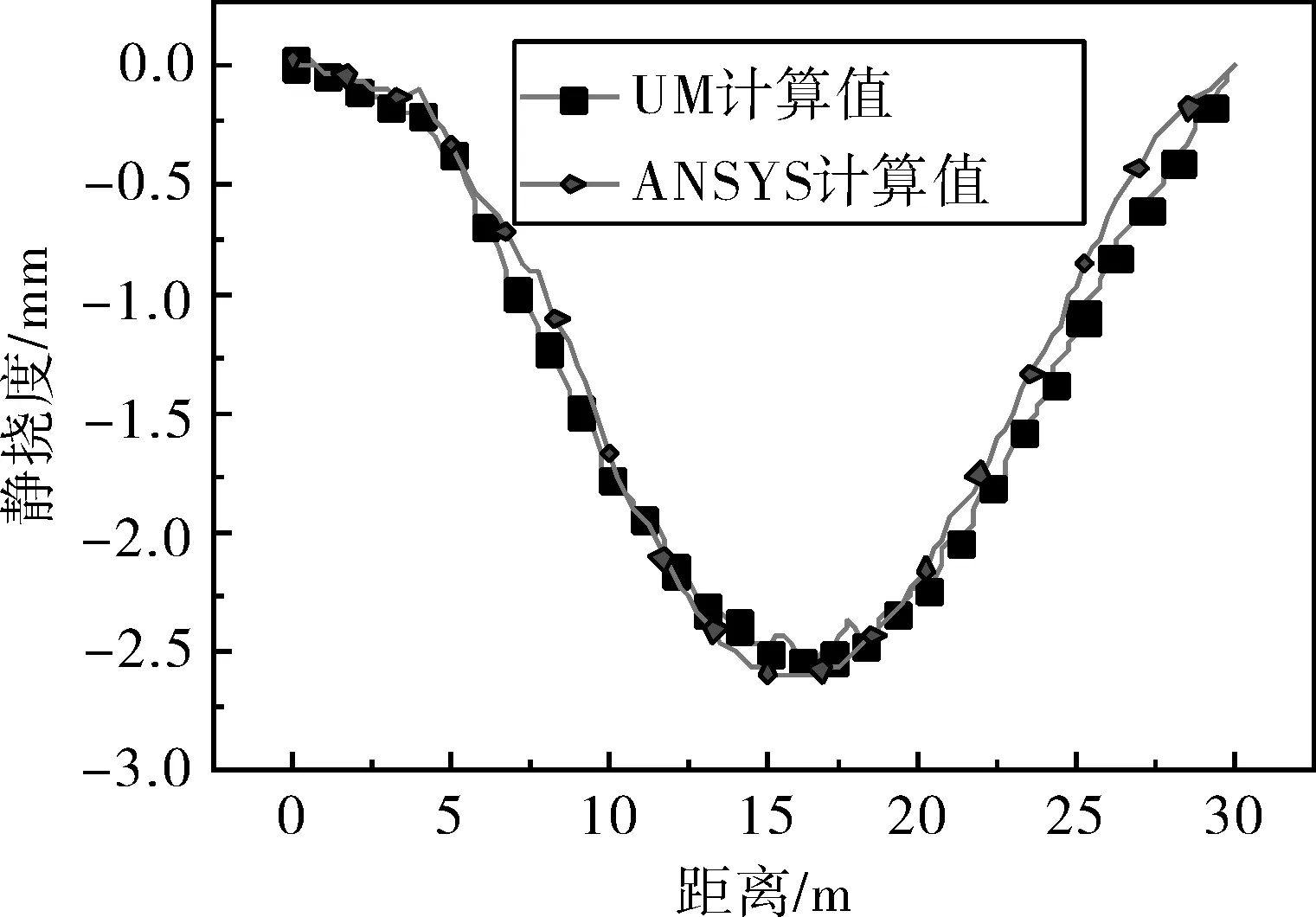
图11 UM和ANSYS静挠度计算值

根据车桥接触点的位移协调关系和相互作用力关系[18]，车辆桥梁刚柔耦合模型的振动方程可表示为：

(5)

式中:Cb-b、Cb-v、Cv-b、Kb-b、Kb-v、Kv-b、Kb-r、Kv-r为与时间相关的桥面和车轮的接触力；Fg为车辆重力。

本文所建立的车桥耦合振动方程采用固定界面模态综合法求解，剔除6个刚体模态。将高精度桥梁模型和车辆模型导入UM软件中，形成车桥耦合系统，UM软件通过Park积分法求解车桥耦合振动方程。这种新的求解方法在计算中忽略桥梁的高阶模态贡献，仅选取少量低阶模态参与计算，可大幅降低求解动力学方程的复杂程度[17]。

UM软件Simulation后处理程序具体的仿真流程如图12所示。

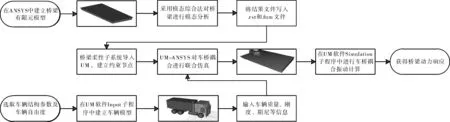
图12 车桥耦合振动仿真流程

2 数值分析

2.1 动力冲击系数

动力冲击系数是研究车辆对桥梁冲击作用的重要指标之一，众多学者对此进行了大量相关的研究，但在动力冲击系数的取值问题上仍未达成共识。动力冲击系数一般通过《公路桥涵设计通用规范》(JTGD60-2015)给出的以桥梁基频为参数的分段函数进行计算。实际上，车辆对桥梁的冲击作用不仅与桥梁基频有关，还与很多因素相关，如车辆重量、车辆行驶速度、路面平整度等。因此，基于车桥耦合振动理论研究多因素耦合作用下车辆对桥梁的冲击作用，具有重要的理论意义与实际意义。动力冲击系数的计算公式如式(6)所示。

(6)

式中:IM为冲击系数；ydm为车辆作用下桥梁的最大动响应；ysm为车辆作用下桥梁的最大静响应。

本文分别建立三座新型波形钢腹板组合梁桥的车桥耦合仿真模型，通过ANSYS和UM软件联合仿真计算三座桥梁在移动车辆荷载作用下的动力冲击系数，其基本参数见表3。

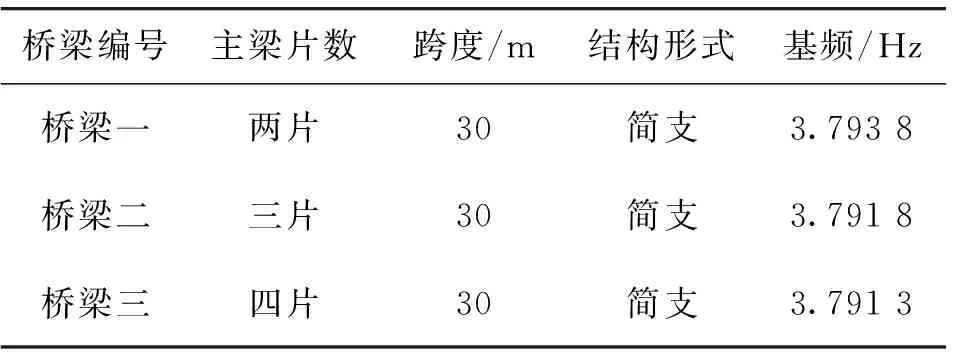
表3 三座桥梁的基本参数

2.2 单车工况下车桥耦合动力响应

为了研究单车工况下车速对新型波形钢腹板组合梁桥冲击系数的影响规律，考虑其他条件相同时，选择一辆三轴车行驶通过桥梁，进行车桥耦合仿真分析。

车辆加载位置均选择为三座桥梁最靠近纵向轴线的车道，考虑桥面平整度为C级，车重为20t，分析三轴车以速度为30km/h～120km/h范围、间隔为15km/h时匀速通过桥梁时动力响应的变化规律。

单车工况下，三轴车以不同速度行驶通过桥梁时的动力冲击系数见表4和图13所示。

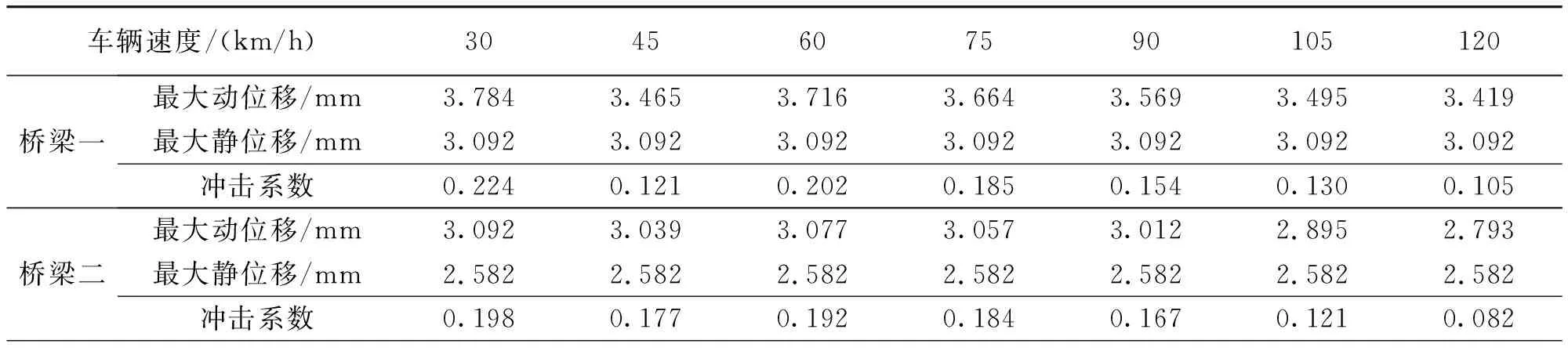
表4 单车工况下的动力冲击系数

(续表4)

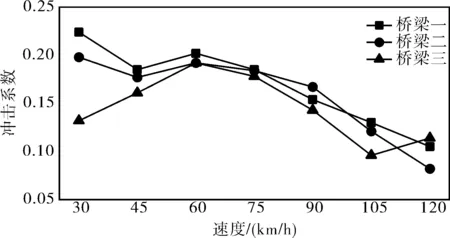
图13 单车工况下动力冲击系数变化曲线

由图13可以看出，桥面在C级平整度的情况下，随着车速的增加，三座桥梁的动力冲击系数随车速的增加均未表现出明显的单调变化趋势，而是整体波动的变化趋势。实际上，众多学者对于桥梁动力冲击系数随车速的变化规律尚没有一致的认识，有的认为是递增趋势、有的认为是递减趋势、还有的认为是波动趋势。

分析三座桥梁的变化趋势可大致发现：冲击系数最大值易出现在车速较低的时候，这可能是由于车速较低时车辆行驶时间更长，桥梁振动发展比较显著，高频波段得以充分发展，进而动力冲击作用较明显；冲击系数最小值易出现在车速较高的时候，因为车速越高时车辆在桥上行驶的时间越短，尤其对于中小桥梁来说，车辆行驶时间仅数秒，高频波段发展时长不足。因此，就小跨径桥梁而言，车辆行驶速度越高时，往往引起桥梁的动力响应反而较小，动力冲击作用不太明显。

2.3 横向双车工况下车桥耦合动力响应

为了研究横向双车行驶时车速对三座桥梁动力响应的影响，在其他条件相同的情况下，选择两辆相同的三轴车行驶通过桥梁，进行车桥耦合仿真分析。为了更加符合实际情况，考虑桥面平整度为C级，单车车重为20t，两车横向距离3.2m，分析两辆三轴车以速度30km/h～120km/h范围、间隔为15km/h时匀速通过桥梁引起的动力响应特性。

横向双车行驶工况下，两辆三轴车以不同的速度行驶通过桥梁时的动力冲击系数见表5和图14所示。

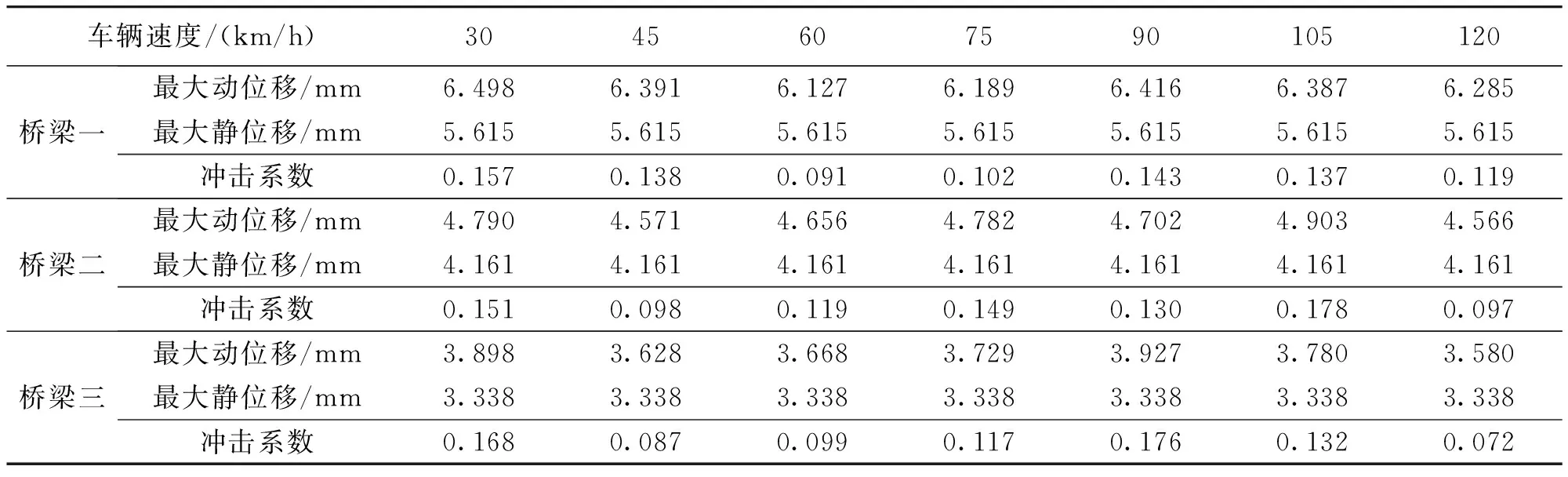
表5 横向双车工况下的动力冲击系数

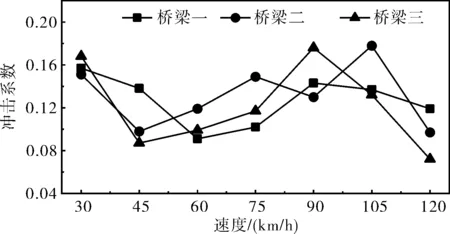
图14 横向双车工况下动力冲击系数变化曲线

从表5可以看出，相较于单车行驶工况，横向双车行驶会引起桥梁跨中截面更大的动挠度值，三座桥梁的最大动挠度值分别达到了6.498mm、4.903mm和3.927mm。由图14可以看出，桥面在C级平整度的情况下，随着车速的增加，三座桥梁的动力冲击系数随车速的增加仍呈波动变化的趋势。此外，在平整度等级为C级的情况下，三座桥梁的冲击系数均未超过规范设计值。

2.4 纵向双车工况下车桥耦合动力响应分析

为了研究纵向双车行驶时车速对三座桥梁冲击系数的影响规律，在其他条件相同时，考虑桥面平整度为C级，设置前车车尾至后车车头的距离为5m，分析两辆三轴车以速度为30km/h～120km/h范围、间隔为15km/h时匀速通过桥梁的动力响应特性。

纵向双车行驶工况下，两辆三轴车以不同的速度行驶通过桥梁时的动力冲击系数见表6和图15所示。

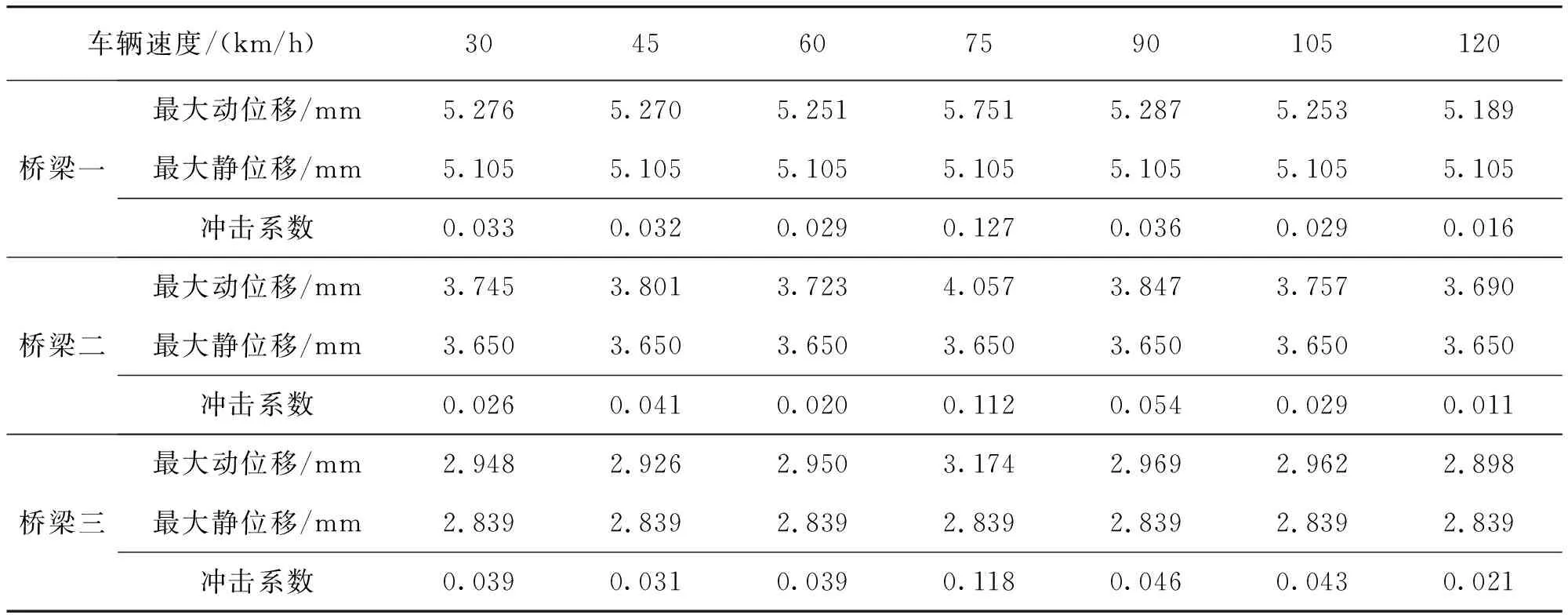
表6 纵向双车工况下的动力冲击系数

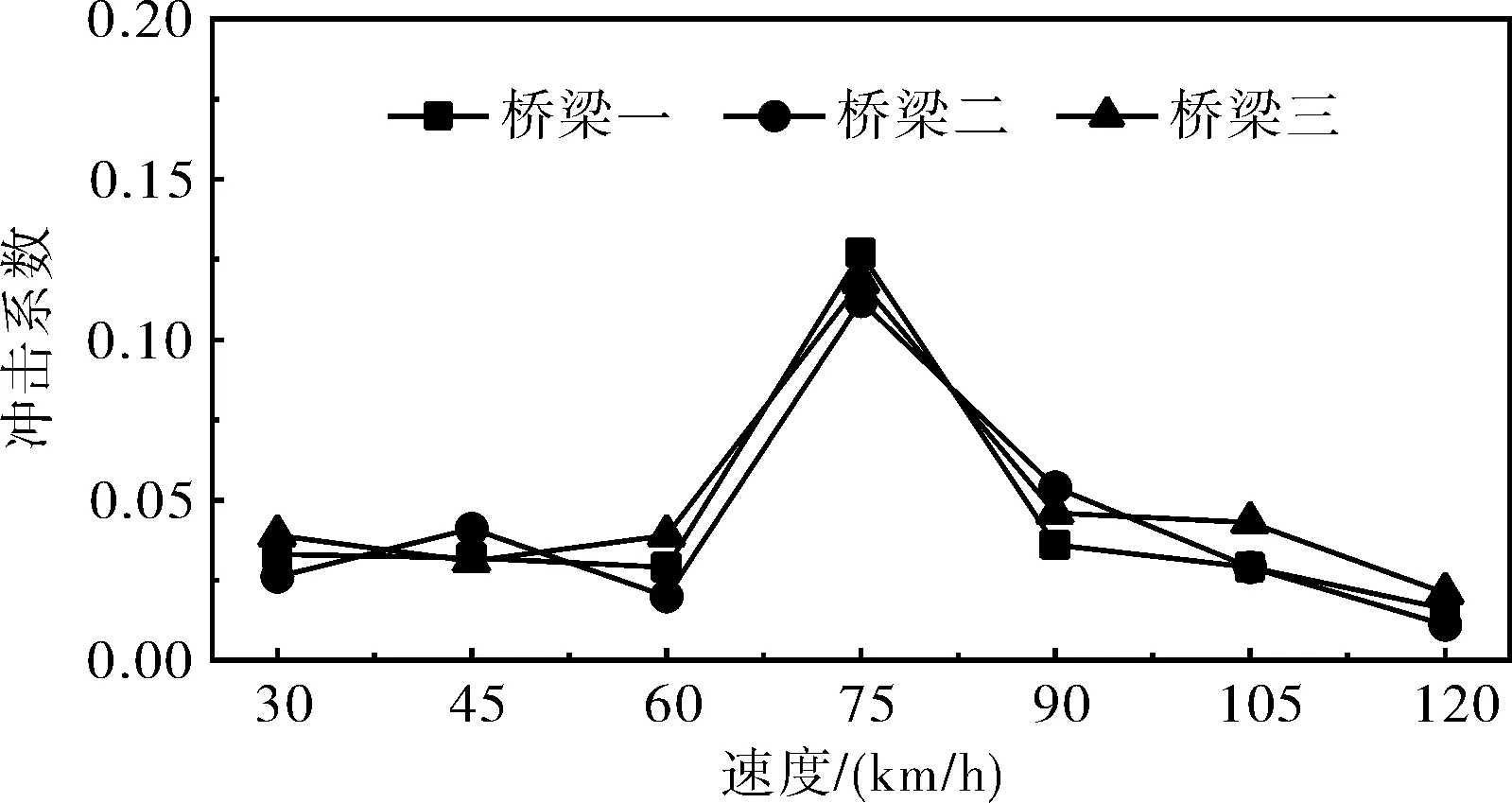
图15 纵向双车工况下动力冲击系数变化曲线

从图15可以看出，在纵向双车行驶工况下，三座桥梁的动力冲击系数随着车速的增加呈先增大后减小的变化规律。三座桥梁的冲击系数最大值均出现在速度为75km/h时，其最大值分别为0.127、0.112和0.118；三座桥梁的冲击系数最小值均出现在速度为120km/h时，其最小值分别为0.016、0.011和0.021。冲击系数最大值和最小值相差数倍，这仍然可能与车桥共振相关。

2.5 单车工况、横向双车工况和纵向双车工况比较

当桥面平整度等级为C级时，对三座桥梁在单车行驶工况、横向双车行驶工况和纵向双车行驶工况下的动力冲击系数进行对比，如图16～图18所示。

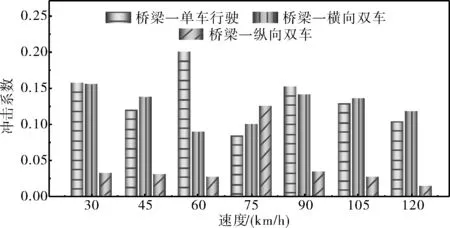
图16 桥梁一在三种工况下的动力冲击系数对比

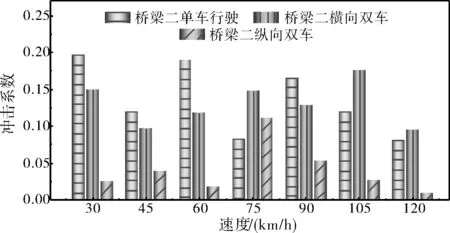
图17 桥梁二在三种工况下的动力冲击系数对比

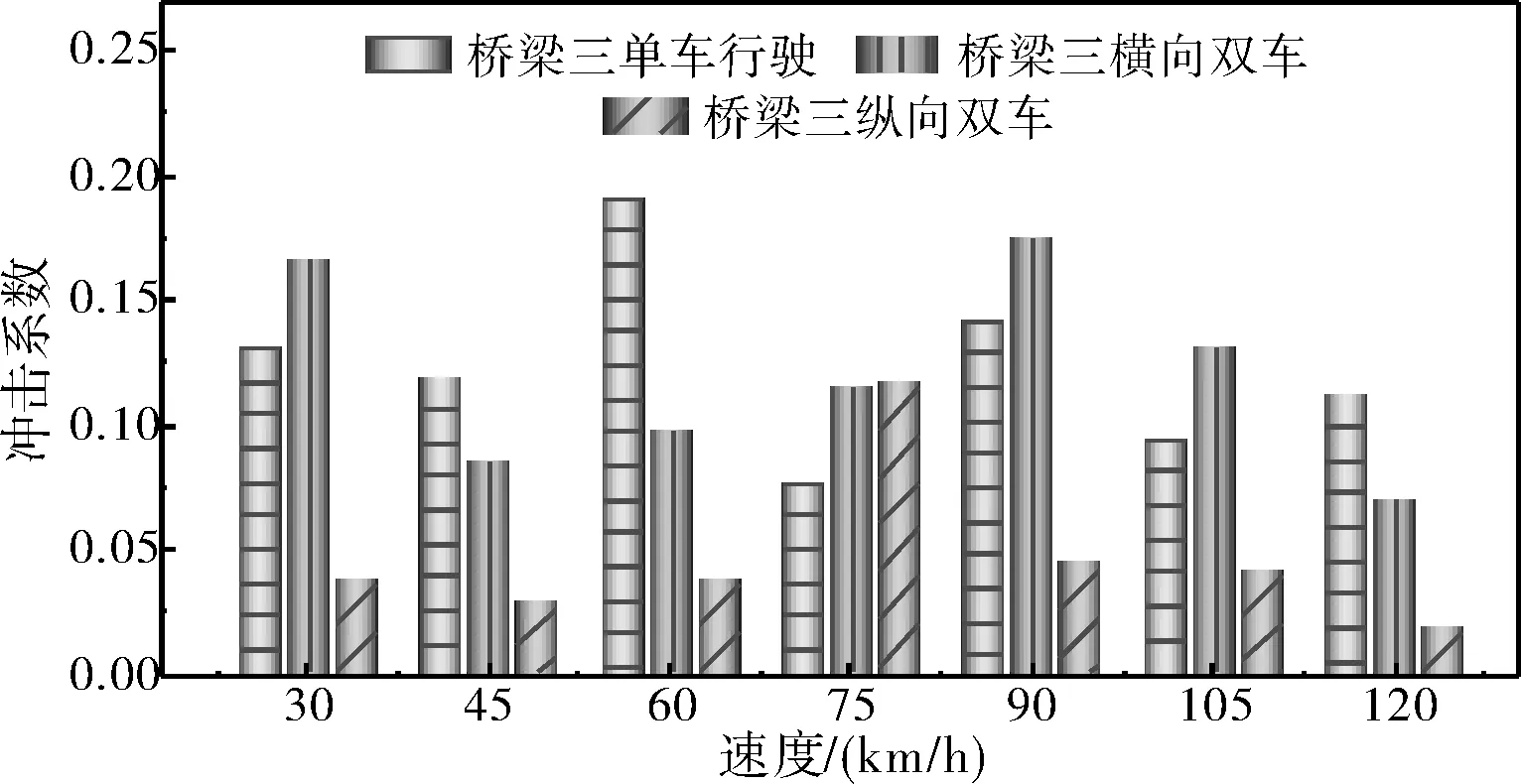
图18 桥梁三在三种工况下的动力冲击系数对比

由图16～图18可见，桥面在C级平整度的情况下，整体来看三座桥梁在纵向双车行驶工况下动力冲击系数均最小，在单车行驶工况和横向双车行驶工况下动力冲击系数均有可能最大。这可能是因为冲击系数不仅受到车辆荷载作用下桥梁的动效应影响，还与桥梁的静效应有关。因此，从桥梁动力冲击效应角度而言，当车辆数量较多时，可选择多车纵向排列行驶通过桥梁。