基于组合神经网络模型的金融时序预测

卜钰家

（澳门大学协同创新研究院，澳门 999078）

0 引言

股票价格预测是量化金融领域中的一个热门课题，如何利用这些股票市场中海量交易数据来预测股票价格成为了研究热点。以前研究股价预测问题时，常常选用的是单一模型，最开始使用ARIMA模型来进行股价预测［1-2］，真实数据中包含着线性信息和非线性信息，但ARIMA 模型更多地只利用信息中的线性部分。随着机器学习的发展，具有很好的非线性拟合能力的BP神经网络［3-4］和适合处理时间序列数据的LSTM 模型［5-6］也逐渐被应用在研究股价方面，学者也开始探究具有最好预测性的模型，但是单一的传统模型总是难以兼顾精度和效率［7-8］。

由于单一的模型不足以提取数据中的复杂关系，组合模型的概念开始被提出［9-10］。本文提出了BP-LSTM 模型和ARIMA-LSTM 模型，结合两种单一模型的优点，将数据中有效信息都描述出来，来提高预测结果的准确性。前者结合LSTM 模型处理时间序列的优点和BP 模型优秀的非线性映射能力和训练时间段的优点，后者结合LSTM 模型对非线性数据的极强处理能力和ARIMA模型有效提取数据中线性信息的能力。

1 模型基本原理

1.1 LSTM模型

LSTM 模型在循环神经网络的基础上进行改进，适用于从时间序列中提取时序特征，具有学习长期时间序列依存关系的能力。LSTM 模型主要规避了标准循环神经网络结构中梯度爆炸和梯度消失问题，在其基础上加入门控的概念，通过输入门、遗忘门和输出门对数据信息流动进行控制，因此，训练速度也会更快。

其中各个部分的解释如下：

（1）遗忘门ft：控制输入量和上一层隐藏层输出被遗忘的程度大小。

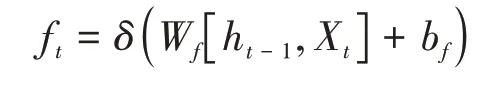
（2）输入门it：控制输入量和当前计算的状态更新到记忆单元的程度大小。

（3）输出门ot：决定需要输出的部分。

1.2 ARIMA模型

ARIMA 模型全称为差分整合移动平均自回归模型，是一种对时间序列数据进行分析和预测的算法模型。ARIMA模型预测原理可简括为：模型将时间序列数据默认为一组随机序列，使非平稳的数据经过差分后趋于平稳，转换为平稳的时间序列，并对以往数据间的线性关系构建模型，以预测数据未来值。

1.3 BP神经网络模型

BP 神经网络通常有三层或三层以上结构。BP 神经网络包括输入层、输出层，以及一个或多个隐含层。图2是一种三层BP神经网络结构。BP 神经网络采用梯度下降法，通过反向传播不断调整网络的权值和阈值，使网络的实际输出值和期望输出值之间的均方误差最小。其训练过程包括输入信号正向传播和误差信号反向传播。这两个过程循环进行，不断计算输出误差和调整权值，直到均方误差达到设定标准。

图1 LSTM模型的基本结构图

图2 BP神经网络模型的基本结构图

1.4 BP-LSTM模型

BP-LSTM 模型（见图3）是混合模型，分为两层，第一层采用BP 网络；第二层采用LSTM模型。BP 神经网络结构训练速度快，能提高预测效率，但在处理时间序列上精度不如LSTM模型，BP 模型接受训练集数据的输入，通过梯度下降算法不断修正权值和阈值，最后输出预测结果和预测残差，将残差输入到后端LSTM 模型中，LSTM 再对输入进行训练。可以提升网络的非线性映射能力，同时避免过度拟合。最后得到股票的最终预测值是BP 神经网络的预测值加上LSTM修正的残差值之和。

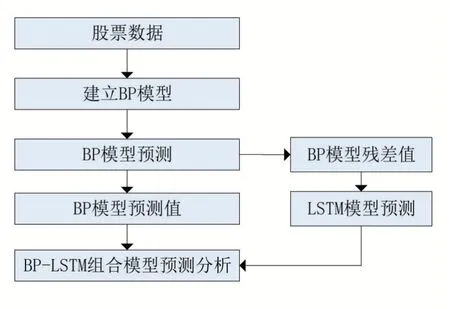
图3 BP-LSTM 组合模型的基本流程图

1.5 ARIMA-LSTM模型

ARIMA-LSTM 模型（见图4）是混合模型，分为两层，第一层采用ARIMA 网络；第二层采用LSTM 模型。ARIMA 模型只局限于预测数据的线性部分，而LSTM 神经网络模型更适合对数据的非线性部分信息进行提取，因此提出一种能够提取数据线性及非线性特点的ARIMALSTM 混合模型对复杂的股票数据进行拟合。其思想是：通过ARIMA 模型建模提取股票数据存在的线性关系，充分利用时间序列上数据间的关联性；根据自回归差分平均模型可知残差序列理应不呈现线性相关，因此进一步利用LSTM 神经网络模型训练修正残差序列，再将修正后的残差序列作为输出。最终结合ARIMA 模型预测的线性部分和LSTM 模型对残差的修正得到最终的股票预测值。

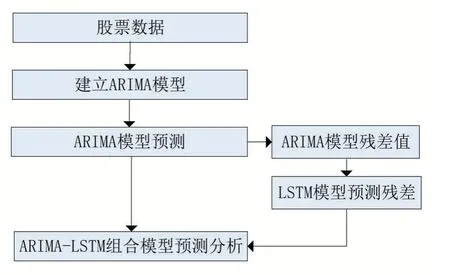
图4 ARIMA-LSTM 组合模型的基本流程图

2 数据表示和处理

2.1 数据集选择和特征选择

本文研究选择了上证指数2017年1月3日到2022年7月4日共计1336 条股票数据作为数据集，来进行训练和测试。将数据集的前80%作为训练集，后20%作为测试集，即2017年1月3日到2021年7月1日的数据为训练集，2021年7月2日到2022年7月4日的数据为测试集。本研究选择了8个股票交易数据，分别为最高价、最低价、开盘价、前收盘、涨跌额、涨跌幅、成交量和成交金额。

2.2 数据预处理

股票的各个交易指标具有不同的量纲和量纲单位，这容易影响数据分析的结果，为消除指标之间的量纲影响和提高模型的训练效率，需要对数据进行标准化处理。本文采用最大最小标准化的方式处理数据，标准化公式如式（1）所示：

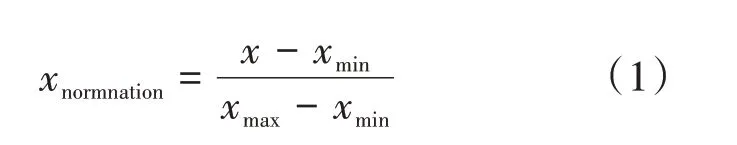
2.3 模型评估指标

为了更好地评估模型的预测结果，本文选择三个性能指标，均方误差（Mean Square Error，MSE）、平均绝对误差（Mean Absolute Error，MAE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE），来评估和对比模型的预测能力。MSE是真实值与预测值的差值的平方然后求和平均；MAE揭示误差绝对值的均值情况；MAPE是统计预测准确性的一种方法。以上三类误差均是数值越小表示模型预测效果越好。方程如下所示：

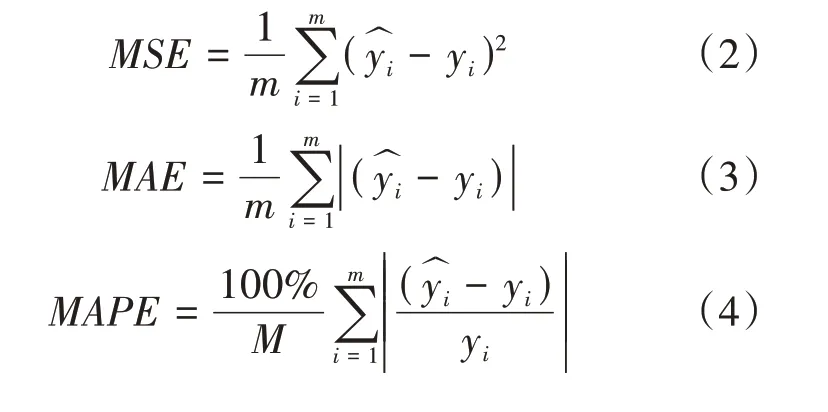
3 实证分析

本文使用Python 语言来编程，深度学习框架Tensorflow 为后台。组合神经网络模型，利用LSTM 优化预测残差，此处的LSTM 神经网络中引入Adam算法。

3.1 LSTM模型

图5为在测试集上用LSTM 模型预测的值和真实值的对比图。图5显示，LSTM 模型预测出的值和真实值有相似的整体趋势，能够反映出股价的局部变化。但可以看出预测值具有明显的滞后性，并且精度不高。

图5 LSTM模型真实值与预测值

3.2 BP神经网络模型

图6为在测试集上用BP 模型预测的值和真实值的对比图。图6显示，BP 模型预测效果不太好。但在局部的一些位置可以反映出股票的发展趋势，但是整体精度不够，当股价急剧变化时，不具有敏感性。模型不能准确地预测出股价，但是符合股价的基本走势，更适合用于预测股价的涨跌，而非具体的值。

图6 BP神经网络模型真实值与预测值

3.3 构建ARIMA模型

图7和图8分别为上证指数的收盘价时序图和一阶差分图。

图8 上证指数的收盘价的一阶差分图

根据一阶差分后股价序列的自相关和偏自相关图，选取可能的ARIMA 模型进行参数显著性、模型显著性检验，选出针对上证指数的最优模型——ARIMA（2，1，5）。图9为在测试集上，用ARIMA（2，1，5）模型预测的值和真实值的对比图。图9显示ARIMA（2，1，5）模型拟合结果与真实值高度接近。但存在滞后性的问题，并且在局部预测精度偏低。

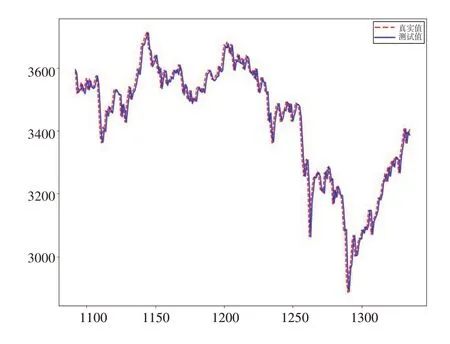
图9 ARIMA（2，1，5）神经网络模型真实值与预测值

3.4 构建BP-LSTM模型

图10为在测试集上用BP-LSTM 模型预测的值和真实值的对比图。图10显示，BP-LSTM 模型在一些峰值处呈现较大的误差，说明BPLSTM 模型对于一些急剧变化过于敏感。但可以看出BP-LSTM模型预测效果优于BP模型，首先BP-LSTM 模型的预测值更加贴近真实值，且预测值的走势更符合真实值。

图10 BP-LSTM 组合模型的真实值与预测值

3.5 构建ARIMA-LSTM模型

图11为在测试集上用ARIMA-LSTM 模型预测的值和真实值的对比图。图11显示，ARIMALSTM 模型预测效果优于单一模型，结合了两个模型的优点，首先ARIMA-LSTM 模型的滞后性优于ARIMA 模型，而且预测值更贴合真实值，这一点优于LSTM模型。

图11 ARIMA-LSTM 组合模型的真实值与预测值

4 实验评估

综合对比以上五个模型的预测值和真实值的差异，可以得出ARIMA-LSTM 模型的预测效果最好，其次是ARIMA 模型，LSTM 模型，BPLSTM 模型，BP模型最差。

由表1可知，这五种模型中ARIMA-BP 模型的MSE 和MAE 最小，说明在本文所选的数据集上ARIMA-LSTM 模型的预测效果最好，而BP模型的预测效果最差。对比BP 模型、BP-LSTM模型、ARIMA 模型和ARIMA-LSTM 模型可知，单一模型的预测效果没有多模型组合的预测效果好，可能是因为单一模型对数据的有效性较低。ARIMA-LSTM 模型的MAPE 值最低，说明这个模型具有不错的预测能力。

表1 不同模型的评论指标

5 结语

本文选取了上证指数的1336 条数据，通过建立LSTM、BP、ARIMA、BP-LSTM、ARIMALSTM 这五种神经网络模型，利用Python 语言实现对应算法，对数据集进行训练分析和对比，探索组合神经网络模型是否优于单一模型。从两个方面来建立组合神经网络模型，BP-LSTM模型结合BP 网络预测时间短和LSTM 模型精度高的优点，利用BP 模型提取数据中的非时序信息，再用LSTM 模型提取数据中的时序信息。ARIMA-LSTM 模型结合ARIMA 模型有效读取数据中线性信息和LSTM 适合提取数据中非线性信息的优点。提出的两种组合模型都是希望更高效地提取数据中的信息，实现更有效的预测，同时也是对股价预测的新的探索。本文得出ARIMA-LSTM 组合神经网络模型优于单一模型，减少滞后性，同时在股价预测方面具有更高的准确度。BP-LSTM 组合模型优于BP 模型，能预测股市的大概走势，但是准确性并不高，并且在峰值处容易过度预测，更适合来做股价涨跌的预测。