混合不完备数据的新型双邻域粗糙集分类方法

黄恒秋，陈素霞，翁世洲

（1.广西民族师范学院数理与电子信息工程学院，崇左 532200；2.河南轻工职业学院计算机与艺术设计系，郑州 450052；3.广西民族师范学院经济管理学院，崇左 532200）

0 引言

经典粗糙集模型以等价关系作为基本近似单元，要求数据集为离散型，然而现实中大部分数据以数值型或者混合型存在。Lin［1］首次用邻域关系代替经典的等价关系，构建了邻域粗糙集模型。Hu 等［2］采用距离函数定义邻域关系，使其能够直接处理离散型和数值型数据，进一步拓展了邻域粗糙集模型的研究内容及应用范围。

邻域粗糙集模型主要应用于属性约简和基于决策规则的分类［3］，目前已经取得了丰硕的研究成果，比如基于邻域粗糙集属性约简和经典分类方法融合的混合分类方法［4-9］；基于邻域决策粗糙集和三支邻域决策粗糙集的分类方法［10-11］；基于邻域粗糙集约简规则的最近邻分类方法［12-15］。

基于邻域粗糙集约简规则的分类方法，由于容易理解和方便实现，同时能够充分利用邻域的局部最优决策信息［8］，目前已获得了广泛应用［7］，但是针对现实中广泛存在的含离散属性、数值属性和缺失值的混合不完备数据集研究并不多见。目前，针对该类数据集主要有以下几种处理方法：①使用能容忍缺失值的距离函数，比如混合距离HEOM［16］，该函数对属性的缺失值用其最大值来代替，称为最乐观的情况。文献［17］指出，如果属性较多，同时缺失比例也较大时，HEOM 距离容易造成数据集失真。文献［18］在使用HEOM 时，针对缺失值则是使用最小值来代替，即最悲观的情况。②对邻域关系进行拓展定义，使其成为邻域容差关系，比如视缺失值与其他非缺失值都相等的邻域容差关系［19-20］，而文献［21］则从两个样本之间的联系度出发，通过定义三种联系度指标，给出邻域联系度容差关系。③将联系度系数转化为距离，从而方便计算和拓展应用到其他模型［22-23］。该方法避免了对缺失值的填充，同时又较好地利用了联系度信息，很好地对不确定样本相似性进行了有效度量。针对混合不完备数据集，文献［24］给出了基于邻域联系度转化为计算距离的双邻域粗糙集分类方法，也取得了优异的分类效果，但是该距离函数（文献中称为邻域联系度距离）有三个参数需要通过大量实验来确定，限制了其拓展应用。

本文在文献［24］的基础上，首先对其邻域联系度距离进行拓展定义，提出一个不带参数的邻域联系度距离函数；其次构建基于邻域联系度距离的新型双邻域粗糙集模型；最后给出基于覆盖约简的新型双邻域粗糙集规则学习与分类算法。

为了验证本文给出的分类方法的效果，选取7 个UCI 数据集进行了对比实验，通过与HEOM 距离取最大值、HEOM 距离取最小值、文献［24］的结果进行对比，结果表明本文提出的分类方法仍然取得了优异的分类效果。

1 邻域粗糙集相关概念

1.1 邻域关系

定义1［2］给定数据集构成的决策系统I=(U,A⋃D,V,f),B⊆A,定义B上的δ-邻域关系为

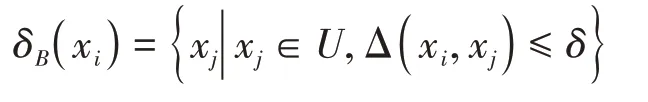
这里δ≥0，Δ是为距离函数。

定义2［19］设I=(U,A⋃D,V,f)为混合不完备系统，B⊆A,B=BC⋃BN,BC记为离散属性，BN记为数值属性，δ≥0。定义B的邻域容差关系为

其中箭头符号（→）表示关系满足的条件，星号（*）表示属性取值为缺失值。

定义3［21］对于混合不完备系统I=(U,A⋃D,V,f),|A|=N,Δ 表示绝对值距离，(xi,xj)∈U2为集对。记ε为相容邻域半径，M={a∈A|Δa(xi,xj)≤ε} 为集对取值在ε内的属性集；H={a∈A|Δa(xi,xj)＞ε} 为集对取值在ε外的属性集合；G={a∈A|f(xi,a)=* ∨f(xj,a)=*} 为集对中属性取值存在缺失值的属性集。记m=|M|N,g=|G|N,h=|H|N，则集对(xi,xj)的邻域联系度为

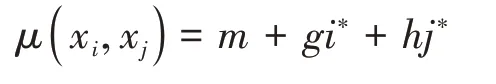
这里m、g、h为同一度、差异度和对立度；i*、j*为用于区分差异度和对立度标识。取0 ≤t≤1,B⊆A,则B上的邻域联系度容差关系为

定义4［15］记样本xi的Tri-分割邻域为

这里Δ 为距离函数；β为异质度，即邻域中与xi不同类别样本数量的占比；δβ是异质度为β时的邻域半径。则Tri-分割邻域的下、上近似邻域定义为

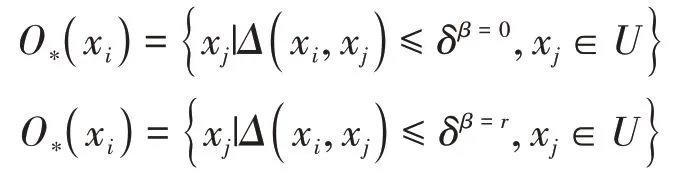
下近似邻域要求β=0，上近似邻域要求β=r，r∈(0,1) 。通过邻域异质度，可以控制邻域样本的类别纯度，一般情况下纯度越高，决策能力越强。区别于一般的邻域粗糙集模型只用一个半径来定义近似邻域，这里的上、下近似邻域半径是不相同的，他们通过邻域异质度来控制，称为双邻域近似。

1.2 邻域系统中的距离度量

定义5闵氏距离［2］

这里m表示属性维度。p=1 时表示闵可夫斯基距离；p=2时表示欧氏距离；p=∞时表示切比雪夫距离。

定义6混合距离［17］

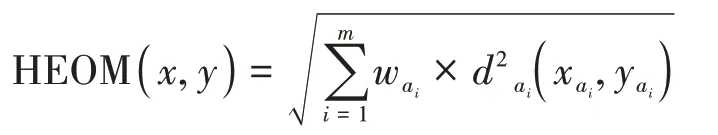
这里：

定义7［24］给定两个样本构成的集对(x,y)，其邻域联系度为μ(x,y)=m+gi*+hj*,则它们的邻域联系度距离定义为

这里w1,w2,w3为同一度、差异度和对立度的惩罚系数，且满足w1+w2+w3=1。

2 基于无参数邻域联系度距离的新型双邻域粗糙集模型

2.1 无参数邻域联系度距离

定义8给定样本(x,y)构成的集对(x,y)，其邻域联系度μ(x,y)=m+gi*+hj*,则无参数邻域联系度距离定义为

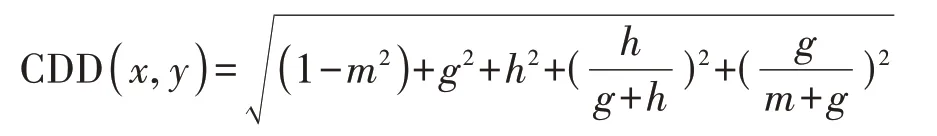
定义8 是对定义7 的拓展，该邻域联系度距离函数不带参数，与定义7 相比还多了后面两项，表示两个样本偏向对立面的程度，即差异度和对立度的转化度量。

2.2 新型双邻域粗糙集模型

定义9给定混合值不完备数据集构成的决策系统I=(U,A⋃D,V,f),B⊆A，记B上关于样本xi∈U的β-划分邻域为

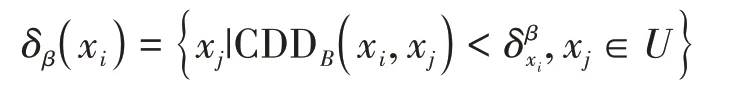
其中CDD 为无参数邻域联系度距离函数；β∈[ 0,1) 为异质度，即邻域样本中与xi不同类别的样本数量占比；是异质度为β时样本xi的邻域半径，则xi基于β-划分邻域的上、下近似邻域定义为

其中下近似邻域半径=CDD(xi,NM(xi))-(CDD(xi,HM(xi))+η),上近似邻域半径=CDD(xi,FM(xi)),NM(xi)为到xi的最近不同类样本，HM(xi)为到xi的最近同类样本，FM(xi)是使xi的邻域异质度为r且邻域样本数量最大的样本，r∈(0,1) ；η为调整系数，文中取η=0.0001,是对最近同类样本与最近异类样本距离相同时的调整。

定义10给定混合不完备数据集样本构成的论域U,

分别称为下近似邻域粒度集和上近似邻域粒度集，并记(U,N*)和(U,N*)为下、上近似邻域空间。

定义11对X⊆U,则X的下近似和上近似分别定义为

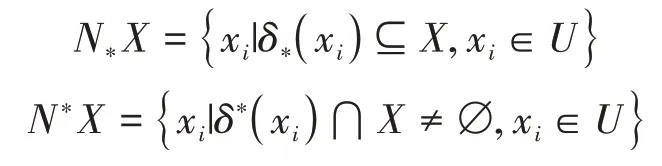
定义12称(N*X,N*X)为X的新型双邻域粗糙集。

3 基于无参数邻域联系度距离的新型双邻域粗糙集规则约简方法

定义13［14］记C={δ(x1),δ(x2),…,δ(xn)}为论域U的点覆盖，则称U,C为邻域覆盖空间，U,C,D则称为邻域覆盖决策系统。

定义14［14］U,C,D为邻域覆盖决策系统，Xi为决策类，如果∃δ(x'i)∈C,使得δ(x'i)⊆δ(xi)⊆Xi则称δ(x'i)对于Xi是可约的，否则是不可约的。

定义15［14］给定U,C,D，对于任意决策类Xi，都不存在δ(x'i)∈C使得δ(x'i)⊆δ(xi)⊆Xi，则称U,C,D是不可约的，否是可约的。

定义16［14］U,C,D为邻域覆盖决策系统，C'⊆C为去掉冗余覆盖后得到的一个新的覆盖，且U,C',D不可约，则称C'是C的相对约简。

定义13—定义16 介绍了基于覆盖约简的粗糙集规则约简理论，本文基于该理论给出新型双邻域粗糙集规则约简方法。

算法1新型双邻域粗糙集规则约简算法

输入：I=(U,A⋃D,V,f);

输出：约简后的下、上近似规则集R1和R2Step1: 对∀xi∈U构造{δ*(xi),δ*(xi)},计算和，同时计算上、下近似邻域的样本数量，并按降序排序。

Step2：∅→R1和∅→R2，并设C*=⋃{δ*(xi)}和C*=⋃{δ*(xi)}

Step3:执行以下操作，获得R1。

ifC*=∅，则输出R1

else 记

则R1⋃(xk,,dk)→R1，这里dk表示xk的类别。if∃δ*(xp)∈C*使得δ*(xp)⊆δ*(xk)，则∅→δ*(xp)，end，∅→δ*(xk)

end

Step4：执行以下操作，获得R2。

ifC*=∅，则输出R2

else 记

则R2⋃(xk,,dk)→R2，这里dk表示xk的类别。if ∃δ*(xp)∈C*使得δ*(xp)⊆δ*(xk)，则∅→δ*(xp)，end,∅→δ*(xk)

end

4 基于无参数邻域联系度距离的新型双邻域粗糙集规则最近邻分类方法

算法1 获得了新型双邻域粗糙集约简后的下、上近似规则集R1和R2，下面基于最近邻思想，给出新型双邻域粗糙集规则的最近邻分类方法。

算法2新型双邻域粗糙集规则最近邻分类算法

输入：测试集Test={x1,x2,…,xm}和R1,R2;

输出：测试集对应的分类结果。

Step1：针对每个xi∈Test，计算它到下近似规则集(xj,,dj)和上近似规则(xt,,dt)的无参数邻域联系度距离CDD(xi,xj)和CDD(xi,xt)

其中：j=1,2,…,|R1|,t=1,2,…,|R2|.

Step2：执行以下步骤获得xi的类别：

if ∃k使得CDD(xi,xk)≤，则xi的类别为dk(1 ≤k≤|R1|)

else if ∃l使得CDD(xi,xl)≤，则将所有的(xl,,dl)加入到候选集OC中。记OC中到xi的距离最小的规则是(xk,,dk)，则xi的类别为dk(1 ≤l≤|R2|)

else记

Δ(xk)=min{CDD(xi,xj)-}，则xi的类别为dk(1 ≤j≤|R1|)

end

5 实验分析

从美国加州大学公开的公共测试数据集（简称UCI数据集）中下载7个数据集作为实验数据，具体信息见表1。

表1 实验数据集描述

表1的7 个数据集中只有Heart 不含缺失值，其他6个数据集均存在不同程度的缺失。数据集的类别标签有两类和多类，属性类型有单纯的数值属性和离散属性，也有同时存在数值和离散两种类型的混合属性。因此，实验选取的数据集具有广泛性和代表性。

基于Matlab 2011B 进行编程实验。针对数值属性值，采用极差法标准化为［0，1］之间，离散属性则不做标准化处理。通过10 次交叉检验法计算实验分类精度。新型双邻域粗糙集模型近似邻域半径依据定义9的公式计算，并且邻域异质度r=0.05。

由于数值属性值全部标准化为［0，1］之间，而离散属性虽然属于分类型变量，但是取值均为整数。数值型属性值之间的差在［0，1］之间，离散型属性值之间的差要么等于0，即相似的情形；要么大于等于1，即相异的情形。因此相容邻域半径ε的值在（0，1）区间内选取，不管是离散属性还是数值属性都是适用的。本文中ε取值区间为［0.05，0.3］，间隔为0.05，取10次交叉检验分类精度的最优值进行比较，相关实验对比结果如表2所示。

表2 几种距离函数分类精度对比实验结果

其中HEOMA 和HEOMB 分别为混合距离HEOM 中缺失值用最悲观值0 和最乐观值1 来代替的两种形式。文献［24］的距离函数为带参数的邻域联系度距离，本文的是不带参数的邻域联系度距离。通过表2可以看出，缺失比例小于1%的4 个数据集，他们的分类效果相差不大。在缺失比例介于5.63%～9.78%的3个数据集中，文献［24］的方法略优于HEOMA 距离，相对于HEOMB 距离来说，则具有显著优势。本文的方法，无论是缺失比例小于1%的数据集，还是缺失比例在5.63%～9.78%之间的数据集，总体上分类效果与文献［24］的方法相当。值得说明的是，文献［24］定义的邻域联系度距离函数存在3个参数，需要通过大量的实验才能确定，在应用中会受到相当大的影响。本文方法对文献［24］的函数进行了拓展定义，给出了无参数的邻域联系度距离函数定义，其显著的优势就是不再需要通过大量实验去确定这些参数取值，极大拓展了其应用范围。

6 结语

本文给出了一种新型的双邻域粗糙集分类方法。该方法的显著特点是通过定义一个无参数的邻域联系度距离代替了原来带参数的邻域联系度距离。在分类效果方面与原来带参数的相当，然而原来带参数的邻域联系度距离需要通过大量实验来确定参数值，在实际应用中受到极大限制，这也是本文分类方法的优势和创新所在。将无参数邻域联系度距离函数应用于更多的数据挖掘与分析模型，拓展其应用场景，将是一个非常有意义的工作，也是我们下一步计划的研究和拓展方向。