以等效法为例谈高中物理教学中迁移思维的培养

徐海菊

（江苏省南通中学，江苏 南通 226001）

迁移思维是学生将已有的经验和能力迁移运用于后续问题研究中，由此促使他们完成对已有知识体系的重组，达成新认知体系的建构.就物理教学而言，学生在课堂上所接触的物理情境是有限的，当他们将视野转移到大千世界，复杂多变的情境让人眼花缭乱，学生要运用所学的物理知识来解决这些问题就需要充分运用迁移思维.在诸多物理问题的处理过程中，等效法有着广泛的用途.这也正是迁移思维的重要体现.教师在指导学生运用等效法分析问题时要关注学生迁移思维的培养.

1 对基础知识的掌握是发展迁移思维的基础

迁移思维依赖学生对基础知识的熟练掌握.学生只有对物理知识形成较为深刻的认识，他们才会娴熟地调用相关知识储备和经验来完成问题的分析和处理.在运用等效法处理问题时也同样如此，学生会将陌生的问题等效为他们所熟悉的情境来分析和处理，因此在日常教学过程中教师要关注学生对基础知识的掌握.

认知心理学指引下的高中物理强调，教师不能局限于对学生传输过多的间接经验，我们要让学生真正经历知识的形成过程，有效促进学生知识的内化建构.皮亚杰指出，当学习者的思维将现实场景和本质内容发生同化，且已有认知结构能够有效顺应对应的新情境，他们的思维将对特定现实产生适应.因此，为了促进学生迁移思维的发展，教师要研究学生的已有认知体系，让学生找到等效法运用的切入点，要让学生能够在等效处理中感受到概念的相似性.

例1.现有半球形导体材料，接成如图1所示甲、乙两种形式，则两种接法的电阻之比R甲∶R乙为

图1

（A）1∶1.

（B）1∶2.

（C）2∶1.

（D）1∶4.

等效法的使用将复杂的现象和过程转化为学生所熟知的结构，有助于学生问题解决效率的提升.在具体使用时，它需要学生对基本知识有着较为深刻的认知.只有这样，学生才能及时将相关内容有效迁移过来.

2 模型意识的培养有助于学生迁移思维的发展

在高中物理学习过程中，学生将遇到很多典型的物理问题和情境.对这些情境进行提炼，学生可以从中找到很多典型的模型，进一步研究，可找到一类问题的处理.这有助于学生理性思维习惯的养成.当学生遇到一些新的问题时，他们必然会将其与已经熟知模型进行比较，通过对比，他们会找到问题解决的突破口.

例2.如图2（a）所示，把轻质导线圈用绝缘细线悬挂在磁铁N极附近，磁铁的轴线穿过线圈的圆心且垂直于线圈平面.当线圈中通入图示方向的电流时，判断导电线圈如何运动.

图2

解析：这个问题考查的是导电线圈所受安培力的情形，具体情境比较复杂，因为线圈本身是一个圆形，不同位置所处的磁场环境还存在差异，分析时需要学生灵活运用微元和叠加的思想，抽象性很高.如果学生有着较强的模型意识，他们的处理将更加简单，问题中的环形电流可以视为如图2（b）所示小磁针，用安培定则，可以判断小磁针的S极针对条形磁铁，根据异名磁极相互吸引的结论，学生可以得到结果：线圈要向左摆.

3 通过比较强化迁移思维的培养

在物理问题的分析过程中，经常有这样的情况，多种方法能够殊途同归.在实际教学中，我们要让学生在比较中发现方法之间的关联，从中探索知识体系或思维方法之间的关联之处.这对学生迁移思维的培养有着重要的强化效果.

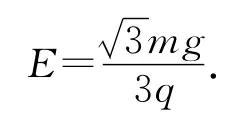
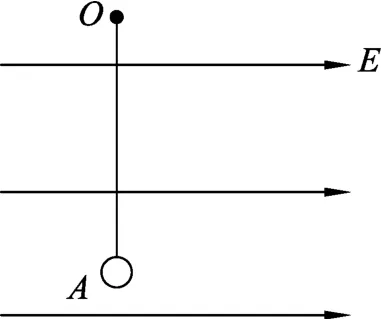
图3

这个问题的常规处理方法是对过程进行分析，即小球由静止释放后，它将以何种方式运动，受力分析是关键.分析可得小球受电场力、拉力和重力这3个力的作用，其中电场力和重力做功，小球先加速后减速，在达到其所能达到的最高点时，它的速度恰好等于0.可以假设摆到最高点时绳子与竖直方向的夹角为α，根据动能定理建立方程－mgr（1－cosα）＋q Er sinα＝0，代入电场强度与重力的关系，可以解得α＝60°.

对这个问题适当变换，采用等效法也可以让问题得到解决：重力和电场力都是恒力，其合力F是一个与竖直方向夹角为30°的恒力.将这个力视为等效重力，如果将绳子在原状态的基础上逆时针转动30°，并将小球在该位置无初速释放，小球能处于静止状态，该位置为等效最低点.回到原问题，如果小球从A点释放，则它能够摆到关于等效最低点对称的位置，即摆过角度为60°.

上述两种方法都能有效解决问题，教学中，我们鼓励学生多角度思考问题，并能够围绕这些不同的解题思路展开比较，以此来强化迁移思维的培养.处理例3时，采用动能定理，是将能量的观点迁移过来解决问题，采用等效法则具有一定的灵活性，需要学生能够将重力场中的运动情境迁移过来.这样的处理还有一定的延展性，比如可以继续提出问题：将小球由A点无初速释放，它在哪个位置具有最大速度？并求得最大速度为多少.用等效重力的视角来思考这个问题将更加简单，即小球在等效最低点有最大速度.在最大速度取值的具体求解中，学生可以采用动能定理进行表述，如此书写的答案更加清晰，因此在实际问题分析中，我们提倡学生多视角分析问题，将多种方法整合起来处理，这样可让问题的解决更为完善.

4 通过迁移训练促进知识结构的完善

物理问题的分析和处理需要学生熟练使用各种知识和方法.这些能力都可以在日常的迁移训练中得到发展.教师在教学过程中善于加以引导，并给予方法上的点拨和启发，助力他们相关能力的发展.

例4.如图4所示，直角三角形导线框abc固定在匀强磁场中，ab是一段长为L、电阻为R的均匀导线，ac和bc的电阻可不计，ac长度为.磁场的磁感应强度为B，方向垂直纸面向里.现有一段长度为，电阻为的均匀导体棒MN架在导线框上，开始时紧靠ac，然后沿ab方向以恒定速度v向b端滑动，滑动中始终与ac平行并与导线框保持良好接触，当MN滑过的距离为时，导线ac中的电流为多大？方向如何？

图4

解析：这是一个典型的电磁感应问题，不仅需要学生将电磁感应的知识迁移过来，也需要用到恒定电流的基本知识，为此我们可以提出问题引导学生进行等效处理：图示结构中哪一部分等效于电源，能确定“电源”的正负极吗？能否画出等效电路图？请结合闭合电路欧姆定律解决问题.

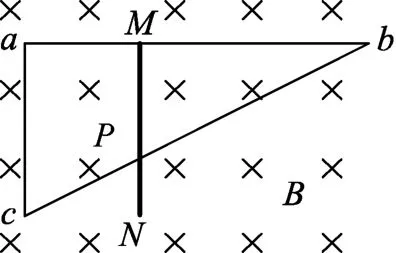
图5

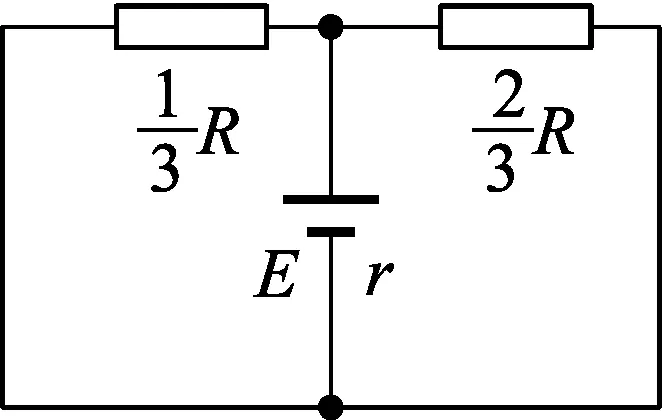
图6

总之，迁移思维是等效法的重要支撑，以等效法的教学引导为切入点，恰当引导可以促进学生迁移思维的发展，且能有效地提升学生的思维品质.