对刚体滚动过程中摩擦力做功问题的探讨

郑 金

（辽宁省凌源市职教中心，辽宁 朝阳 122500）

1 引出问题

原题.如图1所示，半径为R的圆柱体在重力作用下沿斜面连滚带滑地从顶端运动到底端，设斜面的长为L，斜面对圆柱体的滑动摩擦力为f，试研究下滑过程中滑动摩擦力对圆柱体所做的功.

图1

原解：将摩擦力f平移到圆柱体的中心，同时附加力偶矩M＝f R的作用.平移到圆柱体中心的力f在运动过程中做的功等于－f L.设在运动过程中圆柱体转过的角度为φ（由于有滑动，则φR＜L），可知附加力偶矩做的功为Mφ＝f Rφ.所以，摩擦力对圆柱体做的功为W＝－f L＋f Rφ＜0.

探讨：原题及原解来自文献［1］.对于原题，是一道关于刚体在滚动过程中摩擦力做功的问题，但在以往的高中物理竞赛中，有关刚体滚动的试题很少涉及摩擦力做功的计算，由此看来，原题的难度是比较大的.此外，对于原解，虽然算出的功为W＝－f L＋f Rφ，但不是最终结果，因为角度φ是未知量，还需求出角度φ代入.

2 解决问题

在原题中提到“连滚带滑”，这种运动形式属于非纯滚动，只有对非纯滚动才能谈论“滑动摩擦力做功”.鉴于此，首先探究圆柱体发生非纯滚动的条件，然后对摩擦力做的功给出3种求解方法.

2.1 推导圆柱体在斜面上做非纯滚动的条件

设斜面的倾斜角为θ，发生纯滚动的圆柱体侧面受到静摩擦力大小为f′，质心加速度大小为a，由质心运动定理有mg sinθ－f′＝ma.

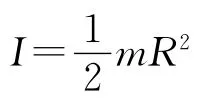
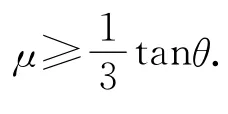
2.2 推导相对滑动路程的关系式及其含义

滑动摩擦力对圆柱体做功，包括两方面，即滑动摩擦力f阻碍圆柱体前进，做负功；同时，滑动摩擦力相对于质心提供一个转动力矩，使圆柱体加速转动，做正功.设质心平动路程为s，侧面转动路程为s1，相对滑动路程为s2，则摩擦阻力对圆柱体做的功为W0＝－fs，摩擦动力对圆柱体做的功为W1＝fs1，可知摩擦力对圆柱体做的总功为

W＝W0＋W1＝－f（s－s1）.

滑动摩擦力属于非保守力，由功能关系可知，滑动摩擦力做功的过程，是机械能减少的过程，即内能增加的过程，因此滑动摩擦力做功的绝对值等于摩擦生热即内能W＝Q＝fs2.

联立方程可知相对滑动路程为s2＝s－s1.这表明，在圆柱体质心平动速度与侧面切向速度方向相反的情况下，相对滑动路程等于质心平动路程与侧面转动路程之差.其中平动路程是假设圆柱体不转动只平动时侧面滑动的路程，即质心运动的路程；转动路程是假设圆柱体不平动只转动时侧面滑动的路程，即侧面相对于质心转动的路程.

值得注意的是，圆柱体克服摩擦力做的功并不等于产生的热量，只有总功的绝对值才等于热量.这如同光滑水平面上的平板车与车上的物块发生相对滑动的过程中摩擦力做的总功，即相互作用的一对摩擦力对系统做的功为负值，其绝对值等于热量，等于摩擦力大小与相对滑动路程之积.

2.3 计算滑动摩擦力做的功

下面给出不同于原解的3种方法.

解法1：间接计算相对滑动路程.

当圆柱体发生滑动时，质心的加速度大小为

a＝g sinθ－μg cosθ.

由运动学公式可得运动时间为

其中动摩擦因数满足f＝μmg cosθ，可知

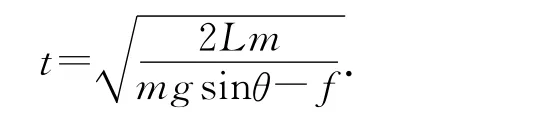
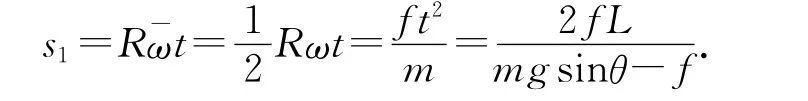
因此相对滑动路程为

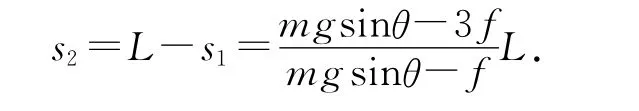
滑动摩擦力做功为

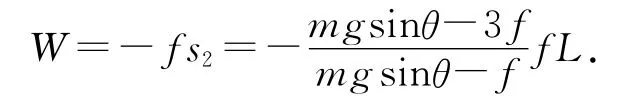
解法2：直接计算相对滑动路程.

由转动定理可知圆柱体转动的角加速度为

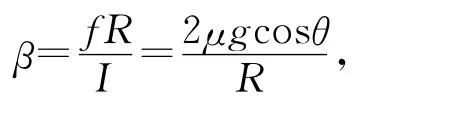
则侧面相对于质心转动的切向加速度为

a1＝βR＝2μg cosθ.

在接触面处，切向加速度方向沿斜面向上，质心加速度方向沿斜面向下，根据相对滑动加速度等于质心平动加速度与侧面切向加速度的矢量和，得

a2＝a－a1＝g sinθ－3μg cosθ.由于初速度为0，则相对滑动的路程为

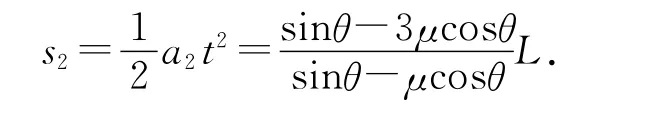
利用f＝μg cosθ可知摩擦力做的总功为

解法3：应用能量守恒定律计算热量.

圆柱体的动能包括质心平动动能与绕质心的转动动能.由能量守恒定律可知摩擦产生的热量为

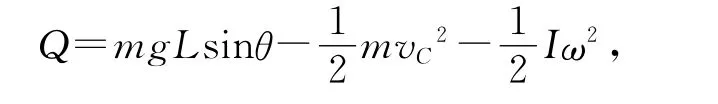
其中vC＝at，ω＝βt.由功能关系知滑动摩擦力做功W＝－Q.

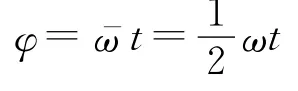
3 结语

综上可见，圆柱体在斜面上滚动过程中的相对滑动路程是一个很抽象的物理量，不仅与轴线平动的路程有关，还与侧面相对于轴线转动的路程有关.若圆柱体侧面相对于质心转动的路程与质心平动的路程不相等，则相对滑动路程不为0，发生非纯滚动.若在接触点处的切向运动方向与质心平动方向相反，则相对滑动路程等于刚体质心平动路程与侧面转动路程之差的绝对值；若在接触点处的切向运动方向与平动方向相同，则相对滑动路程等于刚体质心平动路程与侧面转动路程之和.为了计算相对滑动路程，关键是把刚体的运动分解为质心的平动与侧面绕质心的转动，两个分运动都是匀变速运动，利用运动学公式即可求出各自的路程.但要注意侧面的“匀变速”运动是曲线运动，而且两个分运动的加速度不同.滑动摩擦力做的功为负值，包括两方面，即滑动摩擦力阻碍圆柱体的平动做负功以及使圆柱体加速转动做正功，总功即二者的代数和为负值，其绝对值为圆柱体的机械能变化量，在数值上等于系统产生的热量，等于摩擦力大小与相对滑动路程之积.