钢箱-混凝土组合梁桥竖向温度梯度分析

2023-01-16朱劲松李雨默顾玉辉常文洁

公路工程 2022年6期

朱劲松，李雨默，顾玉辉，常文洁

(1.天津大学建筑工程学院，天津 300072； 2.河北雄安荣乌高速公路有限公司，河北保定 071700； 3.河北省交通建设监理咨询有限公司，河北石家庄 050000)

0 引言

钢-混凝土组合梁能够充分发挥钢和混凝土两种材料的优势，具有自重轻、承载力高、动力性能好、经济性突出和利于工业化建造等优点，已经成为中小跨径桥梁当中极具竞争力的桥型，在我国的桥梁建设中占有重要地位。桥梁结构除了承受静、动力荷载外，还时刻受到自然环境中太阳辐射和气温变化的作用，极端情况下产生的温度效应甚至能超过恒载和活载[1-4]。随着组合梁的普及，国内许多学者对组合梁温度场进行了研究。文献[5]～文献[7]依靠桥梁温度实测数据，研究组合梁桥竖向温度变化规律，指出现有规范规定的组合梁桥竖向温度梯度不能满足实际工程的需要；文献[8]、文献[9]依托有限元软件提出了组合梁桥温度场模拟方法，对组合梁桥温度分布与其影响因素进行了初步研究，指出影响桥梁温度分布的因素主要有环境参数、材料参数、截面参数等。但现阶段对钢箱-混凝土组合梁温度场的研究仍不完善，现有研究大多忽略桥梁结构的多种遮挡作用，缺少对钢箱-混凝土组合梁桥精细温度场研究，现有研究大多针对组合梁桥整体温度变化，对可用于实际工程的竖向温度梯度模式与其影响因素研究较少[5-9]。

本文以河北省某在建高速公路简支钢箱-混凝土组合梁桥为例，建立钢箱-混凝土组合梁桥精细温度场分析模型，通过四季典型天气条件下组合梁桥温度场的分析，研究钢箱-混凝土组合梁桥的竖向温度分布规律与组合梁桥竖向温度分布影响因素。

1 日照温度场分析理论

1.1 日照温度场计算理论

桥梁在自然条件下温度场主要由桥梁结构内部热传导、结构表面所受各种辐射，以及结构与外界环境交流换热决定[10]。

热传导的理论基础为Fourier导热定理，直角坐标系下三维导热微分方程的一般形式为[11]：

(1)

式中：T为结构温度；λ为结构热传导率；ρ为结构密度；c为结构比热容。

桥梁结构在日照作用下的所受自然辐射按辐射类型一般可分为短波辐射与长波辐射[12]。短波辐射一般分为太阳直接辐射Id、散射辐射Is和地表反射辐射Ir。太阳直接辐射Id来自穿过大气层直接到达桥梁表面的太阳光，其取值为[12]：

Id=I0Pm

(2)

式中：I0为太阳常数；P为大气透明度系数，取值可参考文献[13]；m为大气光学质量，可近似取m=cscβs，其中βs为太阳高度角。

散射辐射Is来自经过大气中雾、灰尘等粒子散射的太阳光，其取值为[12]：

Is=0.5I0(1-Pm)/(1-1.4 lnP)sinβs

(3)

反射辐射Ir来自经过地面反射到结构表面的太阳光，其取值为[12]：

(4)

式中：Re为地面反射系数，一般地面取0.2。

与短波辐射来自太阳光不同，长波辐射的辐射源为大地、大气，以及结构表面。长波辐射一般分为大气逆辐射Ia、地表长波辐射Ig、结构表面辐射Im[13]。

大气逆辐射Ia为大气与结构表面交换热量的辐射荷载，其取值为[14]：

(5)

式中：εsa为大气辐射系数，一般取0.8；c0为黑体辐射常数，c0=5.67W/(m2K4)；Ta为环境温度，℃。

地表长波辐射Ig包括地表反射的大气逆辐射，以及地表发射的长波辐射，其取值为[14]：

Ig=c0(Ta+273.15)4

(6)

结构表面辐射Im为结构表面以电磁波形式向外发出的长波辐射，其取值为[14]：

Im=εsc0(Ts+273.15)4

(7)

式中：εs为结构材料的长波辐射发射率；Ts为结构表面温度，℃。

桥梁结构与外界空气的对流换热系数的理论基础为热力学的冷却定律，对流换热在桥梁结构表面形成的热流密度大小qa为[15]：

qa=hc(Ta-Ts)

(8)

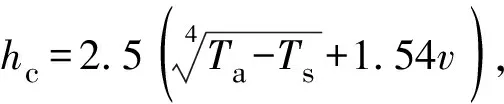
1.2 三维遮挡理论

桥梁的不均匀温度场不仅由热传导、自然辐射、对流换热产生，也由桥梁结构自身或构件间相互遮挡产生，作者将太阳辐射三维遮挡分为如下3种[15]：①永久遮挡，如果桥梁结构某表面释放的热辐射被其他结构吸收，不接受任何形式的热荷载则称该面处于永久遮挡状态，在此类表面不施加任何辐射荷载，如图1(a)所示；②自遮挡，如果桥梁结构某表面在某时间段内太阳入射角大于90°，则称该表面处于自遮挡状态，处于自遮挡状态的桥梁表面所接受的太阳辐射强度为0，如图1(b)所示；③相互遮挡，在某时段桥梁结构某面上的部分点由于桥梁其他构件的遮挡作用而无法受到阳光直射，则称该时段此部分点处于互遮挡状态，处于互遮挡状态的构件面接受的太阳辐射强度为0，如图1(c)所示。

图1 三维遮挡类型

1.3 日照温度场数值分析实现方法

依托日照温度场理论对DFLUX与DFLIM进行二次开发：在DFLUX子程序中，对结构表面进行分类，将处于永久遮挡的内表面点坐标储存于集合中，在温度分析前进行永久遮挡判断，将永久遮挡的辐射荷载设置为0，实现永久遮挡；定义构件表面法线与太阳光线之间的夹角为太阳入射角，将太阳入射角为钝角时刻的太阳辐射设置为0，实现自遮挡；确定桥梁表面所受太阳光线方程的方向向量和潜在的对该表面存在相互遮挡的表面，根据光线追踪检测原理[15]，对太阳光线与潜在的遮挡表面进行相交判断，如果相交则说明两表面存在相互遮挡，将被遮挡的表面所受太阳直接辐射设置为0，实现互遮挡；在DFILM子程序中通过定义与风速、环境温度相关的对流换热系数函数实现非均匀对流换热系数的定义与施加。

1.4 分析方法验证

采用参考文献[16]中2013年9月25日进行的钢箱-混凝土组合梁桥室外日照试验结果对本文提出的桥梁结构三维温度场数值模拟方法进行验证。

试验所在地纬度E116.34°，N39.95°，试验梁为东西走向，试验当日气温变化范围15 ℃～36 ℃，当日地表平均风速2.0 m/s，混凝土表面太阳辐射吸收系数0.65，辐射发射系数0.91，钢材表面太阳辐射吸收系数0.685，辐射发射系数0.8。选择4个温度测点对有限元模拟温度方法进行对比验证，测点布置与对比结果如图2所示。

由图2可知，模拟计算所得组合梁温度与实测温度变化趋势大体一致，模拟实测差值最大为1.8 ℃。综上所述，模拟计算方法能较准确地模拟出实际钢箱-混凝土组合梁的温度变化规律，满足研究的需要。

(a)测点布置

2 有限元模型分析

2.1 有限元模型建立

以河北省某在建的跨度72 m的钢箱-混凝土组合梁桥为例，桥面宽度为20.5 m，钢箱梁底宽2.8 m，横断面形式为单箱单室，箱室之间采用横梁连接，钢梁高度2.6 m，桥面板厚度0.4 m，桥面铺装为0.1 m的沥青混凝土，翼缘板悬臂长度1.2 m，横断面示意图如图3所示。工程的地理坐标为E116.10°，N 39.16°，工程桥址方位角北偏东73.5°。

图3 钢箱-混凝土组合梁桥横断面示意图(单位：mm)

采用通用有限元软件ABAQUS建立实例钢箱-混凝土组合梁桥精细有限元模型，混凝土板与沥青层采用传热实体单元DC3D8，钢箱梁采用传热壳单元DS4，单元数量105 976。建立三维组合梁桥模型如图4所示。组合梁桥各构件材料热物性参数如表1所示[11，17]。

图4 钢箱-混凝土组合梁桥温度场计算模型

表1 材料热物性参数Table 1 Materials thermo-physical parameter材料密度/(kg·m-3)比热容/[J·(kg·K)-1]热传导率/[W·(m·K)-1]辐射吸收系数辐射发射系数钢7 85046050 0.6850.8混凝土2 600925 2.00.650.88沥青2 3801 050 1.60.90.92

2.2 分析工况

根据中国气象数据网中工程所在地区2014—2019年的气象资料，确定工程所在地四季典型气象参数取值如表2所示。

2.3 钢箱-混凝土组合梁桥竖向温度梯度

为了研究钢箱-混凝土组合梁竖向温度梯度变化规律，确定竖向温度提取路径，即取竖向温度梯度最显著的南北两端钢腹板中线所在位置作为竖向温度提取位置，如图3所示。

夏季典型天气下组合梁竖向温度分布变化情况如图5所示，其中为了更加清楚地表现出沥青铺装层和混凝土桥面板的竖向温度分布的变化情况，将沥青铺装层与混凝土桥面板的厚度放大两倍。

由图5可知，组合梁的竖向温度分布可以根据桥面板的温度分布分为降温与升温两种模式。由于沥青和混凝土的导热性能较差，混凝土内部温度变化落后于环境温度变化，桥面板处于向外界散发日间储存热量的降温过程，本文将这种桥面板温度中间高两端低的竖向温度分布模式定义为降温模式，如图6(a)所示。随着太阳的升起，太阳辐射和环境温度增加，桥面板温度逐渐升高，上部的温度升高速率高于下部的速率，使得桥面板的上部温度高于下部温度，本文将这种桥面板温度上高下低的竖向温度分布模式定义为升温模式，如图6(b)所示。

(a)降温模式(1∶30)

组合梁的竖向温度分布处在随时间不断变化的过程中，但在实际工程计算中采用的是最不利的温度分布情况，所以需要确定最不利的竖向温度梯度。取梁截面上温度变化最小的一点的温度作为基准温度，根据各点的温度分布形式得出梁截面各点相对于基准温度点的温差分布形式，取温差之和最大时刻的竖向温度分布为最不利的竖向温度梯度，实际工程中不考虑沥青铺装层组合梁共同受力，所以计算最不利的竖向温度梯度时不考虑沥青铺装层的温度。

现行规范中常采用负值表示负温度梯度，所以采用负值表示降温模式的竖向温度梯度。本文选择混凝土桥面板底面温度作为基准温度，取得四季典型天气条件下的最不利竖向温度梯度，如图7所示。

(a)升温模式(14∶00)

由图7可知，不同季节的两种模式的最不利竖向温度梯度形状基本一致，夏季竖向温度梯度相较其他季节更为不利，其中最不利的升温模式出现于下午14∶00，最不利的降温模式出现于凌晨1∶30。

2.4 竖向温度梯度的简化

为了更好地适应实际工程计算需要，对竖向温度梯度进行简化，采用上部双折线与下部等温段简化两种模式的竖向温度梯度，简化后的竖向温度梯度可由4个温差基数和3个位置基数表示，见图8。

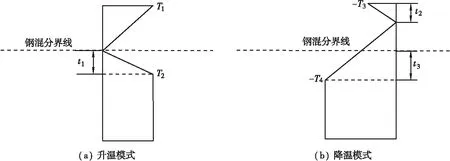
图8 简化竖向温度梯度模式

3 竖向温度梯度影响因素研究

为了研究各种因素对组合梁温度分布的影响，总结各种温度分布影响因素并将组合梁温度分布影响参数分为3类：环境参数、材料参数、结构参数。通过改变不同参数设置的方法进行参数分析，研究各种参数变化对组合梁竖向温度梯度的影响规律。

3.1 环境参数

3.1.1桥梁方位角

桥梁选址过程中，桥梁方位角也在不断变化，使得桥梁构件受到的太阳自然辐射不同，导致温度分布不同。为了研究桥梁走向对竖向温度梯度的影响，依托前文夏季典型天气温度场计算，桥梁走向设置如表3所示。

表3 桥梁走向设置Table 3 Bridge azimuth settings编号桥梁走向1南北走向2东西走向3 南偏东45°4北偏东45°

由温度场计算结果可知，桥梁走向变化仅对升温模式的温差基数T2有较大影响，不同桥梁走向的T2取值如图9所示。

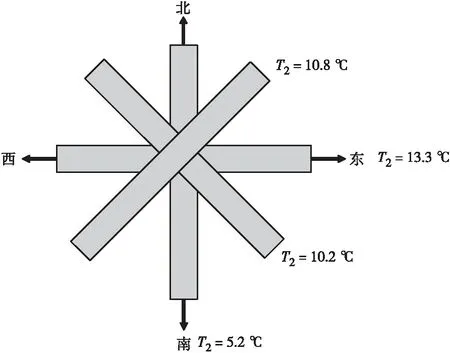
图9 不同桥梁走向的温差基数取值

由图9可知，T2在东西走向时取得最大值13.3 ℃，在南北走向时取得最小值5.2 ℃，其变化幅度为8.1 ℃，而南偏东与北偏东走向的温差基数T2较为相似，都在10 ℃左右，应根据实际的桥梁走向，按照式(10)确定温差基数T2。

3.1.2纬度

我国幅员辽阔，纬度变化范围较大，纬度的变化通过改变太阳倾角使得桥梁构件所受的太阳辐射不同。依托前文夏季典型天气温度场计算，研究纬度对组合梁竖向温度分布模式的影响规律，我国大陆纬度变化范围为北纬18°(三亚市)和53°(黑龙江漠河县)，由此可如表4设置纬度。

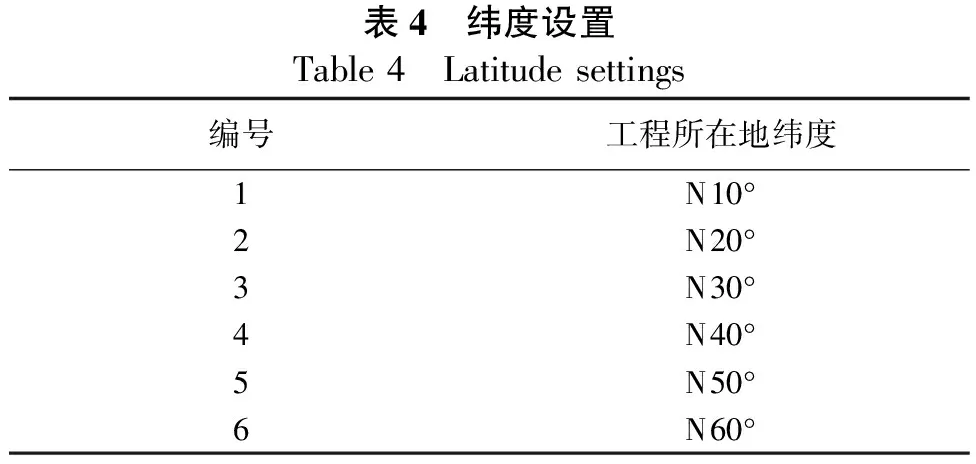
表4 纬度设置Table 4 Latitude settings编号工程所在地纬度1N10°2N20°3N30°4N40°5N50°6N60°

由不同纬度的温度场计算结果可知，纬度变化仅对温差基数有影响，不同纬度下温差基数取值如图10所示。

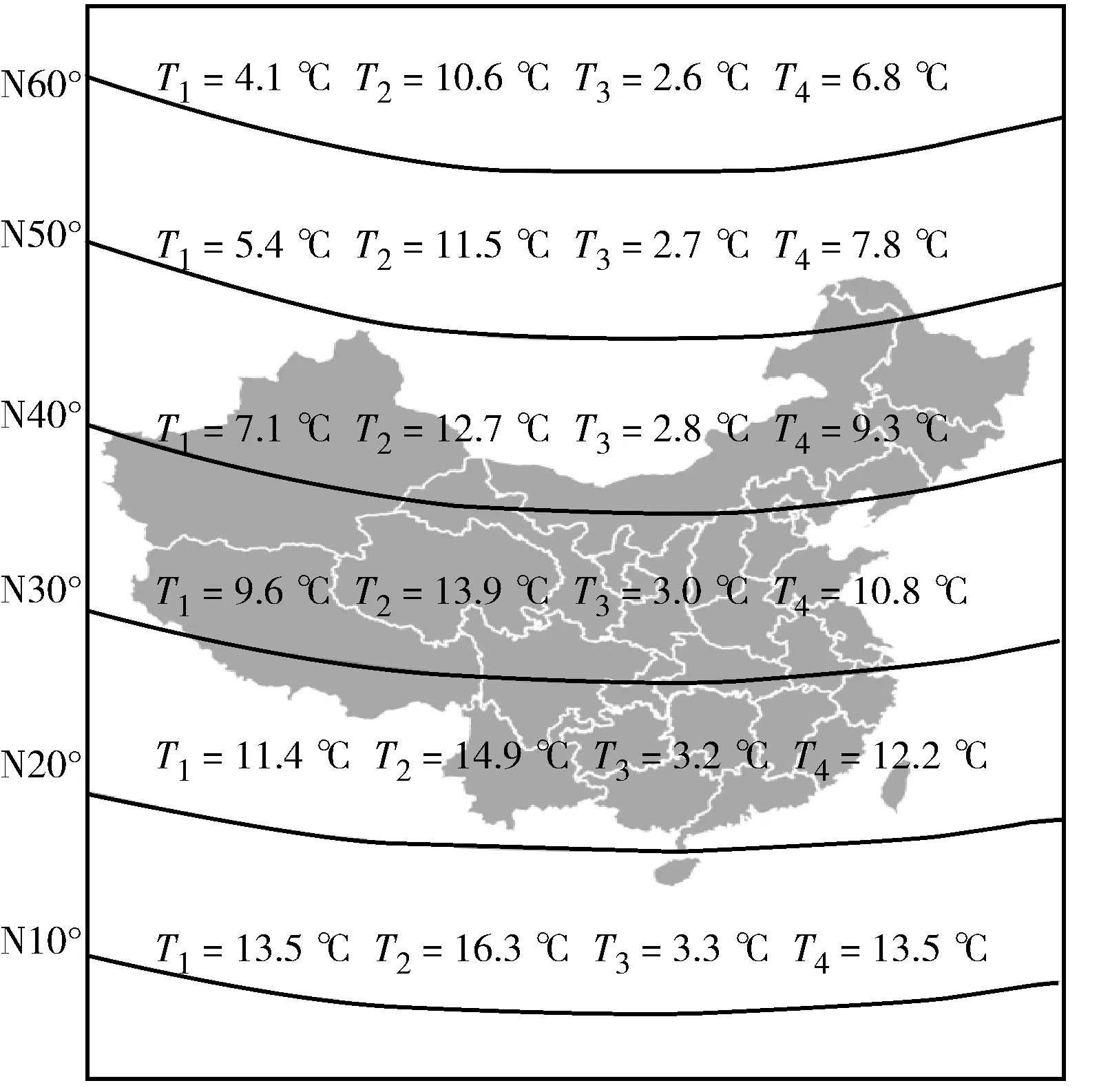
图10 不同纬度的温差基数取值

由图10可知，温差基数与纬度之间存在线性关系，随着纬度的增加，两种温度分布模式的温差基数T1、T2、T3、T4均减小，但纬度变化对T3的影响较小，可忽略不计，不同纬度地区的T1、T2、T3的取值可根据图10结果插值得到。

3.1.3风速

风速主要影响桥梁结构的对流换热系数，从而影响温度场分布。风速在内陆城市一般较小，在东南沿海与西北相对较大。具体而言，新疆喀什地区地表日均风速可达六级强风(10 m/s)，内陆有的城市地表日均风速则只有l级微风(1 m/s)。依托前文夏季典型天气温度场计算，地表日均风速设置取值如表5所示。

表5 地表日均风速设置Table 5 Daily average surface wind speed settings编号地表日均风速/(m·s-1)11.024.037.0410.0

由不同风速的温度场计算结果可知，风速变化仅对温差基数T1、T2、T4有较大的影响，不同风速下的温差基数取值如图11所示，由图11可知，温差基数T2变化的幅度最大，为3.5 ℃，这是由于随着风速的增大，钢梁的对流换热系数增大，使得钢梁积累的太阳直接辐射减少，钢梁的温度逐渐降低接近环境温度，T1、T4的变化范围分别为3.0 ℃、1.7 ℃。温差基数T1、T2、T4的取值可根据工程所在地地表风速取值，在图11结果中采用线性插值的方法取得。

图11 不同地表日均风速的温差基数取值

3.1.4环境温度

环境温度通过影响桥梁结构所受长波辐射和结构表面对流换热来影响组合梁温度分布，影响一天温度的主要参数为环境最高温度。依托前文夏季典型天气温度场计算，我国夏季最高温度一般在35 ℃～40 ℃之间，由此可设置组合梁温度场计算所用最高温度，如表6所示。

表6 环境最高温度设置Table 6 Maximum ambient temperature settings编号环境最高温度/℃135236337438539640

由不同环境最高温度的下温度场计算结果可知，环境最高温度仅对温差基数有影响。随着环境最高温度的升高，温差基数均增大。由于沥青与混凝土热传导率较低，混凝土温度对外界温度变化并不敏感，因此顶部温差基数T1、T3变化范围很小，可忽略不计。而下部钢梁温差基数则受温度变化影响较大，T2、T4随环境最高温度的升高分别增大3.1 ℃、2.0 ℃，不同环境最高温度下钢梁温差基数T2、T4取值如图12所示。

图12 不同最高温度的温差基数取值

由图12可知，钢梁温差基数与环境最高温度近似为线性关系，在确定实际工程所用的竖向温度梯度时，应考虑环境最高温度的影响，根据图12的结果插值计算得到钢梁温差基数T2、T4。

3.2 材料参数

钢材的热物性参数较为稳定，混凝土和沥青则因为原料问题，热物性参数在一定范围内变化[10]。混凝土和沥青材料的比热容变化幅度较小，一般仅考虑辐射吸收系数和热传导率的影响。桥梁表面受到太阳辐射的大部分为沥青材料，所以一般只考虑沥青的辐射吸收系数的影响，并且由于沥青铺装层厚度一般较小，所以仅考虑混凝土热传导率对温度分布模式的影响。依托前文夏季典型天气温度场计算，通过改变材料热物性参数设置的方法进行参数分析，研究沥青的辐射吸收系数和混凝土的热传导率对组合梁温度分布模式的影响规律。

3.2.1沥青辐射吸收系数

沥青辐射吸收系数影响沥青铺装层表面吸收太阳辐射的大小，进而影响温度分布。沥青辐射吸收系数的变化范围在0.6～0.9之间，沥青辐射吸收系数设置如表7所示。

表7 沥青辐射吸收系数设置Table 7 Solar radiation absorbing coefficient of asphalt settings编号沥青辐射吸收系数10.620.730.840.9

由温度场计算结果可知，沥青辐射系数仅对温差基数有影响。由于夜间太阳辐射的消失，沥青辐射吸收系数的变化对降温模式的温差系数T3、T4的影响并不大，变化幅度仅为0.2 ℃、0.4 ℃，变化可忽略不计，而沥青辐射吸收系数变化对T1、T2有较大，变化幅度分别为2.4 ℃、2.1 ℃，不同沥青辐射吸收系数的升温模式的温差基数取值如图13所示。

图13 不同沥青辐射吸收系数的温差基数的取值

由图13可知，沥青辐射吸收系数与升温模式温差基数存在线性关系，对于实际工程中采用较低辐射吸收系数的沥青铺装层的组合梁，可根据图13的结果插值取得升温模式温差参数。

3.2.2热传导率

混凝土的热传导率变化范围一般为1.5～3.0 W·(m·K)-1[17]，混凝土热传导率设置如表8所示。

表8 混凝土热传导率设置Table 8 Thermal conductivity of concrete settings编号混凝土热传导系数/[W·(m·K)-1]11.522.032.543.0

由温度场计算结果可知，混凝土热传导率的变化仅对温差基数有影响，对T4的影响很小，其变化幅度仅为0.4 ℃，可以忽略不计，而热传导率对其余温差基数有较大影响，T1、T2、T3的变化幅度分别为2.9 ℃、3.9 ℃、1.3 ℃，不同热传导率的温差基数取值如图14所示。

图14 不同混凝土热传导率温差基数

随着混凝土热传导率的增大，混凝土桥面板内部温度差异变小，即混凝土桥面板温度沿深度的变化率逐渐变小，因此两种模式下的上部温差基数T1、T3随热传导率的升高而线性降低，由于热传导率的升高，白天有更多的热量传递到混凝土下部，混凝土下部温度升高，因此下部温差基数T2线性降低。在确定实际工程所用的竖向温度梯度时，应考虑混凝土传导率的影响，温差基数T1、T2、T3的取值可根据混凝土热传导率取值，在图14结果中线性插值取得。

3.3 截面参数

3.3.1铺装层厚度

混凝土桥面板铺装层厚度一般为0～0.1 m，由于沥青的辐射吸收系数比混凝土大，导致桥面板上部接受的热量较多，从而影响组合梁温度场的分布，铺装层厚度工况设置如表9所示。

表9 铺装层厚度设置Table 9 Pavement thickness settings编号铺装层厚度/m10 20.0530.10

不同铺装层厚度下组合梁桥最不利的竖向温度梯度模式如图15所示。

(a)升温模式

由图15可知，由于沥青铺装层对混凝土桥面板有较强的隔热作用，随着沥青铺装层厚度的增大，上部温差基数呈线性减小的趋势，T1、T3变化幅度分别为5.1 ℃、3.4 ℃。降温模式的位置参数t2也与铺装层厚度有关，对于无铺装组合梁桥，t2取值增大至0.25 m。而沥青铺装层的变化对下部钢梁温差基数T2、T4影响变化幅度分别为0.2 ℃、0.6 ℃，其变化可以忽略不计。由此，应根据实际工程的铺装层确定竖向温度梯度的上部温差基数T1、T3与降温模式的位置参数t2。

3.3.2翼缘悬臂长度

桥面板翼缘悬臂长度影响钢腹板太阳直射的区域，从而影响组合梁的温度分布。翼缘悬臂长度的取值范围为0.5～2.0 m，依托前文夏季典型天气温度场计算，翼缘悬臂长度设置如表10所示。

表10 翼缘悬臂长度设置Table 10 Flange cantilever length settings编号翼缘悬臂长度/m10.521.031.542.0

由温度场计算结果可知，翼缘悬臂长度的变化仅对升温模式的温差基数T2和位置基数t1有较大影响，随着翼缘悬臂长度的增长，T2呈线性减小趋势，t1呈线性增大的趋势，其变化幅度分别为3.3 ℃、1.0 m，而翼缘长度变化对其它基数影响可忽略不计，不同翼缘长度的竖向温度梯度基数取值如图16所示。因此对较大翼缘悬臂长度的实际工程，应对升温模式的温差基数T2和位置参数t1进行调整。

图16 不同翼缘长度的温度梯度基数取值

3.4 钢箱-混凝土组合梁桥竖向温度梯度基数回归函数

由上述温度场计算结果分析可知，钢箱-混凝土组合梁桥竖向温度梯度基数与影响参数之间存在线性关系，为了量化研究结果，更好地指导实际工程，应用多元线性回归的方法，确定竖向温度梯度的温度基数与前文参数分析确定的影响较大的因素之间的函数关系。

A～H依次对应前文桥梁方位角、纬度、风速等影响因素，温差基数的影响因素回归函数如式(9)～式(12)所示，位置基数的影响因素回归函数如式(13)～式(15)所示：

T1=12.87-0.2B-0.45C+12.66E-

2.67F-0.04G，(R2=0.90)

(9)

T2=12.36-0.09A-0.11B-0.43C+

0.53D-5.38E-2.12F-2.58H，

(R2=0.94)

(10)

T3=7.52-0.77F-0.03G，(R2=0.99)

(11)

T4=8.39-0.14B-0.32C+0.18D，

(R2=0.94)

(12)

t1=0.66H，(R2=0.96)

(13)

t2=0.25-F，(R2=0.99)

(14)

t3=1，(R2=1)

(15)

式中：T1、T2、T3、T4为温差基数，℃；t1、t2、t3为位置基数，m；A为桥梁方位角，(°)，取值范围0°～90°，其中东西走向为0°，南北走向90°；B为纬度，(°)，取值范围为10°～50°；C为工程所在地地表日平均风速，m/s，取值范围1～10 m/s；D为工程所在地最高环境温度，取值范围为35 ℃～40 ℃；E为沥青辐射吸收系数，取值范围为0.6～0.9；F为混凝土热传导率，取值范围为1.5～3.0W/(m·K)；G为沥青铺装层厚度，取值范围为0～0.1 m；H为翼缘长度，取值范围为0.5～2.0 m。