顾及似大地水准面趋势变化的高程异常拟合方法

赵保成 李国忠 徐 坚 徐 健 肖 潇

(1. 长江科学院 空间信息技术应用研究所, 湖北 武汉 430010; 2. 武汉市智慧流域工程技术研究中心, 湖北 武汉 430010)

0 引言

2020年北斗3号全球组网成功,国际上基本形成了以美国全球定位系统(global positioning system,GPS)、俄罗斯格洛纳斯、欧盟伽利略、中国北斗为主的四大全球卫星导航定位系统。伴随着各星座系统导航卫星数目的增加以及迭代更新,全球导航定位系统(global navigation satellite system,GNSS)在各行各业的应用也将越来越广泛,尤其对于测绘地理信息行业。GNSS测量具备全天时、全天候、累积误差小、测站不受通视条件影响的优点,它的出现极大提升了测绘作业效率[1-3]。但是GNSS接收机直接获取的测点高程信息是基于参考椭球面的大地高,而在实际工程应用中,我国使用的却是基于似大地水准面的正常高,在不考虑垂线偏差影响的情况下,二者之间存在一个非固定差值即高程异常,因此,如何求取测点高程异常值成为GNSS高程数据成果直接应用于实际工程中需首要解决的关键问题。

针对上述关键问题,众多行业学者做出了诸多的尝试。文献[4]利用基于稳健估计的总体最小二乘算法较好地解决了高程异常曲面拟合过程中已知点平面坐标与高程异常值中均含有误差的问题;文献[5]提出了一种基于多面函数和移动曲面法的综合高程异常拟合模型,在一定程度上提高了高程异常拟合精度;文献[6]将多种常见高程异常曲面拟合模型进行加权组合,对不同地形的适应性进行了分析;文献[7]利用全球超高阶地球重力场模型(Earth gravitationational model 2008,EGM2008)去除高程异常中的长波项,进而使用加权组合模型对高程异常的剩余项拟合,拟合效率得到了一定的提升;文献[8]提出了蚁群—遗传算法结合多面函数拟合的改进曲面拟合方法,在很大程度上提高了拟合模型的精度;文献[9]基于二次曲面和EGM2008全球重力场模型,构建了多种移去—恢复型函数拟合模型,探究了各种模型的适用性;文献[10]利用矿区水准观测数据及重力场模型,综合物理和几何方法建立了矿区似大地水准面模型;文献[11]构建了二次曲面—径向基函数(radial basis function,RBF)神经网络组合的GPS高程转换模型,提高了单一模型的拟合精度。

综上所述,现有的高程异常拟合研究多是从拟合函数模型角度自身出发,或是模型的改进,或是多种模型的加权组合,缺少了对参与高程异常曲面拟合的特征点的选取方法的研究,特征点若选取不当,将导致拟合曲面关键信息丢失,影响最终的拟合效果。

本文在总结了多位行业学者研究成果的基础上,提出了一种顾及似大地水准面趋势变化的高程异常拟合方法,首先利用SGG-UGM-2全球重力场模型预先获取测区似大地水准面趋势面特征点,后对特征点进行GNSS水准联测,最后结合移去恢复法及二次多项式曲面进行高程异常拟合。经过实例验证,本文提出的高程异常拟合方法,参与高程异常曲面拟合的特征点选取更加合理,关键信息损失少,拟合精度能够达到厘米级,完全满足绝大多数大比例尺地形图测量要求。

1 高程系统

我国常用的高程系统有3种,大地高、正高和正常高。大地高H为测点沿法线至参考椭球面的距离,可由GNSS接收机测得;正高h为测点沿铅垂线至大地水准面的距离,此值为理论值,一般不可直接测得;正常高hr为测点沿铅垂线至似大地水准面的距离,一般通过水准测量方法确定[12]。三者的几何关系如图1所示,数学关系见式(1)与式(2)。我国法定使用的1985国家高程基准使用的高程系统即是正常高系统。式(1)中ζ表示高程异常,式(2)中N表示大地水准面差距。

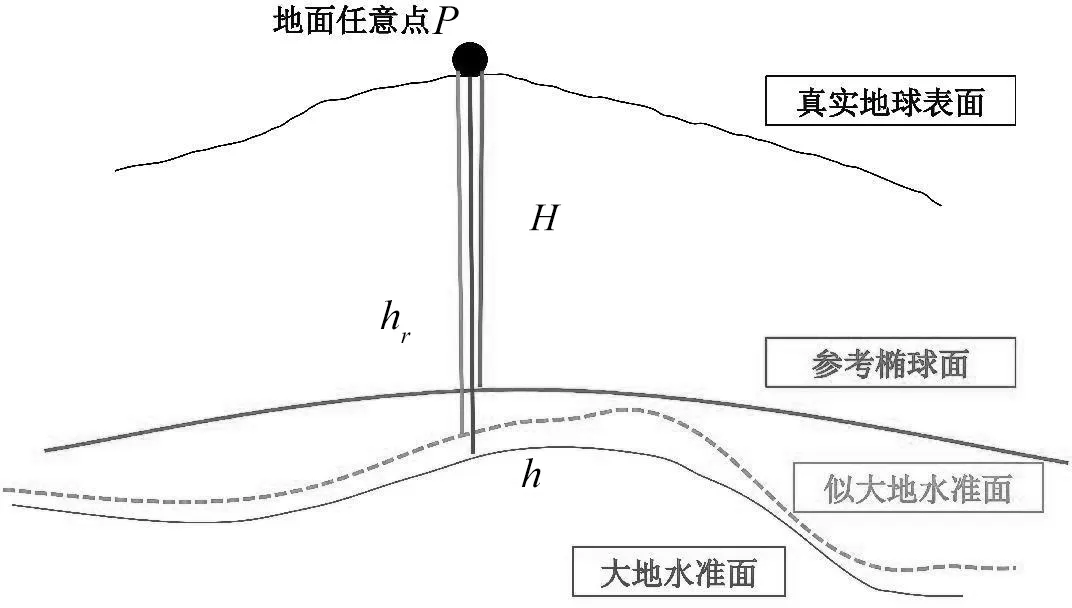
图1 高程系统关系图

2 原理与方法

2.1 利用SGG-UGM-2全球重力场模型求解高程异常中长波项

SGG-UGM-2全球重力场模型是由我国梁伟等学者于2020年采用球谐分析方法构建并发布的一个最新的2 190阶2 159次全球重力场模型,模型分辨率为5′,构建此模型使用的数据包括全球卫星重力观测数据、卫星测高数据和EGM2008全球重力场模型的重力异常数据[13],在我国,此模型精度优于其他全球重力场模型(如SGG-UGM-1、EGM2008等)。以SGG-UGM-2全球重力场模型为基础,利用Bruns公式[14]求解地球上任意点的高程异常中长波项ζGM,公式如下:

(3)

2.2 二次多项式曲面拟合

曲面拟合常用的方法有二次多项式曲面拟合、多面函数法、曲面样条函数法、移动曲面法等。在实际工程应用中,为方便计算,大多采用二次多项式曲面函数拟合高程异常短波项,其数学表达如式(4)所示。

(4)

式中,ζ短波为特征点的高程异常短波项;(xi,yi)为特征点在某参考系统内的平面直角坐标;(a0,a1,a2,a3,a4,a5)为曲面模型待定系数。

根据列立方程组可知,共有6个未知数,因此为求解模型系数,至少需要列立6个方程。当已知点个数大于6时,其表达如式(5)所示。

(5)

将式(5)变换为误差方程形式，如式(6)所示,其中，ε为模型的拟合残差。

(6)

根据最小二乘法原理,令模型拟合残差平方和最小(i≥6),在此条件下,可以求得二次多项式曲面模型待定系数X,见式(7),其中式(8)中的P为权矩阵。

2.3 方法总体流程

根据物理大地测量学理论,任意测点高程异常可由为中长波项与短波项构成,中长波分量变化较小,趋势相对平缓,短波分量主要由地形起伏引起,变化相对较大[15-16],其数学关系如式(9)所示。

(9)

移去恢复法是高程异常拟合的经典方法,该方法能够有效地去除无关变量对拟合最终结果的影响,移去恢复法思想为：首先将高程异常中变化较小的中长波分量移除,然后对短波项进行曲面拟合并通过插值计算出待求点上的短波项,进而在待定点上恢复中长波分量,最终获取待求点上的高程异常。本文提出的顾及似大地水准面趋势变化的高程异常拟合方法对经典的移去恢复法做了相应的改进,其具体操作流程如图2所示。

图2 移去恢复流程图

第一步：确定测区范围并将其格网化,采用SGG-UGM-2全球重力场模型计算测区格网点的高程异常值(真实高程异常中的中长波项),构建基于高程异常中长波项的似大地水准面模型并将其图形化显示。

第二步：利用ArcMap软件中的空间分析模块对上一步得到的似大地水准面曲面模型进行地形表面分析,计算其高程异常极大值、极小值、坡向、坡度、曲率等参数,合理选择似大地水准面趋势变化较大的特征点作为GNSS水准联测点,通过GNSS水准方法求出特征点的真实高程异常值。

第三步：特征点的真实高程异常值减去第一步中计算得到的中长波分量,剩余高程异常短波项。以特征点的平面坐标作为输入值,高程异常短波项作为输出值,构建二次多项式曲面拟合模型,根据模型曲面方程求解特征点覆盖范围内的任意待求点的高程异常短波项。

第四步：利用SGG-UGM-2全球重力场模型计算出待求点的中长波分量,再加上拟合步骤中该点高程异常短波项,最终得到待求点的高程异常值。

3 实验验证

3.1 实验区概况

实验区位于长江中游城市—武汉市,该区域属于江汉平原,相对高差较小。实验区沿武汉市某河流岸线布置,长度约70 km,宽度约0.3 km,实验区具有狭长条形特点。实验区内均匀地设置有若干等精度GNSS水准联测点,点位平面按照《全球定位系统(GPS)测量规范》中D级点要求施测,点位高程按照《国家三、四等水准测量规范》中的三等点要求联测。

3.2 实验区似大地水准面趋势分析

由于实验区呈线状分布,因此选择将实验区内GNSS水准联测点自河流上游至下游串联起来,利用式(1)计算GNSS水准联测点的高程异常值真值,同时利用SGG-UGM-2全球重力场模型计算GNSS水准联测点高程异常中长波分量,两者对比结果如图3所示。 GNSS水准联测点的高程异常值中的中长波分量与高程异常的真值变化趋势基本一致,基本反映了实验区内似大地水准面趋势变化情况;实验区内高程异常值均为负值,说明实验区似大地水准面整体位于椭球面(2000国家大地坐标系椭球)之下,高程异常的最小值为-15.821 m,最大值为-14.254 m,相差1.567 m,沿河流上游至下游,自西向东,高程异常值的绝对值逐渐变小;实验区河流中上游段高程异常值变化近似呈线性规律,下游段高程异常值变化剧烈,整体呈现非线性变化特征。

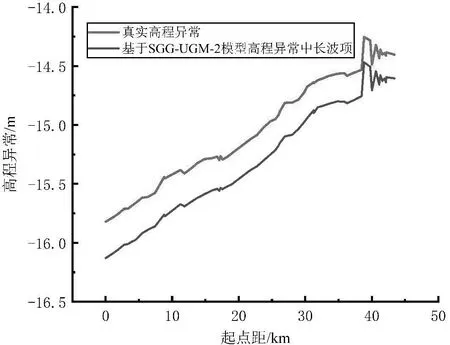
图3 实验区似大地水准面趋势

对于本实验区的高程异常拟合特征点选取工作：①需保证GNSS水准联测点覆盖整个测区；②设置GNSS水准联测点的点数需确保高程异常拟合曲面方程有解;③根据似大地水准面的地形分析结果,GNSS水准联测点需在似大地水准面变化大的区域(实验区下游区)尽量多选点。

3.3 实验方案设计

为验证本文提出的高程异常拟合方法的优越性,采用二次多项式曲面拟合法、移去恢复型二次多项式曲面拟合法、顾及似大地水准面趋势变化的二次多项式曲面拟合法、顾及似大地水准面趋势变化的移去恢复型二次多项式曲面拟合法4种拟合方案进行高程异常拟合效果对比实验,将4种实验方案分别编号为方案1#、方案2#、方案3#、方案4#,如表1所示。

表1 拟合实验方案表

为减少无关变量对实验对比结果的影响,4种方案选择GNSS水准联测点数量均为8个(最少点数为6),检核点均为6个,特征点采用黑色圆形表示,检核点采用三角形表示,各方案的点位选择空间分布如图4所示。

(a)方案1#选点方案

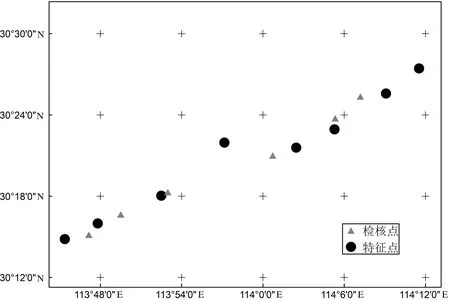
(b)方案2#选点方案

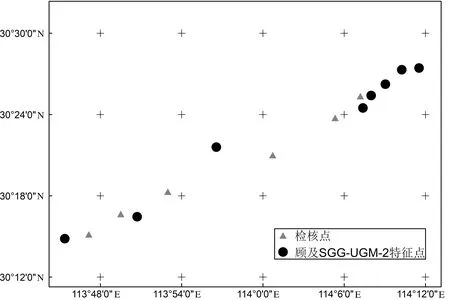
(c)方案3#选点方案

(d)方案4#选点方案图4 各实验选点方案

3.4 精度评定

中误差对一组测量值中的异常值非常敏感,能较好地反映测量结果波动大小,因此本次实验使用中误差评定高程异常拟合精度,计算中误差的表达见式(10)。

(10)

其中,mζ为高程异常拟合中误差;Δ为在检核点上曲面拟合模型插值计算的高程异常值与GNSS水准计算得出的高程异常值(真值)的差值;n为检核点的个数。

3.5 实验对比分析

对比4种方案的拟合效果,由图5和表2的结果可得：

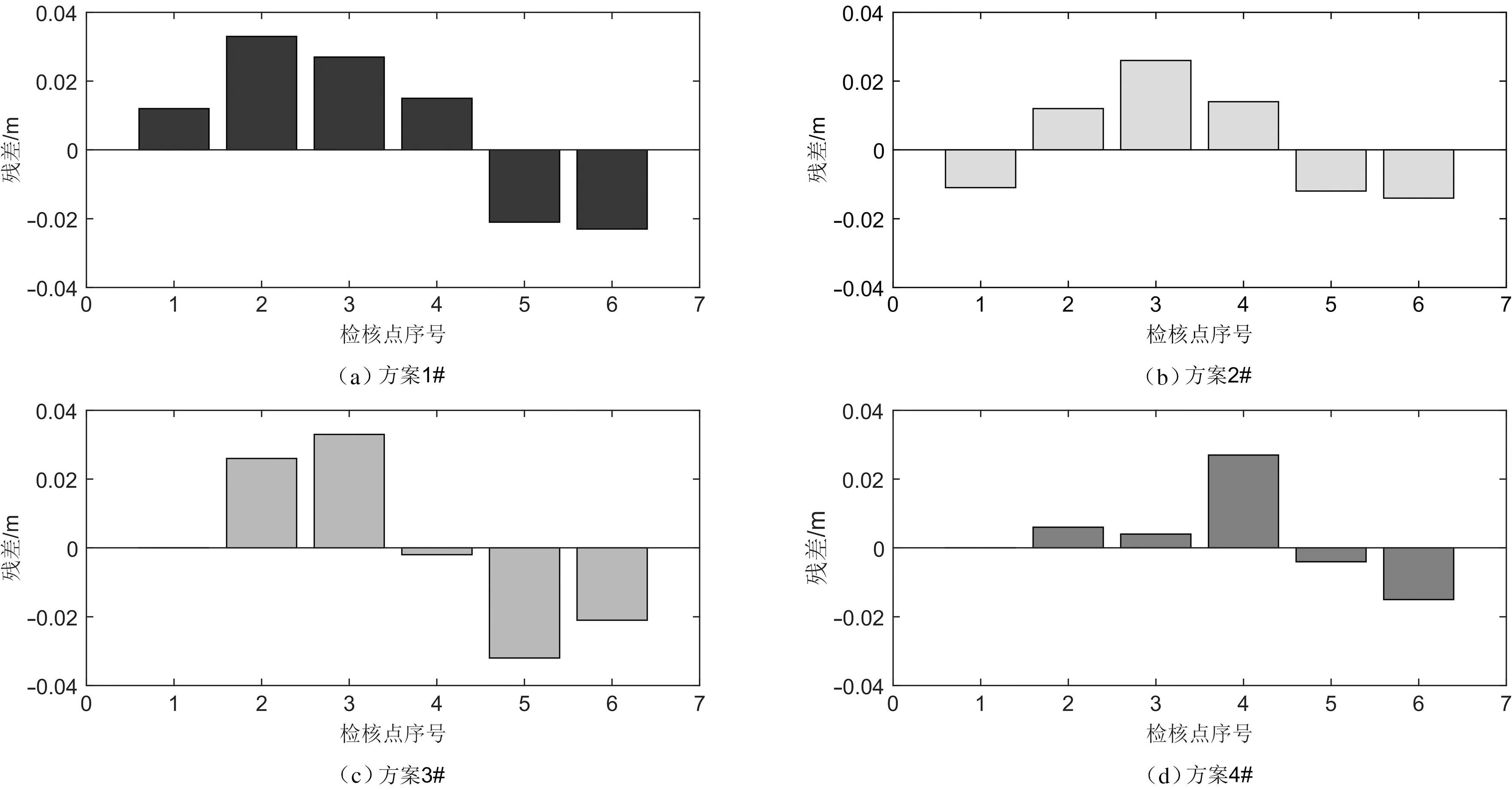
图5 拟合残差图

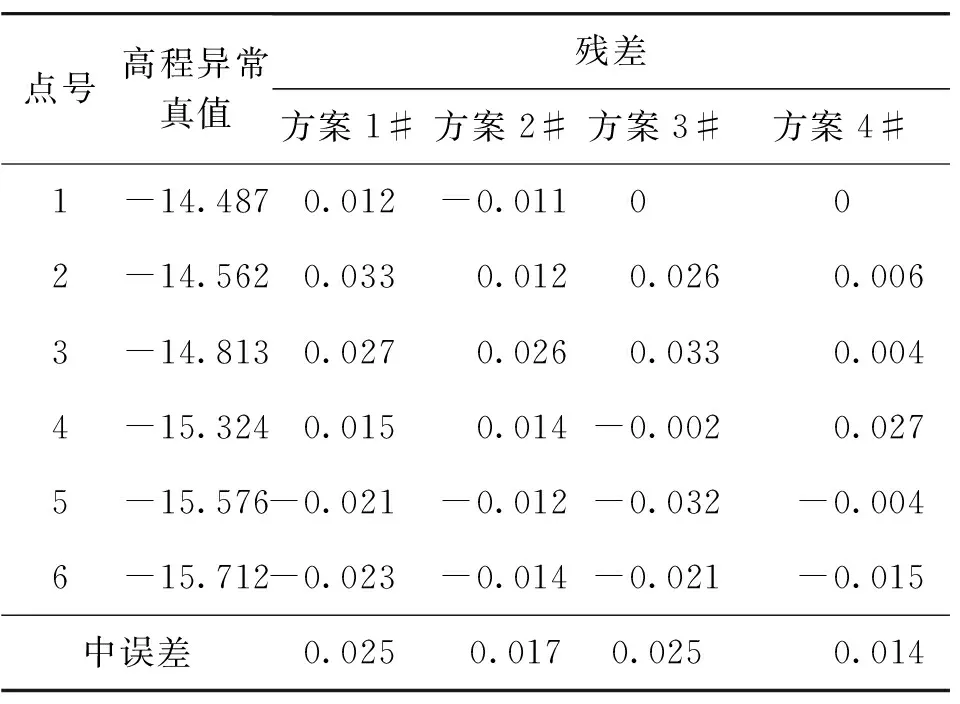
表2 精度评定表 单位：m

(1)不考虑似大地水准面趋势变化选择拟合特征点且不使用移动恢复法的方案1#的高程异常拟合效果最差,最大残差值为0.033 m,最小残差值为0.012 m,中误差为±0.025 m;选择似大地水准面趋势面特征点参与曲面拟合且使用移去恢复法的方案4#拟合效果最好,最大残差值为0.027 m,最小残差值为0.000 m,中误差为±0.014 m。

(2)对比方案1#与方案3#,二者均未采用移去恢复法,拟合中误差均为±0.025 m,总体拟合效果相当;方案3#考虑了似大地水准面趋势变化,相比方案1#的拟合残差的极大值和极小值都小,在未采用移去恢复法的情况下,考虑似大地水准面趋势变化有助于提高高程异常拟合精度,但是总体拟合效果并不明显。

(3)对比方案2#与方案4#,二者均采用了移去恢复法,方案4#考虑了似大地水准面趋势变化,其拟合中误差为±0.014 m,方案2#拟合中误差为±0.017 m,方案4#比方案2#总体拟合精度提升了17.65%。因此,在采用移去恢复法情况下,考虑似大地水准面趋势变化的选点方案能够显著地提升高程异常拟合精度。

(4)由方案1#与方案2#、方案3#与方案4#实验结果对比表明：移去恢复法能够有效地提升高程异常曲面拟合精度,其中方案2#比方案1#拟合精度提升32.00%,方案4#比方案3#拟合精度提升44.00%。

4 结束语

基于SGG-UGM-2全球重力场模型,结合移去恢复拟合法,本文提出了一种顾及似大地水准面趋势变化的高程异常拟合方法。在对陌生测区无任何高程先验知识的情况下,此方法能够相对准确地判断出测区高程异常曲面拟合中关键已知点信息,从而减小曲面拟合过程中的精度损失。通过实例验证,本文提出的高程异常曲面拟合方法最大残差值为0.027 m,最小残差值为0.000 m,中误差为±0.014 m,其完全能够使实验区的GNSS高程测量替代四等水准方法。